Skip to main content
Global

16.3: Movimento harmônico simples - um movimento periódico especial

  1. Last updated
  2. Save as PDF
  • Page ID
    194458

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva um oscilador harmônico simples.
    • Explique a ligação entre o movimento harmônico simples e as ondas.

    As oscilações de um sistema no qual a força líquida pode ser descrita pela lei de Hooke são de especial importância, porque são muito comuns. Eles também são os sistemas oscilatórios mais simples. Movimento Harmônico Simples (SHM) é o nome dado ao movimento oscilatório para um sistema em que a força líquida pode ser descrita pela lei de Hooke, e esse sistema é chamado de oscilador harmônico simples. Se a força líquida puder ser descrita pela lei de Hooke e não houver amortecimento (por atrito ou outras forças não conservadoras), um oscilador harmônico simples oscilará com igual deslocamento em ambos os lados da posição de equilíbrio, conforme mostrado para um objeto em uma mola na Figura\(\PageIndex{1}\). O deslocamento máximo do equilíbrio é chamado de amplitude\(X\). As unidades de amplitude e deslocamento são as mesmas, mas dependem do tipo de oscilação. Para o objeto na mola, as unidades de amplitude e deslocamento são metros; enquanto que para oscilações sonoras, elas têm unidades de pressão (e outros tipos de oscilações têm ainda outras unidades). Como a amplitude é o deslocamento máximo, ela está relacionada à energia na oscilação.

    EXPERIÊNCIA PARA LEVAR PARA CASA: SHM E O MÁRMORE

    Encontre uma tigela ou bacia com a forma de um hemisfério no interior. Coloque uma bola de gude dentro da tigela e incline a tigela periodicamente para que ela role do fundo da tigela para pontos igualmente altos nas laterais da tigela. Sinta a força necessária para manter esse movimento periódico. Qual é a força restauradora e qual o papel que a força aplicada desempenha no movimento harmônico simples (SHM) do mármore?

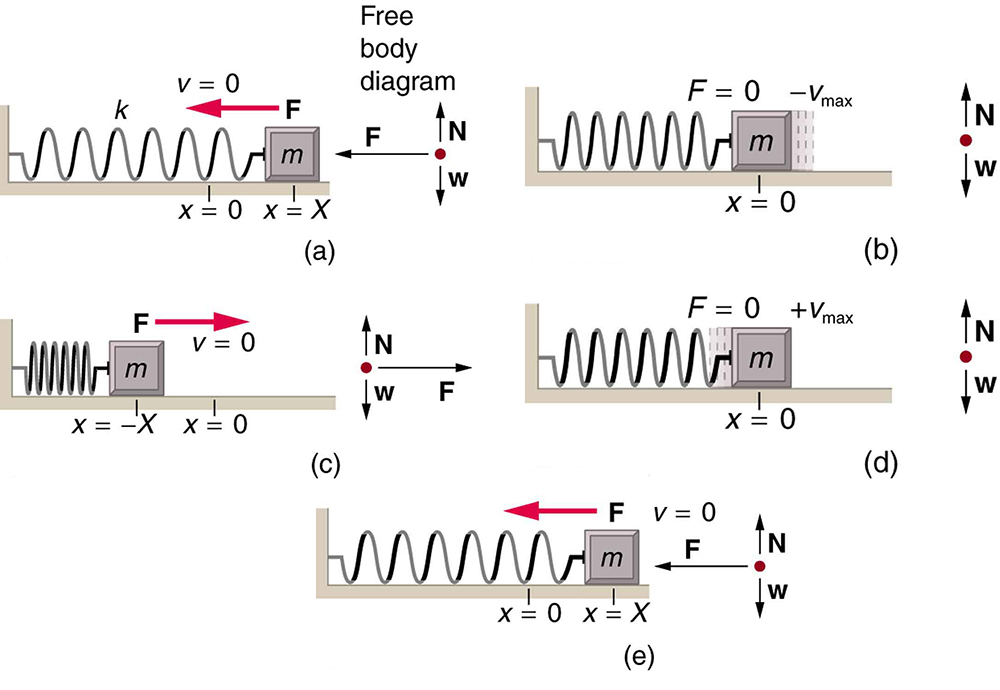
    A figura a mostra uma mola em uma superfície sem atrito presa a uma barra ou parede do lado esquerdo. No lado direito da mola, um objeto preso a ela com massa m, sua amplitude é dada por X e X é igual a zero no nível de equilíbrio. A força F é aplicada a ela do lado direito, mostrada com a seta vermelha apontada para a esquerda e a velocidade v é igual a zero. Um ponto de direção mostrando a direção norte e oeste também é fornecido ao lado desta figura, bem como com outras quatro figuras. Na figura b, após a aplicação da força, o objeto se move para a esquerda comprimindo um pouco a mola. E a área deslocada do objeto a partir de seu ponto inicial é mostrada em pontos esboçados. O F aqui é igual a zero e o v é máximo na direção negativa. Na figura c, a mola foi comprimida até o nível máximo e a amplitude é negativa X. Agora, a direção da força muda para a direção direita, mostrada com a seta vermelha apontada para a direita e a velocidade v é zero. Na figura d, a mola é mostrada liberada do nível comprimido e o objeto se moveu para o lado direito até o nível de equilíbrio. O F é zero e a velocidade v é máxima. Na figura e, a mola foi esticada até o nível máximo e o objeto foi movido para a extrema direita. Agora, novamente, a velocidade aqui é igual a zero e a direção da força novamente está para o lado esquerdo, mostrada aqui como F é igual a zero.
    Figura\(\PageIndex{1}\): Um objeto preso a uma mola deslizando em uma superfície sem atrito é um oscilador harmônico simples e simples. Quando deslocado do equilíbrio, o objeto executa um movimento harmônico simples que tem uma amplitude\(X\) e um período\(T\). A velocidade máxima do objeto ocorre quando ele passa pelo equilíbrio. Quanto mais rígida for a mola, menor será o período\(T\). Quanto maior for a massa do objeto, maior será o período\(T\).

    O que há de tão significativo no movimento harmônico simples? Uma coisa especial é que o período\(T\) e a frequência\(f\) de um oscilador harmônico simples são independentes da amplitude. A corda de uma guitarra, por exemplo, oscilará com a mesma frequência, seja puxada suavemente ou com força. Como o período é constante, um oscilador harmônico simples pode ser usado como relógio.

    Dois fatores importantes afetam o período de um oscilador harmônico simples. O período está relacionado à rigidez do sistema. Um objeto muito rígido tem uma grande constante de força\(k\), o que faz com que o sistema tenha um período menor. Por exemplo, você pode ajustar a rigidez de uma prancha de mergulho: quanto mais rígida ela for, mais rápido ela vibra e menor será o período. O período também depende da massa do sistema oscilante. Quanto mais massivo for o sistema, maior será o período. Por exemplo, uma pessoa pesada em uma prancha de mergulho salta para cima e para baixo mais lentamente do que uma pessoa leve.

    De fato, a massa\(m\) e a força constante\(k\) são os únicos fatores que afetam o período e a frequência do movimento harmônico simples.

    Período do oscilador harmônico simples

    O período de um oscilador harmônico simples é dado por

    \[T = 2\pi \sqrt{\dfrac{m}{k}}\]

    e, porque\(f = 1/T\), a frequência de um oscilador harmônico simples é

    \[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}}.\]

    Note que\(T\) nem\(f\) tem qualquer dependência da amplitude.

    EXPERIÊNCIA PARA LEVAR PARA CASA: OSCILAÇÕES DE MASSA E RÉGUA

    Encontre duas réguas idênticas de madeira ou plástico. Prenda uma extremidade de cada régua firmemente na borda de uma mesa para que o comprimento de cada régua que se projeta da mesa seja o mesmo. Na extremidade livre de uma régua, cole um objeto pesado, como algumas moedas grandes. Arranca as pontas das réguas ao mesmo tempo e observe qual delas passa por mais ciclos em um período de tempo e meça o período de oscilação de cada uma das réguas.

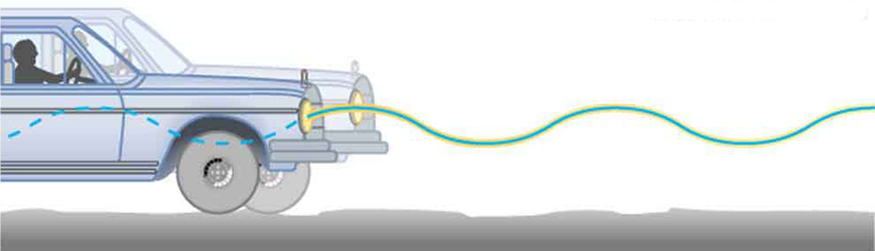
    Exemplo\(\PageIndex{1}\): Calculate the Frequency and Period of Oscillations: Bad Shock Absorbers in a Car

    Se os amortecedores de um carro ficarem ruins, o carro oscilará com o mínimo de provocação, como ao passar por cima de solavancos na estrada e depois de parar (veja a Figura\(\PageIndex{2}\)). Calcule a frequência e o período dessas oscilações para um carro desse tipo se a massa do carro (incluindo sua carga) for de 900 kg e a força constante\(k\) do sistema de suspensão for\(6.53 \times 10^4 \, N/m\).

    Estratégia

    A frequência das oscilações do carro será a de um oscilador harmônico simples, conforme indicado na equação\(f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}}\).

    A massa e a constante de força são dadas.

    Solução

    1. Insira os valores conhecidos de k e m:\[f = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}} = \dfrac{1}{2\pi} \sqrt{\dfrac{6.53 \times 10^4 \, N/m}{900 \, kg}}. \nonumber\]
    2. Calcule a frequência:\[\dfrac{1}{2\pi} \sqrt{72.6/s^{-2}} = 1.3656/s^{-1} \approx 1.36/s^{-1} = 1.36 \, Hz\nonumber\]
    3. Você poderia usar\(T = 2\pi \sqrt{\dfrac{m}{k}}\) para calcular o período, mas é mais simples usar a relação\(T = 1/f\) e substituir o valor encontrado por\(f\):\[T = \dfrac{1}{f} = \dfrac{1}{1.356 \, Hz} = 0.738 \, s.\nonumber\]

    Discussão

    Os valores de\(T\) e\(f\) ambos parecem adequados para um carro pulando. Você pode observar essas oscilações se pressionar com força a extremidade de um carro e soltá-la.

    A ligação entre movimento harmônico simples e ondas

    Se uma fotografia de exposição ao tempo do carro pulando fosse tirada enquanto ele passava, o farol faria uma faixa ondulada, conforme mostrado na Figura\(\PageIndex{2}\). Da mesma forma, a Figura\(\PageIndex{3}\) mostra um objeto saltando sobre uma mola ao deixar um “traço ondulado” de sua posição em uma tira de papel em movimento. Ambas as ondas são funções senoidais. Todo movimento harmônico simples está intimamente relacionado às ondas senoidais e cossenoidais.

    A figura mostra o lado dianteiro direito de um carro correndo em uma superfície irregular e áspera, que também mostra o motorista no banco do motorista. Há uma onda senoidal oscilante desenhada da esquerda para a direita horizontalmente em toda a figura.
    Figura\(\PageIndex{2}\): O carro saltitante faz um movimento ondulatório. Se a força de restauração no sistema de suspensão só puder ser descrita pela lei de Hooke, a onda é uma função senoidal. (A onda é o traço produzido pelo farol quando o carro se move para a direita.)
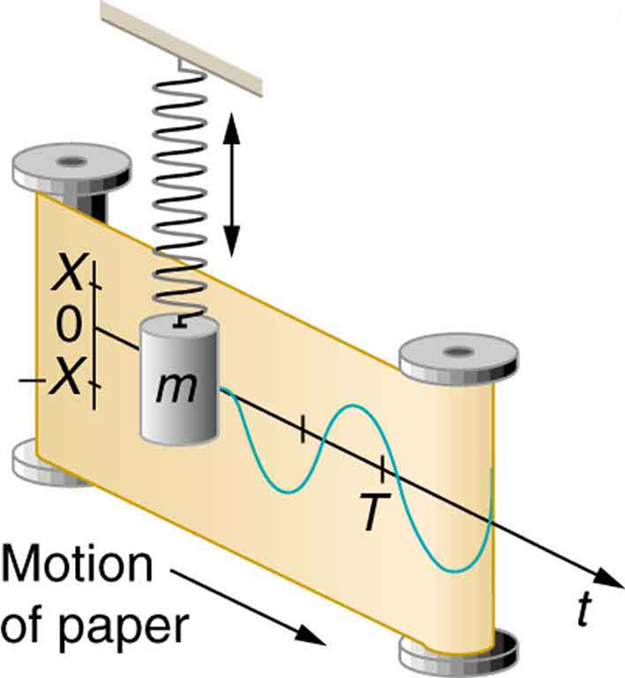
    Existem duas barras de rolo de papel de ferro posicionadas verticalmente com uma tira de papel costurada de uma barra à outra. Há uma mola suspensa vertical logo acima do meio das duas barras, perpendicular à tira do papel, com um objeto com massa m amarrado a ela. Há um gráfico de linhas com escala de amplitude como X, zero e X negativo no lado esquerdo da tira de papel, verticalmente um sobre o outro com seus pontos marcados. Uma linha perpendicular é traçada através dessa escala de amplitude para a direita com um ponto T marcado sobre ela, mostrando o tempo de duração da amplitude. Essa linha tem uma onda oscilante traçada através dela.
    Figura\(\PageIndex{3}\): A posição vertical de um objeto saltando sobre uma mola é registrada em uma tira de papel em movimento, deixando uma onda senoidal.

    O deslocamento em função do tempo\(t\) em qualquer movimento harmônico simples - ou seja, aquele em que a força restauradora líquida pode ser descrita pela lei de Hooke, é dado por

    \[x(t) = X \, cos \dfrac{2\pi t}{T},\]

    onde\(X\) está a amplitude. Em\(T = 0\), a posição inicial é\(x_0 = X\), e o deslocamento oscila para frente e para trás com um ponto \(T\). (Quando\(t = T\),\(x = X\) voltamos porque\(cos \, 2\pi = 1\)). Além disso, a partir dessa expressão para\(x\), a velocidade\(v\) em função do tempo é dada por:

    \[v(t) = -v_{max}sin \left(\dfrac{2\pi t}{T}\right),\]

    onde\(v_{max} = 2\pi X/T = X \sqrt{k/m}\). O objeto tem velocidade zero no deslocamento máximo — por exemplo\(t = 0\),\(v = 0\) quando e naquele momento\(x = X\). O sinal de menos na primeira equação para\(v(t)\) fornece a direção correta para a velocidade. Logo após o início do movimento, por exemplo, a velocidade é negativa porque o sistema está voltando para o ponto de equilíbrio. Finalmente, podemos obter uma expressão para aceleração usando a segunda lei de Newton. [Então temos\(x(t), \, v(t), \, t,\) e\(a(t)\), as quantidades necessárias para a cinemática e uma descrição do movimento harmônico simples.] De acordo com a segunda lei de Newton, a aceleração é\(a = F/m = kx/m\). Então, também\(a(t)\) é uma função de cosseno:

    \[a(t) = -\dfrac{kX}{m}cos \dfrac{2\pi t}{T}.\]

    Portanto,\(a(t)\) é diretamente proporcional e na direção oposta\(x(t)\) a. A figura\(\PageIndex{4}\) mostra o movimento harmônico simples de um objeto em uma mola e apresenta gráficos de\(x(t)\)\(v(t)\), e\(a(t)\) versus tempo.

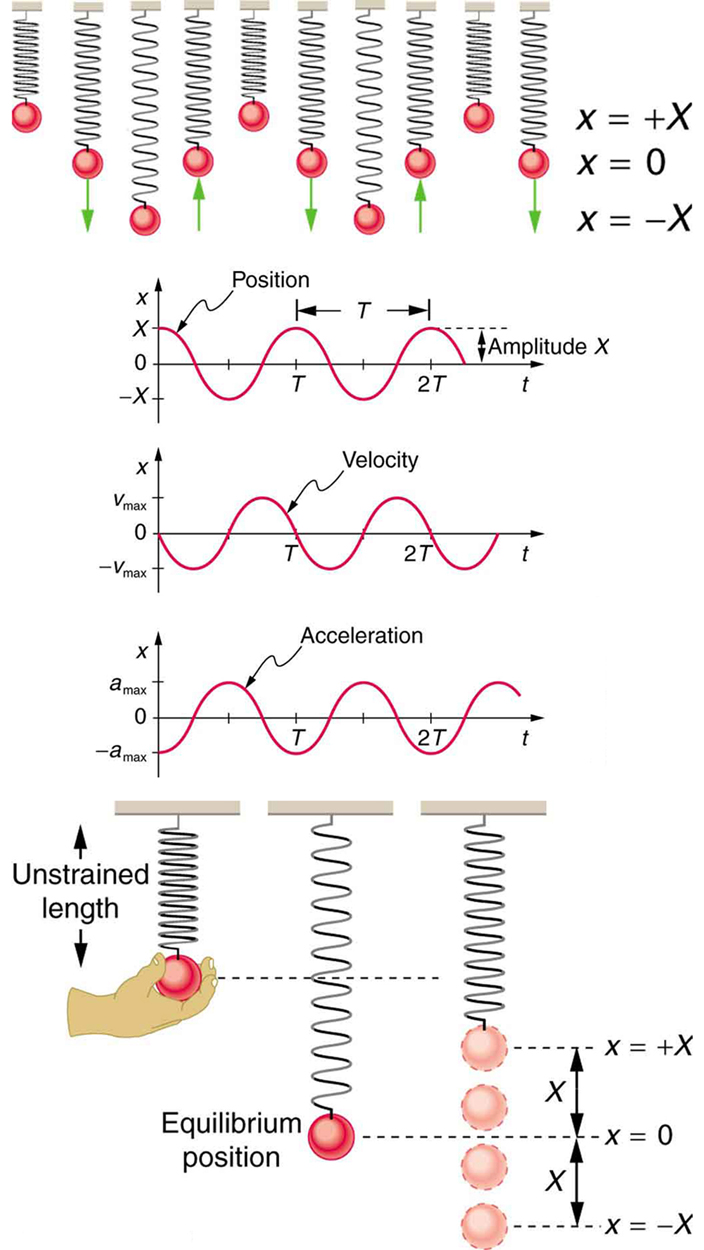
    Na figura no topo, há dez trampolins com objetos de diferentes valores de massa amarrados a eles. Isso faz com que algumas molas sejam altamente comprimidas, algumas como frouxamente esticadas e outras em equilíbrio, que são mostradas em forma esférica vermelha. Ao lado da figura, há uma escala dada para diferentes valores de amplitude como x igual a X positivo, zero e X negativo. As setas apontando para cima e para baixo são mostradas com alguns trampolins. Na segunda figura, há três gráficos. O primeiro gráfico mostra a distância percorrida na forma de uma onda senoidal a partir de um ponto x unidades no eixo y positivo. A altura da onda acima do eixo x é marcada como amplitude. A diferença entre duas cristas consecutivas é marcada como T. Abaixo do primeiro gráfico, há outro gráfico mostrando a velocidade na forma de uma onda senoidal começando da origem para baixo. No terceiro gráfico abaixo do segundo, a aceleração é mostrada na forma de onda senoidal a partir de unidades x no eixo y negativo para cima. Na última figura, três posições de uma mola são mostradas. A primeira posição mostra o comprimento não esticado de um pêndulo de mola. Uma mão está segurando a protuberância do pêndulo. Na segunda posição, a posição de equilíbrio da mola e do bob é mostrada. Essa posição é menor que a primeira. No terceiro caso, as oscilações para cima e para baixo do pêndulo da mola são mostradas. O bob está movendo x unidades nas direções ascendente e descendente, alternativamente.
    Figura\(\PageIndex{4}\): Gráficos de\(x(t), \, v(t)\) e\(a(t)\) versus\(t\) para o movimento de um objeto em uma mola. A força líquida sobre o objeto pode ser descrita pela lei de Hooke e, portanto, o objeto sofre um movimento harmônico simples. Observe que a posição inicial tem o deslocamento vertical em seu valor máximo\(X\);\(v\) é inicialmente zero e depois negativa à medida que o objeto se move para baixo; e a aceleração inicial é negativa, volta para a posição de equilíbrio e se torna zero nesse ponto.

    O ponto mais importante aqui é que essas equações são matematicamente simples e válidas para todos os movimentos harmônicos simples. Eles são muito úteis na visualização de ondas associadas a movimentos harmônicos simples, incluindo a visualização de como as ondas se somam umas às outras.

    Exercício\(\PageIndex{1}\)

    Suponha que você puxe uma corda de banjo. Você ouve uma única nota que começa em voz alta e se acalma lentamente com o tempo. Descreva o que acontece com as ondas sonoras em termos de período, frequência e amplitude à medida que o volume do som diminui.

    Resposta

    A frequência e o período permanecem essencialmente inalterados. Somente a amplitude diminui à medida que o volume diminui.

    Exercício\(\PageIndex{2}\)

    Uma babá está empurrando uma criança em um balanço. No ponto em que a oscilação chega\(x\), onde estaria localizado o ponto correspondente em uma onda desse movimento?

    Resposta

    \(x\)é a deformação máxima, que corresponde à amplitude da onda. O ponto na onda estaria na parte superior ou na parte inferior da curva.

    EXPLORAÇÕES DE PHET: MASSAS E CORDAS

    Um laboratório realista de massas e molas. Pendure massas nas molas e ajuste a rigidez e o amortecimento da mola. Você pode até mesmo diminuir o tempo. Transporte o laboratório para diferentes planetas. Um gráfico mostra a energia cinética, potencial e térmica de cada primavera.

    Figura\(\PageIndex{5}\): Massas e Molas

    Resumo

    • O movimento harmônico simples é o movimento oscilatório de um sistema que só pode ser descrito pela lei de Hooke. Esse sistema também é chamado de oscilador harmônico simples.
    • O deslocamento máximo é a amplitude\(X\). O período\(T\) e a frequência\(f\) de um oscilador harmônico simples são dados por\(T = 2\pi \sqrt{\frac{m}{k}}\) e\(f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}\), onde\(m\) está a massa do sistema.
    • O deslocamento em movimento harmônico simples em função do tempo é dado por\(x = X \, cos \, \frac{2\pi t}{T}\).
    • A velocidade é dada por\(v(t) = -v_{max}sin \frac{2\pi t}{T}\), onde\(v_{max} = \sqrt{k/m}X\).
    • Descobriu-se que a aceleração é\(a = -\frac{kX}{m} \, cos \frac{2\pi t}{T}\).

    Glossário

    amplitude
    o deslocamento máximo da posição de equilíbrio de um objeto oscilando em torno da posição de equilíbrio
    movimento harmônico simples
    o movimento oscilatório em um sistema onde a força líquida pode ser descrita pela lei de Hooke
    oscilador harmônico simples
    um dispositivo que implementa a lei de Hooke, como uma massa presa a uma mola, com a outra extremidade da mola sendo conectada a um suporte rígido, como uma parede