11.4: Variação da pressão com a profundidade em um fluido
- Page ID
- 195211
Objetivos de
Ao final desta seção, você poderá:
- Defina a pressão em termos de peso.
- Explique a variação da pressão com a profundidade em um fluido.
- Calcule a densidade dada a pressão e a altitude.
Se seus ouvidos já estouraram em um voo de avião ou doeram durante um mergulho profundo em uma piscina, você experimentou o efeito da profundidade na pressão de um fluido. Na superfície da Terra, a pressão do ar exercida sobre você é resultado do peso do ar acima de você. Essa pressão é reduzida à medida que você sobe em altitude e o peso do ar acima de você diminui. Sob a água, a pressão exercida sobre você aumenta com o aumento da profundidade. Nesse caso, a pressão exercida sobre você é resultado tanto do peso da água acima de você quanto da atmosfera acima de você. Você pode notar uma mudança na pressão do ar em um passeio de elevador que transporta muitas histórias, mas você só precisa mergulhar cerca de um metro abaixo da superfície de uma piscina para sentir um aumento de pressão. A diferença é que a água é muito mais densa que o ar, cerca de 775 vezes mais densa.
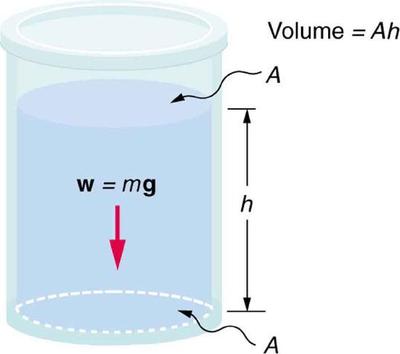
Considere o contêiner na Figura\(\PageIndex{1}\). Seu fundo suporta o peso do fluido nele. Vamos calcular a pressão exercida na parte inferior pelo peso do fluido. Essa pressão é o peso do fluido\(mg\) dividido pela área que o\(A\) sustenta (a área do fundo do recipiente):
\[P = \dfrac{mg}{A}.\]
Podemos encontrar a massa do fluido a partir de seu volume e densidade:
\[m = \rho V.\]
O volume do fluido\(V\) está relacionado às dimensões do recipiente. É
\[V = Ah,\]
onde\(A\) está a área da seção transversal e\(h\) é a profundidade. A combinação das duas últimas equações dá\[m = \rho Ah.\]
Se inserirmos isso na expressão de pressão, obtemos\[P = \dfrac{(\rho Ah)g}{A}.\]
A área é cancelada e a reorganização das variáveis gera
\[P = h\rho g. \label{eq10}\]
Esse valor é a pressão devida ao peso de um fluido. A equação\ ref {eq10} tem validade geral além das condições especiais sob as quais ela é derivada aqui. Mesmo que o recipiente não estivesse lá, o fluido circundante ainda exerceria essa pressão, mantendo o fluido estático. Assim, a Equação\ ref {eq10} representa a pressão devida ao peso de qualquer fluido de densidade média\(\rho\) em qualquer profundidade\(h\) abaixo de sua superfície. Para líquidos, que são quase incompressíveis, essa equação se mantém em grandes profundidades. Para gases, que são bastante compressíveis, pode-se aplicar essa equação desde que as mudanças de densidade sejam pequenas acima da profundidade considerada. O exemplo\(\PageIndex{1}\) ilustra essa situação.
Exemplo\(\PageIndex{1}\): Calculating the Average Pressure and Force Exerted: What Force Must a Dam Withstand?
Em [link], calculamos a massa de água em um grande reservatório. Agora, consideraremos a pressão e a força atuando na barragem que retém a água (Figura\(\PageIndex{2}\)). A barragem tem 500 m de largura e a água tem 80,0 m de profundidade na barragem.
- Qual é a pressão média na barragem devido à água?
- Calcule a força exercida contra a barragem e compare-a com o peso da água na barragem (anteriormente constatado ser\(1.96 \times 10^{13} \, N.\)
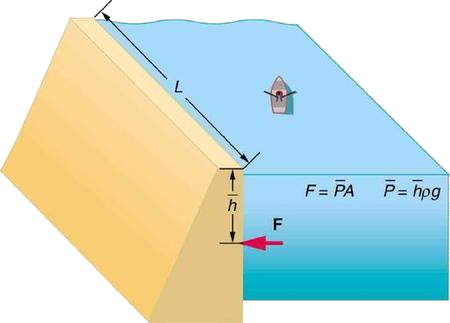
Estratégia para (a)
A pressão média\(\overline{P}\) devido ao peso da água é a pressão na profundidade média\(\overline{h}\) de 40,0 m, pois a pressão aumenta linearmente com a profundidade.
Solução para (a)
A pressão média devido ao peso de um fluido (Equação\ ref {eq10}) é
\[\overline{P} = \overline{h}\rho g. \nonumber \]
Entrando na densidade da água de [link] e considerando\(\overline{h}\) a profundidade média de 40,0 m, obtemos
\[ \begin{align*} \overline{P} &= (40.0 \, m)\left(10^3 \, \frac{kg}{m^3} \right) \left(9.80\, \frac{m}{s^2} \right) \\[5pt] &= 3.92 \times 10^5 \, \frac{N}{m^2} = 392 \, kPa. \end{align*} \]
Estratégia para (b)
A força exercida na barragem pela água é a pressão média vezes a área de contato:
\[F = \overline{P} A. \nonumber \]
Solução para (b)
Já encontramos o valor para\(\overline{P}\). A área da barragem é
\[A = 80.0 \, m \times 500 \, m = 4.00 \times 10^4 \, m^2,\nonumber\]
para que
\[ \begin{align*} F &= (3.92 \times 10^5 \, N/m^2)(4.00 \times 10^4 \, m^2) \\[5pt] &= 1.57 \times 10^{10} \, N.\end{align*} \]
Discussão
Embora essa força pareça grande, ela é pequena em comparação com o\(1.96 \times 10^{13} \, N\) peso da água no reservatório — na verdade, é apenas\(0.0800 \, \% \) do peso. Observe que a pressão encontrada na parte (a) é completamente independente da largura e do comprimento do lago — ela depende apenas de sua profundidade média na barragem. Assim, a força depende apenas da profundidade média da água e das dimensões da barragem, não da extensão horizontal do reservatório. No diagrama, a espessura da barragem aumenta com a profundidade para equilibrar a força crescente devido ao aumento da pressão.epth para equilibrar a força crescente devido ao aumento da pressão.
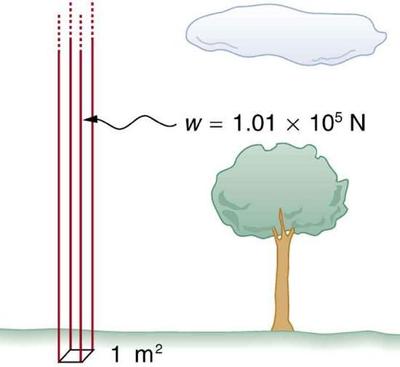
A pressão atmosférica é outro exemplo de pressão devido ao peso de um fluido, neste caso devido ao peso do ar acima de uma determinada altura. A pressão atmosférica na superfície da Terra varia um pouco devido ao fluxo da atmosfera em grande escala induzido pela rotação da Terra (isso cria “altos” e “baixos” climáticos). No entanto, a pressão média ao nível do mar é dada pela pressão atmosférica padrão\(P_{atm}\), medida em
\[1 \, atmosphere \, (atm) = P_{atm} = 1.01 \times 10^5 \, N/m^2 = 101 \, kPa.\]
Essa relação significa que, em média, ao nível do mar, uma coluna de ar acima\(1.00 \, m^2 \) da superfície da Terra tem um peso\(1.01 \times 10^5 \, N,\) equivalente a 1 atm (Figura\(\PageIndex{3}\)).
Exemplo\(\PageIndex{2}\): Calculating Average Density: How Dense Is the Air?
Calcule a densidade média da atmosfera, uma vez que ela se estende até uma altitude de 120 km. Compare essa densidade com a do ar listada em [link].
Estratégia
Se\(P = h\rho g \) resolvermos a densidade, vemos que
\[\overline{\rho} = \dfrac{P}{hg}.\nonumber\]
Em seguida, consideramos\(P\) a pressão atmosférica,\(h\) é dada e\(g\) é conhecida, e então podemos usar isso para calcular\(\overline{\rho}\).
Solução
Inserindo valores conhecidos na expressão para\(\overline{\rho}\) rendimentos
\[ \begin{align*} \overline{\rho} &= \dfrac{1.01 \times 10^5 \, N/m^2}{(120 \times 10^3 \, m)(9.80 \, m/s^2)} \\[5pt] &= 8.59 \times 10^{-2} \, kg/m^3. \end{align*} \]
Discussão
Esse resultado é a densidade média do ar entre a superfície da Terra e o topo da atmosfera terrestre, que essencialmente termina em 120 km. A densidade do ar ao nível do mar é dada em [link] como\(1.29 \, kg/m^3 \) - cerca de 15 vezes seu valor médio. Como o ar é muito compressível, sua densidade tem seu maior valor próximo à superfície da Terra e diminui rapidamente com a altitude.
Exemplo\(\PageIndex{3}\): Calculating Depth Below the Surface of Water: What Depth of Water Creates the Same Pressure as the Entire Atmosphere?
Calcule a profundidade abaixo da superfície da água na qual a pressão devido ao peso da água é igual a 1,00 atm.
Estratégia
Começamos resolvendo a equação\(P = h\rho g\) da profundidade\(h\):
\[h = \dfrac{P}{\rho g}.\nonumber\]
Em seguida,\(P\) consideramos 1,00 atm e\(\rho \)
ser a densidade da água que cria a pressão.
Solução
Inserindo os valores conhecidos na expressão para\(h\) dá
\[ \begin{align*} h &= \dfrac{1.01 \times 10^5 \, N/m^2}{(1.00 \times 10^3 \, m)(9.80 \, m/s^2)} \\[5pt] &= 10.3 \, m. \end{align*} \]
Discussão
Apenas 10,3 m de água criam a mesma pressão que 120 km de ar. Como a água é quase incompressível, podemos negligenciar qualquer alteração em sua densidade nessa profundidade.
O que você acha que é a pressão total a uma profundidade de 10,3 m em uma piscina? A pressão atmosférica na superfície da água afeta a pressão abaixo? A resposta é sim. Isso parece lógico, já que tanto o peso da água quanto o da atmosfera devem ser suportados. Portanto, a pressão total a uma profundidade de 10,3 m é de 2 atm — metade da água acima e metade do ar acima. Veremos no Princípio de Pascal que as pressões dos fluidos sempre aumentam dessa maneira.
Resumo
- Pressão é o peso do fluido\(mg\) dividido pela área que o\(A\) sustenta (a área do fundo do recipiente):\[P = \dfrac{mg}{A}. \nonumber\]
- A pressão devida ao peso de um líquido é dada por\[P = h\rho g, \nonumber\] onde\(P\)\(h\) está a pressão, é a altura do líquido,\(\rho\) é a densidade do líquido e\(g\) é a aceleração devido à gravidade.
Glossário
- pressão
- o peso do fluido dividido pela área que o sustenta


