11.5: Princípio de Pascal

Objetivos de

Ao final desta seção, você poderá:

• Defina pressão.
• Declare o princípio de Pascal.
• Entenda as aplicações do princípio de Pascal.
• Determine relações entre forças em um sistema hidráulico.

A pressão é definida como força por unidade de área. A pressão pode ser aumentada em um fluido empurrando-o diretamente sobre o fluido? Sim, mas é muito mais fácil se o fluido estiver fechado. O coração, por exemplo, aumenta a pressão arterial ao pressionar diretamente o sangue em um sistema fechado (válvulas fechadas em uma câmara). Se você tentar empurrar um fluido em um sistema aberto, como um rio, o fluido flui para longe. Um fluido fechado não pode fluir para longe e, portanto, a pressão é aumentada mais facilmente por uma força aplicada.

O que acontece com a pressão em um fluido fechado? Como os átomos em um fluido podem se mover livremente, eles transmitem a pressão para todas as partes do fluido e para as paredes do recipiente. Surpreendentemente, a pressão é transmitida sem diminuição. Esse fenômeno é chamado de princípio de Pascal, porque foi afirmado claramente pela primeira vez pelo filósofo e cientista francês Blaise Pascal (1623—1662): Uma mudança na pressão aplicada a um fluido fechado é transmitida sem diminuir para todas as partes do fluido e para as paredes de seu recipiente.

Definição: Princípio de Pascal

Uma mudança na pressão aplicada a um fluido fechado é transmitida sem diminuir para todas as partes do fluido e para as paredes de seu recipiente.

O princípio de Pascal, um fato verificado experimentalmente, é o que torna a pressão tão importante em fluidos. Como uma mudança na pressão é transmitida sem diminuição em um fluido fechado, geralmente sabemos mais sobre pressão do que outras quantidades físicas em fluidos. Além disso, o princípio de Pascal implica que a pressão total em um fluido é a soma das pressões de diferentes fontes. Acharemos esse fato — que as pressões acrescentam — muito útil.

Blaise Pascal teve uma vida interessante, pois foi educado em casa por seu pai, que removeu todos os livros didáticos de matemática de sua casa e o proibiu de estudar matemática até os 15 anos. Isso, é claro, despertou a curiosidade do garoto e, aos 12 anos, ele começou a aprender geometria sozinho. Apesar dessa privação precoce, Pascal passou a fazer grandes contribuições nos campos matemáticos da teoria da probabilidade, teoria dos números e geometria. Ele também é conhecido por ser o inventor da primeira calculadora digital mecânica, além de suas contribuições no campo da estática de fluidos.

Aplicação do Princípio de Pascal

Uma das aplicações tecnológicas mais importantes do princípio de Pascal é encontrada em um sistema hidráulico, que é um sistema de fluido fechado usado para exercer forças. Os sistemas hidráulicos mais comuns são aqueles que operam freios de automóveis. Vamos primeiro considerar o sistema hidráulico simples mostrado na Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Um sistema hidráulico típico com dois cilindros cheios de fluido, tampados com pistões e conectados por um tubo chamado linha hidráulica. Uma força descendente\(F_1\) no pistão esquerdo cria uma pressão que é transmitida sem diminuir para todas as partes do fluido fechado. Isso resulta em uma força ascendente\(F_2\) no pistão direito que é maior do que\(F_1\) porque o pistão direito tem uma área maior.

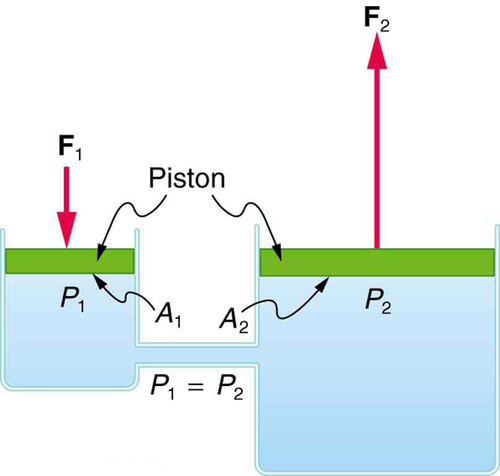
Relação entre forças em um sistema hidráulico

Podemos derivar uma relação entre as forças no sistema hidráulico simples mostrado na Figura\(\PageIndex{1}\) aplicando o princípio de Pascal. Observe primeiro que os dois pistões do sistema estão na mesma altura e, portanto, não haverá diferença na pressão devido a uma diferença na profundidade. Agora, a pressão devido à\(F_1\) atuação na área\(A_1\) é simples\(P_1 = \frac{F_1}{A_1}\), conforme definido por\(P = \frac{F}{A}\). De acordo com o princípio de Pascal, essa pressão é transmitida sem diminuir por todo o fluido e para todas as paredes do recipiente. Assim, uma pressão\(P_2\) é sentida no outro pistão que é igual\(P_1\) a. Isso é

\[P_1 = P_2\]

Mas desde então\(P_2 - \frac{F_2}{A_2}\), vemos que

\[\dfrac{F_1}{A_1} = \frac{F_2}{A_2}. \label{eq20}\]

Essa equação relaciona as relações entre força e área em qualquer sistema hidráulico, desde que os pistões estejam na mesma altura vertical e que o atrito no sistema seja insignificante. Os sistemas hidráulicos podem aumentar ou diminuir a força aplicada a eles. Para aumentar a força, a pressão é aplicada em uma área maior. Por exemplo, se uma força de 100-N for aplicada ao cilindro esquerdo na Figura\(\PageIndex{1}\) e a direita tiver uma área cinco vezes maior, a força de saída será de 500 N. Os sistemas hidráulicos são análogos às alavancas simples, mas têm a vantagem de que a pressão pode ser enviada através de linhas tortuosamente curvas para várias lugares ao mesmo tempo.

Exemplo\(\PageIndex{1}\): Calculating Force of Slave Cylinders: Pascal Puts on the Brakes

Considere o sistema hidráulico do automóvel mostrado na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Os freios hidráulicos usam o princípio de Pascal. O motorista exerce uma força de 100 N no pedal do freio. Essa força é aumentada pela alavanca simples e novamente pelo sistema hidráulico. Cada um dos cilindros escravos idênticos recebe a mesma pressão e, portanto, cria a mesma saída de força\(F_2\). As áreas circulares da seção transversal dos cilindros mestre e escravo são representadas por\(A_1\) e\(A_2\), respectivamente

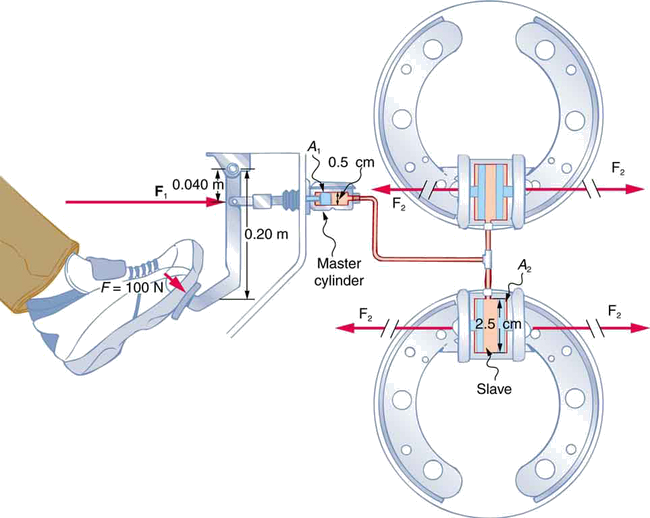
Uma força de 100 N é aplicada ao pedal do freio, que atua no cilindro — chamado de mestre — por meio de uma alavanca. Uma força de 500 N é exercida no cilindro mestre. (O leitor pode verificar se a força é de 500 N usando técnicas de estática de Aplicações da Estática, incluindo estratégias de resolução de problemas.) A pressão criada no cilindro mestre é transmitida para os quatro chamados cilindros escravos. O cilindro mestre tem um diâmetro de 0,500 cm e cada cilindro escravo tem um diâmetro de 2,50 cm. Calcule a força\(F_2\) criada em cada um dos cilindros escravos.

Estratégia

Recebemos\(F_1\) a força aplicada ao cilindro mestre. As áreas\(A_1\) da seção transversal\(A_2\) podem ser calculadas a partir de seus diâmetros fornecidos. Então a Equação\ ref {eq20} pode ser usada para encontrar a força\(F_2\). Manipule isso algebricamente para obter\(F_2\)

de um lado e substitua os valores conhecidos:

Solução

O princípio de Pascal aplicado aos sistemas hidráulicos é dado pela Equação\ ref {eq20}:

\[\begin{align*} F_2 &= \dfrac{A_2}{A_1}F_1 \\[5pt] &= \dfrac{\pi r_2^2}{\pi r_1^2}F_1 \\[5pt] &= \dfrac{(1.25 \, cm)^2}{(0.250 \, cm)^2} \times 500 \, N \\[5pt] &= 1.25 \times 10^4 \, N. \end{align*} \]

Discussão

Esse valor é a força exercida por cada um dos quatro cilindros escravos. Note que podemos adicionar quantos cilindros escravos quisermos. Se cada um tiver um diâmetro de 2,50 cm, cada um exercerá\(1.25 \times 10^4 \, N.\)

Um sistema hidráulico simples, como uma máquina simples, pode aumentar a força, mas não pode fazer mais trabalho do que fazer nele. O trabalho é a força vezes a distância percorrida e o cilindro escravo se move por uma distância menor do que o cilindro mestre. Além disso, quanto mais escravos forem adicionados, menor será a distância que cada um se move. Muitos sistemas hidráulicos, como freios elétricos e aqueles em escavadeiras, têm uma bomba motorizada que realmente faz a maior parte do trabalho no sistema. O movimento das pernas de uma aranha é realizado em parte pela hidráulica. Usando a hidráulica, uma aranha saltadora pode criar uma força que a torna capaz de pular 25 vezes seu comprimento!

Definição: Conservação de energia

A conservação da energia aplicada a um sistema hidráulico nos diz que o sistema não pode trabalhar mais do que nele. O trabalho transfere energia e, portanto, a saída de trabalho não pode exceder a entrada de trabalho. Freios elétricos e outros sistemas hidráulicos similares usam bombas para fornecer energia extra quando necessário.

Resumo

• Pressão é força por unidade de área.
• Uma mudança na pressão aplicada a um fluido fechado é transmitida sem diminuir para todas as partes do fluido e para as paredes de seu recipiente.
• Um sistema hidráulico é um sistema de fluido fechado usado para exercer forças.

Glossário

Princípio de Pascal

uma mudança na pressão aplicada a um fluido fechado é transmitida sem diminuir para todas as partes do fluido e para as paredes de seu recipiente