11.3: Pressão
- Page ID
- 195235
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Defina pressão.
- Explique a relação entre pressão e força.
- Calcule a força dada a pressão e a área.
Sem dúvida, você já ouviu a palavra pressão sendo usada em relação ao sangue (pressão alta ou baixa) e em relação ao clima (sistemas climáticos de alta e baixa pressão). Esses são apenas dois dos muitos exemplos de pressões em fluidos.
Definição: Pressão
A pressão é definida como a força dividida pela área perpendicular à força sobre a qual a força é aplicada, ou
\[P = \dfrac{F}{A}. \label{pressure}\]
onde\(F\) é uma força aplicada a uma área\(A\) que é perpendicular à força.
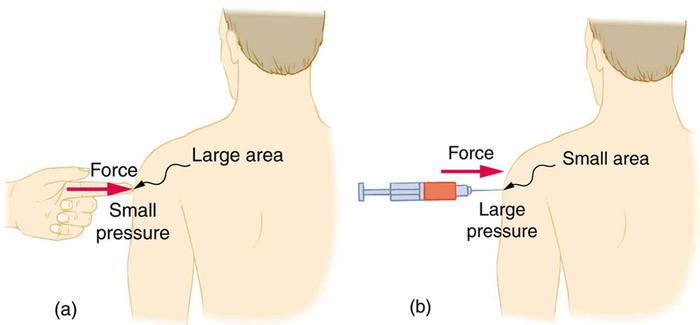
Uma determinada força pode ter um efeito significativamente diferente dependendo da área sobre a qual a força é exercida, conforme mostrado na Figura Figura\(\PageIndex{1}\). A unidade SI para pressão é o pascal, onde
\[1 \, Pa = 1 \, N/m^2.\]
Além do pascal, existem muitas outras unidades de pressão que são de uso comum. Em meteorologia, a pressão atmosférica é frequentemente descrita em unidades de milibar (mb), onde
\[100 \, mb = 1 \times 10^4 \, Pa.\]
Às vezes, libras por\((lb/in^2 \, or \, psi)\) polegada quadrada ainda são usadas como medida da pressão dos pneus, e milímetros de mercúrio (mm Hg) ainda são frequentemente usados na medição da pressão arterial. A pressão é definida para todos os estados da matéria, mas é particularmente importante ao discutir fluidos.
Exemplo\(\PageIndex{1}\): Calculating Force Exerted by the Air - What Force Does a Pressure Exert?
Um astronauta está trabalhando fora da Estação Espacial Internacional, onde a pressão atmosférica é essencialmente zero. O medidor de pressão em seu tanque de ar diz\(6.9 \times 10^6 \, Pa\). Que força o ar dentro do tanque exerce na extremidade plana do tanque cilíndrico, um disco de 0,150 m de diâmetro?
Estratégia
Podemos encontrar a força exercida a partir da definição de pressão (Equação\ red {pressão}), desde que possamos encontrar a área sobre a qual\(A\) atua.
Solução
Ao reorganizar a definição de pressão (Equação\ red {pressão}) para resolver a força, vemos que
\[F = PA.\nonumber\]
Aqui, a pressão\(P\) é dada, assim como a área da extremidade do cilindro\(A\), dada por\(A = \pi r^2\). Assim
\[ \begin{align*} F &= (6.90 \times 10^6 \, Pa)(3.14)(0.0750 \, m)^2 \\[5pt] &= 1.22 \times 10^5 \, N. \end{align*}\]
Discussão
Uau! Não é de admirar que o tanque deva ser forte. Como descobrimos\(F = PA\), vemos que a força exercida por uma pressão é diretamente proporcional à área sobre a qual atuamos, bem como à própria pressão.
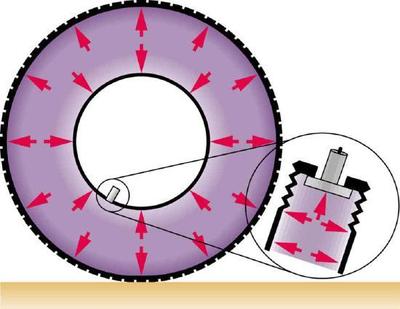
A força exercida na extremidade do tanque é perpendicular à sua superfície interna. Essa direção ocorre porque a força é exercida por um fluido estático ou estacionário. Já vimos que os fluidos não podem suportar forças de cisalhamento (laterais); eles também não podem exercer forças de cisalhamento. A pressão do fluido não tem direção, sendo uma quantidade escalar. As forças devidas à pressão têm direções bem definidas: elas são sempre exercidas perpendicularmente a qualquer superfície. (Veja o pneu na Figura\(\PageIndex{2}\), por exemplo.)
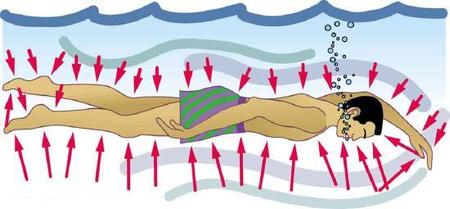
Finalmente, observe que a pressão é exercida em todas as superfícies. Os nadadores, assim como o pneu, sentem pressão em todos os lados (Figura\(\PageIndex{3}\)).
EXPLORAÇÕES DE PHET: PROPRIEDADES DO GÁS
Bombeie as moléculas de gás nesta simulação para uma caixa e veja o que acontece quando você altera o volume, adiciona ou remove calor, muda a gravidade e muito mais. Meça a temperatura e a pressão e descubra como as propriedades do gás variam em relação umas às outras.
Resumo
- Pressão é a força por unidade de área perpendicular sobre a qual a força é aplicada. Na forma de equação, a pressão é definida como\[F = PA. \nonumber\]
- A unidade de pressão SI é pascal e\(1 \, Pa = 1 \, N/m^2.\)
Glossário
- pressão
- a força por unidade de área perpendicular à força sobre a qual a força atua


