10.3: Dinâmica do movimento rotacional - Inércia rotacional

objetivos de aprendizagem

Ao final desta seção, você poderá:

• Entenda a relação entre força, massa e aceleração.
• Estude o efeito giratório da força.
• Estude a analogia entre força e torque, massa e momento de inércia e aceleração linear e aceleração angular.

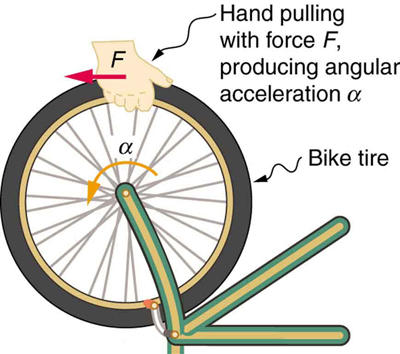
Se você já girou uma roda de bicicleta ou empurrou um carrossel, sabe que é necessária força para alterar a velocidade angular, conforme visto na Figura 10.4.1. Na verdade, sua intuição é confiável para prever muitos dos fatores envolvidos. Por exemplo, sabemos que uma porta se abre lentamente se nos aproximarmos demais de suas dobradiças. Além disso, sabemos que quanto mais grande a porta, mais lentamente ela se abre. O primeiro exemplo implica que quanto mais a força é aplicada do pivô, maior a aceleração angular; outra implicação é que a aceleração angular é inversamente proporcional à massa. Essas relações devem parecer muito semelhantes às relações familiares entre força, massa e aceleração incorporadas na segunda lei do movimento de Newton. Na verdade, existem análogos rotacionais precisos tanto da força quanto da massa.

Figura\(\PageIndex{1}\): É necessária força para girar a roda da bicicleta. Quanto maior a força, maior a aceleração angular produzida. Quanto mais massiva a roda, menor a aceleração angular. Se você pressionar um raio mais perto do eixo, a aceleração angular será menor.

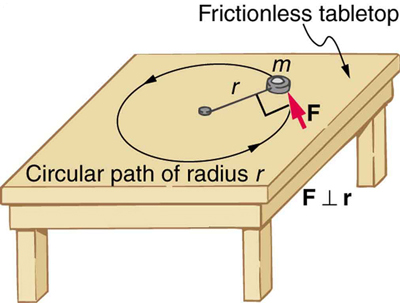
Para desenvolver a relação precisa entre força, massa, raio e aceleração angular, considere o que acontece se exercermos uma força\(F\) sobre uma massa pontual\(m\) que está a uma\(r\) distância de um ponto de articulação, conforme mostrado na Figura 10.4.2. Como a força é perpendicular a\(r\), uma aceleração\(a = frac{F}{m}\) é obtida na direção de\(F\). Podemos reorganizar essa equação de forma que\(F = ma\), em seguida, procurar maneiras de relacionar essa expressão com expressões para quantidades rotacionais. Observamos que\(a = r\alpha\), e substituímos essa expressão por\(F = ma\), produzindo\[F = mr\alpha.\] Lembre-se de que o torque é a eficácia de giro de uma força. Nesse caso, porque\(F\) é perpendicular a\(r\), o torque é simples\(\tau = Fr\). Então, se multiplicarmos os dois lados da equação acima por\(r\), obteremos torque no lado esquerdo. Ou seja,\[rF = mr^2\alpha\] ou\[\tau = mr^2\alpha.\]

Essa última equação é o análogo rotacional da segunda lei de Newton\(F = ma\), onde o torque é análogo à força, a aceleração angular é análoga à aceleração translacional e\(mr^2\) é análoga à massa (ou inércia). A quantidade\(mr^2\) é chamada de inércia rotacional ou momento de inércia de uma massa pontual a\(m\) uma\(r\) distância do centro de rotação.

Figura\(\PageIndex{2}\): Um objeto é suportado por uma mesa horizontal sem atrito e é preso a um ponto de articulação por um cabo que fornece força centrípeta. Uma força\(F\) é aplicada ao objeto perpendicular ao raio\(r\), fazendo com que ele acelere em torno do ponto de articulação. A força é mantida perpendicular\(r\) a.

Fazendo conexões: dinâmica de movimento rotacional

A dinâmica do movimento rotacional é completamente análoga à dinâmica linear ou translacional. A dinâmica se preocupa com força e massa e seus efeitos no movimento. Para o movimento rotacional, encontraremos análogos diretos à força e à massa que se comportam exatamente como esperaríamos de nossas experiências anteriores.

Inércia rotacional e momento de inércia

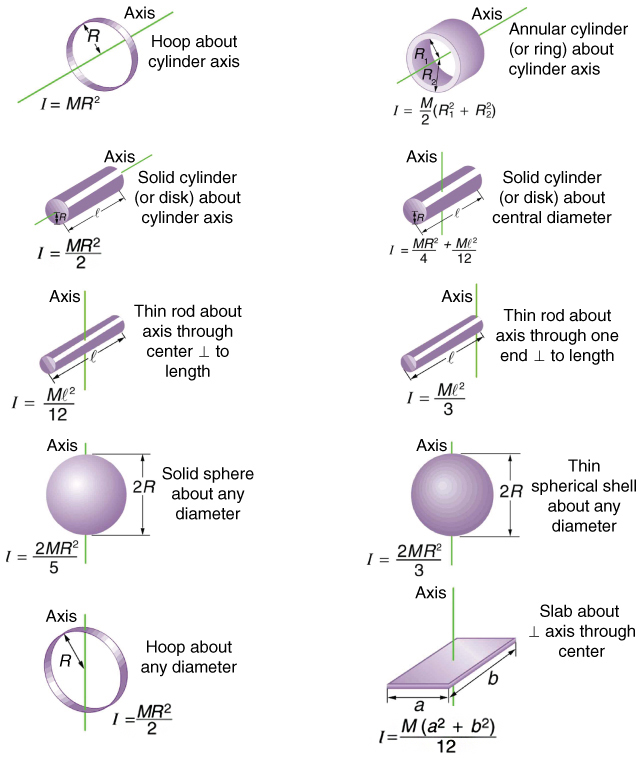
Antes de podermos considerar a rotação de qualquer coisa que não seja uma massa pontual como a da Figura, devemos estender a ideia de inércia rotacional a todos os tipos de objetos. Para expandir nosso conceito de inércia rotacional, definimos o momento de inércia\(I\) de um objeto como a soma\(mr^2\) de todas as massas pontuais das quais ele é composto. Isso é,\(I = \sum mr^2\). Aqui\(I\) é análogo ao\(m\) movimento translacional. Por causa da distância\(r\), o momento de inércia de qualquer objeto depende do eixo escolhido. Na verdade, o cálculo\(I\) está além do escopo deste texto, exceto por um caso simples: o de um arco, que tem toda a sua massa à mesma distância de seu eixo. O momento de inércia de um arco em torno de seu eixo é\(MR^2\), portanto, onde\(M\) está sua massa total e\(R\) seu raio. (Usamos\(M\) e\(R\) para um objeto inteiro para distingui-los de\(m\) e\(r\) para massas de pontos.) Em todos os outros casos, devemos consultar a Figura 10.4.3 (observe que a tabela é uma obra de arte que tem formas e fórmulas) para obter\(I\) fórmulas derivadas da integração no corpo contínuo. Observe que\(I\) tem unidades de massa multiplicadas pela distância ao quadrado\((kg \cdot m^2)\), como poderíamos esperar de sua definição.

Figura\(\PageIndex{3}\): Algumas inércias rotacionais.

A relação geral entre torque, momento de inércia e aceleração angular é\[net \, \tau = I \alpha\] ou\[\alpha = \dfrac{net \, \tau}{I},\] onde líquido\(\tau\) é o torque total de todas as forças em relação a um eixo escolhido. Para simplificar, consideraremos apenas os torques exercidos pelas forças no plano de rotação. Esses torques são positivos ou negativos e somados como números comuns. A relação em\(\tau = I\alpha\),\(\alpha = \frac{net \, \tau}{I}\) é o análogo rotacional da segunda lei de Newton e é geralmente aplicável. Essa equação é realmente válida para qualquer torque, aplicado a qualquer objeto, em relação a qualquer eixo.

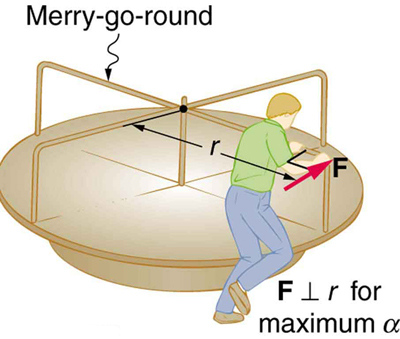
Como seria de esperar, quanto maior o torque, maior será a aceleração angular. Por exemplo, quanto mais uma criança pressiona um carrossel, mais rápido ela acelera. Além disso, quanto mais massivo for um carrossel, mais lento ele acelera com o mesmo torque. A relação básica entre o momento de inércia e a aceleração angular é que quanto maior o momento de inércia, menor é a aceleração angular. Mas há uma reviravolta adicional. O momento de inércia depende não apenas da massa de um objeto, mas também de sua distribuição de massa em relação ao eixo em torno do qual ele gira. Por exemplo, será muito mais fácil acelerar um carrossel cheio de crianças se elas ficarem perto de seu eixo do que se todas ficarem na borda externa. A massa é a mesma nos dois casos; mas o momento de inércia é muito maior quando as crianças estão no limite.

Experiência para levar para casa

• Recorte um círculo com cerca de 10 cm de raio de papelão rígido. Perto da borda do círculo, escreva os números de 1 a 12, como horas, no mostrador do relógio. Posicione o círculo de forma que ele possa girar livremente em torno de um eixo horizontal através de seu centro, como uma roda. (Você pode pregar o círculo frouxamente em uma parede.) Mantenha o círculo parado e, com o número 12 posicionado na parte superior, coloque um pedaço de massa azul (material adesivo usado para fixar pôsteres nas paredes) no número 3. Qual é o tamanho do caroço para simplesmente girar o círculo? Descreva como você pode alterar o momento de inércia do círculo. Como essa mudança afeta a quantidade de massa azul necessária no número 3 para apenas girar o círculo? Altere o momento de inércia do círculo e tente girar o círculo usando diferentes quantidades de massa azul. Repita esse processo várias vezes.

Estratégia de resolução de problemas para dinâmica rotacional

1. Examine a situação para determinar se o torque e a massa estão envolvidos na rotação. Faça um esboço cuidadoso da situação.
2. Determine o sistema de interesse.
3. Desenhe um diagrama corporal gratuito. Ou seja, desenhe e rotule todas as forças externas que atuam no sistema de interesse.
4. Aplique\(net \, \tau = \alpha\),\(\alpha = \frac{net \, \tau}{I},\)
5. o equivalente rotacional da segunda lei de Newton, para resolver o problema. Deve-se tomar cuidado ao usar o momento correto de inércia e considerar o torque em torno do ponto de rotação.
6. Como sempre, verifique a solução para ver se é razoável.

Fazendo conexões: estática versus cinética

Na estática, o torque líquido é zero e não há aceleração angular. No movimento rotacional, o torque líquido é a causa da aceleração angular, exatamente como na segunda lei do movimento de rotação de Newton.

Exemplo\(\PageIndex{1}\): Calculating the Effect of Mass Distribution

Considere o pai empurrando um carrossel de parquinho na Figura. Ele exerce uma força de 250 N na borda do carrossel de 50,0 kg, que tem um raio de 1,50 m. Calcule a aceleração angular produzida (a) quando ninguém está no carrossel e (b) quando uma criança de 18,0 kg fica a 1,25 m de distância do centro. Considere o carrossel em si como um disco uniforme com atrito retardador insignificante.

Figura\(\PageIndex{4}\): Um pai empurra um carrossel de playground em sua borda e perpendicularmente ao seu raio para atingir o torque máximo.

Estratégia

A aceleração angular é dada diretamente pela expressão\(\alpha = \frac{net \, \tau}{I}\)\[\alpha = \dfrac{\tau}{I}.\] Para resolver\(\alpha\), devemos primeiro calcular o torque (que é o mesmo em ambos os casos) e o momento de inércia\(I\) (que é maior no segundo caso). Para encontrar o torque, notamos que a força aplicada é perpendicular ao raio e o atrito é insignificante, de modo que\[\tau = rF \, sin \, \theta = (1.50 \, m)(250 \, N) = 375 \, N \cdot m.\]

Solução para (a)

O momento de inércia de um disco sólido em torno desse eixo é dado na Figura para ser\[\dfrac{1}{2}MR^2,\] onde\(M = 50.0 \, kg\) e\(R = 1.50 \, m\), de modo que

\[I = (0.500)(50.0 \, kg)(1.50 \, m)^2 = 56.25 \, kg \cdot m^2\]

Agora, depois de substituirmos os valores conhecidos, descobrimos que a aceleração angular é

\[\alpha = \dfrac{\tau}{I} = \dfrac{375 \, N \cdot m}{56.25 \, kg \cdot m^2} = 6.67 \dfrac{rad}{s^2}.\]

Solução para (b)

Esperamos que a aceleração angular do sistema seja menor nessa parte, pois o momento de inércia é maior quando a criança está no carrossel. Para encontrar o momento total de inércia\(I\), primeiro encontramos o momento de inércia\(I_c\) da criança considerando que a criança é equivalente a uma massa pontual a uma distância de 1,25 m do eixo. Então,

\[I_c = MR^2 = (18.0 \, kg)(1.25 \, m)^2 = 28.13 \, kg \cdot m^2.\]

O momento total de inércia é a soma dos momentos de inércia do carrossel e da criança (aproximadamente o mesmo eixo). Para justificar essa soma para si mesmo, examine a definição de\(I\):

\[I = 28.13 \, kg \cdot m^2 + 56.25 \, kg \cdot m^2 = 84.38 \, kg \cdot m^2.\]

Substituindo valores conhecidos na equação por\(\alpha \) dá

\[\alpha = \dfrac{\tau}{I} = \dfrac{375 \, N \cdot m}{84.38 \, kg \cdot m^2} = 4.44 \dfrac{rad}{s^2}.\]

Discussão

A aceleração angular é menor quando a criança está no carrossel do que quando o carrossel está vazio, como esperado. As acelerações angulares encontradas são bastante grandes, em parte devido ao fato de o atrito ter sido considerado insignificante. Se, por exemplo, o pai continuasse pressionando perpendicularmente por 2,00 s, ele daria ao carrossel uma velocidade angular de 13,3 rad/s quando estiver vazio, mas apenas 8,89 rad/s quando a criança estiver sobre ele. Em termos de revoluções por segundo, essas velocidades angulares são 2,12 rev/s e 1,41 rev/s, respectivamente. O pai acabaria correndo a cerca de 50 km/h no primeiro caso. Jogos Olímpicos de Verão, aí vem ele! A confirmação desses números é deixada como um exercício para o leitor.

Exercício\(\PageIndex{1}\):Check Your Understanding

O torque é o análogo da força e o momento de inércia é o análogo da massa. Força e massa são quantidades físicas que dependem de apenas um fator. Por exemplo, a massa está relacionada somente ao número de átomos de vários tipos em um objeto. O torque e o momento de inércia são igualmente simples?

Solução

Não. O torque depende de três fatores: magnitude da força, direção da força e ponto de aplicação. O momento de inércia depende da massa e de sua distribuição em relação ao eixo de rotação. Portanto, embora as analogias sejam precisas, essas quantidades rotacionais dependem de mais fatores

Resumo

• Quanto mais a força é aplicada do pivô, maior é a aceleração angular; a aceleração angular é inversamente proporcional à massa.
• Se exercermos uma força\(F\) sobre uma massa pontual\(m\) que está a uma distância r de um ponto de articulação e porque a força é perpendicular a r e a aceleração\(a = F/m\) é obtida na direção de\(F\). Podemos reorganizar essa equação de forma que\[F = ma,\], em seguida, procurar maneiras de relacionar essa expressão com expressões para quantidades rotacionais. Observamos que\(a = r \alpha\), e substituímos essa expressão por\(F = ma\), produzindo\[F = mr\alpha\]
• O torque é a eficácia de giro de uma força. Nesse caso, porque\(F\) é perpendicular a\(r\), o torque é simples\(\tau = rF\). Se multiplicarmos os dois lados da equação acima por\(r\), obteremos torque no lado esquerdo. Ou seja,\[rF = mr^2\alpha\] ou\[\tau = mr^2\alpha.\]
• O momento de inércia\(I\) de um objeto é a soma\(MR^2\) de todas as massas pontuais das quais ele é composto. Ou seja,\[I = \sum mr^2.\]
• A relação geral entre torque, momento de inércia e aceleração angular é\[\tau = I \alpha\] ou\[\alpha = \dfrac{net \, \tau}{I}.\]

Glossário

torque

a eficácia de giro de uma força

inércia rotacional

resistência à mudança de rotação. Quanto mais inércia rotacional um objeto tiver, mais difícil será girá-lo

momento de inércia

massa vezes o quadrado da distância perpendicular do eixo de rotação; para uma massa pontual, é I=mR2 e, como qualquer objeto pode ser construído a partir de uma coleção de massas pontuais, essa relação é a base para todos os outros momentos de inércia