10.2: Cinemática do movimento rotacional

Last updated
Save as PDF

Page ID: 194822

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Observe a cinemática do movimento rotacional.
Derive equações cinemáticas rotacionais.
Avalie estratégias de resolução de problemas para cinemática rotacional.

Apenas usando nossa intuição, podemos começar a ver como as quantidades rotacionais se relacionam\(\theta, \omega\) e se\(\alpha\) relacionam umas com as outras. Por exemplo, se uma roda de motocicleta tem uma grande aceleração angular por um tempo bastante longo, ela acaba girando rapidamente e gira em várias rotações. Em termos mais técnicos, se a aceleração angular da roda\(\alpha\) for grande por um longo período de tempo\(t\), a velocidade angular final\(\omega\) e o ângulo de rotação\(\theta\) serão grandes. O movimento rotacional da roda é exatamente análogo ao fato de que a grande aceleração translacional da motocicleta produz uma grande velocidade final e a distância percorrida também será grande. Cinemática é a descrição do movimento. A cinemática do movimento rotacional descreve as relações entre ângulo de rotação, velocidade angular, aceleração angular e tempo. Vamos começar encontrando uma equação relacionada\(\omega, \alpha\),\(t\) e. Para determinar essa equação, lembramos uma equação cinemática familiar para movimento translacional ou linear:\[v = v_0 + at \, (constant \, a)\] Observe isso no movimento rotacional\(a = a_t\), e usaremos o símbolo\(a\) para aceleração tangencial ou linear a partir de agora. Como na cinemática linear, assumimos que\(a\) é constante, o que significa que a aceleração angular também\(\alpha\) é constante, porque\(a = r\alpha\). Agora, vamos substituir\(v = r\omega\) e\(a = r\alpha\) na equação linear acima:

\[rw = r\omega_o + r\alpha t,\]

O raio é\(r\) cancelado na equação, produzindo\[\omega = \omega_o + at \, (constant \, a),\] onde\(\omega_o\) está a velocidade angular inicial. Essa última equação é uma relação cinemática entre\(\omega, \alpha\), ou seja, descreve sua relação sem referência a forças ou massas que podem afetar a rotação.\(t\) Também é precisamente análoga em forma à sua contraparte translacional.

Fazendo conexões.

A cinemática do movimento rotacional é completamente análoga à cinemática translacional, apresentada pela primeira vez em Cinemática Unidimensional. A cinemática se preocupa com a descrição do movimento sem levar em conta a força ou a massa. Descobriremos que grandezas cinemáticas translacionais, como deslocamento, velocidade e aceleração, têm análogos diretos no movimento rotacional.

Começando com as quatro equações cinemáticas que desenvolvemos na Cinemática Unidimensional, podemos derivar as seguintes quatro equações cinemáticas rotacionais (apresentadas junto com suas contrapartes translacionais):

Tabela\(\PageIndex{1}\)
Rotacional	Translacional
\(\theta = \overline{\omega} t\)	\(x = \overline{v}t\)
\(\omega = \omega_o + \alpha t\)	\(v = v_o +at\)	\((constant \, \alpha, a)\)
\(\Theta = \omega_ot + \frac{1}{2}\alpha t^2\)	\(x = v_0t + \frac{1}{2}at^2\)	\((constant \, \alpha, a)\)
\(\omega^2 = \omega_o^2 + 2\alpha \theta\)	\(v^2 = v_0^2 + 2 ax\)	\((constant \, \alpha, a)\)

Nessas equações, o subscrito 0 indica valores iniciais (\(\theta_0, x_0\)e\(t_0\) são valores iniciais), e a velocidade angular média\(overline{\omega}\) e a velocidade média\(\overline{v}\) são definidas da seguinte forma:

\[\overline{\omega} = \dfrac{\omega_0 + \omega}{2} \, and \, \overline{v} = \dfrac{v_0 + v}{2}.\]

As equações dadas acima na Tabela\(\PageIndex{1}\) podem ser usadas para resolver qualquer problema de cinemática rotacional ou translacional no qual\(a\) e\(\alpha\) sejam constantes.

Estratégia de resolução de problemas para cinemática rotacional

Examine a situação para determinar se a cinemática rotacional (movimento rotacional) está envolvida. A rotação deve estar envolvida, mas sem a necessidade de considerar forças ou massas que afetam o movimento.
Identifique exatamente o que precisa ser determinado no problema (identifique as incógnitas). Um esboço da situação é útil.
Faça uma lista do que é dado ou pode ser inferido do problema conforme declarado (identifique os conhecidos).
Resolva a equação ou equações apropriadas para a quantidade a ser determinada (a desconhecida). Pode ser útil pensar em termos de um análogo translacional, porque agora você está familiarizado com esse movimento.
Substitua os valores conhecidos junto com suas unidades na equação apropriada e obtenha soluções numéricas completas com unidades. Certifique-se de usar unidades de radianos para ângulos.
Verifique sua resposta para ver se é razoável: Sua resposta faz sentido?

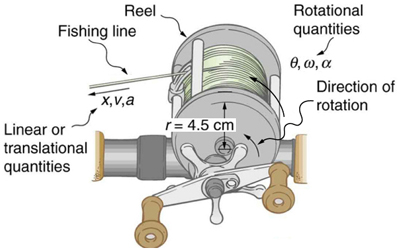
A figura mostra um carretel de pesca, com raio igual a 4,5 centímetros. A direção de rotação da bobina é no sentido anti-horário. As quantidades rotacionais são teta, ômega e alfa, e x, v, a são quantidades lineares ou translacionais. O carretel, a linha de pesca e a direção do movimento foram indicados separadamente por setas curvas apontando para essas partes. — Figura\(\PageIndex{1}\): A linha de pesca que sai de uma bobina giratória se move linearmente. Exemplo e exemplo consideram as relações entre quantidades rotacionais e lineares associadas a um carretel de pesca.

Exemplo\(\PageIndex{1}\): Calculating the Acceleration of a Fishing Reel

Um pescador de alto mar fisga um peixe grande que nada para longe do barco, puxando a linha de pesca de seu carretel de pesca. Todo o sistema está inicialmente em repouso e a linha de pesca se desenrola do carretel em um raio de 4,50 cm de seu eixo de rotação. O carretel recebe uma aceleração angular\(110 \, rad/s^2\) de 2,00 s, conforme visto na Figura 10.3.1.

Qual é a velocidade angular final da bobina?
A que velocidade a linha de pesca sai do carretel após decorridos 2,00 s?
Quantas revoluções a bobina faz?
Quantos metros de linha de pesca saem do carretel neste momento?

Estratégia

Em cada parte desse exemplo, a estratégia é a mesma de resolver problemas em cinemática linear. Em particular, valores conhecidos são identificados e, em seguida, busca-se uma relação que possa ser usada para resolver o desconhecido.

Solução para (a)

Aqui\(\alpha\) e\(t\) são dados e\(\omega\) precisam ser determinados. A equação mais simples de usar é\(\omega = \omega_0 + \alpha t\) porque o desconhecido já está de um lado e todos os outros termos são conhecidos. Essa equação afirma que

\[\omega = \omega_0 + \alpha t.\]

Também recebemos isso\(\omega_0 = 0\) (começa do descanso), de modo que

\[\omega = 0 + (110 \, rad/s^2)(2.00s) = 220 \, rad/s.\]

Solução para (b)

Agora que\(\omega\) se sabe, a velocidade\(v\) pode ser mais facilmente encontrada usando a relação em\[v = r\omega,\] que o raio\(r\) da bobina é dado em 4,50 cm; portanto,\[ v = (0.0450 \, m)(220 \, rad/s) = 9.90 \, m/s.\] observe novamente que os radianos devem sempre ser usados em qualquer cálculo relacionado a quantidades lineares e angulares. Além disso, como os radianos são adimensionais, nós temos\(m \times rad = m\).

Solução para (c)

Aqui, somos convidados a encontrar o número de revoluções. Porque\(1\space rev = 2\pi \, rad\) podemos encontrar o número de revoluções encontrando\(\theta\) em radianos. Recebemos\(\alpha\) e\(t\), e sabemos que\(\omega_o\) é zero, então isso\(\theta\) pode ser obtido usando\(\theta = \omega_0t + \frac{1}{2}\alpha t^2\).

\[\theta = \omega_0t + \dfrac{1}{2} \alpha t^2\]

\[= 0 + (0.500)(110 \, rad/s^2)(2.00s)^2 = 220 rad.\]

A conversão de radianos em revoluções dá\[\theta = (220 \, rad)\dfrac{1 \, rev}{2\pi \, rad} = 35.0 \, rev.\]

Solução para (d)

O número de metros de linha de pesca é\(x\) o que pode ser obtido por meio de sua relação com\(\theta\).

\[x = r\theta = (0.0450 \, m)(220 \, rad) = 9.90 \, m.\]

Discussão

Este exemplo ilustra que as relações entre quantidades rotacionais são altamente análogas às relações entre quantidades lineares. Também vemos neste exemplo como quantidades lineares e rotacionais estão conectadas. As respostas às perguntas são realistas. Depois de desenrolar por dois segundos, verifica-se que a bobina gira a 220 rad/s, o que é 2100 rpm. (Não é de admirar que os rolos às vezes emitam sons agudos.) A quantidade de linha de pesca usada é de 9,90 m, quase a certa para quando o peixe grande morde.

Exemplo\(\PageIndex{2}\): Calculating the Duration When the Fishing Reel Slows Down and Stops

Agora, vamos considerar o que acontece se o pescador acionar um freio na bobina giratória, alcançando uma aceleração angular de -\(300 \, rad/s^2\). Quanto tempo a bobina demora para parar?

Estratégia

Somos convidados a encontrar tempo para que a bobina pare. As condições iniciais e finais são diferentes das do problema anterior, que envolvia o mesmo carretel de pesca. Agora vemos que a velocidade angular inicial é\(\omega_0 = 220 \, rad/s\) e a velocidade angular final\(\omega\) é zero. A aceleração angular é dada para\(\alpha = - 300 \, rad/s^2.\) examinar as equações disponíveis, vemos todas as quantidades, exceto t, são conhecidas em\(\omega = \omega_0 + \alpha t\), facilitando o uso dessa equação.

Solução

Os estados da equação\[\omega = \omega_0 + \alpha t.\]

Resolvemos a equação algebricamente por t e, em seguida, substituímos os valores conhecidos como de costume, produzindo

\[t = \dfrac{\omega - \omega_0}{\alpha} = \dfrac{0 - 220 \, rad/s}{-300 \, rad/s^2} = 0.733 \, s.\]

Discussão

Observe que deve-se ter cuidado com os sinais que indicam as direções de várias quantidades. Além disso, observe que o tempo para parar a bobina é bastante pequeno porque a aceleração é bastante grande. As linhas de pesca às vezes quebram por causa das acelerações envolvidas, e os pescadores costumam deixar o peixe nadar por um tempo antes de acionar os freios no carretel. Um peixe cansado será mais lento, exigindo uma aceleração menor.

Exemplo\(\PageIndex{3}\): Calculating the Slow Acceleration of Trains and Their Wheels

Grandes trens de carga aceleram muito lentamente. Suponha que um desses trens acelere do repouso, dando às rodas de 0,350 m de raio uma aceleração angular de\(0.250 \, rad/s^2\). Depois que as rodas tiverem feito 200 rotações (suponha que não haja derrapagem): (a) Até onde o trem desceu os trilhos? (b) Qual é a velocidade angular final das rodas e a velocidade linear do trem?

Estratégia

Em parte (a), somos convidados a encontrar\(x\), e em (b) somos convidados a encontrar\(\omega\)\(v\) e. Recebemos o número de revoluções\(\theta\), o raio das rodas\(r\) e a aceleração angular\(\alpha\).

Solução para (a)

A distância\(x\) é facilmente encontrada a partir da relação entre a distância e o ângulo de rotação:

\[\theta = \dfrac{x}{r}.\]

Resolvendo essa equação para\(x\) rendimentos\[x = r\theta.\]

Antes de usar essa equação, devemos converter o número de revoluções em radianos, porque estamos lidando com uma relação entre quantidades lineares e rotacionais:

\[\theta = (200 \, rev)\dfrac{2\pi \, rad}{1 \, rev} = 1257 \, rad.\]

Agora podemos substituir os valores conhecidos em\(x = r\theta\) para encontrar a distância que o trem percorreu pela pista:

\[x = r\theta = (0.350 \, m)(1257 \, rad) = 440 \, m.\]

Solução para (b)

Não podemos usar nenhuma equação que incorpore\(t\) para encontrar\(\omega\), porque a equação teria pelo menos dois valores desconhecidos. A equação\(\omega^2 = \omega_0^2 + 2\alpha \theta\) funcionará, porque sabemos os valores de todas as variáveis, exceto\(\omega\).

\[\omega^2 = \omega_0^2 + 2 \alpha \theta\]

Tomando a raiz quadrada dessa equação e inserindo os valores conhecidos, obtemos

\[\omega = [0 + 2(0.250 \, rad/s^2)(1257 \, rad)]^{1/2}\]

\[= 25.1 \, rad/s.\]

Podemos encontrar a velocidade linear do trem,\(v\), por meio de sua relação com\(\omega\):

\[v = r\omega = (0.350 \, m)(25.1 \, rad/s) = 8.77 \, m/s.\]

Discussão

A distância percorrida é bastante grande e a velocidade final é bastante lenta (pouco menos de 32 km/h).

Há movimento translacional até mesmo para algo girando no lugar, como ilustra o exemplo a seguir. A Figura 10.3.2 mostra uma mosca na borda de uma placa giratória de forno de microondas. O exemplo abaixo calcula a distância total percorrida.

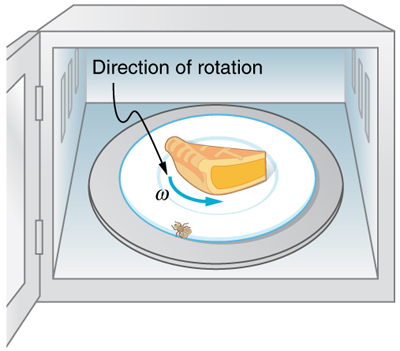
A figura mostra uma mosca que pousou na placa giratória do micro-ondas. A direção de rotação da placa, ômega, é no sentido anti-horário e é mostrada com uma seta. — Figura\(\PageIndex{2}\). A imagem mostra uma placa de microondas. A mosca faz revoluções enquanto a comida é aquecida (junto com a mosca).

Exemplo\(\PageIndex{4}\): Calculating the Distance Traveled by a Fly on the Edge of a Microwave Oven Plate

Uma pessoa decide usar um forno de microondas para reaquecer o almoço. No processo, uma mosca voa acidentalmente para o microondas e pousa na borda externa da placa giratória e permanece lá. Se a placa tiver um raio de 0,15 m e girar a 6,0 rpm, calcule a distância total percorrida pela mosca durante um período de cozimento de 2,0 minutos. (Ignore os tempos de inicialização e desaceleração.)

Estratégia

Primeiro, encontre o número total de revoluções e\(\theta\), em seguida, a distância linear\(x\) percorrida. \(\theta = \overline{\omega}\)pode ser usado para encontrar\(\theta\) porque\(\overline{\omega}\) é fornecido como sendo de 6,0 rpm.

Solução

Inserindo valores conhecidos em\(\theta = \overline{\omega}\) dá\[\theta = \overline{\omega} = (6.0 \, rpm)(2.0 \, min) = 12 \, rev.\]

Como sempre, é necessário converter revoluções em radianos antes de calcular uma quantidade linear, como\(x\) a partir de uma quantidade angular como\(\theta\):

\[\theta = (12 \, rev)\left(\dfrac{2\pi \, rad}{1 \, rev}\right) = 75.4 \, rad.\]

Agora, usando a relação entre\(x\) e\(\theta\), podemos determinar a distância percorrida:

\[x = r\theta = (0.15 \, m)(75.4 \, rad) = 11 \, m.\]

Discussão

Uma boa viagem (se sobreviver)! Observe que essa distância é a distância total percorrida pela mosca. O deslocamento é, na verdade, zero para revoluções completas porque elas trazem a mosca de volta à sua posição original. A distinção entre a distância total percorrida e o deslocamento foi observada pela primeira vez em Cinemática Unidimensional.

Exercício\(\PageIndex{1}\)

A cinemática rotacional tem muitas relações úteis, geralmente expressas em forma de equação. Essas relações são leis da física ou são simplesmente descritivas? (Dica: a mesma pergunta se aplica à cinemática linear.)

Responda: A cinemática rotacional (assim como a cinemática linear) é descritiva e não representa as leis da natureza. Com a cinemática, podemos descrever muitas coisas com grande precisão, mas a cinemática não considera as causas. Por exemplo, uma grande aceleração angular descreve uma mudança muito rápida na velocidade angular sem qualquer consideração de sua causa.

Resumo

Cinemática é a descrição do movimento.
A cinemática do movimento rotacional descreve as relações entre ângulo de rotação, velocidade angular, aceleração angular e tempo.
Começando com as quatro equações cinemáticas que desenvolvemos na Cinemática Unidimensional, podemos derivar as quatro equações cinemáticas rotacionais (apresentadas junto com suas contrapartes translacionais) vistas na Tabela.
Nessas equações, o subscrito 0 indica valores iniciais (\(({x_0}\)e\(t_o\) são valores iniciais), e a velocidade angular média\(\overline{\omega}\) e a velocidade média\(\overline{v}\) são definidas da seguinte forma:\[ \overline{\omega} = \dfrac{\omega_0 + \omega}{2} \, and \, \dfrac{v_0 + v}{2}.\]

Glossário

cinemática do movimento rotacional: descreve as relações entre ângulo de rotação, velocidade angular, aceleração angular e tempo