10.1: Aceleração angular

Last updated
Save as PDF

Page ID: 194858

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Descreva o movimento circular uniforme.
Explique o movimento circular não uniforme.
Calcule a aceleração angular de um objeto.
Observe a ligação entre a aceleração linear e angular.

Movimento circular uniforme e gravitação discutiram apenas o movimento circular uniforme, que é o movimento em um círculo em velocidade constante e, portanto, velocidade angular constante. Lembre-se de que a velocidade angular\(\omega\) foi definida como a taxa de tempo de mudança de ângulo\(\theta\).

\[ \omega = \dfrac{\Delta \theta}{\Delta t},\]

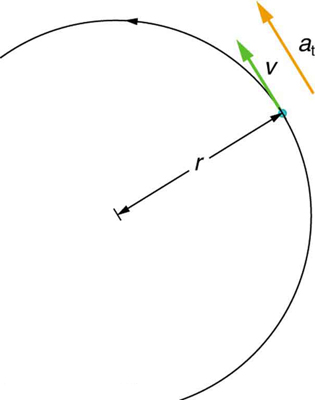
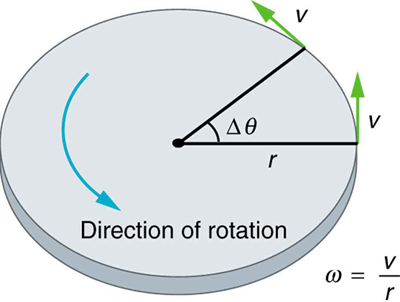
onde\(\theta\) está o ângulo de rotação, conforme visto na Figura\(\PageIndex{1}\). A relação entre velocidade angular\(\omega\) e velocidade linear também\(v\) foi definida em Ângulo de Rotação e Velocidade Angular como

\[v = r \omega\]

\[\omega = \dfrac{v}{r}\]

onde\(r\) está o raio de curvatura, também visto na Figura\(\PageIndex{1}\). De acordo com a convenção de sinais, a direção anti-horária é considerada como positiva e a direção horária como negativa

A figura dada mostra o movimento circular no sentido anti-horário com uma linha horizontal, representando o raio r, desenhado do centro do círculo para o lado direito em sua circunferência e outra linha é desenhada de forma a formar um ângulo agudo delta teta com a linha horizontal. Os vetores de velocidade tangencial são indicados no final das duas linhas. No canto inferior direito da figura, a fórmula da velocidade angular é dada como v sobre r. — Figura\(\PageIndex{1}\): Esta figura mostra um movimento circular uniforme e algumas de suas quantidades definidas.

A velocidade angular não é constante quando uma patinadora puxa seus braços, quando uma criança inicia um carrossel do repouso ou quando o disco rígido do computador fica lento até parar quando desligado. Em todos esses casos, há uma aceleração angular, na qual\(\omega\) muda. Quanto mais rápida a mudança ocorrer, maior será a aceleração angular. \(\alpha\)A aceleração angular é definida como a taxa de variação da velocidade angular. Em forma de equação, a aceleração angular é expressa da seguinte forma:

\[\alpha = \dfrac{\Delta \omega}{\Delta t},\]onde\(Δω\) está a mudança na velocidade angular e\(Δt\) é a mudança no tempo. As unidades de aceleração angular são (rad/s) /s ou rad/\(s^2\). Se\(ω\) aumentar, então\(α\) é positivo. Se\(ω\) diminuir, então\(α\) é negativo.

Exemplo\(\PageIndex{1}\): Calculating the Angular Acceleration and Deceleration of a Bike Wheel

Suponha que uma adolescente coloque a bicicleta de costas e faça a roda traseira girar do repouso até uma velocidade angular final de 250 rpm em 5,00 s. (a) Calcule a aceleração angular em\(rad/s^2\). (b) Se ela agora pisar no freio, causando uma aceleração angular de —87,3\(rad/s^2\), quanto tempo o volante leva para parar?

Estratégia para (a)

A aceleração angular pode ser encontrada diretamente de sua definição\(α=\frac{Δω}{Δt}\) porque a velocidade angular final e o tempo são fornecidos. Vemos que\(Δω\) é de 250 rpm e\(Δt\) é de 5,00 s.

Solução para (a)

Inserindo informações conhecidas na definição de aceleração angular, obtemos

\(α=\frac{Δω}{Δt}=\frac{250 rpm}{5.00 s}\).

Como\(Δω\) está em rotações por minuto (rpm) e queremos as unidades padrão de\(rad/s^2\) para aceleração angular, precisamos converter\(Δω\) de rpm para rad/s:

\(Δω=250\frac{rev}{min}⋅\frac{2π rad}{rev}⋅\frac{1 min}{60 sec}=26.2rads\).

Inserindo essa quantidade na expressão para\(α\), obtemos

\(α=\frac{Δω}{Δt}=\frac{26.2 rad/s}{5.00 s}=5.24 rad/s^2\).

Estratégia para (b)

Nesta parte, conhecemos a aceleração angular e a velocidade angular inicial. Podemos encontrar o tempo de parada usando a definição de aceleração angular e resolvendo Δt, produzindo

\(Δt=\frac{Δω}{α}\).

Solução para (b)

Aqui, a velocidade angular diminui de 26,2 rad/s (250 rpm) para zero, ou\(Δω\) seja, —26,2 rad/s, e α é dado como —87,3\(rad/s^2\). Assim,

\(Δt=\frac{–26.2 rad/s}{–87.3rad/s^2}=0.300 s.\)

Discussão

Observe que a aceleração angular quando a garota gira a roda é pequena e positiva; são necessários 5 s para produzir uma velocidade angular apreciável. Quando ela pisa no freio, a aceleração angular é grande e negativa. A velocidade angular rapidamente chega a zero. Em ambos os casos, as relações são análogas ao que acontece com o movimento linear. Por exemplo, há uma grande desaceleração quando você colide com uma parede de tijolos — a mudança de velocidade é grande em um curto intervalo de tempo.

Se a bicicleta do exemplo anterior estivesse sobre suas rodas em vez de invertida, ela primeiro teria acelerado ao longo do solo e depois parado. Essa conexão entre movimento circular e movimento linear precisa ser explorada. Por exemplo, seria útil saber como as acelerações lineares e angulares estão relacionadas. Em movimento circular, a aceleração linear é tangente à circunferência no ponto de interesse, como visto na Figura\(\PageIndex{2}\). Assim, a aceleração linear é chamada de aceleração tangencial\(a_t\).

Figura\(\PageIndex{2}\): Em movimento circular, a aceleração\(a\) linear ocorre à medida que a magnitude da velocidade muda:\(a\) é tangente ao movimento. No contexto do movimento circular, a aceleração linear também é chamada de aceleração tangencial\(a_t\).

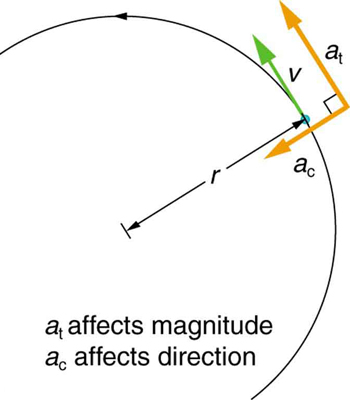
A aceleração linear ou tangencial se refere a mudanças na magnitude da velocidade, mas não em sua direção. Sabemos pelo Movimento Circular Uniforme e Gravitação que, no movimento circular, a aceleração centrípeta, ac, se refere a mudanças na direção da velocidade, mas não em sua magnitude. Um objeto em movimento circular experimenta aceleração centrípeta, como visto na Figura\(\PageIndex{3}\). Assim,\(a_t\) e\(a_c\) são perpendiculares e independentes um do outro. A aceleração tangencial\(a_t\) está diretamente relacionada à aceleração angular\(α\) e está ligada a um aumento ou diminuição na velocidade, mas não em sua direção.

Na figura, um semicírculo é desenhado, com seu raio r, mostrado aqui como um segmento de linha. O movimento anti-horário do círculo é mostrado com uma seta no caminho do círculo. O vetor de velocidade tangencial, v, do ponto, que está no ponto de encontro do raio com o círculo, é mostrado como uma seta verde e a aceleração linear, um sub t é mostrado como uma seta amarela na mesma direção ao longo de v. A aceleração centrípeta, a sub c, também é mostrada como uma seta amarela desenhada perpendicularmente para um subt, em direção à direção do centro do círculo. Um rótulo nas figuras afirma que um sub t afeta a magnitude e um sub c afeta a direção. — Figura\(\PageIndex{3}\): A aceleração centrípeta\(a_c\) ocorre à medida que a direção da velocidade muda; ela é perpendicular ao movimento circular. A aceleração centrípeta e tangencial é, portanto, perpendicular uma à outra.

Agora podemos encontrar a relação exata entre aceleração linear\(a_t\) e aceleração angular\(α\). Como a aceleração linear é proporcional a uma mudança na magnitude da velocidade, ela é definida (como era na Cinemática Unidimensional) como

\(a_t=\frac{Δv}{Δt}\).

Para movimentos circulares, observe que\(v=rω\), para que

\(a_t=\frac{Δ(rω)}{Δt}\).

O raio r é constante para movimentos circulares, e assim\(Δ(rω)=r(Δω)\). Assim,

\(a_t=r\frac{Δω}{Δt}\).

Por definição,\(α=\frac{Δω}{Δt}\). Assim,

\(a_t=rα\),

\(α=\frac{a_t}{r}\).

Essas equações significam que a aceleração linear e a aceleração angular são diretamente proporcionais. Quanto maior for a aceleração angular, maior será a aceleração linear (tangencial) e vice-versa. Por exemplo, quanto maior a aceleração angular das rodas motrizes de um carro, maior a aceleração do carro. O raio também é importante. Por exemplo, quanto menor for uma roda, menor será sua aceleração linear para uma determinada aceleração angular\(α\).

Exercício\(\PageIndex{1}\): Calculating the Angular Acceleration of a Motorcycle Wheel

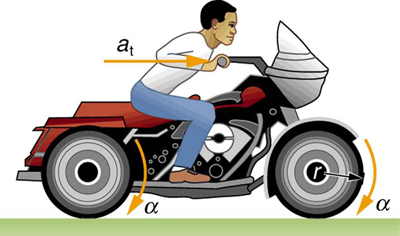
Uma motocicleta potente pode acelerar de 0 a 30,0 m/s (cerca de 108 km/h) em 4,20 s. Qual é a aceleração angular de suas rodas de 0,320 m de raio? (Veja a Figura.)

A figura mostra a visão lateral direita de um homem dirigindo uma motocicleta, portanto, representando a aceleração linear a da motocicleta apontando para a frente da bicicleta como uma seta horizontal e a aceleração angular alfa de suas rodas, mostrada aqui como setas curvas ao longo da frente de ambas as rodas apontando para baixo. — Figura\(\PageIndex{4}\): A aceleração linear de uma motocicleta é acompanhada por uma aceleração angular de suas rodas.

Estratégia

Recebemos informações sobre as velocidades lineares da motocicleta. Assim, podemos encontrar sua aceleração linear\(a_t\). Então, a expressão\(α=\frac{a_t}{r}\) pode ser usada para encontrar a aceleração angular.

Solução

A aceleração linear é

\(a_t=\frac{Δv}{Δt}=\frac{30.0 m/s}{4.20 s}=7.14m/s^2\).

Também sabemos o raio das rodas. Inserindo os valores para\(a_t\) e\(r\) para\(α=\frac{a_t}{r}\), obtemos

\(α=\frac{a_t}{r}=\frac{7.14m/s^2}{0.320 m}=22.3rad/s^2\).

Discussão

As unidades de radianos são adimensionais e aparecem em qualquer relação entre quantidades angulares e lineares.

Até agora, definimos três quantidades rotacionais -\(θ, ω,\)\(α\) e. Essas quantidades são análogas às quantidades translacionais\(x, v,\)\(a\) e. A tabela\(\PageIndex{2}\) exibe as quantidades rotacionais, as quantidades translacionais análogas e as relações entre elas.

Tabela\(\PageIndex{2}\): Quantidades rotacionais e translacionais
Rotacional	Translacional	Relacionamento
\(θ\)	\(x\)	\(θ=\frac{x}{r}\)
\(ω\)	\(v\)	\(ω=\frac{v}{r}\)
\(α\)	\(a\)	\(α=\frac{a_t}{r}\)

FAZENDO CONEXÕES: EXPERIMENTO PARA LEVAR PARA CASA

Sente-se com os pés no chão em uma cadeira que gira. Levante uma das pernas de forma que fique solta (esticada). Usando a outra perna, comece a girar empurrando o chão. Pare de usar a perna para empurrar o chão, mas deixe a cadeira girar. Da origem onde você começou, esboce o ângulo, a velocidade angular e a aceleração angular de sua perna em função do tempo na forma de três gráficos separados. Estime as magnitudes dessas quantidades.

Exercício\(\PageIndex{2}\)

A aceleração angular é um vetor, com magnitude e direção. Como denotamos sua magnitude e direção? Ilustre com um exemplo.

Responda: A magnitude da aceleração angular é\(α\) e suas unidades mais comuns são\(rad/s^2\). A direção da aceleração angular ao longo de um eixo fixo é indicada por um sinal de + ou a —, assim como a direção da aceleração linear em uma dimensão é indicada por um sinal + ou um —. Por exemplo, considere uma ginasta fazendo uma virada para frente. Seu impulso angular seria paralelo ao tapete e à esquerda. A magnitude de sua aceleração angular seria proporcional à sua velocidade angular (taxa de rotação) e seu momento de inércia em torno de seu eixo de rotação.

EXPLORAÇÕES DE PHET: A REVOLUÇÃO DA JOANINHA

Junte-se à Ladybug Revolution em uma exploração do movimento rotacional. Gire o carrossel para alterar seu ângulo ou escolha uma velocidade angular constante ou aceleração angular. Explore como o movimento circular se relaciona com a posição x, y, velocidade e aceleração do bug usando vetores ou gráficos.

Resumo

O movimento circular uniforme é o movimento com uma velocidade angular constante\(ω=\frac{Δθ}{Δt}\).
Em movimentos circulares não uniformes, a velocidade muda com o tempo e a taxa de mudança da velocidade angular (ou seja, aceleração angular) é\(α=\frac{Δω}{Δt}\).
A aceleração linear ou tangencial se refere a mudanças na magnitude da velocidade, mas não em sua direção, dada como\(a_t=\frac{Δv}{Δt}\).
Para movimentos circulares, observe que\(v=rω\), para que
\(a_t=\frac{Δ(rω)}{Δt}\).
O raio r é constante para movimentos circulares, e assim\(Δ(rω)=rΔω\). Assim,
\(a_t=r\frac{Δω}{Δt}\).
Por definição,\(Δω/Δt=α\). Assim,
\(a_t=rα\)

ou

\(α=\frac{a_t}{r}\).

Glossário

aceleração angular: a taxa de mudança da velocidade angular com o tempo

mudança na velocidade angular: a diferença entre os valores finais e iniciais da velocidade angular

aceleração tangencial: a aceleração em uma direção tangente à circunferência no ponto de interesse em movimento circular