10.4: Energia Cinética Rotacional - Trabalho e Energia Revisitados

Objetivos de

Ao final desta seção, você poderá:

• Derive a equação para o trabalho rotacional.
• Calcule a energia cinética rotacional.
• Demonstre a Lei de Conservação de Energia.

Neste módulo, aprenderemos sobre trabalho e energia associados ao movimento rotacional. A figura\(\PageIndex{1}\) mostra um trabalhador usando um rebolo elétrico impulsionado por um motor. Faíscas estão voando e ruídos e vibrações são criados à medida que camadas de aço são retiradas do poste. A pedra continua girando mesmo depois que o motor é desligado, mas acaba sendo interrompida por atrito. Claramente, o motor teve que funcionar para fazer a pedra girar. Esse trabalho envolveu calor, luz, som, vibração e considerável energia cinética rotacional.

Figura\(\PageIndex{1}\): O motor funciona girando a pedra de amolar, fornecendo energia cinética rotacional. Essa energia é então convertida em calor, luz, som e vibração. (crédito: foto da Marinha dos EUA do marinheiro especialista em comunicação de massa Zachary David Bell)

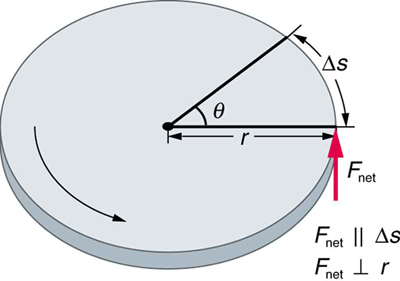
O trabalho deve ser feito para girar objetos, como rebolos ou carrossel. O trabalho foi definido em Movimento Circular Uniforme e Gravitação para movimento translacional, e podemos aproveitar esse conhecimento ao considerar o trabalho realizado em movimento rotacional. A situação rotacional mais simples é aquela em que a força líquida é exercida perpendicularmente ao raio de um disco (conforme mostrado na Figura\(\PageIndex{2}\)) e permanece perpendicular à medida que o disco começa a girar. A força é paralela ao deslocamento e, portanto, o trabalho em rede realizado é o produto da força vezes o comprimento do arco percorrido:

\[net \, W = (net \, F)\Delta s.\]

Para inserir torque e outras grandezas rotacionais na equação, multiplicamos e dividimos o lado direito da equação por\(r\) e reunimos os termos:

\[net \, W = (r \, net \, F)\dfrac{\Delta s}{r}.\]

Nós reconhecemos isso\(r\)\(net \, F = net \, \tau\) e\(\Delta s/r = \theta\), para que

\[net \, W = (net \, \tau)\theta. \label{netw}\]

Essa equação é a expressão do trabalho rotacional. É muito semelhante à definição familiar de trabalho translacional como força multiplicada pela distância. Aqui, o torque é análogo à força e o ângulo é análogo à distância. A equação\ ref {netw} é válida em geral, embora tenha sido derivada para um caso especial. Para obter uma expressão para a energia cinética rotacional, devemos novamente realizar algumas manipulações algébricas. O primeiro passo é observar que

\[net \, W = I \alpha \theta\]

Figura\(\PageIndex{2}\): A força líquida neste disco é mantida perpendicular ao seu raio, pois a força faz com que o disco gire. O trabalho em rede realizado é, portanto,\((net \, F)\Delta s.\) o trabalho em rede entra em energia cinética rotacional.

O trabalho e a energia no movimento rotacional são completamente análogos ao trabalho e à energia no movimento translacional, apresentados pela primeira vez em Movimento Circular Uniforme e Gravitação.

Agora, resolvemos uma das equações da cinemática rotacional para\(\alpha \theta\). Começamos com a equação

\[\omega^2 = \omega_0^2 + 2\alpha \theta.\]

Em seguida, resolvemos\(\alpha \theta\):

\[\alpha \theta = \dfrac{\omega^2 - \omega_0^2}{2}.\]

Substituindo isso na equação por rendimentos de termos líquidos\(W\) e de coleta

\[net \, W = \dfrac{1}{2}I\omega^2 - \dfrac{1}{2}I\omega_0^2.\]

Essa equação é o teorema da energia de trabalho apenas para movimento rotacional. Como você deve se lembrar, a rede altera a energia cinética de um sistema. Por meio de uma analogia com o movimento translacional, definimos o termo\(\left(\frac{1}{2}\right)\omega^2\) como energia cinética rotacional\(KE_{rot}\) para um objeto com um momento de inércia\(I\) e uma velocidade angular\(\omega\):

\[KE_{rot} = \dfrac{1}{2}I \omega^2.\]

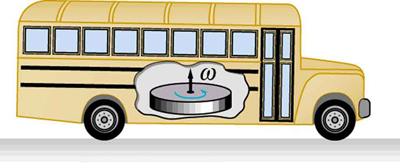
A expressão para energia cinética rotacional é exatamente análoga à energia cinética translacional,\(I\) sendo análoga\(\omega\) a\(m\) e\(v\) a. A energia cinética rotacional tem efeitos importantes. Os volantes, por exemplo, podem ser usados para armazenar grandes quantidades de energia cinética rotacional em um veículo, conforme visto na Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Veículos experimentais, como este ônibus, foram construídos nos quais a energia cinética rotacional é armazenada em um grande volante. Quando o ônibus desce uma colina, sua transmissão converte sua energia potencial gravitacional em\(KE_{rot}\). Também pode converter energia cinética translacional, quando o ônibus para, em\(KE_{rot}\). A energia do volante pode então ser usada para acelerar, subir outra colina ou evitar que o ônibus diminua a velocidade devido ao atrito.

Exemplo\(\PageIndex{1}\): Calculating the Work and Energy for Spinning a Grindstone

Considere uma pessoa que gira uma grande pedra de amolar colocando a mão na borda e exercendo uma força durante parte de uma revolução, conforme mostrado na Figura. Neste exemplo, verificamos que o trabalho realizado pelo torque que ela exerce é igual à mudança na energia rotacional.

1. Quanto trabalho é feito se ela exercer uma força de 200 N através de uma rotação de\(1.00 \, rad(57.3^o)\)? A força é mantida perpendicular ao raio de 0,320 m do rebolo no ponto de aplicação, e os efeitos do atrito são insignificantes.
2. Qual é a velocidade angular final se o rebolo tiver uma massa de 85,0 kg?
3. Qual é a energia cinética rotacional final? (Deve ser igual ao trabalho.)

Estratégia

Para encontrar o trabalho, podemos usar a Equação\ ref {netw}. Temos informações suficientes para calcular o torque e recebemos o ângulo de rotação. Na segunda parte, podemos encontrar a velocidade angular final usando uma das relações cinemáticas. Na última parte, podemos calcular a energia cinética rotacional a partir de sua expressão em\(KE_{rot} = \frac{1}{2}I\omega^2\).

Solução para (a)

A rede é expressa na equação

\[net \, W = (net \, \tau)\theta,\]

onde net\(\tau\) é a força aplicada multiplicada pelo raio\((rF)\) porque não há atrito retardador e a força é perpendicular\(r\) a. O ângulo\(\theta\) é dado. Substituir os valores dados na equação acima resulta

\[\begin{align*} net \, W &= rF\theta \\[5pt] &= (0.320 \, m)(200 \, N)(1.00 \, rad) \\[5pt] &= 64.0 \, N \cdot m. \end{align*}\]

Observando que\(1 \, N \cdot m = 1 \, J.\),

\[net \, W = 64.0 \, J.\]

Figura\(\PageIndex{4}\). Uma grande pedra de amolar é girada por uma pessoa que agarra sua borda externa.

Solução para (b)

Para encontrar a\(\omega\) partir das informações fornecidas, é necessário mais de uma etapa. Começamos com a relação cinemática na equação

\[\omega^2 = \omega_0^2 + 2 \alpha \theta.\]

Note isso\(\omega_0 = 0\) porque partimos do descanso. Tomando a raiz quadrada da equação resultante,\[\omega = (2\alpha \theta)^{1/2}.\] agora precisamos encontrar\(\alpha.\) Uma possibilidade é\[\alpha = \dfrac{net \, \tau}{I},\]

onde está o torque

\[net \, \tau = rF = (0.320 \, m)(200 \, N) = 64.0 \, N \cdot m.\]

A fórmula para o momento de inércia de um disco é encontrada em [link]:

\[I = \dfrac{1}{2}MR^2 = 0.5(85.0 \, kg)(0.320 \, m)^2 = 4.352 \, kg \cdot m^2.\]

Substituindo os valores de torque e momento de inércia na expressão por\(\alpha\), obtemos

\[\alpha = \dfrac{64.0 \, N\cdot m}{4.352 \, kg \cdot m^2} = 14.7 \dfrac{rad}{s^2}.\]

Agora, substitua esse valor e o valor fornecido\(\theta \) na expressão acima por\(\omega\):

\[\omega = (2\alpha \theta)^{1/2} = [2(14.7 \dfrac{rad}{s^2})(1.00 \, rad)]^{1/2} = 5.42 \dfrac{rad}{s}.\]

Solução para (c)

A energia cinética rotacional final é\[KE_{rot} = \dfrac{1}{2}I\omega^2.\]

Ambos\(I\)\(\omega\) foram encontrados acima. Assim,

\ [KE_ {rot} = (0,5) (4,352\, kg\ cdot m^2) (5,42\, rad/s) ^2 = 64,0\, J.

Discussão

A energia cinética rotacional final é igual ao trabalho realizado pelo torque, o que confirma que o trabalho realizado foi transformado em energia cinética rotacional. Poderíamos, de fato, ter usado uma expressão para energia em vez de uma relação cinemática para resolver a parte (b). Faremos isso em exemplos posteriores.

Os pilotos de helicóptero estão bastante familiarizados com a energia cinética rotacional. Eles sabem, por exemplo, que um ponto sem retorno será alcançado se permitirem que suas lâminas diminuam abaixo de uma velocidade angular crítica durante o voo. As lâminas perdem sustentação e é impossível fazer com que as lâminas girem imediatamente rápido o suficiente para recuperá-las. A energia cinética rotacional deve ser fornecida às pás para que elas girem mais rápido, e energia suficiente não pode ser fornecida a tempo para evitar um acidente. Devido às limitações de peso, os motores dos helicópteros são muito pequenos para fornecer a energia necessária para a elevação e para reabastecer a energia cinética rotacional das pás depois que elas diminuem a velocidade. A energia cinética rotacional é colocada neles antes da decolagem e não se deve permitir que caia abaixo desse nível crucial. Uma maneira possível de evitar um acidente é usar a energia potencial gravitacional do helicóptero para reabastecer a energia cinética rotacional das pás, perdendo altitude e alinhando as pás para que o helicóptero seja girado para cima na descida. Obviamente, se a altitude do helicóptero for muito baixa, não haverá tempo suficiente para que a lâmina recupere a sustentação antes de chegar ao solo.

Estratégia de resolução de problemas para energia rotacional

1. Determine se a energia ou o trabalho estão envolvidos na rotação.
2. Determine o sistema de interesse. Um esboço geralmente ajuda.
3. Analise a situação para determinar os tipos de trabalho e energia envolvidos.
4. Para sistemas fechados, a energia mecânica é conservada. Isso é,\(KE_i + PE_f = KE_f + PE_f\). Observe que\(KE_i \) e cada uma\(KE_f\) pode incluir contribuições translacionais e rotacionais. Para sistemas abertos, a energia mecânica pode não ser conservada e outras formas de energia (referidas anteriormente como\(OE\)),
5. como transferência de calor, pode entrar ou sair do sistema. Determine o que são e calcule-os conforme necessário.
6. Elimine termos sempre que possível para simplificar a álgebra.
7. Verifique a resposta para ver se é razoável.

Exemplo\(\PageIndex{2}\): Calculating Helicopter Energies

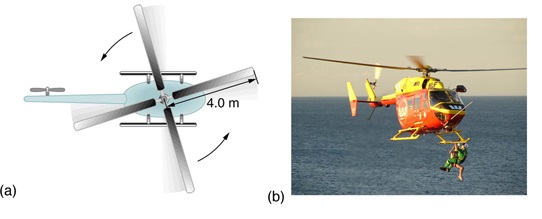
Um pequeno helicóptero de resgate típico, semelhante ao da Figura\(\PageIndex{5}\), tem quatro pás, cada uma com 4,00 m de comprimento e uma massa de 50,0 kg. As lâminas podem ser aproximadas como hastes finas que giram em torno de uma extremidade de um eixo perpendicular ao seu comprimento. O helicóptero tem uma massa total carregada de 1000 kg.

1. Calcule a energia cinética rotacional nas pás quando elas giram a 300 rpm.
2. Calcule a energia cinética translacional do helicóptero quando ele voa a 20,0 m/s e compare-a com a energia rotacional nas pás
3. Até que altura o helicóptero poderia ser elevado se toda a energia cinética rotacional pudesse ser usada para levantá-lo?

Figura\(\PageIndex{5}\): A primeira imagem mostra como os helicópteros armazenam grandes quantidades de energia cinética rotacional em suas pás. Essa energia deve ser colocada nas pás antes da decolagem e mantida até o final do voo. Os motores não têm potência suficiente para simultaneamente fornecer sustentação e colocar energia rotacional significativa nas pás. A segunda imagem mostra um helicóptero do Auckland Westpac Rescue Helicopter Service. Mais de 50.000 vidas foram salvas desde o início de suas operações em 1973. Aqui, uma operação de resgate na água é mostrada. (crédito: 111 Emergency, Flickr)

Estratégia

As energias cinéticas rotacionais e translacionais podem ser calculadas a partir de suas definições. A última parte do problema está relacionada à ideia de que a energia pode mudar de forma, neste caso, da energia cinética rotacional para a energia potencial gravitacional.

Solução para (a)

A energia cinética rotacional é

\[KE_{rot} = \dfrac{1}{2}I \omega^2 \nonumber\]

Devemos converter a velocidade angular em radianos por segundo e calcular o momento de inércia antes de podermos descobrir\(KE_{rot}\) que a velocidade angular\(\omega\) é

\[\omega = \dfrac{300 \, rev}{1.00 \, min} \cdot \dfrac{2 \pi \, rad}{1 \, rev} \cdot \dfrac{1.00 \, min}{60.0 \, s} = 31.4 \dfrac{rad}{s}.\]

O momento de inércia de uma lâmina será o de uma haste fina girada em torno de sua extremidade, encontrada em [link]. O total\(I\) é quatro vezes esse momento de inércia, porque há quatro lâminas. Assim,

\[I = 4 \dfrac{Ml^2}{3} = 4 \times \dfrac{(50.0 \, kg)(4.00 \, kg)^2}{3} = 1067 \, kg \cdot m^2.\]

Ao entrar\(\omega\) e\(I\) entrar na expressão da energia cinética rotacional, obtém-se

\[KE_{rot} = 0.5(1067 \, kg \cdot m^2)(31.4 \, rad/s)^2\]

\[= 5.26 \times 10^5 \, J\]

Solução para (b)

A energia cinética translacional foi definida em Movimento Circular Uniforme e Gravitação. Inserindo os valores dados de massa e velocidade, obtemos

\[KE_{trans} = \dfrac{1}{2} mv^2 = (0.5)(1000 \, kg)(20.0 \, m/s)^2 = 2.00 \times 10^5 \, J.\]

Para comparar as energias cinéticas, tomamos a razão entre a energia cinética translacional e a energia cinética rotacional. Essa proporção é

\[ \dfrac{2.00 \times 10^5 \, J}{5.26 \times 10^5 \, J} = 0.380.\]

Solução para (c)

Na altura máxima, toda a energia cinética rotacional terá sido convertida em energia gravitacional. Para encontrar essa altura, igualamos essas duas energias:

\[KE_{rot} = PE_{grav}\]ou

\[\dfrac{1}{2} I\omega^2 = mgh.\]

Agora resolvemos\(h\) e substituímos valores conhecidos na equação resultante

\[h = \dfrac{\frac{1}{2}I \omega^2}{mg} = \dfrac{5.26 \times10^5 \, J}{(1000 \, kg)(9.80 \, m/s^2)} = 53.7 \, m\]

Discussão

A razão entre a energia translacional e a energia cinética rotacional é de apenas 0,380. Essa proporção nos diz que a maior parte da energia cinética do helicóptero está em suas pás giratórias, algo que você provavelmente não suspeitaria. A altura de 53,7 m até a qual o helicóptero poderia ser elevado com a energia cinética rotacional também é impressionante, enfatizando novamente a quantidade de energia cinética rotacional nas pás.

A conservação de energia inclui movimento rotacional, porque a energia cinética rotacional é outra forma de\(KE\). O Movimento Circular Uniforme e a Gravitação têm um tratamento detalhado da conservação de energia.

Qual é a espessura da sopa? Ou por que nem todos os objetos rolam ladeira abaixo no mesmo ritmo?

Um dos controles de qualidade em uma fábrica de sopa de tomate consiste em rolar latas cheias por uma rampa. Se rolarem muito rápido, a sopa fica muito fina. Por que latas de tamanho e massa idênticos deveriam rolar inclinadamente em taxas diferentes? E por que a sopa mais grossa deveria rolar mais devagar?

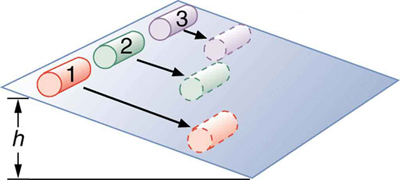
A maneira mais fácil de responder a essas perguntas é considerar a energia. Suponha que cada lata comece a descer a rampa do repouso. Cada lata partindo do repouso significa que cada uma começa com a mesma energia potencial gravitacional\(PE_{grav}\), que é totalmente convertida em\(KE\), desde que cada rolo sem escorregar. \(KE\)no entanto, pode assumir a forma de\(KE_{trans}\) ou\(KE_{rot}\), e o total\(KE\) é a soma dos dois. Se uma lata desce por uma rampa, ela coloca parte de sua energia em rotação, deixando menos para translação. Assim, a lata fica mais lenta do que se deslizasse para baixo. Além disso, a sopa fina não gira, enquanto a sopa grossa sim, porque gruda na lata. A sopa grossa, portanto, coloca mais energia potencial gravitacional original da lata em rotação do que a sopa fina, e a lata rola mais lentamente, como visto na Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): Três latas de sopa com massas idênticas descem uma inclinação. A primeira lata tem um revestimento de baixo atrito e não rola, mas apenas desliza na inclinação. Ele vence porque converte todo o seu PE em KE translacional. A segunda e a terceira latas rolam pela inclinação sem escorregar. A segunda lata contém sopa fina e vem em segundo porque parte de seu PE inicial gira a lata (mas não a sopa fina). A terceira lata contém sopa grossa. Ele vem em terceiro porque a sopa gira junto com a lata, absorvendo ainda mais do PE inicial para KE rotacional, deixando menos para KE translacional.

Supondo que não haja perdas devido ao atrito, há apenas uma força trabalhando: a gravidade. Portanto, o trabalho total realizado é a mudança na energia cinética. Quando as latas começam a se mover, a energia potencial está se transformando em energia cinética. A conservação da energia dá

\[PE_i = KE_f.\]

Mais especificamente,

\[PE_{grav} = KE_{trans} + KE_{rot}\]ou

\[mgh = \dfrac{1}{2}mv^2 + \dfrac{1}{2}I\omega^2.\]

Então, a inicial\(mgh\) é dividida entre energia cinética translacional e energia cinética rotacional; e quanto maior\(I\), menos energia entra na tradução. Se a lata deslizar para baixo sem atrito,\(\omega = 0\) toda a energia vai para a translação; assim, a lata vai mais rápido.

EXPERIÊNCIA PARA LEVAR PARA CASA

Localize várias latas, cada uma contendo diferentes tipos de alimentos. Primeiro, preveja qual pode vencer a corrida em um plano inclinado e explique o porquê. Veja se sua previsão está correta. Você também pode fazer esse experimento coletando vários recipientes cilíndricos vazios do mesmo tamanho e enchendo-os com materiais diferentes, como areia úmida ou seca.

Exemplo\(\PageIndex{3}\): Calculating the Speed of a Cylinder Rolling Down an Incline

Calcule a velocidade final de um cilindro sólido que desce por uma inclinação de 2,00 m de altura. O cilindro parte do repouso, tem uma massa de 0,750 kg e um raio de 4,00 cm.

Estratégia

Podemos resolver a velocidade final usando a conservação de energia, mas devemos primeiro expressar quantidades rotacionais em termos de quantidades translacionais para acabar sendo a única incógnita.

Solução

A conservação de energia para esta situação é escrita conforme descrito acima:

\[mgh = \dfrac{1}{2}mv^2 + \dfrac{1}{2}I\omega^2.\]

Antes de resolvermos\(v\), precisamos obter uma expressão para\(I\) de [link]. Como\(v\) e\(\omega\) estão relacionados (observe aqui que o cilindro está rolando sem escorregar), também devemos substituir a relação\(\omega = v/R\) na expressão. Essas substituições rendem

\[mgh = \dfrac{1}{2}mv^2 + \dfrac{1}{2}\left(\dfrac{1}{2}mR^2\right)\left(\dfrac{v^2}{R^2}\right).\]

Curiosamente, o raio\(R\) e a massa do cilindro se\(m\) cancelam, produzindo

\[gh = \dfrac{1}{2}v^2 + \dfrac{1}{4}v^2 = \dfrac{3}{4}v^2.\]

Resolvendo algebricamente, a equação para a velocidade final\(v\) fornece

\[v = \left(\dfrac{4gh}{3}\right)^{1/2}.\]

Substituir valores conhecidos na expressão resultante gera

\[v = \left[\dfrac{4(9.80 \, m/s^2)(2.00 \, m)}{3} \right]^{1/2} = 5.11 \, m/s.\]

Discussão

Como\(m\) e\(R\) cancele, o resultado\(v = (\frac{4}{3}gh)^{1/2}\) é válido para qualquer cilindro sólido, o que implica que todos os cilindros sólidos rolarão para baixo em uma inclinação na mesma taxa, independentemente de suas massas e tamanhos. (Rolar cilindros em declives é o que Galileu realmente fez para mostrar que os objetos caem na mesma taxa, independentemente da massa.) Observe que se o cilindro deslizasse sem atrito pela inclinação sem rolar, toda a energia potencial gravitacional entraria em energia cinética translacional. Assim,\(\frac{1}{2}mv^2 = mgh\)\(v = (2gh)^{1/2}, which is 22% greater than \((4gh/3)^{1/2}\) e. Ou seja, o cilindro iria mais rápido na parte inferior.

Exercício\(\PageIndex{1}\): Analogy of Rotational and Translational Kinetic Energy

A energia cinética rotacional é completamente análoga à energia cinética translacional? Quais, se houver, são suas diferenças? Dê um exemplo de cada tipo de energia cinética.

Solução

Sim, a energia cinética rotacional e translacional são análogas exatas. Ambos são a energia do movimento envolvida com o movimento coordenado (não aleatório) da massa em relação a algum quadro de referência. A única diferença entre a energia cinética rotacional e translacional é que o translacional é o movimento em linha reta, enquanto o rotacional não é. Um exemplo de energia cinética e translacional é encontrado em um pneu de bicicleta enquanto é percorrido por uma ciclovia. O movimento rotacional do pneu significa que ele tem energia cinética rotacional, enquanto o movimento da bicicleta ao longo do caminho significa que o pneu também tem energia cinética translacional. Se você levantasse a roda dianteira da bicicleta e girasse enquanto a bicicleta está parada, a roda teria apenas energia cinética rotacional em relação à Terra.

Resumo

• A energia cinética rotacional\(KE_{rot} \) para um objeto com um momento de inércia\(I\) e uma velocidade angular\(\omega\) é dada por

\[KE_{rot} = \dfrac{1}{2}I\omega^2.\]

• Os helicópteros armazenam grandes quantidades de energia cinética rotacional em suas pás. Essa energia deve ser colocada nas pás antes da decolagem e mantida até o final do voo. Os motores não têm potência suficiente para simultaneamente fornecer sustentação e colocar energia rotacional significativa nas pás.
• O trabalho e a energia no movimento rotacional são completamente análogos ao trabalho e à energia no movimento translacional.
• A equação para o teorema da energia de trabalho para o movimento rotacional é,\[net \, W = \dfrac{1}{2}I \omega^2 - \dfrac{1}{2}I \omega_0^2.\]

Glossário

teorema da energia do trabalho

se uma ou mais forças externas atuam sobre um objeto rígido, fazendo com que sua energia cinética mude de\(KE_1\) para\(KE_2\), então o trabalho\(W\) realizado pela força líquida é igual à mudança na energia cinética

energia cinética rotacional

a energia cinética devido à rotação de um objeto. Isso faz parte de sua energia cinética total