Skip to main content
Global

9.4: Aplicações da estática, incluindo estratégias de resolução de problemas

  1. Last updated
  2. Save as PDF
  • Page ID
    194986

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Discuta as aplicações da Estática na vida real.
    • Exponha e discuta várias estratégias de resolução de problemas em Estática.

    A estática pode ser aplicada a uma variedade de situações, desde levantar uma ponte levadiça até má postura e tensão nas costas. Começamos com uma discussão sobre estratégias de resolução de problemas usadas especificamente para estática. Como a estática é um caso especial das leis de Newton, tanto as estratégias gerais de resolução de problemas quanto as estratégias especiais para as leis de Newton, discutidas em Estratégias de Solução de Problemas, ainda se aplicam.

    Estratégia de resolução de problemas: situações de equilíbrio estático

    1. O primeiro passo é determinar se o sistema está ou não em equilíbrio estático. Essa condição é sempre o caso quando a aceleração do sistema é zero e a rotação acelerada não ocorre.
    2. É particularmente importante desenhar um diagrama corporal livre para o sistema de interesse. Identifique cuidadosamente todas as forças e observe suas magnitudes, direções e pontos de aplicação relativos sempre que eles forem conhecidos.
    3. Resolva o problema aplicando uma ou ambas as condições de equilíbrio (representadas pelas equações)\(net \, F = 0\) e\(net \, \tau = 0 \), dependendo da lista de fatores conhecidos e desconhecidos. Se a segunda condição estiver envolvida, escolha o ponto de articulação para simplificar a solução. Qualquer ponto de articulação pode ser escolhido, mas os mais úteis fazem com que torques por forças desconhecidas sejam zero. (O torque é zero se a força for aplicada no pivô (então\(r = 0\)) ou ao longo de uma linha que passa pelo ponto de articulação (então\\ theta = 0\)). Sempre escolha um sistema de coordenadas conveniente para projetar forças.
    4. Verifique a solução para ver se ela é razoável examinando a magnitude, a direção e as unidades da resposta. A importância dessa última etapa nunca diminui, embora em aplicações desconhecidas, geralmente seja mais difícil julgar a razoabilidade. Esses julgamentos se tornam progressivamente mais fáceis com a experiência.

    Agora, vamos aplicar essa estratégia de resolução de problemas para o salto com vara mostrado nas três figuras abaixo. O poste é uniforme e tem uma massa de 5,00 kg. Na Figura\(\PageIndex{1}\), o cg do poste fica a meio caminho entre as mãos do saltador. Parece razoável que a força exercida por cada mão seja igual à metade do peso do poste, ou 24,5 N. Isso obviamente satisfaz a primeira condição de equilíbrio\((net \, F = 0)\). A segunda condição também\((net \, \tau = 0)\) é satisfeita, como podemos ver ao escolher o cg como ponto de articulação. O peso não exerce torque em torno de um ponto de articulação localizado no cg, pois é aplicado nesse ponto e seu braço de alavanca é zero. As forças iguais exercidas pelas mãos são equidistantes do pivô escolhido e, portanto, exercem torques iguais e opostos.

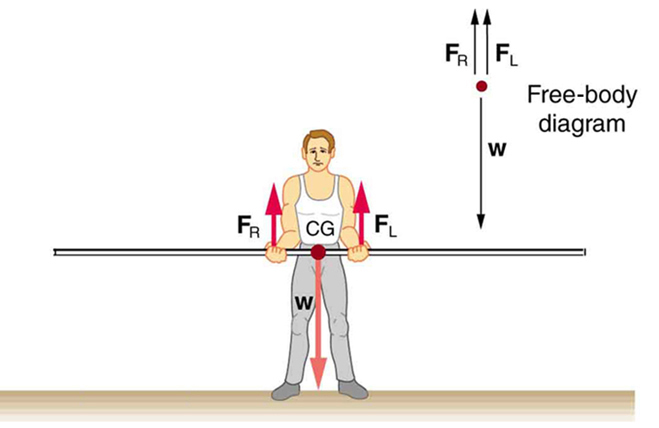
    Um saltador com vara está parado no chão segurando um poste com as duas mãos. O centro de gravidade do poste está entre as mãos do saltador com vara e está próximo à mão direita do homem. O peso W é mostrado como uma seta para baixo em direção ao centro de gravidade. As reações F sub R e F sub L das mãos do homem são mostradas com vetores na direção ascendente. Um diagrama de corpo livre da situação é mostrado no canto superior direito da figura.
    Figura\(\PageIndex{1}\): Um saltador com vara segura um poste horizontalmente com as duas mãos.

    Argumentos semelhantes são válidos para outros sistemas em que forças de apoio são exercidas simetricamente sobre o cg. Por exemplo, cada uma das quatro pernas de uma mesa uniforme suporta um quarto de seu peso. Na Figura\(\PageIndex{2}\), é mostrado um saltador com vara segurando um poste com seu cg a meio caminho entre as mãos. Cada mão exerce uma força igual à metade do peso do bastão\(F_r = F_L = w/2\). (b) O salto com vara move o mastro para a esquerda, e as forças que as mãos exercem não são mais iguais. Veja a Figura. Se o poste for segurado com o cg à esquerda da pessoa, ele deverá empurrar para baixo com a mão direita e para cima com a esquerda. As forças que ele exerce são maiores aqui porque estão em direções opostas e o cg está a uma longa distância de ambas as mãos.

    Observações semelhantes podem ser feitas usando um medidor mantido em diferentes locais ao longo de seu comprimento.

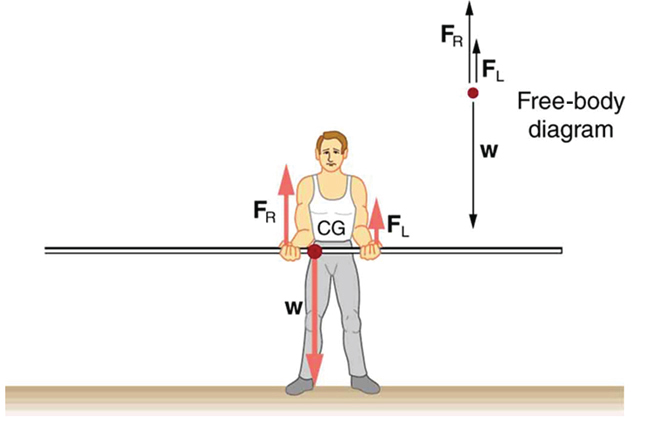
    Um saltador com vara está parado no chão segurando um poste com as duas mãos. O centro de gravidade do poste está entre as mãos do saltador com vara e está próximo à mão direita do homem. O peso W é mostrado como uma seta para baixo em direção ao centro de gravidade. As reações F sub R e F sub L das mãos do homem são mostradas com vetores na direção ascendente. Um diagrama de corpo livre da situação é mostrado no canto superior direito da figura.
    Figura\(\PageIndex{2}\): Um saltador com vara está segurando um poste horizontalmente com as duas mãos. O centro de gravidade está próximo à sua mão direita.
    Um saltador com vara está parado no chão segurando um poste de um lado com as duas mãos. O centro de gravidade do poste está à esquerda do salto com vara. O peso W é mostrado como uma seta para baixo no centro de gravidade. A reação F sub R é mostrada com um vetor apontando para baixo da mão direita do homem e F sub L é mostrada com um vetor na direção ascendente na localização da mão esquerda do homem. Um diagrama de corpo livre da situação é mostrado no canto superior direito da figura.
    Figura\(\PageIndex{3}\): Um saltador com vara está segurando um poste horizontalmente com as duas mãos. O centro de gravidade está no lado esquerdo do cofre.

    Se o salto com vara segurar o poste conforme mostrado na Figura, a situação não é tão simples. A força total que ele exerce ainda é igual ao peso do poste, mas não é dividida uniformemente entre suas mãos. (Se\(F_L = F_R \) sim, então os torques sobre o cg não seriam iguais, pois os braços da alavanca são diferentes.) Logicamente, a mão direita deve suportar mais peso, pois está mais próxima do GC. Na verdade, se a mão direita for movida diretamente sob o cg, ela suportará todo o peso. Essa situação é exatamente análoga a duas pessoas carregando uma carga; a mais próxima do GC carrega mais peso. Encontrando as forças\(F_L\) e\(F_R\) é simples, como mostra o próximo exemplo.

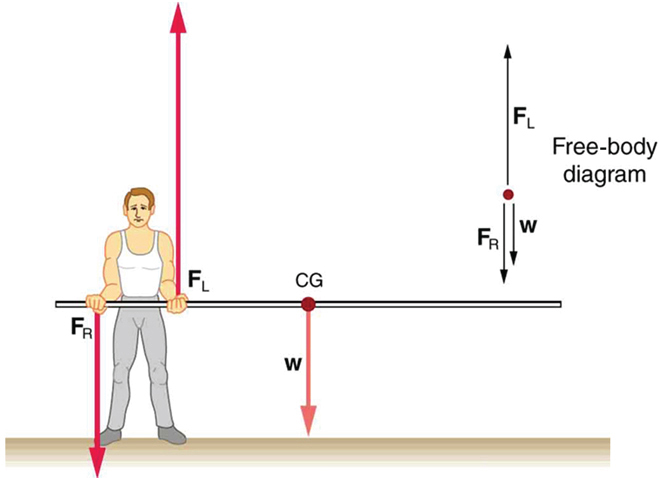
    Se o salto com vara segurar o mastro próximo ao final do poste (Figura), a direção da força aplicada pela mão direita do saltador inverte sua direção.

    Exemplo \(\PageIndex{1}\): What Force Is Needed to Support a Weight Held Near Its CG?

    Para a situação mostrada na Figura, calcule: (a)\(F_R\), a força exercida pela mão direita e (b)\(F_L\), a força exercida pela mão esquerda. As mãos estão separadas por 0,900 m e o cg do poste está a 0,600 m da mão esquerda.

    Estratégia

    A figura inclui um diagrama de corpo livre para o poste, o sistema de interesse. Não há informações suficientes para usar a primeira condição de equilíbrio\((net \, F = 0)\), pois duas das três forças são desconhecidas e as forças da mão não podem ser consideradas iguais neste caso. Há informações suficientes para usar a segunda condição de equilíbrio\((net \, \tau = 0)\) se o ponto de articulação for escolhido para estar em qualquer uma das mãos, tornando o torque dessa mão zero. Optamos por localizar o pivô na mão esquerda nessa parte do problema, para eliminar o torque da mão esquerda.

    Solução para (a)

    Agora existem apenas dois torques diferentes de zero, os da força gravitacional\((\tau_W)\) e do empurrão ou puxão da mão direita\((\tau_R)\). Declarando a segunda condição em termos de torques no sentido horário e anti-horário,

    \[net \, \tau_{CW} = -net \, \tau_{CCW}.\]

    ou a soma algébrica dos torques é zero.

    Aqui está\[\tau_R = -\tau_W\]

    já que o peso do poste cria um torque no sentido anti-horário e a mão direita contra-ataca com um toque no sentido horário. Usando a definição de torque\(\tau = rF \, sin \, \theta\), observando que\(\theta = 90^o\), e substituindo valores conhecidos, obtemos

    \[(0.900 \, m)(F_R) = (0.600 \, m)(mg).\]Assim,

    \[F_R = (0.667)(5.00 \, kg)(9.80 \, m/s^2)\]\[=32.7 \, N.\]

    Solução para (b)

    A primeira condição para o equilíbrio é baseada no diagrama de corpo livre na figura. Isso implica que, pela segunda lei de Newton:

    \[F_L + F_R - mg = 0\]

    A partir disso, podemos concluir\[F_L + F_R = w = mg\]

    Resolvendo para\(F_L\), obtemos

    \[F_L = mg - F_R\]

    \] = mg - 43,7\, N\]

    \[= (5.00 \, kg)(9.80 \, m/s^2) - 32.7 \, N\]

    \[= 16.3 \, N\]

    Discussão

    \(F_L\)é visto como exatamente a metade\(F_R\), como poderíamos ter adivinhado, uma vez que\(F_L\) é aplicado duas vezes mais longe de cg do que\(F_R\).

    Se o salto com vara segurar o poste como faria no início de uma corrida, mostrado na Figura, as forças mudam novamente. Ambos são consideravelmente maiores e uma força inverte a direção.

    Experiência para levar para casa

    • Este é um experimento para realizar enquanto estiver em um ônibus ou trem. Fique de frente para o lado. Como você move seu corpo para reajustar a distribuição de sua massa à medida que o ônibus acelera e desacelera? Agora fique voltado para a frente. Como você move seu corpo para reajustar a distribuição de sua massa à medida que o ônibus acelera e desacelera? Por que é mais fácil e seguro ficar de costas para os lados do que para frente? Nota: Para sua segurança (e das pessoas ao seu redor), certifique-se de segurar algo enquanto realiza esta atividade!

    Explorações PhET: Balancing Act

    Brinque com objetos em uma oscilação para aprender sobre equilíbrio. Teste o que você aprendeu experimentando o jogo Balance Challenge.

    Figura\(\PageIndex{4}\): Balancing Act

    Resumo

    • A estática pode ser aplicada a uma variedade de situações, desde levantar uma ponte levadiça até má postura e tensão nas costas. Discutimos as estratégias de resolução de problemas especificamente úteis para estática. A estática é um caso especial das leis de Newton, tanto as estratégias gerais de resolução de problemas quanto as estratégias especiais para as leis de Newton, discutidas em Estratégias de Solução de Problemas, ainda se aplicam.
     

    Glossário

    equilíbrio estático
    equilíbrio em que a aceleração do sistema é zero e a rotação acelerada não ocorre