9.5: Máquinas simples

Last updated
Save as PDF

Page ID: 194984

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Descreva diferentes máquinas simples.
Calcule a vantagem mecânica.

Máquinas simples são dispositivos que podem ser usados para multiplicar ou aumentar uma força que aplicamos — geralmente à custa de uma distância pela qual aplicamos a força. A palavra para “máquina” vem da palavra grega que significa “ajudar a tornar as coisas mais fáceis”. Alavancas, engrenagens, polias, cunhas e parafusos são alguns exemplos de máquinas. A energia ainda é conservada para esses dispositivos porque uma máquina não pode fazer mais trabalho do que a energia investida nela. No entanto, as máquinas podem reduzir a força de entrada necessária para realizar o trabalho. A relação entre as magnitudes da força de saída e de entrada para qualquer máquina simples é chamada de vantagem mecânica (MA).

\[MA = \dfrac{F_o}{F_i}\]

Uma das máquinas mais simples é a alavanca, que é uma barra rígida girada em um local fixo chamado ponto de apoio. Os torques estão envolvidos nas alavancas, pois há rotação em torno de um ponto de articulação. As distâncias do pivô físico da alavanca são cruciais, e podemos obter uma expressão útil para o MA em termos dessas distâncias.

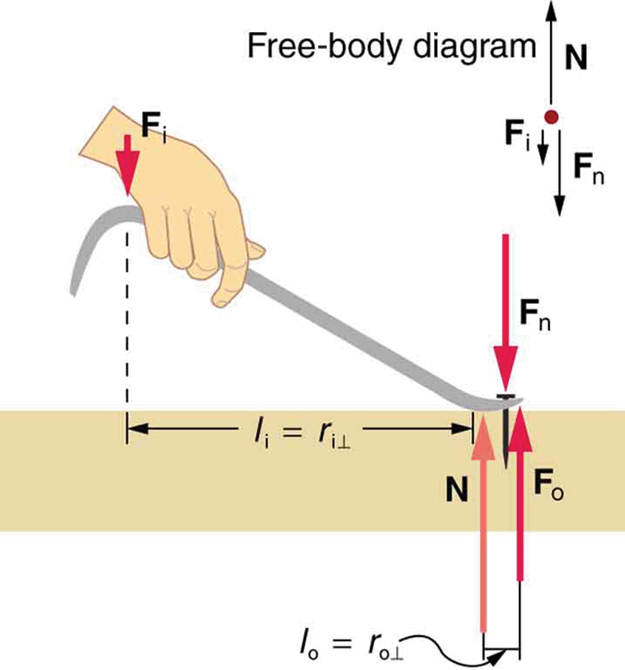
Há um prego em uma prancha de madeira. Um extrator de unhas está sendo usado para puxar o prego para fora da prancha. Uma mão está aplicando a força F sub I para baixo na alça do extrator de unhas. A parte superior do prego exerce uma força F sub N para baixo no extrator. No ponto em que o extrator de pregos toca a prancha, a reação da força superficial N é aplicada. Na parte superior da figura, um diagrama de corpo livre é mostrado. — Figura\(\PageIndex{1}\): Um extrator de unhas é uma alavanca com uma grande vantagem mecânica. As forças externas no extrator de unhas são representadas por setas sólidas. A força que o extrator de unhas aplica ao prego não\((F_o)\) é uma força no extrator de unhas. A força de reação que o prego exerce sobre o extrator\((F_n)\) é uma força externa e é igual e oposta\(F_o\). Os braços de alavanca perpendiculares das forças de entrada\(l_i\) e saída são\(l_o\) e.

A figura mostra um tipo de alavanca usado como extrator de unhas. Pés de cabra, gangorras e outras alavancas semelhantes são todas análogas a esta\(F_i\) é a força de entrada e\(F_o\) a força de saída. Existem três forças verticais atuando no extrator de pregos (o sistema de interesse) - essas são\(F_i\)\(F_o\), e\(N.\)\(F_n\) é a força de reação de volta ao sistema, igual e oposta\(F_o\) a. (observe que isso não\(F_o\) é uma força no sistema.) \(N\)é a força normal sobre a alavanca e seu torque é zero, pois é exercido no pivô. Os torques devidos\(F_i\) e\(F_n\) devem ser iguais entre si se o prego não estiver se movendo, para satisfazer a segunda condição de equilíbrio\((net \, \tau = 0)\). (Para que o prego realmente se mova, o torque devido\(F_i\) deve ser ligeiramente maior do que o torque devido\(F_n\) a.) Conseqüentemente,

\[l_iF_i = l_oF_o\]onde\(l_i\) e\(l_o\) são as distâncias de onde as forças de entrada e saída são aplicadas ao pivô, conforme mostrado na figura. Reorganizar a última equação dá\[ \dfrac{F_o}{F_i} = \dfrac{l_i}{l_o}.\] O que mais nos interessa aqui é que a magnitude da força exercida pelo puxador de pregos,\(F_o\), é muito maior do que a magnitude da força de entrada aplicada ao extrator na outra extremidade,\(F_i\). Para o extrator de unhas,\[MA = \dfrac{F_o}{F_i} = \dfrac{l_i}{l_o}.\]

Essa equação é verdadeira para alavancas em geral. Para o extrator de unhas, o MA é certamente maior que um. Quanto maior a alça do extrator de unhas, maior a força que você pode exercer com ele.

Dois outros tipos de alavancas que diferem ligeiramente do extrator de pregos são um carrinho de mão e uma pá, mostrados na Figura. Todos esses tipos de alavanca são semelhantes, pois apenas três forças estão envolvidas - a força de entrada, a força de saída e a força no pivô - e, portanto, seus MAs são dados por\(MA = \frac{F_o}{F_i} \) e\(MA = \frac{d_1}{d_2}\), com distâncias sendo medidas em relação ao pivô físico. O carrinho de mão e a pá diferem do extrator de pregos porque as forças de entrada e saída estão no mesmo lado do pivô.

No caso do carrinho de mão, a força ou carga de saída está entre o pivô (o eixo da roda) e a força de entrada ou aplicada. No caso da pá, a força de entrada está entre o pivô (na extremidade da alça) e a carga, mas o braço da alavanca de entrada é mais curto que o braço da alavanca de saída. Nesse caso, o MA é menor que um.

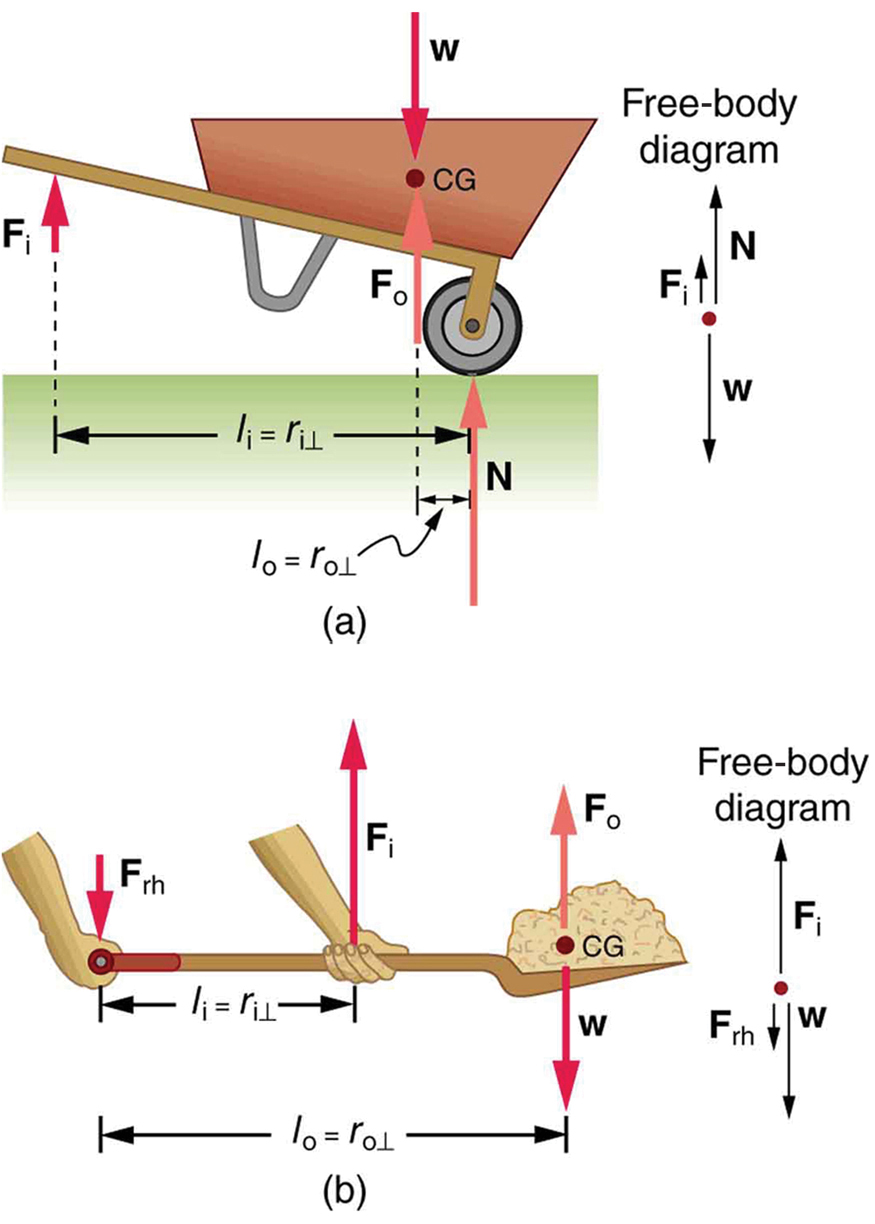
É mostrado um carrinho de mão no qual a força de entrada F sub I é mostrada como um vetor na direção vertical para cima abaixo da alça do carrinho de mão. O peso do carrinho de mão está voltado para baixo no centro de gravidade. A reação normal do solo está atuando ao volante na direção ascendente. A distância perpendicular entre a reação normal e a força de entrada F sub I é rotulada como R sub I e a distância entre a força de saída F sub O e a reação normal é rotulada como R sub O. Na figura b, um homem está segurando uma pá nas mãos. Uma mão está em uma extremidade da alça e a outra mão está segurando a pá no meio. O centro de gravidade da pá está em sua extremidade plana. O peso da pá está atuando no centro de gravidade. A força de entrada está atuando na mão no meio na direção ascendente e a extremidade da pá está atuando como pivô. Um diagrama de corpo livre também é mostrado no lado direito da figura. — Figura\(\PageIndex{2}\): (a) No caso do carrinho de mão, a força ou carga de saída está entre o pivô e a força de entrada. O pivô é o eixo da roda. Aqui, a força de saída é maior que a força de entrada. Assim, um carrinho de mão permite que você levante cargas muito mais pesadas do que com o corpo sozinho. (b) No caso da pá, a força de entrada está entre o pivô e a carga, mas o braço da alavanca de entrada é mais curto que o braço da alavanca de saída. O pivô está na alça segurada pela mão direita. Aqui, a força de saída (suportando a carga da pá) é menor que a força de entrada (da mão mais próxima da carga), porque a entrada é exercida mais perto do pivô do que a saída.

Exemplo\(\PageIndex{1}\): What is the Advantage for the Wheelbarrow?

No carrinho de mão da Figura, a carga tem um braço de alavanca perpendicular de 7,50 cm, enquanto as mãos têm um braço de alavanca perpendicular de 1,02 m. (a) Que força ascendente você deve exercer para apoiar o carrinho de mão e sua carga se sua massa combinada for de 45,0 kg? (b) Que força o carrinho de mão exerce no chão?

Estratégia

Aqui, usamos o conceito de vantagem mecânica.

Solução

(a) Neste caso,\(\frac{F_o}{F_i} = \frac{l_i}{l_o}\) torna-se\[F_i = F_o\dfrac{l_o}{l_i},\]

A adição de valores a essa equação gera

\[F_i = (45.0 \, kg)(9.80 \, m/s^2)\dfrac{0.075\space m}{1.02 \, m} = 32.4 \, N.\]

O diagrama de corpo livre (veja a Figura) fornece a seguinte força normal:\[F_i = + N = W.\] Portanto,

\[N = (45.0 \, kg)(9.80 \, m/s^2) - 32.4 \, N = 409 \, N.\]

\(N\)é a força normal atuando na roda; pela terceira lei de Newton, a força que a roda exerce no solo é\(409 \, N\).

Discussão

Uma alça ainda mais longa reduziria a força necessária para levantar a carga. O MA aqui é\(MA = 1.01/0.0750 = 13.6\)

Outra máquina muito simples é o plano inclinado. Empurrar um carrinho para cima de um avião é mais fácil do que levantar o mesmo carrinho diretamente até o topo usando uma escada, porque a força aplicada é menor. No entanto, o trabalho realizado em ambos os casos (supondo que o trabalho realizado por atrito seja insignificante) é o mesmo. As pistas ou rampas inclinadas provavelmente foram usadas durante a construção das pirâmides egípcias para mover grandes blocos de pedra até o topo.

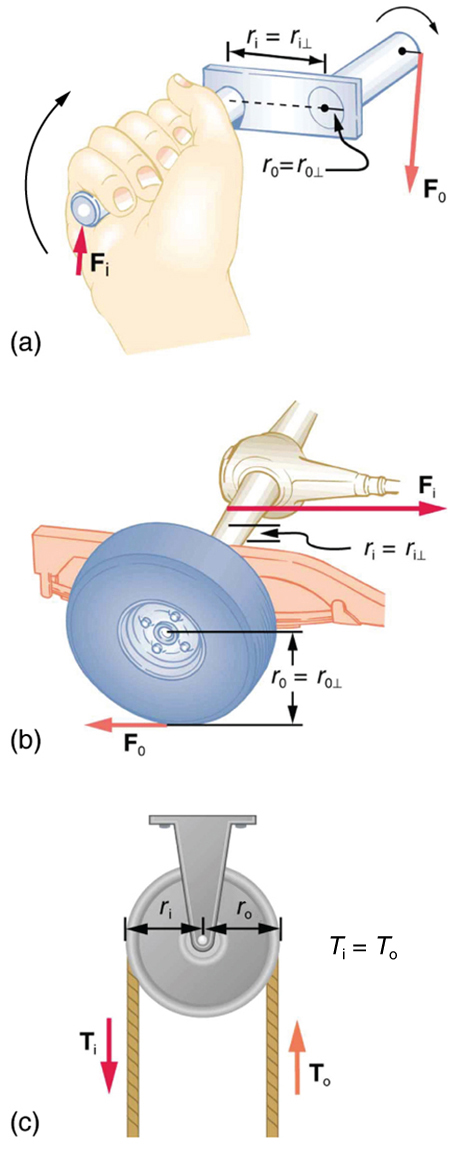
Uma manivela é uma alavanca que pode ser girada em\(360^o\) torno de seu pivô, conforme mostrado na Figura. Essa máquina pode não parecer uma alavanca, mas a física de suas ações permanece a mesma. O MA de uma manivela é simplesmente a proporção dos raios\(r_i/r_o\). Rodas e engrenagens também têm essa expressão simples para seus MAs. O MA pode ser maior que 1, como é para a manivela, ou menor que 1, como é para o eixo simplificado do carro que aciona as rodas, conforme mostrado. Se o raio do eixo for\(2.0 \, cm\) e o raio da roda for\(24.0 \, cm\), então\(MA = 2.0/24.0 = 0.083\) o eixo teria que exercer uma força de\(12,000 \, N\) sobre a roda para permitir que ela exerça uma força de\(1000 \, N\) no solo.

Na figura a, é mostrada uma alavanca de manivela na qual uma mão está na alça da manivela. A força de saída F sub O está na base da alavanca e a força de entrada F sub I está na alça da alavanca. A distância entre a força de entrada e a força de saída é rotulada como R sub I. Na figura b, um eixo simplificado do carro é mostrado. A força de entrada é mostrada como um vetor F sub I no eixo em direção à direita. A força de saída é mostrada no ponto de contato da roda com o solo voltado para a esquerda. A distância entre a força de saída e o ponto de articulação é rotulada como R sub O. Na figura c, a corda sobre a polia é mostrada. A força de entrada é mostrada como uma seta para baixo na parte esquerda da corda. A força de saída está atuando na parte direita da corda. O centro da polia é o ponto de articulação. As distâncias das duas forças do pivô são R sub I e R sub O, respectivamente. — Figura\(\PageIndex{3}\): (a) Uma manivela é um tipo de alavanca que pode ser girada em\(360^o\) torno de seu pivô. As manivelas geralmente são projetadas para ter uma grande MA. (b) Um eixo de automóvel simplificado aciona uma roda, que tem um diâmetro muito maior do que o eixo. O MA é menor que 1. (c) Uma polia comum é usada para levantar uma carga pesada. A polia muda a direção da força\(T\) exercida pelo cabo sem alterar sua magnitude. Portanto, esta máquina tem um MA de 1.

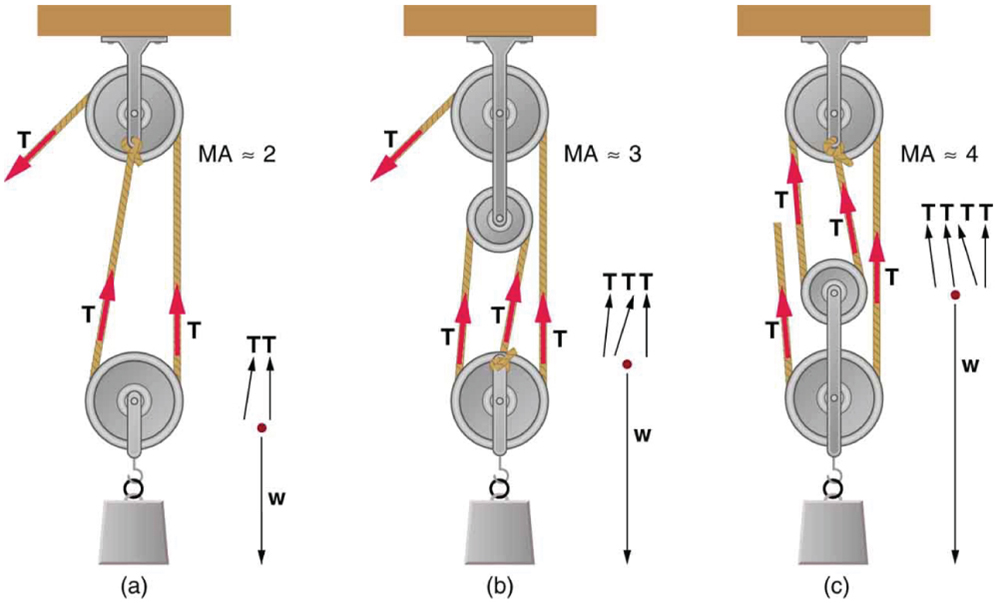
Uma polia comum tem uma MA de 1; ela muda apenas a direção da força e não sua magnitude. Combinações de polias, como as ilustradas na Figura, são usadas para multiplicar a força. Se as polias estiverem livres de atrito, a saída de força é aproximadamente um múltiplo integral da tensão no cabo. O número de cabos puxados diretamente para cima no sistema de interesse, conforme ilustrado nas figuras abaixo, é aproximadamente a MA do sistema de polias. Como cada acessório aplica uma força externa aproximadamente na mesma direção que os outros, eles se somam, produzindo uma força total que é quase um múltiplo integral da força de entrada\(T\).

Na figura a, uma corda sobre duas polias é mostrada. Uma polia é fixada no teto e a outra está pendurada na corda. Um peso está pendurado na segunda polia. As tensões T são mostradas nas duas partes da polia suspensa e na extremidade livre do cabo. A vantagem mecânica do sistema é duas. Na figura b, um conjunto de três polias é mostrado. Uma polia é fixada no teto com outra polia abaixo dela. A terceira polia está pendurada na corda com um peso pendurado nela. As tensões na corda são mostradas como vetores na corda e na extremidade da corda. Na figura c, é mostrado um conjunto de três polias. Uma das polias está fixada no teto. Duas polias conectadas estão penduradas em uma corda sobre a primeira polia. As direções das tensões estão marcadas nas cordas e na extremidade da corda. — Figura 9.6.4. (a) A combinação de polias é usada para multiplicar a força. A força é um múltiplo integral da tensão se as polias não tiverem atrito. Esse sistema de polias tem dois cabos conectados à sua carga, aplicando assim uma força de aproximadamente\(2T\). Esta máquina tem\(MA \approx 2\). (b) Três polias são usadas para levantar uma carga de tal forma que a vantagem mecânica seja de cerca de 3. Efetivamente, existem três cabos conectados à carga. (c) Este sistema de polias aplica uma força de\(4T\), de modo que tem\(MA \approx 4\). Efetivamente, quatro cabos estão acionando o sistema de interesse.

Resumo

Máquinas simples são dispositivos que podem ser usados para multiplicar ou aumentar uma força que aplicamos — geralmente à custa de uma distância pela qual temos que aplicar a força.
A relação entre as forças de saída e entrada para qualquer máquina simples é chamada de vantagem mecânica.
Algumas máquinas simples são a alavanca, o puxador de pregos, o carrinho de mão, a manivela, etc.

Glossário

vantagem mecânica: a relação entre as forças de saída e entrada para qualquer máquina simples