9.2: A segunda condição para o equilíbrio

Last updated
Save as PDF

Page ID: 194947

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Indique a segunda condição necessária para alcançar o equilíbrio.
Explique o torque e os fatores dos quais ele depende.
Descreva o papel do torque na mecânica rotacional.

Definição: Torque

A segunda condição necessária para alcançar o equilíbrio envolve evitar a rotação acelerada (mantendo uma velocidade angular constante). Um corpo ou sistema rotativo pode estar em equilíbrio se sua taxa de rotação for constante e permanecer inalterada pelas forças que atuam sobre ele. Para entender quais fatores afetam a rotação, vamos pensar no que acontece quando você abre uma porta comum girando-a em suas dobradiças.

Vários fatores familiares determinam o quão eficaz você é ao abrir a porta (Figura\(\PageIndex{1}\)). Em primeiro lugar, quanto maior a força, mais eficaz ela é em abrir a porta — obviamente, quanto mais você empurra, mais rapidamente a porta se abre. Além disso, o ponto em que você empurra é crucial. Se você aplicar sua força muito perto das dobradiças, a porta se abrirá lentamente, se for o caso. A maioria das pessoas ficou envergonhada ao cometer esse erro e esbarrar em uma porta quando ela não abriu tão rápido quanto o esperado. Finalmente, a direção na qual você empurra também é importante. A direção mais eficaz é perpendicular à porta — nós empurramos nessa direção quase instintivamente.

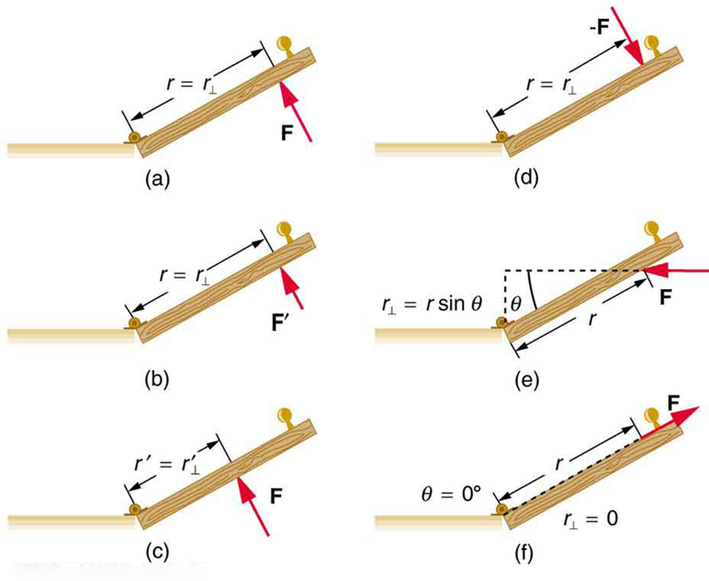
Na figura, seis vistas superiores de uma porta são mostradas. Na primeira figura, um vetor de força é mostrado na direção noroeste. A distância perpendicular da força do ponto de rotação é r. Na segunda figura, uma força é aplicada na direção oposta à mesma distância das dobradiças. Na terceira figura, uma força menor é aplicada no mesmo ponto. Na figura a seguir, uma força horizontal é aplicada no mesmo ponto. Nesse caso, a distância perpendicular das dobradiças é mostrada como r sin teta. Na figura a seguir, a força é aplicada a uma distância próxima às dobradiças. Na figura final, a força é mostrada ao longo da direção das dobradiças em direção à maçaneta da porta. — Figura\(\PageIndex{1}\): O torque é a eficácia de giro ou torção de uma força, ilustrada aqui para a rotação da porta em suas dobradiças (vista de cima). O torque tem magnitude e direção. (a) O torque anti-horário é produzido por essa força, o que significa que a porta girará no sentido anti-horário devido\(F\) a. Observe que\(r_{\perp}\) é a distância perpendicular do pivô da linha de ação da força. (b) Um torque menor no sentido anti-horário é produzido por uma força menor\(F'\) atuando à mesma distância das dobradiças (o ponto de articulação). (c) A mesma força que em (a) produz um torque menor no sentido anti-horário quando aplicada a uma distância menor das dobradiças. (d) A mesma força de (a), mas atuando na direção oposta, produz um torque no sentido horário. (e) Um torque menor no sentido anti-horário é produzido pela mesma força de magnitude atuando no mesmo ponto, mas em uma direção diferente. Aqui,\(\theta\) é menor que\(90^o\). (f) O torque é zero aqui, pois a força apenas puxa as dobradiças, não produzindo rotação. Nesse caso,\(\theta = 0^o\).

A magnitude, a direção e o ponto de aplicação da força são incorporados à definição da quantidade física chamada torque. O torque é o equivalente rotacional de uma força. É uma medida da eficácia de uma força em mudar ou acelerar uma rotação (alterando a velocidade angular ao longo de um período de tempo). Em forma de equação, a magnitude do torque é definida como

\[\tau = rF\, \sin \, \theta\]

onde\(\tau\) (a letra grega tau) é o símbolo do torque,\(r\) é a distância do ponto de articulação até o ponto em que a força\(F\) é aplicada, é a magnitude da força e\(\theta\) é o ângulo entre a força e o vetor direcionado do ponto de aplicação ao pivô ponto, como visto nas Figuras\(\PageIndex{1}\)\(\PageIndex{2}\) e.

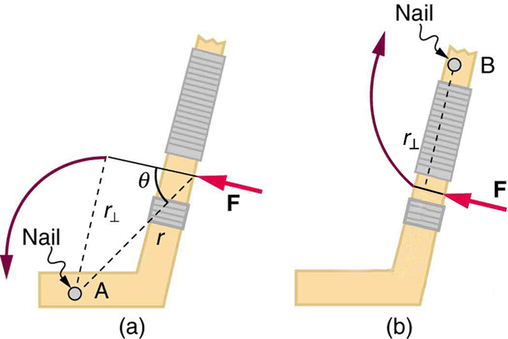
Na primeira parte da figura, um taco de hóquei é mostrado. Em um ponto A próximo ao fundo, um prego é fixado. Uma força é aplicada em um ponto próximo à alça do taco de hóquei. Um quarto de seta circular mostra que o manípulo gira no sentido anti-horário. A distância perpendicular entre o ponto de articulação e a direção do vetor de força é rotulada como r-perpendicular, e o ângulo entre a direção da força e a linha que une o pivô A ao ponto de aplicação da força é dado como teta. Na segunda parte da figura, o ponto de articulação está próximo ao topo do bastão e o ponto de aplicação da força é aproximadamente o mesmo da primeira parte da figura. Uma seta de um quarto de círculo para cima mostra que o manípulo gira no sentido horário. — Figura\(\PageIndex{2}\): Uma força aplicada a um objeto pode produzir um torque, que depende da localização do ponto de articulação. (a) Os três fatores\(r, \, F\) e\(\theta\) para o ponto de articulação A em um corpo são mostrados aqui -\(r\) é a distância do ponto de articulação escolhido até o ponto onde a força\(F\) é aplicada, e\(\theta\) é o ângulo entre\(F\) e o vetor direcionado do ponto de aplicação para o ponto de pivô. Se o objeto puder girar em torno do ponto A, ele girará no sentido anti-horário. Isso significa que o torque está no sentido anti-horário em relação ao pivô A. (b) Nesse caso, o ponto B é o ponto de articulação. O torque da força aplicada causará uma rotação no sentido horário em torno do ponto B e, portanto, é um torque no sentido horário em relação a B.

Uma expressão alternativa para torque é dada em termos do braço perpendicular da alavanca,\(r_{\perp}\) conforme mostrado nas Figuras\(\PageIndex{1}\) e\(\PageIndex{2}\), que é definido como

\[r_{\perp} = r \, \sin \, \theta\]

para que

\[\tau = r_{\perp}F.\]

O braço perpendicular da alavanca\(r_{\perp}\) é a menor distância do ponto de articulação até a linha ao longo da qual\(F\) atua; é mostrado como uma linha tracejada nas Figuras\(\PageIndex{1}\)\(\PageIndex{2}\) e. Observe que o segmento de linha que define a distância\(r_{\perp}\) é perpendicular a\(F\), como o próprio nome indica. Às vezes, é mais fácil encontrar ou visualizar\(r_{\perp}\) do que encontrar os dois\(r\)\(\theta\) e. Nesses casos, pode ser mais conveniente usá-lo\(\tau = r_{perp}F\) do que\(\tau = rF \, \sin \, \theta\) para torque, mas ambos são igualmente válidos.

A unidade de torque SI é newtons vezes metros, geralmente escrita como\(N \cdot m\). Por exemplo, se você empurrar perpendicularmente à porta com uma força de 40 N a uma distância de 0,800 m das dobradiças, você exerce um torque\(32 \, N \cdot m(0.800 \, m \times 40 \, N \times sin \, 90^o)\) em relação às dobradiças. Se você reduzir a força para 20 N, o torque será reduzido para\(16 \, N \cdot m\), e assim por diante.

O torque é sempre calculado com referência a algum ponto de articulação escolhido. Para a mesma força aplicada, uma escolha diferente para a localização do pivô fornecerá um valor diferente para o torque, pois ambos\(r\)\(\theta\) dependem da localização do pivô. Qualquer ponto em qualquer objeto pode ser escolhido para calcular o torque em torno desse ponto. Na verdade, o objeto pode não girar em torno do “ponto de articulação” escolhido.

Observe que, para rotação em um plano, o torque tem duas direções possíveis. O torque é no sentido horário ou anti-horário em relação ao ponto de articulação escolhido, conforme ilustrado para os pontos B e A, respectivamente, na Figura\(\PageIndex{2}\). Se o objeto puder girar em torno do ponto A, ele girará no sentido anti-horário, o que significa que o torque da força é mostrado no sentido anti-horário em relação a A. Mas se o objeto puder girar em torno do ponto B, ele girará no sentido horário, o que significa que o torque da força mostrada é no sentido horário em relação a B. Além disso, o a magnitude do torque é maior quando o braço da alavanca é maior.

Agora, a segunda condição necessária para alcançar o equilíbrio é que o torque externo líquido em um sistema seja zero. Um torque externo é aquele criado por uma força externa. Você pode escolher o ponto em torno do qual o torque é calculado. O ponto pode ser o ponto de articulação físico de um sistema ou qualquer outro ponto no espaço, mas deve ser o mesmo ponto para todos os torques. Se a segunda condição (torque externo líquido em um sistema é zero) for satisfeita para uma opção de ponto de articulação, ela também será válida para qualquer outra opção de ponto de articulação dentro ou fora do sistema de interesse. (Isso é verdade somente em um quadro de referência inercial.) A segunda condição necessária para alcançar o equilíbrio é declarada em forma de equação como

\[net \, \tau = 0\]

onde líquido significa total. Os torques, que estão em direções opostas, recebem sinais opostos. Uma convenção comum é chamar torques no sentido anti-horário (ccw) positivos e no sentido horário (cw) negativos.

Quando duas crianças equilibram uma gangorra, conforme mostrado na Figura\(\PageIndex{3}\), elas satisfazem as duas condições de equilíbrio. A maioria das pessoas tem uma intuição perfeita sobre gangorras, sabendo que a criança mais leve deve se sentar mais longe do pivô e que uma criança mais pesada pode manter uma mais leve do chão indefinidamente.

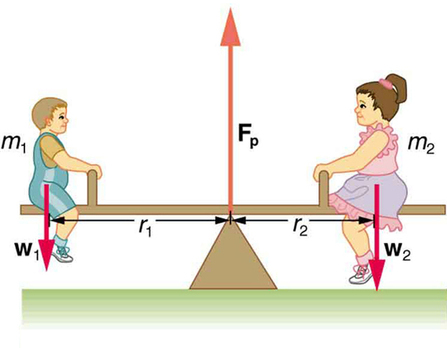
À direita do diagrama, há um longo retângulo marrom claro com um ponto preto sólido na extremidade direita. Abaixo do retângulo longo, há uma seta de duas pontas apontando para linhas verticais em cada extremidade do bloco rotulada com um d no centro. Abaixo da linha vertical esquerda, há uma seta vermelha apontando para cima chamada FA. À esquerda da linha vertical esquerda está uma seta vermelha apontando para a direita chamada FB. Acima do retângulo longo marrom-claro está um segmento de linha curta apontando para cima rotulado FI. Do topo da linha FI, há outra linha curta se movendo para a esquerda e rotulada FII. Há uma seta vermelha chamada FC apontando para cerca de 30 graus para baixo e para a direita para fechar o triângulo entre FI, FII e FC. O ângulo entre FII e FC é rotulado como teta. — Figura\(\PageIndex{3}\): Duas crianças balanceando uma gangorra satisfazem as duas condições de equilíbrio. A criança mais leve fica mais longe do pivô para criar um torque igual em magnitude ao da criança mais pesada.

Exemplo\(\PageIndex{1}\): She Saw Torques On A Seesaw

As duas crianças mostradas na Figura\(\PageIndex{3}\) estão balanceadas em uma gangorra de massa insignificante. (Essa suposição é feita para manter o exemplo simples — exemplos mais envolventes virão.) O primeiro filho tem uma massa de 26,0 kg e fica a 1,60 m do pivô.

Se a segunda criança tiver uma massa de 32,0 kg, a que distância ela está do pivô?
O que é\(F_p\) a força de apoio exercida pelo pivô?

Estratégia

Ambas as condições de equilíbrio devem ser satisfeitas. Na parte (a), somos solicitados a fornecer uma distância; portanto, a segunda condição (em relação aos torques) deve ser usada, já que a primeira (considerando apenas as forças) não tem distâncias nela. Para aplicar a segunda condição de equilíbrio, primeiro identificamos o sistema de interesse como a gangorra mais as duas crianças. Consideramos que o pivô de suporte é o ponto sobre o qual os torques são calculados. Em seguida, identificamos todas as forças externas que atuam no sistema.

Solução (a)

As três forças externas que atuam no sistema são os pesos das duas crianças e a força de apoio do pivô. Vamos examinar o torque produzido por cada um. O torque é definido como

\[\tau = rF \, \sin \, \theta. \nonumber\]

Aqui\(\theta = 90^o,\),\(sin \, \theta = 1\) para todas as três forças. Isso significa\(r_{\perp} = r\) para todos os três. Os torques exercidos pelas três forças são os primeiros,

\[\tau_1 = r_1w_1\nonumber\]

segundo,

\[\tau_2 = -r_2w_2\nonumber\]

e terceiro,

\[ \begin{align*} \tau_p &= r_pF_p \\[5pt] &= 0 \cdot F_p \\[5pt] &= 0. \end{align*}\]

Observe que um sinal de menos foi inserido na segunda equação porque esse torque é no sentido horário e, portanto, é negativo por convenção. Como\(F_p\) atua diretamente no ponto de articulação, a distância\(r_p\) é zero. Uma força atuando no pivô não pode causar uma rotação, assim como empurrar diretamente as dobradiças de uma porta não fará com que ela gire. Agora, a segunda condição para o equilíbrio é que a soma dos torques em ambas as crianças seja zero. Portanto

\[\tau_2 = -\tau_1,\nonumber\]

\[r_2w_2 = r_1w_1.\nonumber\]

O peso é a massa vezes a aceleração devido à gravidade. Entrando\(mg\) para\(w\), obtemos

\[r_2m_2g = r_1w_1g.\nonumber\]

Resolva isso para o desconhecido\(r_2\):

\[r_2 = r_1\dfrac{m_1}{m_2}.\nonumber\]

As quantidades no lado direito da equação são conhecidas; portanto,\(r_2\) é

\[ \begin{align*} r_2 &= (1.60 \, m)\dfrac{26.0 \, kg}{32.0 \, kg} \\[5pt] &= 1.30 \, m \end{align*}\]

Como esperado, a criança mais pesada deve se sentar mais perto do pivô (1,30 m versus 1,60 m) para equilibrar a gangorra.

Solução (b)

Essa parte pede uma força\(F_p\). A maneira mais fácil de encontrá-lo é usar a primeira condição para o equilíbrio, que é

\[net \, F = 0.\nonumber\]

As forças são todas verticais, então estamos lidando com um problema unidimensional ao longo do eixo vertical; portanto, a condição pode ser escrita como

\[net \, F_y = 0 \nonumber\]

onde novamente chamamos o eixo vertical de eixo y. Escolhendo para cima a direção positiva e usando sinais de mais e menos para indicar as direções das forças, vemos que

\[F_p - w_1 - w_2 = 0.\nonumber\]

Essa equação produz o que pode ter sido adivinhado no início:

\[F_p = w_1 + w_2. \nonumber\]

Portanto, o pivô fornece uma força de suporte igual ao peso total do sistema:

\[F_p = m_1g + m_2g. \nonumber\]

A inserção de valores conhecidos fornece

\[ \begin{align*} F_p &= (26.0 \, kg)(9.80 \, m/s^2) + (32.0 \, kg)(9.80 \, m/s^2) \\[5pt] &= 568 \, N. \end{align*}\]

Discussão

Os dois resultados fazem sentido intuitivo. A criança mais pesada fica mais perto do pivô. O pivô suporta o peso das duas crianças. A parte (b) também pode ser resolvida usando a segunda condição de equilíbrio, já que ambas as distâncias são conhecidas, mas somente se o ponto de articulação for escolhido para estar em algum lugar diferente da localização real do pivô da gangorra!

Vários aspectos do exemplo anterior têm implicações amplas. Primeiro, a escolha do pivô como o ponto em torno do qual os torques são calculados simplificou o problema. Como\(F_p\) é exercido no ponto de articulação, seu braço de alavanca é zero. Portanto, o torque exercido pela força de suporte\(F_p\) é zero em relação a esse ponto de articulação. A segunda condição para o equilíbrio é válida para qualquer opção de ponto de articulação e, portanto, escolhemos o ponto de articulação para simplificar a solução do problema.

Em segundo lugar, a aceleração devido à gravidade foi cancelada nesse problema e ficamos com uma proporção de massas. Isso nem sempre será o caso. Sempre insira as forças corretas — não avance para inserir alguma proporção de massas.

Terceiro, o peso de cada criança é distribuído por uma área da gangorra, mas tratamos os pesos como se cada força fosse exercida em um único ponto. Isso não é uma aproximação — as distâncias\(r_{\perp}\) e\(r_2\) são as distâncias até os pontos diretamente abaixo do centro de gravidade de cada criança. Como veremos na próxima seção, a massa e o peso de um sistema podem agir como se estivessem localizados em um único ponto.

Finalmente, observe que o conceito de torque tem uma importância além do equilíbrio estático. O torque desempenha o mesmo papel no movimento rotacional que a força desempenha no movimento linear. Examinaremos isso no próximo capítulo.

Experiência para levar para casa

Pegue um pedaço de argila de modelar e coloque-o sobre uma mesa, depois amasse um cilindro nele para que uma régua possa se equilibrar no lado redondo do cilindro enquanto tudo permanece imóvel. Coloque um centavo a 8 cm de distância do pivô. Onde você precisaria colocar dois centavos para equilibrar? Três centavos?

Resumo

A segunda condição garante que esses torques também sejam equilibrados. O torque é o equivalente rotacional de uma força na produção de uma rotação e\(\tau\) é definido como\[\tau = rF \, \sin \, \theta \nonumber\] onde\(r\) está o torque, é a distância do ponto de articulação até o ponto onde a força é aplicada,\(F\) é a magnitude da força e\(\theta\) é o ângulo entre\(F\) e o vetor direcionado do ponto onde a força atua até o ponto de articulação. O braço da alavanca perpendicular\(r_{\perp}\) é definido de\[r_{\perp} = r \, \sin \, \theta \nonumber\] forma que\[\tau = r_{\perp}F. \nonumber\]
O braço perpendicular da alavanca\(r_{\perp}\) é a menor distância do ponto de articulação até a linha ao longo da qual\(F\) atua. A unidade SI para torque é newton-metro (N\ cdot m). A segunda condição necessária para alcançar o equilíbrio é que o torque externo líquido em um sistema deve ser zero:\[ net \, \tau = 0 \nonumber\] por convenção, os torques no sentido anti-horário são positivos e os torques no sentido horário são negativos.

Glossário

torque: eficácia de giro ou torção de uma força

braço de alavanca perpendicular: a menor distância do ponto de articulação até a linha ao longo da qual se\(F\) encontra

Unidades SI de torque: newton vezes metros, geralmente escrito como N·m

centro de gravidade: o ponto em que se presume que o peso total do corpo esteja concentrado