8.7: Introdução à propulsão de foguetes

Objetivos de

Ao final desta seção, você poderá:

• Declare a terceira lei do movimento de Newton.
• Explique o princípio envolvido na propulsão de foguetes e motores a jato.
• Derive uma expressão para a aceleração do foguete.
• Discuta os fatores que afetam a aceleração do foguete.
• Descreva a função de um ônibus espacial.

Os foguetes variam em tamanho, desde fogos de artifício tão pequenos que pessoas comuns os usam para os imensos Saturn Vs que antes impulsionavam enormes cargas úteis em direção à Lua. A propulsão de todos os foguetes, motores a jato, balões vazios e até mesmo lulas e polvos é explicada pelo mesmo princípio físico — a terceira lei do movimento de Newton. A matéria é ejetada à força de um sistema, produzindo uma reação igual e oposta sobre o que resta. Outro exemplo comum é o recuo de uma arma. A arma exerce uma força sobre uma bala para acelerá-la e, consequentemente, experimenta uma força igual e oposta, causando o recuo ou chute da arma.

Fazendo conexões: experimento para levar para casa — Propulsão de um balão

• Segure um balão e encha-o com ar. Então, solte o balão. Em que direção o ar sai do balão e em que direção o balão é impulsionado? Se você encher o balão com água e depois soltá-lo, a direção do balão muda? Explique sua resposta.

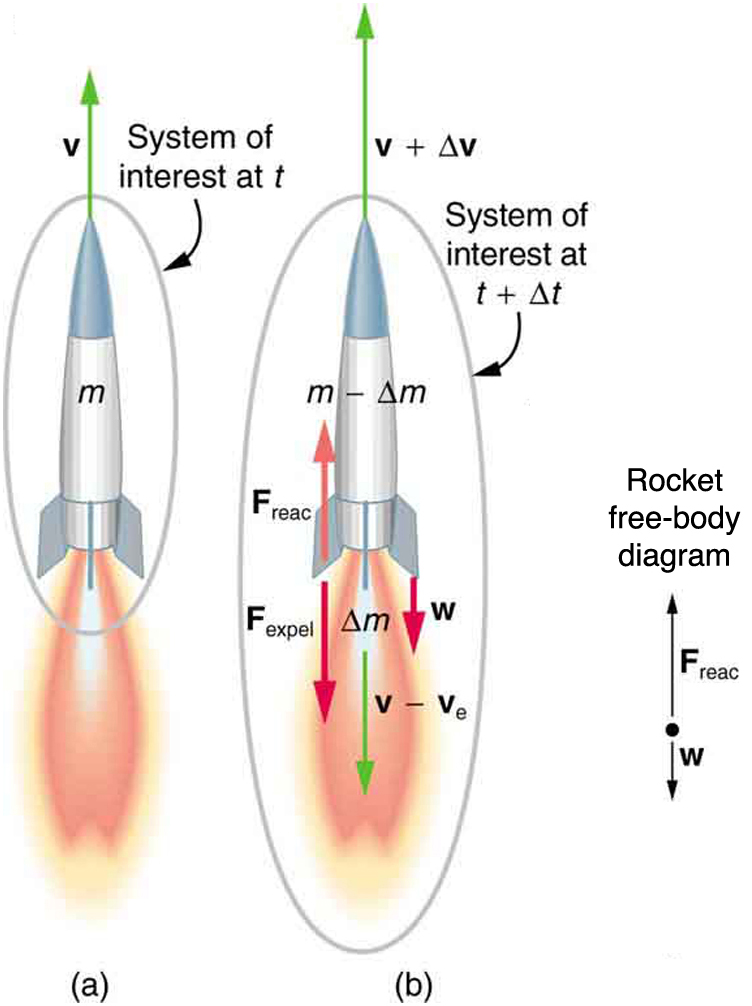
A figura\(\PageIndex{1}\) mostra um foguete acelerando em linha reta. Na parte (a), o foguete tem uma massa\(m\) e uma velocidade em\(v\) relação à Terra e, portanto, um momento\(mv\) Na parte (b),\(\Delta t\) passou um tempo em que o foguete ejetou uma massa\(\Delta m\) de gás quente a uma velocidade em\(v_e\) relação ao foguete. O restante da massa\((m - \Delta m)\) agora tem uma velocidade maior\((v + \Delta v)\). O momentum de todo o sistema (foguete mais gás expelido) realmente diminuiu porque a força da gravidade atuou por um tempo\(\Delta t\), produzindo um impulso negativo\(\Delta p = -mg\Delta t\). (Lembre-se de que o impulso é a força externa líquida em um sistema multiplicada pelo tempo em que ele age e é igual à mudança no momentum do sistema.) Portanto, o centro de massa do sistema está em queda livre, mas, ao expulsar rapidamente a massa, parte do sistema pode acelerar para cima. É um equívoco comum pensar que o escapamento do foguete é empurrado para o solo. Se considerarmos o empuxo, ou seja, a força exercida sobre o foguete pelos gases de escape, então o empuxo de um foguete é maior no espaço sideral do que na atmosfera ou na plataforma de lançamento. Na verdade, os gases são mais fáceis de expelir para o vácuo. Ao calcular a mudança no momento de todo o sistema e igualar essa mudança ao impulso, a seguinte expressão pode ser mostrada como uma boa aproximação para a aceleração do foguete.\(\Delta t\)

\[a = \dfrac{v_e}{m} \dfrac{\Delta m}{\Delta t} - g,\]

onde\(a\) está a aceleração do foguete,\(v_e\) é a velocidade de escape,\(m\) é a massa do foguete,\(\ Delta m\) é a massa do gás ejetado e\(\Delta t\) é o tempo em que o gás é ejetado.

Figura\(\PageIndex{1}\): (a) Este foguete tem uma massa\(m\) e uma velocidade ascendente\(v\). A força externa líquida no sistema é\(-mg\), se a resistência do ar for negligenciada. (b) Um tempo\(\Delta t\) depois, o sistema tem duas partes principais, o gás ejetado e o restante do foguete. A força de reação no foguete é o que supera a força gravitacional e a acelera para cima.

A aceleração de um foguete depende de três fatores principais, consistentes com a equação de aceleração de um foguete. Primeiro, quanto maior a velocidade de exaustão dos gases em relação ao foguete\(v_e\), maior será a aceleração. O limite prático para\(v_e\) é aproximadamente\(2.5 \times 10^3 \, m/s\) para sistemas de propulsão a gás quente convencionais (não nucleares). O segundo fator é a taxa na qual a massa é ejetada do foguete. Esse é o fator\((\Delta m/\Delta t)v_e\), com unidades de newtons, chamado de “empuxo”. Quanto mais rápido o foguete queima seu combustível, maior seu empuxo e maior sua aceleração. O terceiro fator é a massa\(m\) do foguete. Quanto menor for a massa (todos os outros fatores são iguais), maior será a aceleração. A massa do foguete\(m\) diminui drasticamente durante o voo porque a maior parte do foguete é combustível para começar, de modo que a aceleração aumenta continuamente, atingindo um máximo pouco antes de o combustível se esgotar.

Fatores que afetam a aceleração de um foguete

• Quanto maior a velocidade de exaustão\(v_e\) dos gases em relação ao foguete, maior será a aceleração.
• Quanto mais rápido o foguete queima seu combustível, maior sua aceleração.
• Quanto menor a massa do foguete (todos os outros fatores são iguais), maior a aceleração.

Exemplo\(\PageIndex{1}\): Calculating Acceleration: Initial Acceleration of a Moon Launch

A massa de um Saturno V na decolagem era\(2.80 \times 10^6 \, kg\), sua taxa de queima de combustível era\(1.40 \times 10^4 \times kg/s\), e a velocidade de escape era\(2.40 \times 10^3 m/s\). Calcule sua aceleração inicial.

Estratégia

Esse problema é uma aplicação direta da expressão para aceleração porque é desconhecido e todos os termos do lado direito da equação são fornecidos.

Solução

Substituindo os valores fornecidos na equação pelos rendimentos de aceleração

\[\begin{align*} a &= \dfrac{v_e}{m} \dfrac{\Delta m}{\delta t} - g \\[4pt] &= \dfrac{2.40 \times 10^3 \, m/s}{2.80 \times 10^6 \, kg}(1.40 \times 10^4 \, kg/s) - 9.8 \, m/s^2 \\[4pt] &= 2.20 \, m/s^2. \end{align*}\]

Discussão

Esse valor é bastante pequeno, mesmo para uma aceleração inicial. A aceleração aumenta constantemente à medida que o foguete queima combustível, porque\(m\) diminui\(v_e\) e\(\frac{\Delta m}{\Delta t} \) permanece constante. Conhecendo essa aceleração e a massa do foguete, você pode mostrar que o empuxo dos motores foi\(3.36 \times 10^7 \, N.\)

Para atingir as altas velocidades necessárias para pular continentes, obter órbita ou escapar completamente da gravidade da Terra, a massa do foguete, exceto o combustível, deve ser a menor possível. Pode-se mostrar que, na ausência de resistência do ar e negligenciando a gravidade, a velocidade final de um foguete de um estágio inicialmente em repouso é

\[v = v_e \, ln \dfrac{m_0}{m_r},\]

onde\(ln (m_0/m_r) \) é o logaritmo natural da razão entre a massa inicial do foguete\((m_0)\) e o que resta\((m_r)\) depois que todo o combustível é esgotado. (Observe que na verdade\(v\) é a mudança na velocidade, então a equação pode ser usada para qualquer segmento do voo. Se começarmos do repouso, a mudança na velocidade é igual à velocidade final.) Por exemplo, vamos calcular a razão de massa necessária para escapar da gravidade da Terra começando do repouso, dado que a velocidade de escape da Terra é de cerca de\(11.2 \times 10^3 \, m/s\), e assumindo uma velocidade de escape\(v_e = 2.5 \times 10^3 \, m/s.\)\[ln \dfrac{m_0}{m_r} = \dfrac{v}{v_e} = \dfrac{11.2 \times 10^3 \, m/s}{2.5 \times 10^3 \, m/s} = 4.48 \] Resolvendo para\(m_0/m_r\) dá\[\dfrac{m_0}{m_r} = e^{4.48} = 88.\]

Assim, a massa do foguete é\[ m_r = \dfrac{m_0}{88}.\]

Esse resultado significa que apenas\(1/88\) uma parte da massa resta quando o combustível é queimado e\(87/88\) da massa inicial foi combustível. Expressos em porcentagens, 98,9% do foguete é combustível, enquanto a carga útil, os motores, os tanques de combustível e outros componentes representam apenas 1,10%. Levando em consideração a resistência do ar e a força gravitacional, a massa\(m_r\) restante só pode ser cerca de\(m_0/180\). É difícil construir um foguete em que o combustível tenha uma massa 180 vezes maior do que o resto. A solução são foguetes de vários estágios. Cada estágio precisa atingir apenas parte da velocidade final e é descartado após a queima do combustível. O resultado é que cada estágio sucessivo pode ter motores menores e mais carga útil em relação ao combustível. Uma vez fora da atmosfera, a relação entre carga útil e combustível também se torna mais favorável. O ônibus espacial foi uma tentativa de um veículo econômico com algumas peças reutilizáveis, como os propulsores de combustível sólido e a própria nave. (Veja a Figura) A necessidade do ônibus espacial de ser operado por humanos, no entanto, tornou o lançamento de satélites pelo menos tão caro quanto foguetes descartáveis e não tripulados. Idealmente, o ônibus espacial só teria sido usado quando atividades humanas fossem necessárias para o sucesso de uma missão, como o reparo do telescópio espacial Hubble. Foguetes com satélites também podem ser lançados de aviões. O uso de aviões tem a dupla vantagem de que a velocidade inicial está significativamente acima de zero e um foguete pode evitar a maior parte da resistência da atmosfera.

Figura: O ônibus\(\PageIndex{2}\) espacial tinha várias peças reutilizáveis. Os propulsores de combustível sólido em ambos os lados foram recuperados e reabastecidos após cada voo, e todo o orbitador retornou à Terra para uso em voos subsequentes. O grande tanque de combustível líquido estava vazio. O ônibus espacial era um conjunto complexo de tecnologias, empregando combustível sólido e líquido e revestimentos cerâmicos pioneiros como escudos térmicos de reentrada. Como resultado, permitiu vários lançamentos em oposição a foguetes de uso único. (crédito: NASA)

Explorações de Phet: Lunar Lander

Você pode evitar o campo de pedregulhos e pousar com segurança, pouco antes de o combustível acabar, como fez Neil Armstrong em 1969? Nossa versão deste videogame clássico simula com precisão o movimento real da sonda lunar com a massa, o empuxo, a taxa de consumo de combustível e a gravidade lunar corretos. A sonda lunar real é muito difícil de controlar.

Explorações de Phet: Lunar Lander

Você pode evitar o campo de pedregulhos e pousar com segurança, pouco antes de o combustível acabar, como fez Neil Armstrong em 1969? Nossa versão deste videogame clássico simula com precisão o movimento real da sonda lunar com a massa, o empuxo, a taxa de consumo de combustível e a gravidade lunar corretos. A sonda lunar real é muito difícil de controlar.

Figura\(\PageIndex{3}\): Lunar Lander

Resumo

Esta página conecta a força ao empuxo e ao peso de um foguete e raposas na segunda lei de Newton:\(a=\frac{F}{mass}.\)

• A terceira lei do movimento de Newton afirma que, para cada ação, há uma reação igual e oposta.
• A aceleração de um foguete é\(a = \frac{v_e}{m} \frac{\Delta m}{\Delta t} - g.\)
• A aceleração de um foguete depende de três fatores principais. Eles são
  1. Quanto maior a velocidade de exaustão dos gases, maior a aceleração.
  2. Quanto mais rápido o foguete queima seu combustível, maior sua aceleração.
  3. Quanto menor a massa do foguete, maior a aceleração.