Skip to main content
Global

8.5: Colisões inelásticas em uma dimensão

  1. Last updated
  2. Save as PDF
  • Page ID
    194264

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Defina colisão inelástica.
    • Explique uma colisão perfeitamente inelástica.
    • Aplique uma compreensão das colisões aos esportes.
    • Determine a velocidade de recuo e a perda de energia cinética dada a massa e a velocidade inicial.

    Vimos que em uma colisão elástica, a energia cinética interna é conservada. Uma colisão inelástica é aquela em que a energia cinética interna muda (ela não é conservada). Essa falta de conservação significa que as forças entre objetos em colisão podem remover ou adicionar energia cinética interna. O trabalho realizado por forças internas pode mudar as formas de energia dentro de um sistema. Para colisões inelásticas, como quando objetos em colisão se unem, esse trabalho interno pode transformar alguma energia cinética interna em transferência de calor. Ou pode converter energia armazenada em energia cinética interna, como quando raios explosivos separam um satélite de seu veículo de lançamento.

    Definição: Colisões inelásticas

    Uma colisão inelástica é aquela em que a energia cinética interna muda (ela não é conservada).

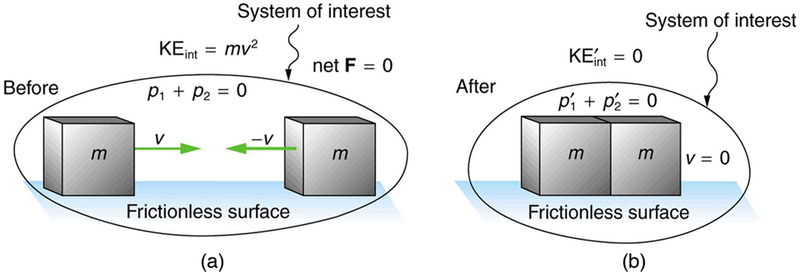
    A figura\(\PageIndex{1}\) mostra um exemplo de uma colisão inelástica. Dois objetos com massas iguais se dirigem um em direção ao outro em velocidades iguais e depois se unem. Sua energia cinética interna total é inicialmente

    \[\dfrac{1}{2}mv^2 + \dfrac{1}{2}mv^2 = mv^2.\]

    Os dois objetos descansam depois de ficarem juntos, conservando o ímpeto. Mas a energia cinética interna é zero após a colisão. Uma colisão na qual os objetos se unem às vezes é chamada de colisão perfeitamente inelástica porque reduz a energia cinética interna mais do que qualquer outro tipo de colisão inelástica. Na verdade, essa colisão reduz a energia cinética interna ao mínimo que ela pode ter, ao mesmo tempo que conserva o momento.

    O sistema de interesse contém duas massas iguais com massa m. Uma se move para a direita e a outra para a esquerda com a mesma magnitude de velocidade representada por V. Devido a isso, seu momento total e força líquida permanecem zero. A energia cinética interna é potência mv 2. Após a colisão, o sistema de interesse não tem velocidade líquida, momento total e energia cinética interna. Isso vale para todas as colisões inelásticas.
    Figura\(\PageIndex{1}\): Uma colisão unidimensional inelástica de dois objetos. O momento é conservado, mas a energia cinética interna não é conservada. (a) Dois objetos de igual massa inicialmente se dirigem diretamente um para o outro na mesma velocidade. (b) Os objetos ficam juntos (uma colisão perfeitamente inelástica) e, portanto, sua velocidade final é zero. A energia cinética interna do sistema muda em qualquer colisão inelástica e é reduzida a zero neste exemplo.

    Definição: Colisões perfeitamente inelásticas

    Uma colisão na qual os objetos se unem às vezes é chamada de “perfeitamente inelástica”.

    Exemplo\(\PageIndex{1}\): Calculating Velocity and Change in Kinetic Energy - Inelastic Collision of a Puck and a Goalie

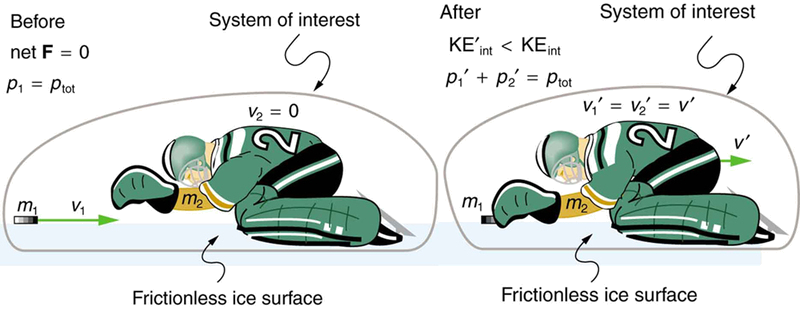
    1. Encontre a velocidade de recuo de um goleiro de hóquei no gelo de 70,0 kg, originalmente em repouso, que pega um disco de hóquei de 0,150 kg batido nele a uma velocidade de 35,0 m/s.
    2. Quanta energia cinética é perdida durante a colisão? Suponha que o atrito entre o gelo e o sistema puck-goalie seja insignificante (Figura\(\PageIndex{2}\))
    A primeira foto mostra um goleiro de hóquei no gelo de massa m 2 dobrado de joelhos, virando para a esquerda em uma superfície de gelo sem atrito com velocidade zero e um disco de hóquei de massa m 1 e velocidade V 1 movendo-se para a direita. O momento total do sistema é p 1, que é o momento do disco e a força líquida é zero. A segunda foto mostra o goleiro pegando o disco. O disco se move com a velocidade V 1prime e o goleiro com a velocidade V 2 prime e suas magnitudes são iguais. O momentum do disco é p 1 prime e o goleiro é p 2 prime. O momento total permanece o mesmo de antes da colisão. Mas a energia cinética após a colisão é menor do que a energia cinética antes da colisão. Isso vale para colisões inelásticas.
    Figura\(\PageIndex{2}\): Um goleiro de hóquei no gelo pega um disco de hóquei e recua para trás. A energia cinética inicial do disco é quase totalmente convertida em energia térmica e som nessa colisão inelástica.

    Estratégia

    O momentum é conservado porque a força externa líquida no sistema puck-goalie é zero. Assim, podemos usar a conservação do momento para encontrar a velocidade final do sistema de disco e goleiro. Note que a velocidade inicial do goleiro é zero e que a velocidade final do disco e do goleiro é a mesma. Uma vez encontrada a velocidade final, as energias cinéticas podem ser calculadas antes e depois da colisão e comparadas conforme solicitado.

    Solução para (a)

    O momentum é conservado porque a força externa líquida no sistema puck-goalie é zero.

    A conservação do momentum é

    \[p_1 + p_2 = p'_1 + p'_2 \nonumber\]

    ou

    \[m_1v_1 + m_2v_2 = m_1v'_1 + m_2v'_2. \nonumber\]

    Como o goleiro está inicialmente em repouso, sabemos que\(v_2 = 0.\) porque o goleiro pega o disco, as velocidades finais são iguais, ou\(v'_1 = v'_2 = v'.\) assim, a equação de conservação do momento simplifica para

    \[m_1v_1 = (m_1 + m_2)v'. \nonumber\]

    Solução para obter\(v'\) rendimentos

    \[v' = \dfrac{m_1}{m_1 + m_2}v_1. \nonumber\]

    Inserindo valores conhecidos nesta equação, obtemos

    \[\begin{align*} v' &= \left( \dfrac{0.150 \, kg}{70.0 \, kg + 0.150 \, kg} \right)(35.0 \, m/s) \\[5pt] &= 7.48 \times 10^{-2} m/s)^2 \\[5pt] &= 0.196 \, J. \end{align*}\]

    A mudança na energia cinética interna é, portanto,

    \[\begin{align*} KE'_{int} - KE_{int} &= 0.196 \, J - 91.9 \, J \\[5pt] &= -91.7 \, J \end{align*}\]

    onde o sinal de menos indica que a energia foi perdida.

    Discussão para (b)

    Quase toda a energia cinética interna inicial é perdida nessa colisão perfeitamente inelástica. \(KE_{int} \)é convertido principalmente em energia térmica e som.

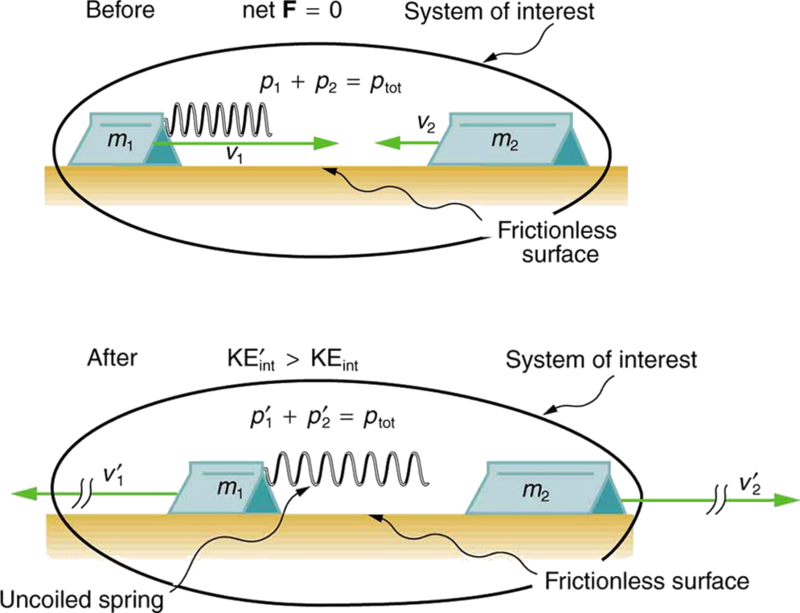
    Durante algumas colisões, os objetos não se unem e menos energia cinética interna é removida, como acontece na maioria dos acidentes automobilísticos. Alternativamente, a energia armazenada pode ser convertida em energia cinética interna durante uma colisão. \(\PageIndex{3}\)A figura mostra um exemplo unidimensional em que dois carrinhos em uma pista de ar colidem, liberando energia potencial de uma mola comprimida. O exemplo\(\PageIndex{2}\) trata dos dados dessa colisão.

    Uma mola desenrolada é conectada a um planador com área de seção transversal triangular de massa m 1 que se move com a velocidade v 1 para a direita. Outro planador sólido de massa m 2 e área de seção transversal triangular se move para a esquerda com velocidade V 2 em uma superfície sem atrito. O momento total é a soma de seu momento individual p 1 e p 2. Após a colisão, m 1 se move para a esquerda com velocidade V 1 prime e momento p 1prime. M 2 se move para a direita com a velocidade V 2 prime. Seu momentum individual se torna p 1prime e p 2 prime, mas o momentum total permanece o mesmo. A energia cinética interna após a colisão é maior do que a energia cinética antes da colisão.
    Figura\(\PageIndex{3}\): Uma pista aérea é quase sem atrito, de modo que o impulso é conservado. O movimento é unidimensional. Nesta colisão, examinada em Exemplo\(\PageIndex{2}\), a energia potencial de uma mola comprimida é liberada durante a colisão e convertida em energia cinética interna.

    As colisões são particularmente importantes nos esportes e a indústria esportiva e de lazer utiliza colisões elásticas e inelásticas. Vejamos brevemente o tênis. Lembre-se de que, em uma colisão, é o momento e não a força que importa. Portanto, uma raquete de tênis mais pesada terá a vantagem sobre uma mais leve. Essa conclusão também vale para outros esportes: um bastão leve (como um taco de softball) não consegue acertar uma bola dura muito longe.

    A localização do impacto da bola de tênis na raquete também é importante, assim como a parte do golpe durante a qual o impacto ocorre. Um movimento suave resulta na maximização da velocidade da bola após o impacto e reduz lesões esportivas, como o cotovelo de tenista. Um jogador de tênis tenta acertar a bola no “ponto ideal” da raquete, onde a vibração e o impacto são minimizados e a bola pode receber mais velocidade. A ciência e as tecnologias do esporte também usam conceitos de física, como movimento e movimento rotacional e vibrações.

    Experiência para levar para casa: pular uma bola de tênis

    1. Encontre uma raquete (uma raquete de tênis, badminton ou outra raquete serve). Coloque a raquete no chão e fique na alça. Solte uma bola de tênis nas cordas a partir de uma altura medida. Meça a altura em que a bola salta. Agora peça a um amigo que segure a raquete com firmeza pela alça e solte uma bola de tênis da mesma altura medida acima da raquete. Meça a altura em que a bola salta e observe o que acontece com a mão do seu amigo durante a colisão. Explique suas observações e medidas.
    2. O coeficiente de restituição\((c)\) é uma medida da elasticidade de uma colisão entre uma bola e um objeto e é definido como a razão das velocidades antes e antes da colisão. Uma colisão perfeitamente elástica tem um\(c\) de 1. Para uma bola quicando no chão (ou uma raquete no chão),\(c\) pode ser mostrado\(c = (h/H)^{1/2} \) onde\(h\) está a altura em que a bola salta e\(H\) é a altura da qual a bola cai. Determine\(c\) os casos da Parte 1 e o caso de uma bola de tênis quicando em um piso de concreto ou madeira (\(c = 0.85 \)para novas bolas de tênis usadas em uma quadra de tênis).

    Exemplo\(\PageIndex{2}\): Calculating Final Velocity and Energy Release - Two Carts Collide

    Na colisão mostrada na Figura\(\PageIndex{3}\), dois carros colidem inelasticamente. O carrinho 1 (indicado)\(m_1\) carrega uma mola que é inicialmente comprimida. Durante a colisão, a mola libera sua energia potencial e a converte em energia cinética interna. A massa do carrinho 1 e da mola é de 0,350 kg, e a carreta e a mola juntas têm uma velocidade inicial de\(-0.500 \, m/s\). Após a colisão, observa-se que o carrinho 1 recua com uma velocidade de\(-4.00 \, m/s\).

    1. Qual é a velocidade final do carrinho 2?
    2. Quanta energia foi liberada pela mola (supondo que toda ela tenha sido convertida em energia cinética interna)?

    Estratégia

    Podemos usar a conservação do momento para encontrar a velocidade final do carrinho 2, porque\(F_{net} = 0\) (a pista não tem atrito e a força da mola é interna). Uma vez determinada essa velocidade, podemos comparar a energia cinética interna antes e depois da colisão para ver quanta energia foi liberada pela mola.

    Solução para (a)

    Como antes, a equação para conservação do momento em um sistema de dois objetos é

    \[m_1v_1 + m_2v_2 = m_1v'_1 + m_2v'_2. \nonumber\]

    A única incógnita nessa equação é\(v'_2.\) Resolver\(v'_2\) e substituir valores conhecidos nos campos de equação anteriores.

    \[\begin{align*} v'_2 &= \dfrac{m_1v_1 + m_2v_2 - m_1v'_1}{m_2} \\[5pt] &= \dfrac{0.350 \, kg)(2.00 \, m/s) + (0.500 \, kg)(-0.500 \, m/s)}{0.500 \, kg} - \dfrac{(0.350 \, kg)(-4.00 \, m/s)}{0.500 \, kg} \\[5pt] &= 3.70 \, m/s.\end{align*}\]

    Solução para (b)

    A energia cinética interna antes da colisão é

    \[\begin{align*} KE_{int} &= \dfrac{1}{2}m_1v_1^2 + \dfrac{1}{2} m_2v_2^2 \\[5pt] &= \dfrac{1}{2}(0.350 \, kg)(2.00 \, m/s)^2 + \dfrac{1}{2}(0.500 \, kg)(-0.500 \, m/s)^2 \\[5pt] &= 0.763 \, J. \end{align*}\]

    Após a colisão, a energia cinética interna é

    \[\begin{align*} KE'_{int} &= \dfrac{1}{2}m_1v_1^{'2} + \dfrac{1}{2} m_2v_2^{'2} \\[5pt] &= \dfrac{1}{2}(0.350 \, kg)(-4.00 \, m/s)^2 + \dfrac{1}{2}(0.500 \, kg)(0.370 \, m/s)^2 \\[5pt] &= 6.22 \, J. \end{align*}\]

    A mudança na energia cinética interna é, portanto,

    \[\begin{align*} KE' - KE &= 6.22 \, J - 0.763 \, J \\[5pt] &= 5.46 \, J. \end{align*}\]

    Discussão

    A velocidade final do carrinho 2 é grande e positiva, o que significa que ele está se movendo para a direita após a colisão. A energia cinética interna nessa colisão aumenta em 5,46 J. Essa energia foi liberada pela mola.

    Resumo

    • Uma colisão inelástica é aquela em que a energia cinética interna muda (ela não é conservada).
    • Uma colisão na qual os objetos se unem às vezes é chamada de perfeitamente inelástica porque reduz a energia cinética interna mais do que qualquer outro tipo de colisão inelástica.
    • A ciência e as tecnologias do esporte também usam conceitos de física, como movimento e movimento rotacional e vibrações.

    Glossário

    colisão inelástica
    uma colisão na qual a energia cinética interna não é conservada
    colisão perfeitamente inelástica
    uma colisão na qual os objetos em colisão se unem