Skip to main content
Global

8.4: Colisões elásticas em uma dimensão

  1. Last updated
  2. Save as PDF
  • Page ID
    194265

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Descreva uma colisão elástica de dois objetos em uma dimensão.
    • Defina a energia cinética interna.
    • Derive uma expressão para conservação da energia cinética interna em uma colisão unidimensional.
    • Determine as velocidades finais em uma colisão elástica dadas as massas e as velocidades iniciais.

    Vamos considerar vários tipos de colisões de dois objetos. Essas colisões são as mais fáceis de analisar e ilustram muitos dos princípios físicos envolvidos nas colisões. O princípio de conservação do momento é muito útil aqui e pode ser usado sempre que a força externa líquida em um sistema for zero.

    Começamos com a colisão elástica de dois objetos se movendo ao longo da mesma linha — um problema unidimensional. Uma colisão elástica é aquela que também conserva a energia cinética interna. A energia cinética interna é a soma das energias cinéticas dos objetos no sistema. A figura ilustra uma colisão elástica na qual a energia cinética interna e o momento são conservados.

    Colisões verdadeiramente elásticas só podem ser alcançadas com partículas subatômicas, como elétrons atingindo núcleos. As colisões macroscópicas podem ser quase, mas não totalmente elásticas — alguma energia cinética é sempre convertida em outras formas de energia, como a transferência de calor devido ao atrito e ao som. Uma colisão macroscópica que é quase elástica é a de dois blocos de aço no gelo. Outra colisão quase elástica é aquela entre dois carros com amortecedores de mola em uma pista de ar. Superfícies geladas e trilhos de ar são quase sem atrito, permitindo mais facilmente colisões quase elásticas sobre elas.

    Colisão elástica

    Uma colisão elástica é aquela que conserva a energia cinética interna.

    Energia cinética interna

    A energia cinética interna é a soma das energias cinéticas dos objetos no sistema.

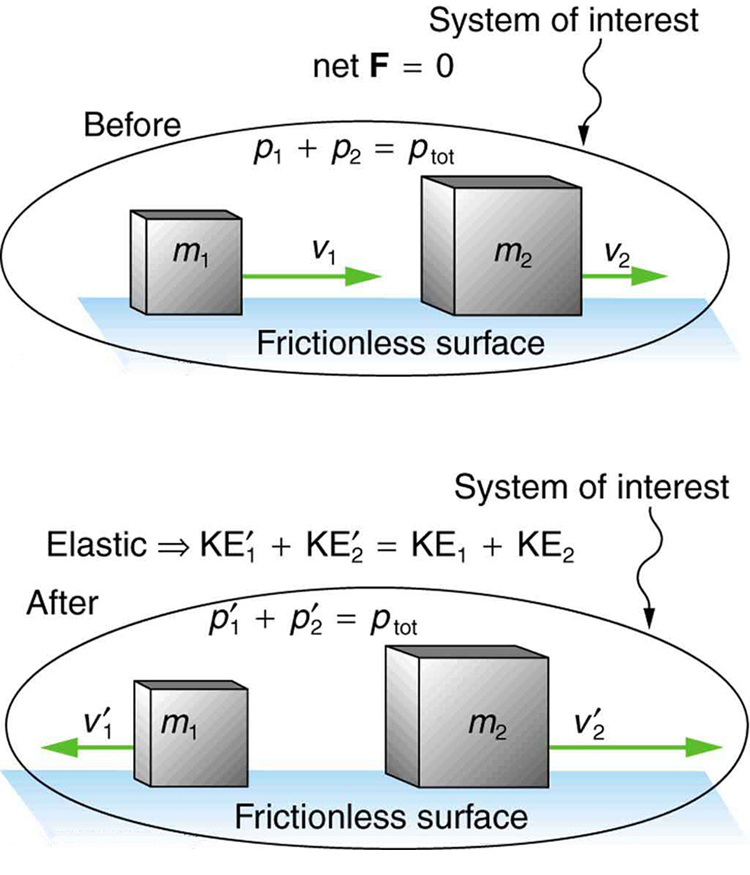
    O sistema de interesse contém uma massa menor m sub1 e uma massa maior m sub2 movendo-se em uma superfície sem atrito. M sub 2 se move com velocidade V sub 2 e momento p sub 2 e m sub 1 se move atrás de m sub 2, com velocidade V sub 1 e impulso p sub 1 na direção certa. P 1 mais P 2 é igual a p total. A força líquida é zero. Após a colisão, m sub 1 se move para a esquerda com a velocidade V sub 1, enquanto m sub 2 se move para a direita com a velocidade V sub 2 na mesma superfície sem atrito. O momento de m sub 1 se torna p 1 prime e m 2 se torna p 2 prime agora. P 1 primo mais p 2 primo é igual a p total.
    Figura\(\PageIndex{1}\): Uma colisão elástica unidimensional de dois objetos. O momento e a energia cinética interna são conservados.

    Agora, para resolver problemas envolvendo colisões elásticas unidimensionais entre dois objetos, podemos usar as equações para conservação do momento e conservação da energia cinética interna. Primeiro, a equação para conservação do momento para dois objetos em uma colisão unidimensional é

    \[p_1 +p_2 = p'_1 + p'_2 \, (F_{net} = 0)\]ou

    \[m_1v_1 + m_2 v_2 = m_1 v'_1 + m'_2v'_2 \, (F_{net} = 0),\]

    onde os números primos (') indicam valores após a colisão. Por definição, uma colisão elástica conserva energia cinética interna e, portanto, a soma das energias cinéticas antes da colisão é igual à soma após a colisão. Assim,

    \[ \dfrac{1}{2} m_1 v_1^2 + \dfrac{1}{2} m_2 v_2^2 = \dfrac{1}{2} m_1 v_1^{'2} + \dfrac{1}{2} m_2 v_2^{'2} \]

    expressa a equação para conservação da energia cinética interna em uma colisão unidimensional.

    Exemplo\(\PageIndex{1}\): Calculating Velocities Following an Elastic Collision

    Calcule as velocidades de dois objetos após uma colisão elástica, considerando que

    \[m_1 = 0.500 \, kg, \, m_2 = 3.50 \, kg, \, v_1 = 4.00 \, m/s, \, and \, v_2 = 0,\]

    Estratégia e conceito

    Primeiro, visualize o que significam as condições iniciais: um objeto pequeno atinge um objeto maior que está inicialmente em repouso. Essa situação é um pouco mais simples do que a situação mostrada na Figura em que os dois objetos estão se movendo inicialmente. Somos convidados a encontrar duas incógnitas (as velocidades finais\(v'_1\) e\( v'_2\)). Para encontrar duas incógnitas, devemos usar duas equações independentes. Como essa colisão é elástica, podemos usar as duas equações acima. Ambos podem ser simplificados pelo fato de que o objeto 2 está inicialmente em repouso e, portanto,\(v_2 = 0.\) uma vez simplificadas essas equações, as combinamos algebricamente para resolver as incógnitas.

    Solução

    Para esse problema, observe isso\(v_2 = 0\) e use a conservação do momentum. Assim,

    \[p_1 = p'_1 + p'_2\]ou

    \[m_1v_1 = m_1v'_1 + m_2v'_2.\]

    Usando a conservação da energia cinética interna e isso\(v_2 = 0\),

    \[\dfrac{1}{2}m_1v_1^2 = \dfrac{1}{2}mv_1v_1^{'2} + \dfrac{1}{2}mv_2v_2^{'2}.\]

    Resolvendo a primeira equação (equação de momento) para\(v'_2\), obtemos

    \[v'_2 = \dfrac{m_1}{m_2}(v_1 - v'_1).\]

    Substituir essa expressão na segunda equação (equação interna da energia cinética) elimina a variável\(v'_2\), deixando apenas\(v'_1\) como uma incógnita (a álgebra é deixada como um exercício para o leitor). Existem duas soluções para qualquer equação quadrática; neste exemplo, elas são desconhecidas (a álgebra é deixada como um exercício para o leitor). Existem duas soluções para qualquer equação quadrática; neste exemplo, elas são

    \[v'_1 = 4.00 \, m/s\]e

    \[v'_1 = -3.00 \, m/s.\]

    Conforme observado quando equações quadráticas foram encontradas em capítulos anteriores, ambas as soluções podem ou não ser significativas. Nesse caso, a primeira solução é a mesma que a condição inicial. A primeira solução, portanto, representa a situação antes da colisão e é descartada. A segunda solução\((v'_1 = -3.00 \, m/s\)) é negativa, o que significa que o primeiro objeto salta para trás. Quando esse valor negativo de\(v'_1\) é usado para encontrar a velocidade do segundo objeto após a colisão, obtemos

    \[v'_2 = \dfrac{m_1}{m_2}(v_1 - v'_1) = \dfrac{0.500 \, kg}{3.50 \, kg}[4.00 - (-3.00)] \, m/s\]ou

    \[v'_2 = 1.00 \, m/s.\]

    Discussão

    O resultado desse exemplo é intuitivamente razoável. Um objeto pequeno atinge um objeto maior em repouso e salta para trás. O maior é empurrado para frente, mas com baixa velocidade. (É como um carro compacto pulando para trás em um SUV de tamanho normal que está inicialmente em repouso.) Para verificar, tente calcular a energia cinética interna antes e depois da colisão. Você verá que a energia cinética interna permanece inalterada em 4,00 J. Verifique também o momento total antes e depois da colisão; você descobrirá que ele também está inalterado.

    As equações para conservação do momento e da energia cinética interna, conforme descritas acima, podem ser usadas para descrever qualquer colisão elástica unidimensional de dois objetos. Essas equações podem ser estendidas para mais objetos, se necessário. '4. 100 m/s

    Fazendo conexões: investigação para levar para casa — Ice Cubes and Elastic

    Colisão

    Encontre alguns cubos de gelo que tenham aproximadamente o mesmo tamanho e uma mesa de cozinha lisa ou uma mesa com tampo de vidro. Coloque os cubos de gelo na superfície a vários centímetros um do outro. Mova um cubo de gelo em direção a um cubo de gelo estacionário e observe o caminho e as velocidades dos cubos de gelo após a colisão. Tente evitar colisões de ponta e colisões com cubos de gelo giratórios. Você criou colisões aproximadamente elásticas? Explique as velocidades e direções dos cubos de gelo usando o momentum.

    EXPLORAÇÕES PHET: LABORATÓRIO DE COLISÕES

    Investigue colisões em uma mesa de air hockey. Configure seus próprios experimentos: varie o número de discos, massas e condições iniciais. O momentum é conservado? A energia cinética é conservada? Varie a elasticidade e veja o que acontece.

    PhET_Icon.png
    Figura\(\PageIndex{2}\): Laboratório de colisão

    Resumo

    • Uma colisão elástica é aquela que conserva a energia cinética interna.
    • A conservação da energia cinética e do momento juntos permite que as velocidades finais sejam calculadas em termos de velocidades e massas iniciais em colisões unidimensionais de dois corpos.
     

    Glossário

    colisão elástica
    uma colisão que também conserva energia cinética interna
    energia cinética interna
    a soma das energias cinéticas dos objetos em um sistema