6.2: Aceleração centrípeta

Last updated
Save as PDF

Page ID: 194634

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Estabeleça a expressão para aceleração centrípeta.
Explique a centrífuga.

Sabemos pela cinemática que a aceleração é uma mudança na velocidade, seja em sua magnitude ou em sua direção, ou ambas. No movimento circular uniforme, a direção da velocidade muda constantemente, então sempre há uma aceleração associada, mesmo que a magnitude da velocidade possa ser constante. Você mesmo experimenta essa aceleração quando vira uma curva em seu carro. (Se você mantiver o volante firme durante uma curva e se mover em velocidade constante, estará em um movimento circular uniforme.) O que você percebe é uma aceleração lateral porque você e o carro estão mudando de direção. Quanto mais nítida a curva e maior sua velocidade, mais perceptível essa aceleração se tornará. Nesta seção, examinamos a direção e a magnitude dessa aceleração.

A figura\(\PageIndex{1}\) mostra um objeto se movendo em um caminho circular em velocidade constante. A direção da velocidade instantânea é mostrada em dois pontos ao longo do caminho. A aceleração está na direção da mudança na velocidade, que aponta diretamente para o centro de rotação (o centro do caminho circular). Esse apontamento é mostrado com o diagrama vetorial na figura. Chamamos a aceleração de um objeto que se move em movimento circular uniforme (resultante de uma força externa líquida) de aceleração centrípeta\(a_c\); centrípeta significa “em direção ao centro” ou “busca ao centro”.

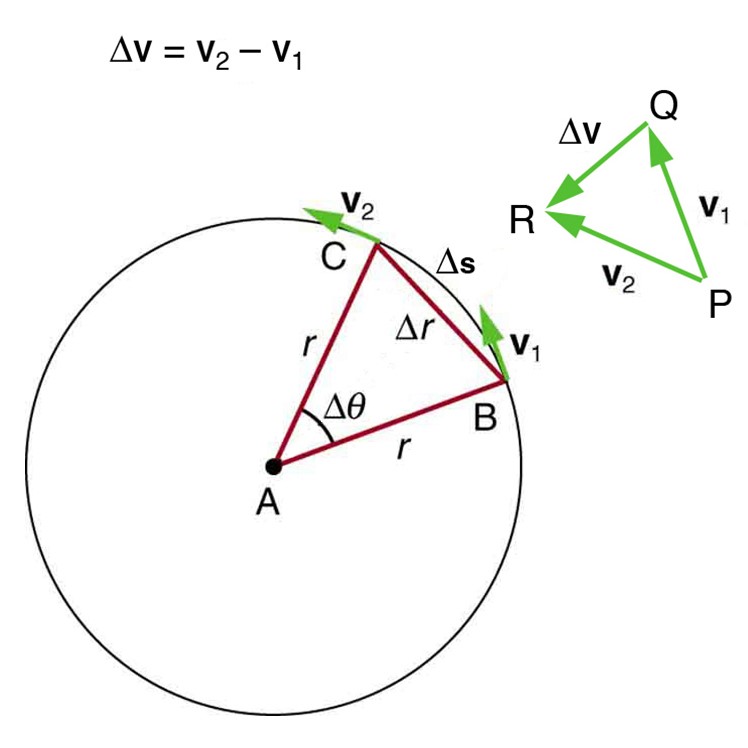
A figura dada mostra um círculo, com um triângulo com vértices A B C feitos do centro até o limite. A está no centro e os pontos B e C estão no caminho do círculo. As linhas A B e A C atuam como raios e B C é um acorde. Delta teta é mostrado dentro do triângulo, e o comprimento do arco delta s e o comprimento da corda delta r também são fornecidos. No ponto B, a velocidade do objeto é mostrada como v um e no ponto C, a velocidade do objeto é mostrada como v dois. Ao longo do círculo, uma equação é mostrada como delta v igual a v sub 2 menos v sub 1. — Figura: As\(\PageIndex{1}\) direções da velocidade de um objeto em dois pontos diferentes são mostradas, e a mudança na velocidade é\(\Delta v\) vista apontando diretamente para o centro da curvatura. (Veja uma pequena inserção.) Porque\(a_c = \Delta v/ \Delta t, \) a aceleração também está voltada para o centro;\(a_c\) é chamada de aceleração centrípeta. (Como\(\delta \theta \) é muito pequeno, o comprimento do arco\( \Delta s\) é igual ao comprimento do acorde\(\Delta r \) para pequenas diferenças de tempo.)

A direção da aceleração centrípeta é em direção ao centro da curvatura, mas qual é sua magnitude? Observe que o triângulo formado pelos vetores de velocidade e o formado pelos raios\(r\)\(\Delta s\) são semelhantes. Ambos os triângulos ABC e PQR são triângulos isósceles (dois lados iguais). Os dois lados iguais do triângulo vetorial de velocidade são as velocidades.\( v_1 =v_2 = v \) Usando as propriedades de dois triângulos semelhantes, obtemos

\[ \dfrac{\Delta v}{v} = \dfrac{\Delta s}{r}. \]

A aceleração é\(\Delta v/\Delta t \) e, portanto, primeiro resolvemos essa expressão para\(\delta v \):

\[\delta v = \dfrac{v}{r} \Delta s. \]

Em seguida, dividimos isso por\(\Delta t \), produzindo

\[\dfrac{\Delta v}{\Delta t} = \dfrac{v}{r} \times \dfrac{\Delta s}{\Delta t}. \]

Finalmente, observando que\( \Delta v/\Delta t = a_c \) e que\(\delta s/\Delta t = v \) a velocidade linear ou tangencial, vemos que a magnitude da aceleração centrípeta é

\[ a_c = \dfrac{v^2}{r}, \]

que é a aceleração de um objeto em um círculo de raio\(r\) em uma velocidade\(v\).

Portanto, a aceleração centrípeta é maior em altas velocidades e em curvas nítidas (raio menor), como você notou ao dirigir um carro. Mas é um pouco surpreendente que\(a_c\) seja proporcional à velocidade ao quadrado, o que implica, por exemplo, que é quatro vezes mais difícil fazer uma curva a 100 km/h do que a 50 km/h. Uma curva afiada tem um raio pequeno, então isso\(a_c\) é maior para curvas mais apertadas, como você provavelmente notou.Também é útil para expresso\(a_c\) em termos de velocidade angular. \( v = r\omega \)Substituindo a expressão acima, encontramos\( a_c = (r \omega^2)/r = r \omega^2 \). Podemos expressar a magnitude da aceleração centrípeta usando uma das duas equações:

\[ a_c = \dfrac{v^2}{r}; \, a_c = r \omega^2 \]

Lembre-se de que a direção de\(a_c\) é em direção ao centro. Você pode usar qualquer expressão mais conveniente, conforme ilustrado nos exemplos abaixo.

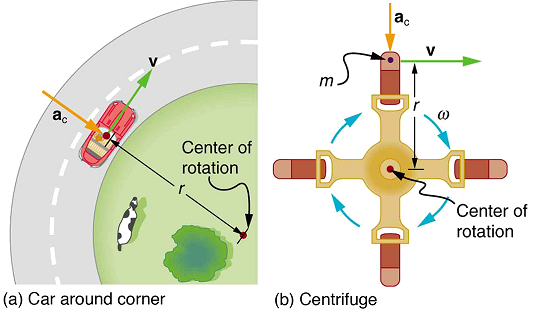
Uma centrífuga (Figura\(\PageIndex{2b}\)) é um dispositivo rotativo usado para separar amostras de diferentes densidades. A alta aceleração centrípeta diminui significativamente o tempo necessário para que a separação ocorra e possibilita a separação com amostras pequenas. As centrífugas são usadas em uma variedade de aplicações na ciência e na medicina, incluindo a separação de suspensões unicelulares, como bactérias, vírus e células sanguíneas, de um meio líquido e a separação de macromoléculas, como DNA e proteína, de uma solução. As centrífugas são frequentemente classificadas em termos de sua aceleração centrípeta em relação à aceleração devido à gravidade. A aceleração centrípeta\((g)\) máxima de várias centenas de milhares\(g\) é possível no vácuo. Centrífugas humanas, centrífugas extremamente grandes, têm sido usadas para testar a tolerância dos astronautas aos efeitos de acelerações maiores que a da gravidade da Terra.

Exemplo \(\PageIndex{1}\): Centripetal Acceleration vs. Gravity?

Qual é a magnitude da aceleração centrípeta de um carro seguindo uma curva de raio de 500 m a uma velocidade de 25,0 m/s (cerca de 90 km/h)? Compare a aceleração com a devida à gravidade para essa curva bastante suave obtida na velocidade da rodovia. Veja a Figura\(\PageIndex{2a}\).

Estratégia

Como\(v\) e\(r\) são dadas, a primeira expressão em\( a_c = \frac{v^2}{r}: \, a_c = r \omega^2 \) é a mais conveniente de usar.

Solução

Inserindo os valores fornecidos de\( v = 25.0 \, m/s and r = 500 \, m \) na primeira expressão para\(a_c\) dá

\[a_c = \dfrac{v^2}{r} = \dfrac{(25.0 m/s)^2}{500 \, m} = 1.25 \, m/s^2. \nonumber \]

Discussão

Para comparar isso com a aceleração devido à gravidade\( (g = 9.80 \, m/s^2) \), tomamos a proporção de\(a_c/g = (1.25 \, m/s^2)/(9.80 \, m/s^2) = 0.128. \) Assim,\(a_c = 0.128 g \) e é perceptível, especialmente se você não estiver usando cinto de segurança.

Na figura a, um carro mostrado de cima está rodando em uma estrada circular em torno de um caminho circular. O centro do parque é denominado como o centro desse círculo e a distância desse ponto até o carro é tomada como raio r. A velocidade linear é mostrada na direção perpendicular em direção à frente do carro, mostrada como v a aceleração centrípeta é mostrada com uma seta apontada para o centro de rotação . Na figura b, uma centrífuga é mostrada e um objeto de massa m está girando nela a uma velocidade constante. O objeto está a uma distância igual ao raio, r, da centrífuga. A aceleração centrípeta é mostrada em direção ao centro de rotação, e a velocidade, v, é mostrada perpendicularmente ao objeto no sentido horário. — Figura\(\PageIndex{2}\): (a) O carro que segue um caminho circular em velocidade constante é acelerado perpendicularmente à sua velocidade, conforme mostrado. A magnitude dessa aceleração centrípeta é encontrada no Exemplo. (b) Uma partícula de massa em uma centrífuga está girando a uma velocidade angular constante. Ele deve ser acelerado perpendicularmente à sua velocidade ou continuaria em linha reta. A magnitude da aceleração necessária é encontrada no Exemplo.

Exemplo \(\PageIndex{2}\): Qual é o tamanho da aceleração centrípeta em uma ultracentrífuga?

Calcule a aceleração centrípeta de um ponto 7,50 cm do eixo de uma ultracentrífuga girando em\(7.4 \times 10^7 \, rev/min.\) Determine a razão dessa aceleração com a devida à gravidade. Veja a Figura\(\PageIndex{2b}\).

Estratégia

O termo rev/min significa revoluções por minuto. Ao converter isso em radianos por segundo, obtemos a velocidade angular\(\omega\). Como\(r\) é dado, podemos usar a segunda expressão na equação\(a_c = \frac{v^2}{r}; \, a_c = r\omega^2 \) para calcular a aceleração centrípeta.

Solução

\(7.40 \times 10^4 \, rev/min \)Para converter em radianos por segundo, usamos o fato de que uma revolução é\(2\pi \, rad\) e um minuto é 60,0 s. Assim,

\[\omega = 7.40 \times 10^4 \dfrac{rev}{min} \times \dfrac{2 \pi \, rad}{1 \, rev} \times \dfrac{1 \, min}{60 \, sec} = 7745 \, rad/sec. \nonumber \]

Agora, a aceleração centrípeta é dada pela segunda expressão em\( a_c = \frac{v^2}{r}; \, a_c = r\omega^2\) como

\[ a_c = r\omega^2. \nonumber\]

A conversão de 7,50 cm em metros e a substituição de valores conhecidos fornece

\[a_c = (0.0750 \, m)(7854 \, rad/sec)^2 = 4.50 \times 10^6 \, m/s^2. \nonumber\]

Observe que os radianos sem unidades são descartados para obter as unidades corretas para aceleração centrípeta. Tomando a proporção de\(a_c\) para\(g\) rendimentos

\[\dfrac{a_c}{g} = \dfrac{4.63 \times 10^6}{9.80} = 4.59 \times 10^5. \nonumber\]

Discussão

Esse último resultado significa que a aceleração centrípeta é 472.000 vezes mais forte que\(g\). Não é de admirar que essas\(\omega\) centrifugadoras altas sejam chamadas de ultracentrífugas. As acelerações extremamente grandes envolvidas diminuem muito o tempo necessário para causar a sedimentação das células sanguíneas ou de outros materiais.

É claro que uma força externa líquida é necessária para causar qualquer aceleração, assim como Newton propôs em sua segunda lei do movimento. Portanto, uma força externa líquida é necessária para causar uma aceleração centrípeta. Na seção sobre Força Centrípeta, consideraremos as forças envolvidas no movimento circular.

EXPLORAÇÕES DE PHET: LADYBUG MOTION 2D

Saiba mais sobre vetores de posição, velocidade e aceleração. Mova a joaninha definindo a posição, velocidade ou aceleração e veja como os vetores mudam. Escolha movimento linear, circular ou elíptico e grave e reproduza o movimento para analisar o comportamento.

Resumo

A aceleração centrípeta\(a_c\) é a aceleração experimentada em movimento circular uniforme. Ele sempre aponta para o centro de rotação. É perpendicular à velocidade linear\(v\) e tem a magnitude\[a_c = \dfrac{v^2}{r}; \, a_c = r\omega^2. \nonumber \]
A unidade de aceleração centrípeta é\(m/s^2.\)

Glossário

aceleração centrípeta: a aceleração de um objeto se movendo em um círculo, direcionado para o centro

ultracentrifugadora: uma centrífuga otimizada para girar um rotor em velocidades muito altas