Skip to main content
Global

6.1: Ângulo de rotação e velocidade angular

  1. Last updated
  2. Save as PDF
  • Page ID
    194659

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Defina o comprimento do arco, o ângulo de rotação, o raio de curvatura e a velocidade angular.
    • Calcule a velocidade angular da rotação da roda de um carro.

    Em Cinemática, estudamos o movimento ao longo de uma linha reta e introduzimos conceitos como deslocamento, velocidade e aceleração. A cinemática bidimensional lidou com o movimento em duas dimensões. O movimento de projéteis é um caso especial de cinemática bidimensional em que o objeto é projetado no ar, enquanto está sujeito à força gravitacional, e pousa a uma distância. Neste capítulo, consideramos situações em que o objeto não pousa, mas se move em uma curva. Começamos o estudo do movimento circular uniforme definindo duas quantidades angulares necessárias para descrever o movimento rotacional.

    Ângulo de rotação

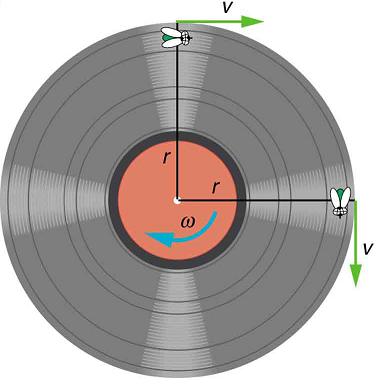
    Quando os objetos giram em torno de algum eixo — por exemplo, quando o CD (CD) na Figura gira em torno de seu centro — cada ponto do objeto segue um arco circular. Considere uma linha do centro do CD até a borda. Cada fosso usado para gravar som ao longo dessa linha se move pelo mesmo ângulo na mesma quantidade de tempo. O ângulo de rotação é a quantidade de rotação e é análogo à distância linear. Definimos o ângulo de rotação\(\Delta \theta\) como sendo a razão entre o comprimento do arco e o raio de curvatura:

    \[\Delta \theta = \dfrac{\Delta s}{r}. \]

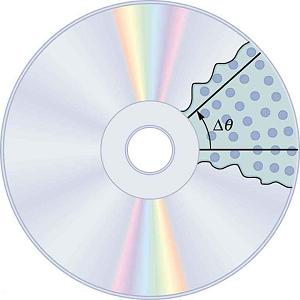
    A figura mostra a parte traseira de um disco compacto. Há uma parte riscada no lado superior direito do C D, com cerca de um quinto do tamanho de toda a área, com pontos circulares internos claramente visíveis. Dois segmentos de linha são desenhados envolvendo a área riscada da borda do C D até a parte plástica central. Uma seta curva é desenhada entre os dois segmentos de linha próximos a essa parte central e o ângulo delta teta escrito ao lado dela.
    Figura\(\PageIndex{1}\): Todos os pontos em um CD viajam em arcos circulares. Os poços ao longo de uma linha do centro até a borda se movem pelo mesmo ângulo\(\Delta \theta\) em um tempo\(\Delta t\).
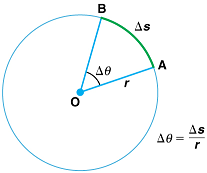
    Um círculo de raio r e centro O é mostrado. Um raio O-A do círculo é girado através do ângulo delta teta em torno do centro O para terminar como raio O-B. O comprimento do arco A-B está marcado como delta s.
    Figura\(\PageIndex{2}\): O raio de um círculo é girado em um ângulo\(\Delta \theta \). O comprimento do arco\(\delta s\) é descrito na circunferência.

    O comprimento do arco\(\Delta s\) é a distância percorrida ao longo de um caminho circular, conforme mostrado na Figura. Observe que é o raio de curvatura do caminho circular. Sabemos que, para uma revolução completa, o comprimento do arco é a circunferência de um círculo de raio\(r\). A circunferência de um círculo é\(2 \pi r\).

    Assim, para uma revolução completa, o ângulo de rotação é\[\Delta \theta = \dfrac{2\pi r}{r} = 2\pi. \]

    Esse resultado é a base para definir as unidades usadas para medir os ângulos de rotação,\(\Delta \theta \) como radianos (rad), definidas de forma que

    \[2 \pi \, radians = 1 \space revolution. \]

    Uma comparação de alguns ângulos úteis expressos em graus e radianos é mostrada na Tabela\(\PageIndex{1}\).

    Tabela\(\PageIndex{1}\): Comparação em unidades angulares
    Medida de grau Medida radiana
    \(30^o\) \(\dfrac{\pi}{6}\)
    \(60^o\) \(\dfrac{\pi}{3}\)
    \(90^o\) \(\dfrac{\pi}{2}\)
    \(120^o\) \(\dfrac{2\pi}{3}\)
    \(135^o\) \(\dfrac{3\pi}{4}\)
    \(180^o\) \(\pi\)
    Um círculo é mostrado. Dois raios do círculo, inclinados em um ângulo agudo delta teta, são mostrados. Em um dos raios, dois pontos, um e dois estão marcados. O ponto um está dentro do círculo através do qual um arco entre os dois raios é mostrado. O ponto dois está na circunferência do círculo. Os dois comprimentos de arco são delta s um e delta s dois, respectivamente, para os dois pontos.
    Figura\(\PageIndex{3}\): Os pontos 1 e 2 giram no mesmo ângulo\((\Delta \theta)\), mas o ponto 2 se move por um comprimento de arco maior\((\Delta s)\) porque está a uma distância maior do centro de rotação\((r)\).

    Se\(\Delta \theta = 2 \pi \, rad \) sim, então o CD fez uma revolução completa e cada ponto do CD está de volta à sua posição original. Como há\(360^o\) em um círculo ou uma revolução, a relação entre radianos e graus é, portanto,

    \[ 2\pi \, rad = 360^o \]

    para que

    \[ 1 \, rad = \dfrac{360^o}{2\pi} \approx 57.3^o \]

    Velocidade angular

    Com que rapidez um objeto gira? Definimos velocidade angular\(\omega\) como a taxa de mudança de um ângulo. Em símbolos, isso é

    \[\omega = \dfrac{\Delta \theta}{\Delta t}, \]

    onde uma rotação angular\(\Delta \theta \) ocorre em um tempo\(\Delta t\). Quanto maior o ângulo de rotação em um determinado período de tempo, maior a velocidade angular. As unidades de velocidade angular são radianos por segundo (rad/s). A velocidade angular\(\omega\) é análoga à velocidade linear\(v\). Para obter a relação precisa entre a velocidade angular e linear, novamente consideramos um fosso no CD rotativo. Esse fosso move um comprimento de arco\(\Delta s\) em um tempo e\(\Delta t\), portanto, tem uma velocidade linear

    \[v = \dfrac{\Delta s}{\Delta t}.\]

    A partir de\(\Delta \theta = \frac{\Delta s}{r} \) nós vemos isso\(\Delta s = r\Delta \theta \). Substituindo isso na expressão “\(v\)dá”

    \[v = \dfrac{r \Delta \theta}{\Delta t} = r\omega. \]

    Escrevemos esse relacionamento de duas maneiras diferentes e obtemos dois insights diferentes:

    \[ v = r \omega, \, or \, \omega = \dfrac{v}{r}.\]

    A primeira relação em\( v = r \omega, \, or \, \omega = \dfrac{v}{r}\) afirma que a velocidade linear\(v\) é proporcional à distância do centro de rotação, portanto, é maior para um ponto na borda (maior\(r\)), como você poderia esperar. Também podemos chamar essa velocidade linear\(v\) de um ponto na borda de velocidade tangencial. A segunda relação em\(v = r \omega, \, or \, \omega = \dfrac{v}{r}\) pode ser ilustrada considerando o pneu de um carro em movimento. Observe que a velocidade de um ponto na borda do pneu é igual à velocidade\(v\) do carro. Veja a Figura Então, quanto mais rápido o carro se move, quanto mais rápido o pneu gira - grande\(v\) significa um grande\(\omega\), porque\(v = r\omega\). Da mesma forma, um pneu de raio maior girando na mesma velocidade angular\((\omega)\) produzirá uma velocidade linear maior\((v)\) para o carro.

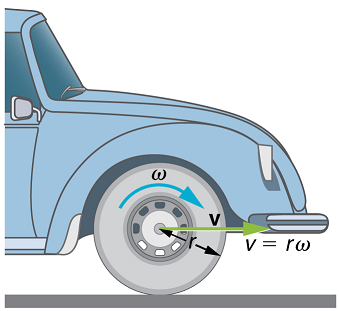
    A figura dada mostra a roda dianteira de um carro. O raio da roda do carro, r, é mostrado como uma seta e a velocidade linear, v, é mostrada com uma seta horizontal verde apontando para a direita. A velocidade angular, ômega, é mostrada com uma seta curva no sentido horário sobre a roda.
    Figura\(\PageIndex{4}\): Um carro se movendo a uma velocidade\(v\) para a direita tem um pneu girando com uma velocidade angular\(\omega\). A velocidade da banda de rodagem do pneu em relação ao eixo é\(v\) a mesma que se o carro estivesse levantado. Assim, o carro avança em velocidade linear\(v = r\omega\), onde\(r\) está o raio do pneu. Uma velocidade angular maior para o pneu significa uma velocidade maior para o carro.

    Exemplo\(\PageIndex{1}\): How Fast Does the Car Tire Spin?

    Calcule a velocidade angular de um pneu de carro com raio de 0,300 m quando o carro viaja a\(15.0 m/s\) (aproximadamente\(54 \, km/h\)). Veja a Figura.

    Estratégia

    Como a velocidade linear do aro do pneu é a mesma do carro, nós temos\(v = 15.0 m/s\). O raio do pneu é determinado como sendo\(r = 0.300 \, m\). Sabendo\(v\) e\(r\), podemos usar a segunda relação em\(v = \omega r\),\(\omega = \frac{v}{r}\) para calcular a velocidade angular.

    Solução

    Para calcular a velocidade angular, usaremos a seguinte relação:

    \[\omega = \dfrac{v}{r}.\]

    Substituindo os conhecidos,

    \[\omega = \dfrac{15.0 \, m/s}{0.300 \, m} = 50.0 \, rad/s.\]

    Discussão

    Quando cancelamos unidades no cálculo acima, obtemos 50,0/s. Mas a velocidade angular deve ter unidades de rad/s. Como os radianos são, na verdade, sem unidades (radianos são definidos como uma razão de distância), podemos simplesmente inseri-los na resposta para a velocidade angular. Observe também que se um terrestre com pneus muito maiores, digamos 1,20 m de raio, estivesse se movendo na mesma velocidade de 15,0 m/s, seus pneus girariam mais lentamente. Eles teriam uma velocidade angular

    \[ \omega = (15.0 \, m/s)/(1.20 \, m) = 12.5 \, rad/s.\]

    Ambos\(\omega\)\(v\) têm direções (portanto, são velocidades angulares e lineares, respectivamente). A velocidade angular tem apenas duas direções em relação ao eixo de rotação — no sentido horário ou anti-horário. A velocidade linear é tangente ao caminho, conforme ilustrado na Figura.

    EXPERIÊNCIA PARA LEVAR PARA CASA

    Amarre um objeto na ponta de uma corda e gire-o em um círculo horizontal acima da cabeça (gire no pulso). Mantenha a velocidade uniforme à medida que o objeto gira e meça a velocidade angular do movimento. Qual é a velocidade aproximada do objeto? Identifique um ponto próximo à sua mão e faça as medidas apropriadas para calcular a velocidade linear nesse ponto. Identifique outros movimentos circulares e meça suas velocidades angulares.

    A figura apresentada mostra a vista superior de um disco de vinil à moda antiga. Dois segmentos de linha perpendicular são desenhados através do centro do registro circular, um verticalmente para cima e outro horizontal para o lado direito. Duas moscas são mostradas nos pontos finais das linhas verticais próximas às bordas do registro. Duas setas também são desenhadas perpendicularmente para a direita através dos pontos finais dessas linhas verticais, representando velocidades lineares. Uma seta curva também é desenhada na parte circular central do registro, que mostra a velocidade angular.
    Figura\(\PageIndex{5}\): Quando um objeto se move em um círculo, aqui uma mosca na borda de um disco de vinil antiquado, sua velocidade instantânea é sempre tangente ao círculo. A direção da velocidade angular é no sentido horário neste caso.

    EXPLORAÇÕES DE PHET: A REVOLUÇÃO DA JOANINHA

    Junte-se à joaninha em uma exploração do movimento rotacional. Gire o carrossel para alterar seu ângulo ou escolha uma velocidade angular constante ou aceleração angular. Explore como o movimento circular se relaciona com a posição x, y, velocidade e aceleração do bug usando vetores ou gráficos.

    Resumo da seção

    • O movimento circular uniforme é o movimento em um círculo em velocidade constante. O ângulo de rotação\(\delta \theta\) é definido como a razão entre o comprimento do arco e o raio de curvatura:

    \[\Delta \theta = \dfrac{\Delta s}{r} \]

    onde o comprimento do arco\(\delta s\) é a distância percorrida ao longo de um caminho circular e\(r\) é o raio de curvatura do caminho circular. A quantidade\( \Delta \theta\) é medida em unidades de radianos (rad), para as quais

    \[2\pi \, rad = 360^o = 1 \, revolution. \]

    • A conversão entre radianos e graus é\[ 1 \, rad = 57.3^o. \]
    • A velocidade angular\(\omega\) é a taxa de mudança de um ângulo,

    \[\omega = \dfrac{\Delta \theta}{\Delta t},\]

    onde uma rotação\(\Delta \theta \) ocorre em um tempo\(\Delta t\). As unidades de velocidade angular são radianos por segundo (rad/s). A velocidade linear\(v\) e a velocidade angular\(\omega\) estão relacionadas por

    \[v = r\omega, \, or \, \omega = \dfrac{v}{r}. \]

    Glossário

    comprimento do arco
    Δs, a distância percorrida por um objeto ao longo de um caminho circular
    cova
    um pequeno entalhe na trilha em espiral moldado na parte superior da camada de policarbonato do CD
    ângulo de rotação
    a razão entre o comprimento do arco e o raio de curvatura em um caminho circular:\(Δθ=\frac{Δs}{r}\)
    raio de curvatura
    raio de um caminho circular
    radianos
    uma unidade de medida de ângulo
    velocidade angular
    \(ω\), a taxa de mudança do ângulo com o qual um objeto se move em um caminho circular