5.3: Elasticidade - Estresse e tensão

Last updated
Save as PDF

Page ID: 194084

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Lei estadual de Hooke.
Explique a lei de Hooke usando representação gráfica entre deformação e força aplicada.
Discuta os três tipos de deformações, como mudanças no comprimento, cisalhamento lateral e mudanças no volume.
Descreva com exemplos o módulo de cisalhamento, o módulo de cisalhamento e o módulo de volume do jovem.
Determine a mudança no comprimento dada a massa, comprimento e raio.

Agora, passamos da consideração de forças que afetam o movimento de um objeto (como atrito e arrasto) para aquelas que afetam a forma de um objeto. Se uma escavadeira empurrar um carro contra uma parede, o carro não se moverá, mas mudará visivelmente de forma. Uma mudança na forma devido à aplicação de uma força é uma deformação. Sabe-se que até mesmo forças muito pequenas causam alguma deformação. Para pequenas deformações, duas características importantes são observadas. Primeiro, o objeto retorna à sua forma original quando a força é removida, ou seja, a deformação é elástica para pequenas deformações. Segundo, o tamanho da deformação é proporcional à força, ou seja, para pequenas deformações, a lei de Hooke é obedecida. Em forma de equação, a lei de Hooke é dada por

\[F = k \Delta L, \]

onde\(\Delta L \) é a quantidade de deformação (a mudança no comprimento, por exemplo) produzida pela força\(F\) e\(k\) é uma constante de proporcionalidade que depende da forma e composição do objeto e da direção da força. Observe que essa força é uma função da deformação;\(\Delta L\) ela não é constante como a força de atrito cinético. Reorganizando isso para

\[ \Delta L = \dfrac{F}{k} \]

deixa claro que a deformação é proporcional à força aplicada. A figura mostra a relação da lei de Hooke entre a extensão\(\Delta L\) de uma mola ou de um osso humano. Para metais ou molas, a região da linha reta à qual a lei de Hooke se aplica é muito maior. Os ossos são frágeis e a região elástica é pequena e a fratura abrupta. Eventualmente, uma tensão suficientemente grande no material fará com que ele se quebre ou se quebre. A resistência à tração é a tensão de ruptura que causará deformação permanente ou fratura de um material.

LEI DE HOOKE

\[ F = k\Delta L\]

Gráfico de linha da mudança no comprimento versus força aplicada. A linha tem uma inclinação positiva constante desde a origem na região onde a lei de Hooke é obedecida. A inclinação então diminui, com uma inclinação menor, ainda positiva, até o final da região elástica. A inclinação então aumenta dramaticamente na região de deformação permanente até a fratura ocorrer. — Figura\(\PageIndex{1}\): Um gráfico de deformação\(\Delta L\) versus força aplicada\(F\). O segmento reto é a região linear onde a lei de Hooke é obedecida. A inclinação da região reta é\(\frac{1}{k}\) Para forças maiores, o gráfico é curvo, mas a deformação ainda é elástica -\(\Delta L\) retornará a zero se a força for removida. Forças ainda maiores deformam permanentemente o objeto até que ele finalmente se frature. A forma da curva próxima à fratura depende de vários fatores, incluindo a forma como a força\(F\) é aplicada. Observe que neste gráfico a inclinação aumenta logo antes da fratura, indicando que um pequeno aumento na fratura\(F\) está produzindo um grande aumento na\(L\) proximidade da fratura.

A constante de proporcionalidade\(k\) depende de vários fatores para o material. Por exemplo, uma corda de guitarra feita de náilon se estica quando é apertada e o alongamento\(\Delta L\) é proporcional à força aplicada (pelo menos para pequenas deformações). Cordas de náilon mais grossas e de aço se esticam menos para a mesma força aplicada, o que implica que elas têm uma maior\(k\) (veja a Figura). Finalmente, todas as três cordas retornam ao seu comprimento normal quando a força é removida, desde que a deformação seja pequena. A maioria dos materiais se comportará dessa maneira se a deformação for menor que cerca de 0,1% ou cerca de 1 parte\(10^3\).

Diagrama de peso w preso a cada uma das três cordas de guitarra de comprimento inicial L zero penduradas verticalmente no teto. O peso puxa as cordas para baixo com força w. O teto puxa as cordas com força w. A primeira corda de náilon fino tem uma deformação de delta L devido à força do peso ao puxar para baixo. A corda intermediária de náilon mais grosso tem uma deformação menor. A terceira corda de aço fino tem a menor deformação. — Figura: A\(\PageIndex{2}\) mesma força, neste caso, um peso,\((w)\) aplicada a três cordas de guitarra diferentes de comprimento idêntico produz as três diferentes deformações mostradas como segmentos sombreados. A corda à esquerda é de nylon fino, a do meio é de náilon mais grosso e a da direita é de aço.

ESTIQUE-SE UM POUCO

Como você mediria a constante de proporcionalidade\(k\) de um elástico? Se um elástico se estendesse 3 cm quando uma massa de 100 g estivesse presa a ele, quanto ele se esticaria se dois elásticos semelhantes fossem presos à mesma massa, mesmo se colocados juntos em paralelo ou, alternativamente, se amarrados em série?

Agora, consideramos três tipos específicos de deformações: mudanças no comprimento (tensão e compressão), cisalhamento lateral (tensão) e mudanças no volume. Todas as deformações são consideradas pequenas, salvo indicação em contrário.

Mudanças no comprimento—tensão e compressão: módulo elástico

Uma mudança no comprimento\(\Delta L\) é produzida quando uma força é aplicada a um fio ou haste paralelo ao seu comprimento\(L_0\), esticando-o (uma tensão) ou comprimindo-o. (Veja a Figura.)

A Figura a é uma haste cilíndrica apoiada em sua extremidade com uma altura de L abaixo de zero. Dois vetores marcados com F se afastam de cada extremidade. Um contorno pontilhado indica que a haste está esticada por um comprimento de delta L. A Figura b é uma haste similar de altura L abaixo de zero, mas dois vetores rotulados como F exercem uma força em direção às extremidades da haste. Uma linha pontilhada indica que a haste está comprimida por um comprimento de delta L. — Figura\(\PageIndex{3}\) :( a) Tensão. A haste é esticada por um comprimento\(\Delta L\) quando uma força é aplicada paralelamente ao seu comprimento. (b) Compressão. A mesma haste é comprimida por forças com a mesma magnitude na direção oposta. Para deformações muito pequenas e materiais uniformes,\(\Delta L\) é aproximadamente o mesmo para a mesma magnitude de tensão ou compressão. Para deformações maiores, a área da seção transversal muda à medida que a haste é comprimida ou esticada.

Experimentos mostraram que a mudança no comprimento\((\Delta L)\) depende de apenas algumas variáveis. Como já foi dito,\(\Delta L\) é proporcional à força\(F\) e depende da substância da qual o objeto é feito. Além disso, a mudança no comprimento é proporcional ao comprimento original\(L_0\) e inversamente proporcional à área da seção transversal do fio ou haste. Por exemplo, uma corda longa de guitarra se estende mais do que uma curta, e uma corda grossa se estende menos do que uma fina. Podemos combinar todos esses fatores em uma equação para\(\Delta L\):

\[\Delta L = \dfrac{1}{Y}\dfrac{F}{A} L_0,\]

onde\(\Delta L\) está a mudança no comprimento,\(F\) a força aplicada,\(Y\) é um fator, chamado módulo de elasticidade ou módulo de Young, que depende da substância,\(A\) é a área da seção transversal e\(L_0\) é o comprimento original. A tabela lista os valores\(Y\) de vários materiais - diz-se que aqueles com uma grande\(Y\) rigidez à tração têm uma grande rigidez à tração porque se deformam menos em uma determinada tensão ou compressão.

Os módulos de Young não estão listados para líquidos e gases na Tabela porque não podem ser esticados ou comprimidos em apenas uma direção. Observe que há uma suposição de que o objeto não acelera, de modo que na verdade existem duas forças de magnitude aplicadas\(F\) atuando em direções opostas. Por exemplo, as cordas na Figura estão sendo puxadas para baixo por uma força de magnitude\(w\) e sustentadas pelo teto, que também exerce uma força de magnitude\(w\).

Exemplo\(\PageIndex{1}\): The Stretch of a Long Cable

Os cabos de suspensão são usados para transportar gôndolas nas estações de esqui. (Veja a Figura) Considere um cabo de suspensão que inclua um vão não suportado de 3020 m. Calcule a quantidade de elasticidade no cabo de aço. Suponha que o cabo tenha um diâmetro de 5,6 cm e a tensão máxima que ele possa suportar seja\(3 \times 10^6 \, N\)

As gôndolas de esqui percorrem os cabos de suspensão. Uma vasta floresta e picos de montanhas nevadas podem ser vistos ao fundo. — Figura\(\PageIndex{4}\): As gôndolas percorrem cabos de suspensão na estação de esqui Gala Yuzawa, no Japão. (crédito: Rudy Herman, Flickr)

Estratégia

A força é igual à tensão máxima, ou\( F = 3 \times 10^6 \, N. \) A área da seção transversal é\(\pi r^2 = 2.46 \times 10^{-3} m^2.\) A equação\(\Delta l = \frac{1}{Y} \frac{F}{A} L_0 \) pode ser usada para encontrar a mudança no comprimento.

Solução

Todas as quantidades são conhecidas. Assim,

\[ \Delta L = \left( \dfrac{1}{210 \times 10^9 \, N/m^2} \right) \left( \dfrac{3.0 \times 10^6 \, N}{2.46 \times 10^{-3} \, m^2} \right ) (3020 \, m)\]\[ = 18 \, m\]

Discussão

Isso é bastante exagerado, mas apenas cerca de 0,6% do comprimento não suportado. Os efeitos da temperatura sobre o comprimento podem ser importantes nesses ambientes.

Os ossos, em geral, não se fraturam devido à tensão ou compressão. Em vez disso, eles geralmente se fraturam devido ao impacto lateral ou flexão, resultando em cisalhamento ou ruptura óssea. O comportamento dos ossos sob tensão e compressão é importante porque determina a carga que os ossos podem carregar. Os ossos são classificados como estruturas de suporte de peso, como colunas em edifícios e árvores. As estruturas de suporte de peso têm características especiais; as colunas do edifício têm hastes de reforço de aço, enquanto as árvores e os ossos são fibrosos. Os ossos em diferentes partes do corpo têm diferentes funções estruturais e são propensos a diferentes estresses. Assim, o osso na parte superior do fêmur é disposto em camadas finas separadas pela medula, enquanto em outros lugares os ossos podem ser cilíndricos e preenchidos com medula ou simplesmente sólidos. Pessoas com sobrepeso têm uma tendência a danos ósseos devido às compressões sustentadas nas articulações e tendões ósseos.

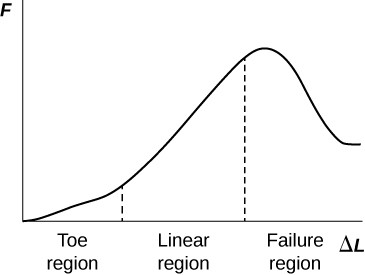
Outro exemplo biológico da lei de Hooke ocorre nos tendões. Funcionalmente, o tendão (o tecido que liga o músculo ao osso) deve se esticar facilmente no início quando uma força é aplicada, mas oferecer uma força restauradora muito maior para uma maior tensão. A figura mostra uma relação tensão-deformação para um tendão humano. Alguns tendões têm um alto teor de colágeno, então há relativamente pouca tensão ou mudança de comprimento; outros, como os tendões de apoio (como na perna), podem alterar o comprimento em até 10%. Observe que essa curva tensão-deformação não é linear, pois a inclinação da linha muda em diferentes regiões. Na primeira parte do trecho, chamada de região dos dedos, as fibras do tendão começam a se alinhar na direção do estresse — isso é chamado de descompressão. Na região linear, as fibrilas serão esticadas e, na região de falha, as fibras individuais começarão a se romper. Um modelo simples dessa relação pode ser ilustrado por molas em paralelo: molas diferentes são ativadas em diferentes comprimentos de estiramento. Exemplos disso são apresentados nos problemas no final deste capítulo. Os ligamentos (tecido que liga osso ao osso) se comportam de maneira semelhante.

A tensão no tendão dos mamíferos é mostrada por um gráfico, com tensão de tração ao longo do eixo x e tensão ao longo do eixo y. A curva tensão-deformação obtida tem três regiões, a saber, região do dedo na parte inferior, região linear entre e região de falha na parte superior. — Figura: Curva típica de\(\PageIndex{5}\) tensão-deformação para tendão de mamíferos. Três regiões são mostradas: (1) região do dedo do pé (2) região linear e (3) região de falha.

Ao contrário dos ossos e tendões, que precisam ser fortes e elásticos, as artérias e os pulmões precisam ser muito elásticos. As propriedades elásticas das artérias são essenciais para o fluxo sanguíneo. A pressão nas artérias aumenta e as paredes arteriais se esticam quando o sangue é bombeado para fora do coração. Quando a válvula aórtica se fecha, a pressão nas artérias diminui e as paredes arteriais relaxam para manter o fluxo sanguíneo. Quando você sente seu pulso, está sentindo exatamente isso: o comportamento elástico das artérias à medida que o sangue jorra a cada bomba do coração. Se as artérias fossem rígidas, você não sentiria um pulso. O coração também é um órgão com propriedades elásticas especiais. Os pulmões se expandem com esforço muscular quando inspiramos, mas relaxamos livremente e elasticamente quando expiramos. Nossas peles são particularmente elásticas, especialmente para os jovens. Um jovem pode ir de 100 kg a 60 kg sem flacidez visível na pele. A elasticidade de todos os órgãos diminui com a idade. O envelhecimento fisiológico gradual por meio da redução da elasticidade começa no início dos anos 20.

Exemplo \(\PageIndex{1}\): Calculating Deformation: How Much Does Your Leg Shorten

Quando você se posiciona nela?

Calcule a mudança no comprimento do osso da parte superior da perna (o fêmur) quando um homem de 70,0 kg suporta 62,0 kg de sua massa nele, assumindo que o osso seja equivalente a uma haste uniforme de 40,0 cm de comprimento e 2,00 cm de raio.

Estratégia

A força é igual ao peso suportado, ou\[ F = mg = (62.0 \, kg)(9.80 \, m/s^2) = 607.6 \, N, \] e a área da seção transversal é\(\pi r^2 = 1.257 \times 10^{-3} m^2. \) A equação\(\Delta L = \frac{1}{Y} \frac{F}{A} L_0 \) pode ser usada para encontrar a mudança no comprimento.

Solução

Todas as quantidades, exceto\(\Delta L\) as conhecidas. Observe que o valor de compressão do módulo de Young para osso deve ser usado aqui. Assim,

\[\Delta L = \left( \dfrac{1}{9 \times 10^9 \, N/m^2} \right) \left(\dfrac{607.6 \, N}{1.257 \times 10^{-3}} \right) (0.400 \, m) \]

\[ = 2 \times 10^{-5} \, m \]

Discussão

Essa pequena mudança no comprimento parece razoável, consistente com nossa experiência de que os ossos são rígidos. De fato, mesmo as forças bastante grandes encontradas durante a atividade física extenuante não comprimem ou dobram os ossos em grandes quantidades. Embora o osso seja rígido em comparação com a gordura ou o músculo, várias das substâncias listadas na Tabela têm valores maiores do módulo de Young\(Y\). Em outras palavras, eles são mais rígidos.

A equação para mudança no comprimento é tradicionalmente reorganizada e escrita da seguinte forma:

\[\dfrac{F}{A} = Y \dfrac{\Delta L}{L_0}.\]A razão entre força e área\(\frac{F}{A} \) é definida como tensão (medida em)\(N/m^2q\), e a razão entre a mudança de comprimento e comprimento\(\frac{\Delta L}{L_0} \) é definida como deformação (uma quantidade sem unidade). Em outras palavras,

\[ stress = Y \times strain. \]

Nessa forma, a equação é análoga à lei de Hooke, com tensão análoga à força e deformação análoga à deformação. Se reorganizarmos novamente essa equação na forma,\[ F = YA \dfrac{\Delta L}{L_0}, \] veremos que ela é a mesma da lei de Hooke com uma constante de proporcionalidade.\[ k = \dfrac{YA}{L_0}.\]

Essa ideia geral — de que a força e a deformação que ela causa são proporcionais para pequenas deformações — se aplica a mudanças no comprimento, flexão lateral e mudanças no volume.

ESTRESSE

A relação entre força e área\(\frac{F}{A}\) é definida como tensão medida em\(N/m^2\).

ESTIRPE

A razão entre a mudança no comprimento e no comprimento\(\frac{\Delta L}{L_0} \) é definida como deformação (uma quantidade sem unidade). Em outras palavras,

\[ stress = Y \times strain \]

Tensão lateral: módulo de cisalhamento

A figura ilustra o que se entende por tensão lateral ou força de cisalhamento. Aqui, a deformação é chamada\(\Delta x\) e é perpendicular\(L_0\), em vez de paralela, como acontece com a tensão e a compressão. A deformação por cisalhamento se comporta de forma semelhante à tensão e compressão e pode ser descrita com equações semelhantes. A expressão para deformação por cisalhamento é

\[ \Delta x = \dfrac{1}{S} \dfrac{F}{A}L_0,\]

onde\(S\) está o módulo de cisalhamento (consulte a Tabela) e\(F\) é a força aplicada perpendicularmente\(L_0\) e paralela à área da seção transversal\(A\). Novamente, para evitar que o objeto acelere, na verdade existem duas forças iguais e opostas\(F\) aplicadas em faces opostas, conforme ilustrado na Figura. A equação é lógica — por exemplo, é mais fácil dobrar um lápis longo e fino (pequeno\(A\)) do que um pequeno e grosso, e ambos são mais facilmente dobrados do que barras de aço semelhantes (grandes\(S\)).

DEFORMAÇÃO POR CISALHAMENTO

\[ \Delta x = \dfrac{1}{S} \dfrac{F}{A}L_0,\]onde\(S\) está o módulo de cisalhamento (consulte a Tabela) e\(F\) é a força aplicada perpendicularmente\(L_0\) e paralela à área da seção transversal\(A\).

Estante cortada por uma força aplicada no canto inferior direito em direção ao canto inferior esquerdo e no canto superior esquerdo em direção ao canto superior direito. — Figura\(\PageIndex{6}\): As forças de cisalhamento são aplicadas perpendicularmente ao comprimento\(L_0\) e paralelas à área\(A\), produzindo uma deformação\(\Delta x\). As forças verticais não são mostradas, mas deve-se ter em mente que, além das duas forças de cisalhamento\(F\), deve haver forças de apoio para impedir que o objeto gire. Os efeitos de distorção dessas forças de apoio são ignorados neste tratamento. O peso do objeto também não é mostrado, pois geralmente é insignificante em comparação com forças grandes o suficiente para causar deformações significativas.

O exame dos módulos de cisalhamento na Tabela revela alguns padrões reveladores. Por exemplo, os módulos de cisalhamento são menores do que os módulos de Young para a maioria dos materiais. O osso é uma exceção notável. Seu módulo de cisalhamento não é apenas maior que o módulo de Young, mas é tão grande quanto o do aço. É por isso que os ossos são tão rígidos.

A coluna vertebral (composta por 26 segmentos vertebrais separados por discos) fornece o suporte principal para a cabeça e a parte superior do corpo. A coluna vertebral tem curvatura normal para estabilidade, mas essa curvatura pode ser aumentada, levando ao aumento das forças de cisalhamento nas vértebras inferiores. Os discos suportam melhor as forças de compressão do que as forças de cisalhamento. Como a coluna não é vertical, o peso da parte superior do corpo exerce parte de ambos. Mulheres grávidas e pessoas com sobrepeso (com abdômen grande) precisam mover os ombros para trás para manter o equilíbrio, aumentando assim a curvatura da coluna e aumentando assim o componente de cisalhamento do estresse. Um ângulo aumentado devido à maior curvatura aumenta as forças de cisalhamento ao longo do plano. Essas forças de cisalhamento mais altas aumentam o risco de lesões nas costas por meio de discos rompidos. O disco lombossacral (o disco em forma de cunha abaixo da última vértebra) está particularmente em risco devido à sua localização.

Os módulos de cisalhamento para concreto e tijolo são muito pequenos; eles são muito variáveis para serem listados. O concreto usado em edifícios pode resistir à compressão, como em pilares e arcos, mas é muito pobre contra cisalhamento, como pode ser encontrado em pisos muito carregados ou durante terremotos. Estruturas modernas foram possibilitadas pelo uso de aço e concreto reforçado com aço. Quase por definição, líquidos e gases têm módulos de cisalhamento próximos de zero, porque fluem em resposta às forças de cisalhamento.

Exemplo \(\PageIndex{3}\): Calculating Force Required to Deform: That Nail Does Not

Dobre muito abaixo de uma carga.

Encontre a massa da imagem pendurada em um prego de aço, conforme mostrado na Figura, uma vez que o prego se dobra apenas\(1.80 \mu m\). (Suponha que o módulo de cisalhamento seja conhecido por duas figuras significativas.)

Diagrama mostrando a vista lateral de um prego em uma parede, deformado pelo peso de uma imagem pendurada nela. O peso w da imagem está para baixo. Há uma força igual w para cima no prego da parede. O prego tem 1 ponto e cinco zero milímetros de espessura. O comprimento do prego que está fora da parede é de cinco pontos zero zero milímetros. A deformação delta x da unha como resultado da imagem é de 1 ponto oito zero micrômetros. — Figura\(\PageIndex{7}\): Vista lateral de um prego com uma foto pendurada nele. A unha flexiona levemente (mostrada muito maior do que a real) devido ao efeito de cisalhamento do peso suportado. Também é mostrada a força ascendente da parede no prego, ilustrando que há forças iguais e opostas aplicadas nas seções transversais opostas do prego. Veja o exemplo para um cálculo da massa da imagem.

Estratégia.

A força\(F\) na unha (negligenciando o próprio peso da unha) é o peso da imagem\(w\). Se conseguirmos descobrir\(w\), então a massa da imagem é justa\(\frac{w}{g} \). A equação\(\Delta x = \frac{1}{S} \frac{F}{A}L_0 \) pode ser resolvida para\(F\).

Solução

Resolvendo a equação\(\Delta x = \frac{1}{S} \frac{F}{A}L_0 \) para\(F\), vemos que todas as outras quantidades podem ser encontradas:

\[ F = \dfrac{SA}{L_0} \Delta x. \]

\(S\)é encontrado na Tabela e é\(S = 80 \times 10^9 \, N/m^2 \). O raio\(r\) é de 0,750 mm (como visto na figura), então a área da seção transversal é

\[A = \pi r^2 = 1.77 \times 10^{-6} \, m^2. \]

O valor para também\(L_0\) é mostrado na figura. Assim,

\[ F = \dfrac{(80 \times 10^9 \, N/m^2)(1.77 \times 10^{-6} \, m^2)}{(5.00 \times 10^{-3} \, m)}(1.80 \times 10^{-6} \, m) = 51 \]

Essa força de 51 N é o peso\(w\) da imagem, então a massa da imagem é

\[ m = \dfrac{w}{g} = \dfrac{F}{g} = 5.2 \, kg. \]

Discussão

Esta é uma imagem bastante grande, e é impressionante que a unha se flexione apenas\(1.80 \mu m\) - uma quantidade indetectável a olho nu.

Mudanças no volume: Bulk Modulus

Um objeto será comprimido em todas as direções se as forças internas forem aplicadas uniformemente em todas as suas superfícies, como na Figura. É relativamente fácil comprimir gases e extremamente difícil comprimir líquidos e sólidos. Por exemplo, o ar em uma garrafa de vinho é comprimido quando é arrolhado. Mas se você tentar arrolhar uma garrafa cheia, não poderá comprimir o vinho - algumas devem ser removidas para que a rolha seja inserida. A razão para essas diferentes compressibilidades é que átomos e moléculas são separados por grandes espaços vazios nos gases, mas agrupados juntos em líquidos e sólidos. Para comprimir um gás, você deve forçar seus átomos e moléculas a se aproximarem. Para comprimir líquidos e sólidos, você deve realmente comprimir seus átomos e moléculas, e forças eletromagnéticas muito fortes neles se opõem a essa compressão.

Um cubo com área de seção transversal A e volume V zero é comprimido por uma força interna F atuando em todas as superfícies. A compressão causa uma mudança no volume delta V, que é proporcional à força por unidade de área e seu volume original. Essa mudança no volume está relacionada à compressibilidade da substância. — Figura\(\PageIndex{8}\): Uma força interna em todas as superfícies comprime esse cubo. Sua mudança de volume é proporcional à força por unidade de área e seu volume original e está relacionada à compressibilidade da substância.

Podemos descrever a compressão ou deformação de volume de um objeto com uma equação. Primeiro, notamos que uma força “aplicada uniformemente” é definida como tendo a mesma tensão, ou razão entre força e área,\(\frac{F}{A} \) em todas as superfícies. A deformação produzida é uma mudança de volume\(\Delta V,\) que se comporta de forma muito semelhante ao cisalhamento, tensão e compressão discutidos anteriormente. (Isso não é surpreendente, já que a compressão de todo o objeto equivale a compactar cada uma de suas três dimensões.) A relação da mudança no volume com outras quantidades físicas é dada por

\[ \Delta V = \dfrac{1}{B} \dfrac{F}{A} V_0, \]

onde\(B\) está o módulo de volume (consulte a Tabela),\(V_0\) é o volume original e\(\frac{F}{A} \) é a força por unidade de área aplicada uniformemente para dentro em todas as superfícies. Observe que nenhum módulo de volume é fornecido para gases.

Quais são alguns exemplos de compressão em massa de sólidos e líquidos? Um exemplo prático é a fabricação de diamantes de nível industrial por compressão de carbono com uma força extremamente grande por unidade de área. Os átomos de carbono reorganizam sua estrutura cristalina no padrão mais compacto de diamantes. Na natureza, um processo semelhante ocorre no subsolo, onde forças extremamente grandes resultam do peso do material sobrejacente. Outra fonte natural de grandes forças de compressão é a pressão criada pelo peso da água, especialmente nas partes profundas dos oceanos. A água exerce uma força interna em todas as superfícies de um objeto submerso e até mesmo na própria água. Em grandes profundidades, a água é comprimida de forma mensurável, como ilustra o exemplo a seguir.

Exemplo \(\PageIndex{4}\): Calculating Change in Volume with Deformation: How much

A água é comprimida em Great Ocean Depths?

Calcule a diminuição fracionária do volume\((\frac{\Delta V}{V_0}) \) da água do mar a 5,00 km de profundidade, onde a força por unidade de área é\(5.00 \times 10^7 \, N/m^2.\)

Estratégia

A equação\(\Delta V = \frac{1}{B} \frac{F}{A} V_0 \) é a relação física correta. Todas as quantidades na equação, exceto\(\frac{\Delta V}{V_0} \) são conhecidas.

Solução

Resolver o desconhecido\(\frac{\Delta V}{V_0} \) dá\[ \dfrac{\Delta V}{V_0} = \dfrac{1}{B} \dfrac{F}{A}. \]

Substituindo valores conhecidos pelo valor do módulo\(B\) de massa da Tabela,

\[\dfrac{\Delta V}{V_0} = \dfrac{5.00 \times 10^7 \, N/m^2}{2.2 \times 10^9 \, N/m^2} = 0.023 \]

Discussão

Embora mensurável, essa não é uma diminuição significativa no volume, considerando que a força por unidade de área é de cerca de 500 atmosferas (1 milhão de libras por pé quadrado). Líquidos e sólidos são extraordinariamente difíceis de comprimir.

Por outro lado, forças muito grandes são criadas por líquidos e sólidos quando eles tentam se expandir, mas são impedidos de fazê-lo, o que equivale a comprimi-los para um volume menor do que o normal. Isso geralmente ocorre quando um material contido se aquece, pois a maioria dos materiais se expande quando a temperatura aumenta. Se os materiais estiverem fortemente restritos, eles deformam ou quebram o recipiente. Outro exemplo muito comum ocorre quando a água congela. A água, ao contrário da maioria dos materiais, se expande quando congela e pode facilmente fraturar uma pedra, romper uma célula biológica ou quebrar um bloco do motor que fica em seu caminho.

Outros tipos de deformações, como torção ou torção, se comportam de forma análoga às deformações de tensão, cisalhamento e massa consideradas aqui.

Explorações de Phet: Masses & Springs

Um laboratório realista de massas e molas. Pendure massas nas molas e ajuste a rigidez e o amortecimento da mola. Você pode até mesmo diminuir o tempo. Transporte o laboratório para diferentes planetas. Um gráfico mostra a energia cinética, potencial e térmica de cada primavera.

Resumo

A lei de Hooke é dada por\[ F = k \Delta L\] onde\(L\) está a quantidade de deformação (a mudança no comprimento),\(F\) é a força aplicada e\(k\) é uma constante de proporcionalidade que depende da forma e composição do objeto e da direção da força. A relação entre a deformação e a força aplicada também pode ser escrita como

\[ \Delta L = \dfrac{1}{Y} \dfrac{F}{A} L_0, \]onde\(L\) está o módulo de Young, que depende da substância,\(A\) é a área da seção transversal e\(L_0\) é o comprimento original. A razão entre força e área\(\frac{F}{A} \) é definida como tensão, medida em N/m ². A razão entre a mudança no comprimento e comprimento\(\frac{\Delta L}{L_0}, \) é definida como deformação (uma quantidade sem unidade). Em outras palavras,\[ stress = Y \times strain. \]

A expressão para deformação por cisalhamento é\[ \Delta x = \dfrac{1}{S} \dfrac{F}{A} L_0, \]

onde\(S\) está o módulo de cisalhamento e\(F\) é a força aplicada perpendicularmente\(L_0\) e paralelamente à área da seção transversal\(A\).

A relação da mudança no volume com outras quantidades físicas é dada por

\[\Delta V = \dfrac{1}{B} \dfrac{F}{A} V_0,\]onde\(B\) está o módulo de volume,\(V_0\) é o volume original e\(\frac{F}{A}\) é a força por unidade de área aplicada uniformemente para dentro em todas as superfícies.

Notas de pé

Valores aproximados e médios. Os módulos de tensão e compressão\(Y\) de Young às vezes diferem, mas a média é calculada aqui. O osso tem módulos de Young significativamente diferentes para tensão e compressão.

Glossário

deformação: mudança de forma devido à aplicação de força

Lei de Hooke: relação proporcional entre a força F em um material e a deformação ΔL que ele causa, F=kΔL

resistência à tração: a tensão de ruptura que causará deformação permanente ou fração de um material

estresse: relação entre força e área

tensão: relação de mudança no comprimento em relação ao comprimento original

deformação por cisalhamento: deformação perpendicular ao comprimento original de um objeto

Material	Módulo de Young (tensão-compressão) Y\((10^9 \, N/m^2)\)	Módulo puro S\((10^9 \, N/m^2 )\)	Módulo de granel B\((10^9 \, N/m^2)\)
Alumínio	\ ((10^9\, N/m^2)\)” style="text-align:center; ">70	\ (10^9\, N/m^2)\)” style="text-align:center; ">25	\ ((10^9\, N/m^2)\)” style="text-align:center; ">75
Osso — tensão	\ ((10^9\, N/m^2)\)” style="text-align:center; ">16	\ ((10^9\, N/m^2)\)” style="text-align:center; ">80	\ (10^9\, N/m^2)\)” style="text-align:center; ">8
Osso — compressão	\ (10^9\, N/m^2)\)” style="text-align:center; ">9	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Latão	\ ((10^9\, N/m^2)\)” style="text-align:center; ">90	\ (10^9\, N/m^2)\)” style="text-align:center; ">35	\ ((10^9\, N/m^2)\)” style="text-align:center; ">75
Tijolo	\ ((10^9\, N/m^2)\)” style="text-align:center; ">15	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Concreto	\ ((10^9\, N/m^2)\)” style="text-align:center; ">20	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Vidro	\ ((10^9\, N/m^2)\)” style="text-align:center; ">70	\ ((10^9\, N/m^2)\)” style="text-align:center; ">20	\ ((10^9\, N/m^2)\)” style="text-align:center; ">30
Granito	\ ((10^9\, N/m^2)\)” style="text-align:center; ">45	\ ((10^9\, N/m^2)\)” style="text-align:center; ">20	\ ((10^9\, N/m^2)\)” style="text-align:center; ">45
Cabelo (humano)	\ ((10^9\, N/m^2)\)” style="text-align:center; ">10	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Madeira dura	\ ((10^9\, N/m^2)\)” style="text-align:center; ">15	\ ((10^9\, N/m^2)\)” style="text-align:center; ">10	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Ferro fundido	\ ((10^9\, N/m^2)\)” style="text-align:center; ">100	\ ((10^9\, N/m^2)\)” style="text-align:center; ">40	\ ((10^9\, N/m^2)\)” style="text-align:center; ">90
Liderar	\ ((10^9\, N/m^2)\)” style="text-align:center; ">16	\ (10^9\, N/m^2)\)” style="text-align:center; ">5	\ ((10^9\, N/m^2)\)” style="text-align:center; ">50
Mármore	\ ((10^9\, N/m^2)\)” style="text-align:center; ">60	\ ((10^9\, N/m^2)\)” style="text-align:center; ">20	\ ((10^9\, N/m^2)\)” style="text-align:center; ">70
Nylon	\ (10^9\, N/m^2)\)” style="text-align:center; ">5	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Poliestireno	\ ((10^9\, N/m^2)\)” style="text-align:center; ">3	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Seda	\ (10^9\, N/m^2)\)” style="text-align:center; ">6	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Fio de aranha	\ ((10^9\, N/m^2)\)” style="text-align:center; ">3	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Aço	\ ((10^9\, N/m^2)\)” style="text-align:center; ">210	\ ((10^9\, N/m^2)\)” style="text-align:center; ">80	\ ((10^9\, N/m^2)\)” style="text-align:center; ">130
Tendão	\ ((10^9\, N/m^2)\)” style="text-align:center; ">1	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">
Acetona	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">0.7
Etanol	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">0.9
Glicerina	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">4.5
Mercúrio	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ (10^9\, N/m^2)\)” style="text-align:center; ">25
Água	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">	\ ((10^9\, N/m^2)\)” style="text-align:center; ">2.2