4.5: Normal, tensão e outros exemplos de forças
- Page ID
- 194786
Objetivos de
Ao final desta seção, você poderá:
- Defina as forças normais e de tensão.
- Aplique as leis do movimento de Newton para resolver problemas envolvendo uma variedade de forças.
- Use identidades trigonométricas para resolver o peso em componentes.
Força normal
O peso (também chamado de força da gravidade) é uma força penetrante que atua em todos os momentos e deve ser neutralizada para evitar que um objeto caia. Você definitivamente percebe que deve suportar o peso de um objeto pesado empurrando-o para cima ao mantê-lo parado, conforme ilustrado na Figura (a). Mas como objetos inanimados, como uma mesa, suportam o peso de uma massa colocada sobre eles, como mostrado na Figura (b)? Quando o saco de comida para cachorro é colocado sobre a mesa, a mesa realmente cai um pouco sob a carga. Isso seria perceptível se a carga fosse colocada em uma mesa de cartas, mas mesmo objetos rígidos se deformam quando uma força é aplicada a eles. A menos que o objeto esteja deformado além de seu limite, ele exercerá uma força restauradora muito parecida com uma mola deformada (ou trampolim ou prancha de mergulho). Quanto maior a deformação, maior a força de restauração. Então, quando a carga é colocada na mesa, a mesa cede até que a força de restauração se torne tão grande quanto o peso da carga. Neste ponto, a força externa líquida sobre a carga é zero. Essa é a situação em que a carga está parada na mesa. A mesa cede rapidamente e a queda é pequena, então não percebemos isso. Mas é semelhante à flacidez de um trampolim quando você sobe nele.
Devemos concluir que tudo o que suporta uma carga, seja ela animada ou não, deve fornecer uma força ascendente igual ao peso da carga, como assumimos em alguns dos exemplos anteriores. Se a força que sustenta uma carga é perpendicular à superfície de contato entre a carga e seu suporte, essa força é definida como uma força normal e aqui é dado o símbolo\(N\). (Esta não é a unidade da força N.) A palavra normal significa perpendicular a uma superfície. A força normal pode ser menor que o peso do objeto se o objeto estiver inclinado, como você verá no próximo exemplo.
EQUÍVOCO COMUM: FORÇA NORMAL (N) VS. NEWTON (NJ)
Nesta seção, introduzimos a quantidade de força normal, que é representada pela variável\(N\) Isso não deve ser confundido com o símbolo do newton, que também é representado pela letra N. Esses símbolos são particularmente importantes para distinguir porque as unidades de uma força normal \(N\)acontece que são newtons (N). Por exemplo, a força normal\(N\) que o chão exerce sobre uma cadeira pode ser.\(N = 100 \, N\) Uma diferença importante é que a força normal é um vetor, enquanto o newton é simplesmente uma unidade. Tenha cuidado para não confundir essas letras em seus cálculos! Você encontrará mais semelhanças entre variáveis e unidades à medida que avança na física. Outro exemplo disso é a quantidade de trabalho\(W\) e a unidade de watts (W).
Exemplo\(\PageIndex{1}\): Weight on an incline, a Two-Dimensional problem
Considere o esquiador em uma inclinação mostrada na Figura. Sua massa, incluindo equipamento, é de 60,0 kg. (a) Qual é a aceleração dela se o atrito for insignificante? (b) Qual é a aceleração dela se o atrito for conhecido por ser de 45,0 N?
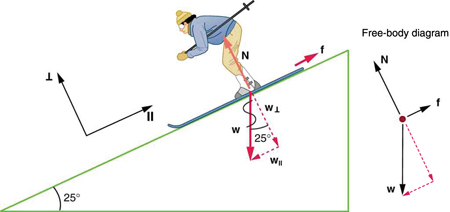
Estratégia
Esse é um problema bidimensional, já que as forças no esquiador (o sistema de interesse) não são paralelas. A abordagem que usamos na cinemática bidimensional também funciona muito bem aqui. Escolha um sistema de coordenadas conveniente e projete os vetores em seus eixos, criando dois problemas unidimensionais conectados para resolver. O sistema de coordenadas mais conveniente para o movimento em uma inclinação é aquele que tem uma coordenada paralela à inclinação e outra perpendicular à inclinação. (Lembre-se de que os movimentos ao longo de eixos perpendiculares entre si são independentes.) Usamos os símbolos\( \perp \) e\( \parallel \) para representar perpendicular e paralelo, respectivamente. Essa escolha de eixos simplifica esse tipo de problema, porque não há movimento perpendicular à inclinação e porque o atrito é sempre paralelo à superfície entre dois objetos. As únicas forças externas que atuam no sistema são o peso, o atrito e o suporte da inclinação do esquiador, respectivamente identificados\(w,\)\(f\) e\(N\) na Figura. \(N\)é sempre perpendicular à inclinação e\(f\) é paralela a ela. Mas não\(w\) está na direção de nenhum dos eixos, então o primeiro passo que damos é projetá-lo em componentes ao longo dos eixos escolhidos, definindo\(w_{\parallel}\) ser o componente de peso paralelo à inclinação e\( w_{\perp} \) o componente de peso perpendicular à inclinação. Feito isso, podemos considerar os dois problemas separados de forças paralelas à inclinação e forças perpendiculares à inclinação.
Solução
A magnitude do componente do peso paralelo à inclinação é\( w_{\parallel} = w\space sin \, (25^o)\) = mg\, sin\, (25^o),\) e a magnitude do componente do peso perpendicular à inclinação é\( w_{\perp} = w\space cos \, (25^o) = mg \, cos \, (25^o)\).
(a) Negligenciar o atrito. Como a aceleração é paralela à inclinação, precisamos considerar apenas forças paralelas à inclinação. (As forças perpendiculares à inclinação somam zero, já que não há aceleração nessa direção.) As forças paralelas à inclinação são a quantidade de peso do esquiador paralela à inclinação\(w_{\parallel} \) e ao atrito\(f\). Usando a segunda lei de Newton, com subscritos para denotar quantidades paralelas à inclinação,
\[ a_{\parallel} = \dfrac{F_{net\parallel}}{m} \]onde\(F_{net\parallel} = w_{\parallel} = mg\space sin \, (25^o) \), assumindo que não há atrito para esta peça, de modo que
\[ a_{\parallel} = \dfrac{F_{net\parallel}}{m} = \dfrac{mg\space sin(25^o)}{m} = g\space sin(25^o) \]
\[ (9.80\space m/s^2)(0.4226) = 4.14 \, m/s^2 \]
é a aceleração.
(b) Incluindo atrito. Agora temos um determinado valor de atrito e sabemos que sua direção é paralela à inclinação e se opõe ao movimento entre superfícies em contato. Portanto, a força externa líquida é agora\[ F_{net\parallel} = w_{\parallel} - f, \] e substituindo-a pela segunda lei de Newton,\(a_{\parallel} = \frac{F_{net\parallel}}{m}, \) dá
\[a_{\parallel} = \dfrac{F_{net\parallel}}{m} = \dfrac{w_{\parallel} - f}{m} = \dfrac{mg \, sin(25^o) -f}{m}. \]
Substituímos valores conhecidos para obter
\[a_{\parallel} = \dfrac{(60.0 \, kg)(9.80\space m/s^2)(0.4226) - 45.0\space N}{60.0\space kg}, \]
que rende\[a_{\parallel} = 3.39 \, m/s^2, \]
que é a aceleração paralela à inclinação quando há 45,0 N de atrito oposto.
Discussão
Como o atrito sempre se opõe ao movimento entre superfícies, a aceleração é menor quando há atrito do que quando não há nenhum. De fato, é um resultado geral que, se o atrito em uma inclinação for insignificante, a aceleração na inclinação é\(a = g\space sin\space \theta, \) independente da massa. Isso está relacionado ao fato discutido anteriormente de que todos os objetos caem com a mesma aceleração na ausência de resistência do ar. Da mesma forma, todos os objetos, independentemente da massa, deslizam para baixo em uma inclinação sem atrito com a mesma aceleração (se o ângulo for o mesmo).
RESOLVENDO PESO EM COMPONENTES
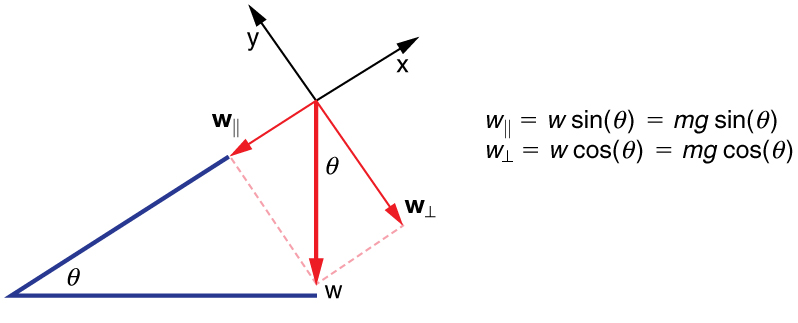
Quando um objeto repousa em uma inclinação que forma um ângulo\(\theta \) com a horizontal, a força da gravidade que atua sobre o objeto é dividida em dois componentes: uma força atuando perpendicularmente ao plano\(w_{\perp} \) e uma força atuando paralelamente ao plano,\(w_{\parallel}. \) A força perpendicular do peso, \(w_{\perp}\)é tipicamente igual em magnitude e oposto em direção à força normal,\(N\). A força atuando paralelamente ao plano\(w_{\parallel}\) faz com que o objeto acelere na inclinação. A força de atrito\(f\) se opõe ao movimento do objeto, então ele age para cima ao longo do plano.
É importante ter cuidado ao resolver o peso do objeto em componentes. Se o ângulo da inclinação estiver em um ângulo\(\theta\) com a horizontal, as magnitudes dos componentes de peso serão
\[w_{\parallel} = w\space sin\space (\theta) = mg \, sin \, (\theta) \]e
\[ w_{\perp} = w\space sin\space (\theta) = mg \, sin \, (\theta) \]
Em vez de memorizar essas equações, é útil poder determiná-las pela razão. Para fazer isso, desenhe o triângulo reto formado pelos três vetores de peso. Observe que o ângulo\(\theta\) da inclinação é o mesmo que o ângulo formado entre\(w\)\(w_{\perp} \) e. Conhecendo essa propriedade, você pode usar a trigonometria para determinar a magnitude dos componentes do peso:
\[ cos\space (\theta) = \dfrac{w_{\perp}}{w}\]
\[ w_{\perp} = w\space cos \, (\theta) = mg \, cos \, (\theta) \]
\[ sin \, (\theta) = \dfrac{w_{\parallel}}{w} \]
\[w_{\parallel} = w\space sin \, (\theta) = mg \, sin \, (\theta) \]
EXPERIÊNCIA PARA LEVAR PARA CASA: FORCE PARALELLY
Para investigar como uma força paralela a um plano inclinado muda, encontre um elástico, alguns objetos para pendurar na extremidade do elástico e uma prancha que você possa posicionar em ângulos diferentes. Quanto o elástico se estica quando você pendura o objeto na extremidade do tabuleiro? Agora coloque o tabuleiro em um ângulo para que o objeto deslize quando colocado no tabuleiro. Quanto o elástico se estende se estiver alinhado paralelamente à placa e usado para segurar o objeto parado no tabuleiro? Experimente mais dois ângulos. O que isso mostra?
Tensão
Uma tensão é uma força ao longo do comprimento de um meio, especialmente uma força transportada por um meio flexível, como uma corda ou cabo. A palavra “tensão” vem de uma palavra latina que significa “esticar”. Não por acaso, os cordões flexíveis que transportam forças musculares para outras partes do corpo são chamados de tendões. Qualquer conector flexível, como uma corda, corda, corrente, fio ou cabo, pode exercer puxões apenas paralelos ao seu comprimento; portanto, uma força transportada por um conector flexível é uma tensão com direção paralela ao conector. É importante entender que a tensão é uma tração em um conector. Em contraste, considere a frase: “Você não pode empurrar uma corda”. A força de tensão é puxada para fora ao longo das duas pontas de uma corda.
Considere uma pessoa segurando uma massa em uma corda, conforme mostrado na Figura.
A tensão na corda deve ser igual ao peso da massa suportada, como podemos provar usando a segunda lei de Newton. Se a massa de 5,00 kg na figura for estacionária, sua aceleração será zero e, portanto,\( F_{net} = 0.\) as únicas forças externas que atuam sobre a massa são seu peso\(w\) e a tensão\(T\) fornecida pelo cabo. Assim,\[ F_{net} = T - w = 0, \] onde\(T\) e\(w\) estão as magnitudes da tensão e do peso e seus sinais indicam direção, com up sendo positivo aqui. Assim, como seria de esperar, a tensão é igual ao peso da massa suportada:
\[T = w = mg. \]
Para uma massa de 5,00 kg, então (negligenciando a massa da corda) vemos que
\[ T = mg = (5.00\space kg)(9.80 \, m/s^2) = 49.0 \, N \]
Se cortarmos a corda e inserirmos uma mola, a mola estenderia um comprimento correspondente a uma força de 49,0 N, fornecendo uma observação direta e uma medida da força de tensão na corda.
Os conectores flexíveis são frequentemente usados para transmitir forças nas curvas, como em um sistema de tração hospitalar, uma articulação de dedo ou um cabo de freio de bicicleta. Se não houver atrito, a tensão é transmitida sem diminuir. Somente sua direção muda e está sempre paralela ao conector flexível. Isso é ilustrado nas Figuras (a) e (b).
Exemplo\(\PageIndex{1}\): What Is the Tension in a Tightrope?
Calcule a tensão no fio que suporta o andador de corda bamba de 70,0 kg mostrado na Figura.
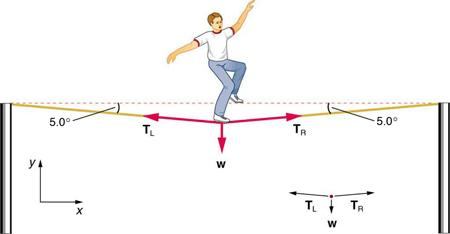
Estratégia
Como você pode ver na figura, o fio não está perfeitamente horizontal (não pode ser!) , mas está curvado sob o peso da pessoa. Assim, a tensão em ambos os lados da pessoa tem um componente ascendente que pode suportar seu peso. Como de costume, as forças são vetores representados pictorialmente por setas que têm as mesmas direções das forças e comprimentos proporcionais às suas magnitudes. O sistema é o equilibrista, e as únicas forças externas que atuam sobre ele são seu peso\(w\) e as duas tensões\(T_L\) (tensão esquerda) e\(T_R\) (tensão direita), conforme ilustrado. É razoável negligenciar o peso do próprio fio. A força externa líquida é zero, pois o sistema é estacionário. Agora, um pouco de trigonometria pode ser usada para encontrar as tensões. Uma conclusão é possível desde o início: podemos ver na parte (b) da figura que as magnitudes das tensões\(T_L\)\(T_R\) devem ser iguais. Isso ocorre porque não há aceleração horizontal na corda, e as únicas forças que atuam à esquerda e à direita são\(T_L\)\(T_R\) e. Assim, a magnitude dessas forças deve ser igual para que elas se cancelem mutuamente.
Sempre que temos problemas vetoriais bidimensionais nos quais não há dois vetores paralelos, o método mais fácil de solução é escolher um sistema de coordenadas conveniente e projetar os vetores em seus eixos. Nesse caso, o melhor sistema de coordenadas tem um eixo horizontal e outro vertical. Chamamos a horizontal de eixo\(x\) - e a vertical\(y\) de eixo y.
Solução
Primeiro, precisamos resolver os vetores de tensão em seus componentes horizontais e verticais. Isso ajuda a desenhar um novo diagrama de corpo livre mostrando todos os componentes horizontais e verticais de cada força que atua no sistema.
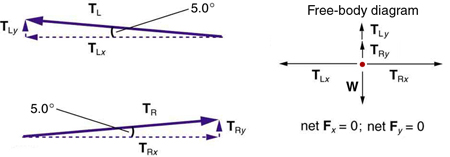
Considere os componentes horizontais das forças (indicados com um subscrito\(x\)):
\[F_{net \, x} = T_{Lx} - T_{Rx}. \]
A força horizontal externa líquida\(F_{net \, x} = 0 \), uma vez que a pessoa está parada. Assim,
\[F_{net \, x} = 0 = T_{Lx} - T_{Rx}\]
\[ T_{Lx} = T_{Rx}.\]
Agora, observe a Figura. Você pode usar a trigonometria para determinar a magnitude de\(T_L \) e\(T_R\) observe que:
\[ cos(5.0^o) = \dfrac{T_{Lx}}{T_L} \]
\[ T_{Lx} = T_L\space cos(5.0^o) \]
\[ cos(5.0^o) = \dfrac{T_{Lx}}{T_L} \]
\[T_{Rx} = T_R \, cos(5.0^o) \]
Equacionando\(T_{Lx} \) e\(T_{Rx} \):
\[ T_L \, cos(5.0^o) = T_R \, cos(5.0^o) \]
\[ T_L = T_R = T \]
como previsto. Agora, considerando os componentes verticais (indicados por um subscrito\(y\)), podemos resolver\(T\). Novamente, como a pessoa está parada, a segunda lei de Newton implica essa rede\(F_y = 0 \). Assim, conforme ilustrado no diagrama de corpo livre na Figura,
\[ F_{net \, y}= T_{Ly} + T_{Ry} - w = 0 \]
Observando a Figura, podemos usar a trigonometria para determinar a relação entre\(T_{Ly},\space T_{Ry}\)\( T \) e. Conforme determinamos a partir da análise na direção horizontal,\(T_L = T_R = T \).
\[ sin (5.0^o) = \dfrac{T_{Ly}}{T_L} \]
\[T_{Ly} = T_L \, sin (5.0^o) = T \, sin(5.0^o) \]
\[ sin (5.0^o) = \dfrac{T_{Ry}}{T_R} \]
\[ T_{Ry} = T_R \, sin(5.0^o) = T \, sin (5.0^o) \]
Agora, podemos substituir os valores por\(T_{Ly} \) e\(T_{Ry}\), na equação da força líquida na direção vertical:
\[ F_{net \, y} = T_{Ly} + T_{Ry} - w = 0 \]
\[ F_{net \, y} = T \, sin(5.0^o) + T \, sin(5.0^o) - w = 0 \]
\[ 2T \, sin(5.0^o) -w = 0 \]
\[ 2T \, sin(5.0^o) = w \]
e\[ T = \dfrac{w}{2 \, sin(5.0^o)} = \dfrac{mg}{2 \, sin(5.0^o)} \]
para que\[ T = \dfrac{(70.0 \, kg)(9.80 \, m/s^2)}{2 (0.0872)}, \]
\[ T = 3900 \, N. \]
Discussão
Observe que a tensão vertical no fio atua como uma força normal que suporta o peso do equilibrista. A tensão é quase seis vezes o peso 686-N do equilibrista. Como o fio é quase horizontal, o componente vertical de sua tensão é apenas uma pequena fração da tensão no fio. Os grandes componentes horizontais estão em direções opostas e se cancelam, portanto, a maior parte da tensão no fio não é usada para suportar o peso do equilibrista.
Se quisermos criar uma tensão muito grande, tudo o que precisamos fazer é exercer uma força perpendicular a um conector flexível, conforme ilustrado na Figura. Como vimos no último exemplo, o peso do equilibrista atuou como uma força perpendicular à corda. Vimos que a tensão na corda se relacionava com o peso do equilibrista da seguinte forma:
\[ T = \dfrac{w}{2 \, sin \, (\theta)} \]
Podemos estender essa expressão para descrever a tensão\(T\) criada quando uma força perpendicular\((F_{\perp}) \) é exercida no meio de um conector flexível:
\[ T = \dfrac{F_{\perp}}{2 \, sin \, (\theta)}. \]
Observe que\(\theta\) é o ângulo entre o conector horizontal e o dobrado. Nesse caso,\(T\) torna-se muito grande à medida que se\(\theta\) aproxima de zero. Mesmo o peso relativamente pequeno de qualquer conector flexível fará com que ele caia, pois uma tensão infinita resultaria se fosse horizontal (ou seja,\(\theta = 0 \) e\(sin \, \theta = 0 \)). (Veja a Figura.)
Tópico estendido: Forças reais e estruturas inerciais
Há outra distinção entre forças além dos tipos já mencionados. Algumas forças são reais, enquanto outras não. As forças reais são aquelas que têm alguma origem física, como a atração gravitacional. Por outro lado, forças fictícias são aquelas que surgem simplesmente porque um observador está em um quadro de referência acelerado, como aquele que gira (como um carrossel) ou sofre aceleração linear (como um carro desacelerando). Por exemplo, se um satélite estiver indo para o norte acima do hemisfério norte da Terra, então, para um observador na Terra, ele parecerá experimentar uma força a oeste que não tem origem física. Obviamente, o que está acontecendo aqui é que a Terra está girando em direção ao leste e se move para o leste sob o satélite. No quadro da Terra, isso parece uma força para o oeste no satélite, ou pode ser interpretado como uma violação da primeira lei de Newton (a lei da inércia). Um quadro de referência inercial é aquele em que todas as forças são reais e, equivalentemente, aquele em que as leis de Newton têm as formas simples dadas neste capítulo.
A rotação da Terra é lenta o suficiente para que a Terra seja quase uma estrutura inercial. Normalmente, você deve realizar experimentos precisos para observar forças fictícias e os pequenos desvios das leis de Newton, como o efeito que acabamos de descrever. Em grande escala, como na rotação dos sistemas climáticos e das correntes oceânicas, os efeitos podem ser facilmente observados.
O fator crucial para determinar se um quadro de referência é inercial é se ele acelera ou gira em relação a um quadro inercial conhecido. Salvo indicação em contrário, todos os fenômenos discutidos neste texto são considerados em quadros inerciais.
Todas as forças discutidas nesta seção são forças reais, mas há várias outras forças reais, como sustentação e empuxo, que não são discutidas nesta seção. Eles são mais especializados e não é necessário discutir todo tipo de força. É natural, no entanto, perguntar onde está a simplicidade básica que buscamos encontrar na física na longa lista de forças. Alguns são mais básicos do que outros? Existem algumas manifestações diferentes da mesma força subjacente? A resposta para ambas as perguntas é sim, como será visto na próxima seção (estendida) e no tratamento da física moderna posteriormente no texto.
EXPLORAÇÕES DE PHET: FORÇAS EM UMA DIMENSÃO
Explore as forças em ação ao tentar empurrar um armário de arquivos. Crie uma força aplicada e veja a força de atrito resultante e a força total atuando no gabinete. Os gráficos mostram as forças, a posição, a velocidade e a aceleração em relação ao tempo. Veja um diagrama de corpo livre de todas as forças (incluindo forças gravitacionais e normais).

Resumo
- Quando os objetos repousam em uma superfície, a superfície aplica uma força ao objeto que suporta o peso do objeto. Essa força de suporte atua perpendicularmente e longe da superfície. Isso é chamado de força normal,\(T\)
- Quando os objetos repousam em uma superfície horizontal não acelerada, a magnitude da força normal é igual ao peso do objeto:
\[ N = mg \]
- Quando os objetos repousam em um plano inclinado que forma um ângulo\(\theta \) com a superfície horizontal, o peso do objeto pode ser resolvido em componentes que atuam perpendicularmente\((w_{\perp})\) e paralelamente\(w_{\parallel}) \) à superfície do plano. Esses componentes podem ser calculados usando:
\[w_{\parallel} = w \, sin \, (\theta) = mg \, sin \, (\theta) \]
\[ w_{\perp} = w \, cos \, (\theta) = mg \, cos \, (\theta) \]
- A força de tração que atua ao longo de um conector flexível esticado, como uma corda ou cabo, é chamada de tensão,\ (T\.) Quando uma corda suporta o peso de um objeto que está em repouso, a tensão na corda é igual ao peso do objeto:
\[ T = mg. \]
- Em qualquer quadro de referência inercial (que não seja acelerado ou girado), as leis de Newton têm as formas simples dadas neste capítulo e todas as forças são forças reais de origem física.
Glossário
- quadro de referência inercial
- um sistema de coordenadas que não está acelerando; todas as forças que atuam em um quadro de referência inercial são forças reais, em oposição às forças fictícias que são observadas devido a um quadro de referência acelerado
- força normal
- a força que uma superfície aplica a um objeto para suportar o peso do objeto; age perpendicularmente à superfície na qual o objeto repousa
- tensão
- a força de tração que atua ao longo de um meio, especialmente um conector flexível esticado, como uma corda ou cabo; quando uma corda suporta o peso de um objeto, a força sobre o objeto devido à corda é chamada de força de tensão


