Skip to main content
Global

4.4: Terceira Lei do Movimento de Newton - Simetria nas Forças

  1. Last updated
  2. Save as PDF
  • Page ID
    194752

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Entenda a terceira lei do movimento de Newton.
    • Aplique a terceira lei de Newton para definir sistemas e resolver problemas de movimento.

    Há uma passagem no musical Man of la Mancha que se relaciona com a terceira lei do movimento de Newton. Sancho, ao descrever uma briga com sua esposa para Dom Quixote, diz: “É claro que eu bati de volta, Vossa Graça, mas ela é muito mais dura do que eu e você sabe o que dizem: 'Se a pedra bate no jarro ou o jarro bate na pedra, vai ser ruim para o jarro'”. Isso é exatamente o que acontece sempre que um corpo exerce uma força sobre outro — o primeiro também experimenta uma força (igual em magnitude e direção oposta). Inúmeras experiências comuns, como bater um dedo do pé ou jogar uma bola, confirmam isso. Está declarado com precisão na terceira lei do movimento de Newton.

    TERCEIRA LEI DO MOVIMENTO DE NEWTON

    Sempre que um corpo exerce uma força sobre um segundo corpo, o primeiro corpo experimenta uma força que é igual em magnitude e oposta em direção à força que ele exerce.

    Essa lei representa uma certa simetria na natureza: as forças sempre ocorrem em pares, e um corpo não pode exercer uma força sobre outro sem experimentar uma força em si. Às vezes nos referimos a essa lei vagamente como “ação-reação”, onde a força exercida é a ação e a força experimentada como consequência é a reação. A terceira lei de Newton tem usos práticos para analisar a origem das forças e entender quais forças são externas a um sistema.

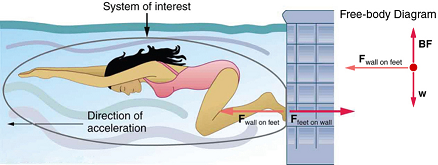
    Podemos ver facilmente a terceira lei de Newton em ação analisando como as pessoas se movimentam. Considere um nadador se afastando da lateral de uma piscina, conforme ilustrado na Figura. Ela empurra a parede da piscina com os pés e acelera na direção oposta à de seu impulso. A parede exerceu uma força igual e oposta sobre o nadador. Você pode pensar que duas forças iguais e opostas se cancelariam, mas não o fazem porque agem em sistemas diferentes. Nesse caso, existem dois sistemas que poderíamos investigar: o nadador ou a parede. Se selecionarmos o nadador para ser o sistema de interesse, como na figura, então\(F_{wall \space on \, feet} \) há uma força externa nesse sistema e afeta seu movimento. O nadador se move na direção de\(F_{wall \, on \, feet}. \) Em contraste, a força\(F_{feet \, on \, wall} \) atua na parede e não em nosso sistema de interesse. Assim, não\(F_{feet \, on \, wall} \) afeta diretamente o movimento do sistema e não cancela.\(F_{wall \, on \, feet}. \) Observe que a nadadora empurra na direção oposta à que ela deseja se mover. A reação ao impulso dela está, portanto, na direção desejada.

    Uma nadadora está exercendo uma força com os pés em uma parede dentro de uma piscina representada por uma flecha rotulada como vetor F sub Pés na parede, apontando para a direita, e a parede também está exercendo uma força igual sobre seus pés, representada por uma flecha rotulada como vetor F sub Parede sobre pés, tendo o mesmo comprimento, mas apontando para a esquerda. A direção da aceleração do nadador é para a esquerda, mostrada por uma seta para a esquerda.
    Figura\(\PageIndex{1}\): Quando a nadadora exerce uma força\(F_{feet \, on \, wall} \) na parede, ela acelera na direção oposta à do empurrão. Isso significa que a força externa líquida sobre ela está na direção oposta a\(F_{feet \, on \, wall} \) Essa oposição ocorre porque, de acordo com a terceira lei do movimento de Newton, a parede exerce uma força\(F_{wall \, on \, feet} \) sobre ela, igual em magnitude, mas na direção oposta à que ela exerce sobre ela. A linha ao redor do nadador indica o sistema de interesse. Observe que\(F_{feet \, on \, wall} \) não atua neste sistema (o nadador) e, portanto, não cancela.\(F_{wall \, on \, feet}. \) Assim, o diagrama de corpo livre mostra apenas\(F_{wall \, on \, feet}, \, w, \) a força gravitacional e\(BF,\) a força de empuxo da água que sustenta o peso do nadador. As forças verticais\(w\) e\(BF\) cancelam, pois não há movimento vertical.

    Outros exemplos da terceira lei de Newton são fáceis de encontrar. Enquanto uma professora caminha em frente a um quadro branco, ela exerce uma força para trás no chão. O piso exerce uma força de reação para frente na professora que faz com que ela acelere para frente. Da mesma forma, um carro acelera porque o solo avança nas rodas motrizes em reação às rodas motrizes empurrando para trás no chão. Você pode ver evidências de que as rodas estão empurrando para trás quando os pneus giram em uma estrada de cascalho e jogam pedras para trás. Em outro exemplo, os foguetes avançam expelindo gás para trás em alta velocidade. Isso significa que o foguete exerce uma grande força para trás sobre o gás na câmara de combustão do foguete e, portanto, o gás exerce uma grande força de reação para frente no foguete. Essa força de reação é chamada de empuxo. É um equívoco comum pensar que os foguetes se impulsionam empurrando o solo ou o ar atrás deles. Na verdade, eles funcionam melhor no vácuo, onde podem expelir mais facilmente os gases de escape. Os helicópteros também criam sustentação empurrando o ar para baixo, experimentando assim uma força de reação ascendente. Pássaros e aviões também voam exercendo força no ar em uma direção oposta à de qualquer força de que precisem. Por exemplo, as asas de um pássaro forçam o ar para baixo e para trás para se levantar e avançar. Um polvo se impulsiona na água ejetando água de seu corpo por um funil, semelhante a um jet ski. Em uma situação semelhante à de Sancho, lutadores de jaula profissionais experimentam forças de reação ao dar um soco, às vezes quebrando a mão ao atingir o corpo de um oponente.

    Exercício\(\PageIndex{1}\): Getting up to speed: Choosing the Correct System

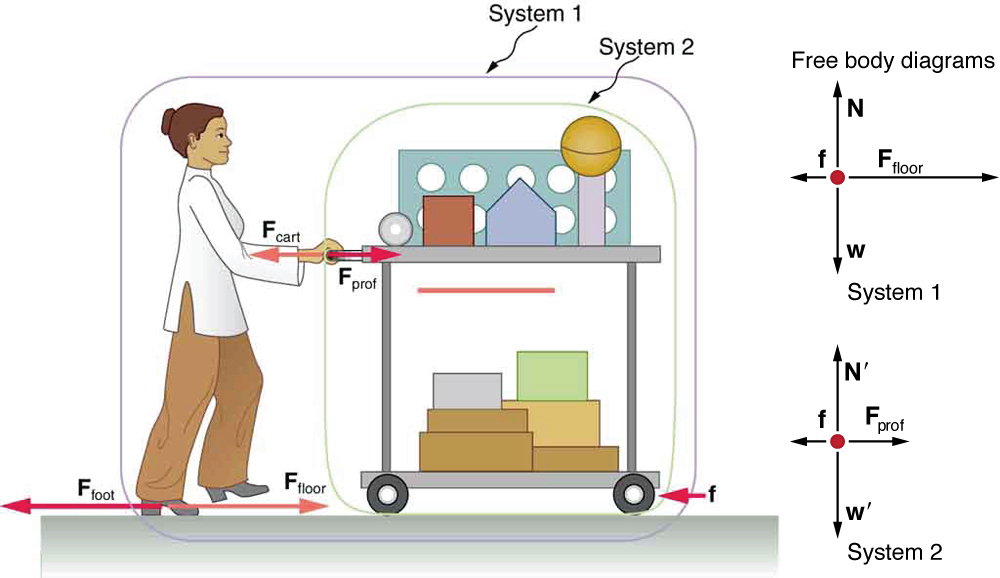
    Um professor de física empurra um carrinho de equipamento de demonstração para uma sala de aula, como pode ser visto na Figura. Sua massa é 65,0 kg, a do carrinho é 12,0 kg e a do equipamento é 7,0 kg. Calcule a aceleração produzida quando o professor exerce uma força para trás de 150 N no chão. Todas as forças que se opõem ao movimento, como atrito nas rodas do carrinho e resistência ao ar, totalizam 24,0 N.

    Um professor está empurrando um carrinho de equipamento de demonstração. Dois sistemas estão identificados na figura. O sistema um inclui o professor e o carrinho, e o sistema dois só tem o carrinho. Ela está exercendo alguma força F sub prof para a direita, mostrada por uma seta vetorial, e o carrinho também a está empurrando com a mesma magnitude de força direcionada para a esquerda, mostrada por um subcarrinho vetorial F, com o mesmo comprimento que F sub prof. A força de atrito pequena f é mostrada por uma seta vetorial apontando para a esquerda atuando entre as rodas do carrinho e o chão. A professora está empurrando o chão com os pés com uma força F subpé para a esquerda, mostrada por uma seta vetorial. O chão está empurrando seus pés com uma força que tem a mesma magnitude, F subpiso, mostrada por uma seta vetorial apontando para a direita que tem o mesmo comprimento do subpé do vetor F. Um diagrama de corpo livre também é mostrado. Para o sistema um, a força de atrito atuando para a esquerda é mostrada por uma seta vetorial com um comprimento pequeno, e a força F no subpiso está atuando para a direita, mostrada por uma seta vetorial maior que o comprimento do vetor f. No sistema dois, a força de atrito representada por um vetor curto pequeno f atua para a esquerda e outro vetor F sub prof é representado por uma seta vetorial voltada para a direita. F sub prof é maior que o pequeno f.
    Figura\(\PageIndex{2}\): Um professor empurra um carrinho de equipamento de demonstração. Os comprimentos das flechas são proporcionais às magnitudes das forças (exceto por\(f\) serem muito pequenos para serem desenhados em escala). Perguntas diferentes são feitas em cada exemplo; portanto, o sistema de interesse deve ser definido de forma diferente para cada um. O Sistema 1 é apropriado por exemplo, pois solicita a aceleração de todo o grupo de objetos. Somente\(F_{floor}\) e\(f\) são forças externas atuando no Sistema 1 ao longo da linha de movimento. Todas as outras forças cancelam ou agem no mundo exterior. O sistema 2 é escolhido para este exemplo para que\(F_{prof} \) seja uma força externa e entre na segunda lei de Newton. Observe que os diagramas de corpo livre, que nos permitem aplicar a segunda lei de Newton, variam de acordo com o sistema escolhido.

    Estratégia

    Como eles aceleram como uma unidade, definimos o sistema como professor, carrinho e equipamento. Este é o Sistema 1 na Figura. O professor empurra para trás com uma força\(F_{foot} \) de 150 N. De acordo com a terceira lei de Newton, o piso exerce uma força\(F_{floor}\) de reação para frente de 150 N no Sistema 1. Como todo movimento é horizontal, podemos supor que não há força líquida na direção vertical. O problema é, portanto, unidimensional na direção horizontal. Conforme observado,\(f\) se opõe ao movimento e, portanto, está na direção oposta de\(F_{floor}\). Observe que não incluímos as forças\(F_{prof}\) ou\(F_{cart}\) porque são forças internas, e não incluímos\(F_{foot}\) porque elas atuam no chão, não no sistema. Não há outras forças significativas atuando no Sistema 1. Se a força externa líquida puder ser encontrada em todas essas informações, podemos usar a segunda lei de Newton para encontrar a aceleração conforme solicitado. Veja o diagrama de corpo livre na figura.

    Solução

    A segunda lei de Newton é dada por\[a = \dfrac{F_{net}}{m}. \nonumber \]

    A força externa líquida no Sistema 1 é deduzida da Figura e a discussão acima é\[F_{net} = F_{floor} - f = 150 \, N - 24.0 \, N = 126 \, N. \nonumber \]

    A massa do Sistema 1 é\[m = (65.0 + 12.0 + 7.0) = 84 \, kg.\nonumber \]

    Esses valores de\(F_{net} \) e\(m\) produzem uma aceleração de\[ a = \dfrac{F_{net}}{m} \nonumber \]

    \[ a = \dfrac{126 \, N}{84 \, kg} = 1.5 \, m/s^2. \nonumber \]

    Discussão

    Nenhuma das forças entre os componentes do Sistema 1, como entre as mãos do professor e o carrinho, contribui para a força externa líquida porque elas são internas ao Sistema 1. Outra maneira de ver isso é observar que as forças entre os componentes de um sistema são canceladas porque são iguais em magnitude e opostas em direção. Por exemplo, a força exercida pelo professor na carroça resulta em uma força igual e oposta de volta sobre ela. Nesse caso, ambas as forças atuam no mesmo sistema e, portanto, cancelam. Assim, as forças internas (entre os componentes de um sistema) são canceladas. Escolher o Sistema 1 foi crucial para resolver esse problema.

    Exemplo\(\PageIndex{2}\): Force on the Cart: Choosing a New System

    Calcule a força que o professor exerce no carrinho na Figura usando dados do exemplo anterior, se necessário.

    Estratégia

    Se agora definirmos o sistema de interesse como o carrinho mais o equipamento (Sistema 2 na Figura), a força externa líquida no Sistema 2 é a força que o professor exerce na carreta menos o atrito. A força que ela exerce no carrinho\(F_{prof}\) é uma força externa atuando no Sistema 2. \(F_{prof}\)era interno ao Sistema 1, mas é externo ao Sistema 2 e entrará na segunda lei de Newton para o Sistema 2.

    Solução

    A segunda lei de Newton pode ser usada para encontrar\(F_{prof}\) Começando com\[ a = \dfrac{F_{net}}{m} \nonumber \]

    e observando que a magnitude da força externa líquida no Sistema 2 é\[ F_{net} = F_{prof} - f, \nonumber \]

    resolvemos para\(F_{prof}, \) a quantidade desejada\[ F_{net} + f.\nonumber \]

    O valor de\(f\) é dado, então devemos calcular a rede.\(F_{net}. \) Isso pode ser feito, pois tanto a aceleração quanto a massa do Sistema 2 são conhecidas. Usando a segunda lei de Newton, vemos que\[ F_{net} = ma, \nonumber \]

    onde a massa do Sistema 2 é 19,0 kg (m = 12,0 kg + 7,0 kg) e sua aceleração foi encontrada\(a = 1.5 \, m/s^2 \) no exemplo anterior. Assim,\[F_{net} = ma \nonumber \]

    \[ F_{net} = (19.0 \, kg)(1.5 \, m/s^2) = 29 \, N. \nonumber \]

    Agora podemos encontrar a força desejada:\[ F_{prof} = F_{net} + f, \nonumber \]

    \[F_{prof} = 29 \, N + 24.0 \, N = 53 \, N. \nonumber \]

    Discussão

    É interessante que essa força seja significativamente menor do que a força de 150 N que o professor exerceu para trás no chão. Nem toda essa força de 150 N é transmitida para o carrinho; parte dela acelera o professor.

    A escolha de um sistema é uma etapa analítica importante tanto na resolução de problemas quanto na compreensão completa da física da situação (o que não é necessariamente a mesma coisa).

    EXPLORAÇÕES PHET: LABORATÓRIO DE FORÇA GRAVITACIONAL

    Visualize a força gravitacional que dois objetos exercem um sobre o outro. Altere as propriedades dos objetos para ver como isso muda a força da gravidade.

    Resumo da seção

    • A terceira lei do movimento de Newton representa uma simetria básica na natureza. Ele afirma: Sempre que um corpo exerce uma força sobre um segundo corpo, o primeiro corpo experimenta uma força que é igual em magnitude e oposta em direção à força que o primeiro corpo exerce.
    • Um impulso é uma força de reação que empurra um corpo para frente em resposta a uma força para trás. Foguetes, aviões e carros são empurrados para frente por uma força de reação de empuxo.

    Glossário

    Terceira lei do movimento de Newton
    sempre que um corpo exerce uma força sobre um segundo corpo, o primeiro corpo experimenta uma força que é igual em magnitude e oposta em direção à força que o primeiro corpo exerce
    empuxo
    uma força de reação que empurra um corpo para frente em resposta a uma força para trás; foguetes, aviões e carros são empurrados para frente por uma força de reação de empuxo