3.5: Adição de velocidades
- Page ID
- 194366
Objetivos de
Ao final desta seção, você poderá:
- Aplique os princípios de adição de vetores para determinar a velocidade relativa.
- Explique a importância do observador na medição da velocidade.
Velocidade relativa
Se uma pessoa remar um barco através de um rio que flui rapidamente e tenta ir diretamente para a outra margem, o barco se move diagonalmente em relação à costa, como na Figura\(\displaystyle \PageIndex{1}\). O barco não se move na direção em que está apontado. O motivo, claro, é que o rio leva o barco rio abaixo. Da mesma forma, se um avião pequeno sobrevoa em um forte vento cruzado, às vezes você pode ver que o avião não está se movendo na direção em que está apontado, conforme ilustrado na Figura\(\displaystyle \PageIndex{2}\). O avião está se movendo em linha reta em relação ao ar, mas o movimento da massa de ar em relação ao solo o leva para os lados.

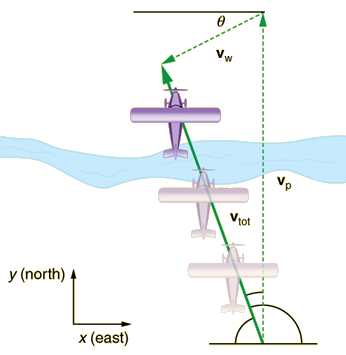
Em cada uma dessas situações, um objeto tem uma velocidade relativa a um meio (como um rio) e esse meio tem uma velocidade em relação a um observador em solo sólido. A velocidade do objeto em relação ao observador é a soma desses vetores de velocidade, conforme indicado nas Figuras\(\displaystyle \PageIndex{1}\)\(\displaystyle \PageIndex{2}\) e. Essas situações são apenas duas das muitas nas quais é útil adicionar velocidades. Neste módulo, primeiro reexaminamos como adicionar velocidades e depois consideramos certos aspectos do que significa velocidade relativa.
Como adicionamos velocidades? A velocidade é um vetor (tem magnitude e direção); as regras de adição vetorial discutidas em Adição e subtração de vetores: métodos gráficos e adição e subtração de vetores: métodos analíticos se aplicam à adição de velocidades, assim como fazem com qualquer outro vetor. Em movimentos unidimensionais, a adição de velocidades é simples — elas somam números comuns. Por exemplo, se uma jogadora de hóquei em campo estiver se movendo a 5 m/s em direção ao gol e dirige a bola na mesma direção com uma velocidade de 30 m/s em relação ao seu corpo, a velocidade da bola é de 35 m/s em relação ao goleiro parado e profusamente suado que está na frente do gol.
Em movimentos bidimensionais, técnicas gráficas ou analíticas podem ser usadas para adicionar velocidades. Vamos nos concentrar em técnicas analíticas. As equações a seguir fornecem as relações entre a magnitude e a direção da velocidade (\(\displaystyle v\)e\(\displaystyle θ\)) e seus componentes (\(\displaystyle v_x\)e\(\displaystyle v_y\)) ao longo dos eixos x e y de um sistema de coordenadas escolhido adequadamente:
\[v_x=v\cos θ\]
\[v_y=v\sin θ\]
\[ v=\sqrt{v^2x+v^2} \]
\[ θ=\tan^{−1}\left(\dfrac{v_y}{v_x}\right).\]
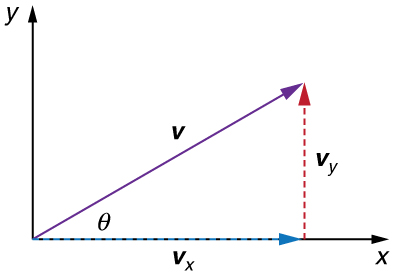
Essas equações são válidas para qualquer vetor e são adaptadas especificamente para velocidade. As duas primeiras equações são usadas para encontrar os componentes de uma velocidade quando sua magnitude e direção são conhecidas. Os dois últimos são usados para encontrar a magnitude e a direção da velocidade quando seus componentes são conhecidos.
EXPERIMENTO PARA LEVAR PARA CASA: VELOCIDADE RELATIVA DE UM BARCO
Encha uma banheira até a metade de água. Pegue um barco de brinquedo ou algum outro objeto que flutue na água. Desconecte o dreno para que a água comece a escorrer. Tente empurrar o barco de um lado da banheira para o outro e perpendicularmente ao fluxo de água. De que maneira você precisa empurrar o barco para que ele acabe imediatamente em frente? Compare as direções do fluxo de água, a direção do barco e a velocidade real do barco.
Exemplo\(\displaystyle \PageIndex{1}\): Adding Velocities - A Boat on a River
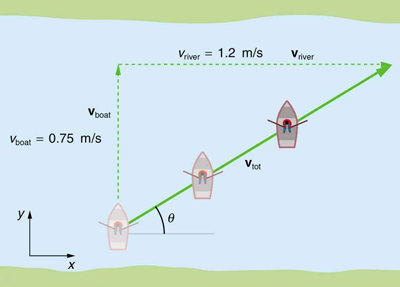
Consulte a Figura\(\displaystyle \PageIndex{4}\), que mostra um barco tentando atravessar o rio em linha reta. Vamos calcular a magnitude e a direção da velocidade do barco em relação a um observador na costa,\(\displaystyle v_{tot}\). A velocidade do barco, vboat, é de 0,75 m/s na direção y em relação ao rio e a velocidade do rio,\(\displaystyle v_{river}\), é de 1,20 m/s à direita.
Estratégia
Começamos escolhendo um sistema de coordenadas com seu\(\displaystyle x\) eixo -paralelo à velocidade do rio, conforme mostrado na Figura. Como o barco é direcionado diretamente para a outra margem, sua velocidade em relação à água é paralela ao eixo y e perpendicular à velocidade do rio. Assim, podemos somar as duas velocidades usando as equações\(\displaystyle v_{tot}=\sqrt{v^2_x+v^2_y}\) e\(\displaystyle θ=tan^{−1}(v_y/v_x)\) diretamente.
Solução
A magnitude da velocidade total é
\(\displaystyle v_{tot}=\sqrt{v^2_x+v^2_y}\),
onde
\(\displaystyle v_x=v_{river}=1.20 m/s\)
e
\(\displaystyle v_y=v_{boat}=0.750 m/s.\)
Assim,
\(\displaystyle v_{tot}=\sqrt{(1.20 m/s)^2+(0.750 m/s)^2}\)
produzindo
\(\displaystyle v_{tot}=1.42 m/s.\)
A direção da velocidade total\(\displaystyle θ\) é dada por:
\(\displaystyle θ=tan^{−1}(v_y/v_x)=tan^{−1}(0.750/1.20).\)
Esta equação fornece
\(\displaystyle θ=32.0º.\)
Discussão
Tanto a magnitude v quanto a direção\(\displaystyle θ\) da velocidade total são consistentes com a Figura. Observe que, como a velocidade do rio é grande em comparação com a velocidade do barco, ele é varrido rapidamente rio abaixo. Esse resultado é evidenciado pelo pequeno ângulo (apenas 32,0º) que a velocidade total tem em relação à margem do rio.
Exemplo\(\displaystyle \PageIndex{2}\): Calculating Velocity - Wind Velocity Causes an Airplane to Drift
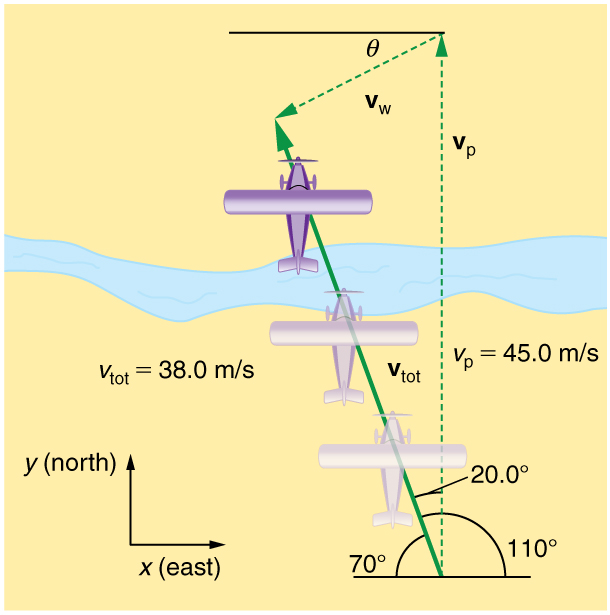
Calcule a velocidade do vento para a situação mostrada na Figura\(\displaystyle \PageIndex{5}\). Sabe-se que o avião está se movendo a 45,0 m/s para o norte em relação à massa de ar, enquanto sua velocidade em relação ao solo (sua velocidade total) é 38,0 m/s na direção 20,0º oeste do norte.
Estratégia
Nesse problema, um pouco diferente do exemplo anterior, sabemos a velocidade total\(\displaystyle v_{to}\) t e que é a soma de duas outras velocidades,\(\displaystyle v_w\) (o vento) e\(\displaystyle v_p\) (o plano em relação à massa de ar). A quantidade\(\displaystyle v_p\) é conhecida e somos convidados a encontrar a vw. Nenhuma das velocidades é perpendicular, mas é possível encontrar seus componentes ao longo de um conjunto comum de eixos perpendiculares. Se pudermos encontrar os componentes do\(\displaystyle v_w\), podemos combiná-los para resolver sua magnitude e direção. Conforme mostrado na Figura, escolhemos um sistema de coordenadas com seu eixo x para o leste e seu eixo y para o norte (paralelo a\(\displaystyle v_p\)). (Você pode relembrar a discussão sobre a adição de vetores usando componentes perpendiculares em Adição e subtração de vetores: métodos analíticos.)
Solução
Como\(\displaystyle v_{tot}\) é a soma vetorial de\(\displaystyle v_w\) e\(\displaystyle v_p\), seus componentes x e y são as somas dos componentes x e y das velocidades do vento e do plano. Observe que o plano tem apenas um componente vertical de velocidade, então\(\displaystyle v_{px}=0\)\(\displaystyle v_{py}=v_p\) e. Ou seja,
\(\displaystyle v_{tot}x=v_{wx}\)
e
\(\displaystyle v_{toty}=v_{wy}+v_p\).
Podemos usar a primeira dessas duas equações para encontrar\(\displaystyle v_{wx}\):
\(\displaystyle v_{wx}=v_{totx}=v_{tot}cos 110º.\)
Porque\(\displaystyle v_{tot}=38.0 m/s\) e\(\displaystyle cos 110º=–0.342\) nós temos
\(\displaystyle v_{wx}=(38.0 m/s)(–0.342)=–13 m/s.\)
O sinal de menos indica movimento para oeste, o que é consistente com o diagrama.
Agora, para encontrar,\(\displaystyle v_{wy}\) notamos que
\(\displaystyle v_{toty}=v_{wy}+v_p\)
Aqui\(\displaystyle v_{toty}=v_{tot}sin 110º\); portanto,
\(\displaystyle v_{wy}=(38.0 m/s)(0.940)−45.0 m/s=−9.29 m/s.\)
Esse sinal de menos indica movimento para o sul, o que é consistente com o diagrama.
Agora que os componentes perpendiculares da velocidade\(\displaystyle v_{wx}\) do vento\(\displaystyle v_{wy}\) são conhecidos, podemos encontrar a magnitude e a direção de\(\displaystyle v_w\). Primeiro, a magnitude é
\(\displaystyle v_w=\sqrt{v^2_{wx}+v^2_{wy}}=\sqrt{(−13.0 m/s)^2+(−9.29 m/s)^2}\)
para que
\(\displaystyle v_w=16.0 m/s.\)
A direção é:
\(\displaystyle θ=tan^{−1}(v_{wy}/v_{wx})=tan^{−1}(−9.29/−13.0)\)
dando
\(\displaystyle θ=35.6º.\)
Discussão
A velocidade e a direção do vento são consistentes com o efeito significativo que o vento tem na velocidade total do avião, conforme visto na Figura. Como o avião está lutando contra uma forte combinação de vento cruzado e vento frontal, ele acaba com uma velocidade total significativamente menor do que sua velocidade em relação à massa de ar, além de seguir em uma direção diferente.
Observe que nos dois últimos exemplos, conseguimos facilitar a matemática escolhendo um sistema de coordenadas com um eixo paralelo a uma das velocidades. Descobriremos repetidamente que escolher um sistema de coordenadas apropriado facilita a solução de problemas. Por exemplo, no movimento de projéteis, sempre usamos um sistema de coordenadas com um eixo paralelo à gravidade.
Velocidades relativas e relatividade clássica
Ao adicionar velocidades, tivemos o cuidado de especificar que a velocidade é relativa a algum quadro de referência. Essas velocidades são chamadas de velocidades relativas. Por exemplo, a velocidade de um avião em relação a uma massa de ar é diferente de sua velocidade em relação ao solo. Ambos são bem diferentes da velocidade de um avião em relação aos seus passageiros (que deve estar perto de zero). As velocidades relativas são um aspecto da relatividade, que é definido como o estudo de como diferentes observadores que se movem em relação um ao outro medem o mesmo fenômeno.
Quase todo mundo já ouviu falar da relatividade e imediatamente a associa a Albert Einstein (1879-1955), o maior físico do século XX. Einstein revolucionou nossa visão da natureza com sua moderna teoria da relatividade, que estudaremos em capítulos posteriores. As velocidades relativas nesta seção são, na verdade, aspectos da relatividade clássica, discutidos pela primeira vez corretamente por Galileu e Isaac Newton. A relatividade clássica é limitada a situações em que as velocidades são inferiores a cerca de 1% da velocidade da luz, ou seja, menores que. A maioria das coisas que encontramos na vida diária se move mais devagar do que essa velocidade.
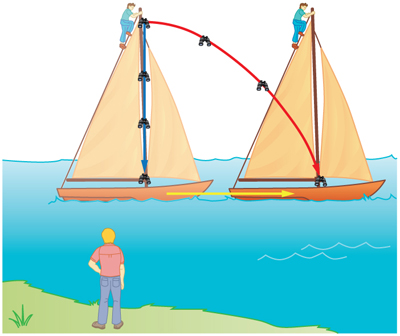
Vamos considerar um exemplo do que dois observadores diferentes veem em uma situação analisada há muito tempo por Galileu. Suponha que um marinheiro no topo de um mastro em um navio em movimento solte seus binóculos. Onde vai chegar ao convés? Ele atingirá a base do mastro ou atingirá atrás do mastro porque o navio está avançando? A resposta é que, se a resistência do ar for insignificante, os binóculos atingirão a base do mastro em um ponto diretamente abaixo do ponto de liberação. Agora, vamos considerar o que dois observadores diferentes veem quando os binóculos caem. Um observador está no navio e o outro na costa. Os binóculos não têm velocidade horizontal em relação ao observador no navio, e então ele os vê cair diretamente no mastro. (Figura\(\displaystyle \PageIndex{1}\); curva azul) Para o observador em terra, os binóculos e o navio têm a mesma velocidade horizontal, então ambos se movem na mesma distância para frente enquanto os binóculos estão caindo. Este observador vê o caminho curvo vermelho mostrado na Figura\(\displaystyle \PageIndex{6}\). Embora os caminhos pareçam diferentes para os diferentes observadores, cada um vê o mesmo resultado: os binóculos batem na base do mastro e não atrás dele. Para obter a descrição correta, é crucial especificar corretamente as velocidades em relação ao observador.
Exemplo\(\displaystyle \PageIndex{3}\): Calculating Relative Velocity: An Airline Passenger Drops a Coin
Um passageiro da companhia aérea deixa cair uma moeda enquanto o avião está se movendo a 260 m/s. Qual é a velocidade da moeda quando ela atinge o chão 1,50 m abaixo do ponto de lançamento: (a) Medida em relação ao avião? (b) Medido em relação à Terra?
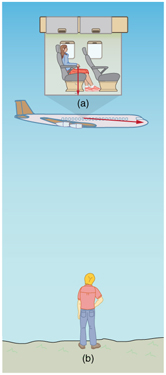
Estratégia
Ambos os problemas podem ser resolvidos com as técnicas de queda de objetos e projéteis. Na parte (a), a velocidade inicial da moeda é zero em relação ao plano, então o movimento é o de um objeto caindo (unidimensional). Na parte (b), a velocidade inicial é de 260 m/s na horizontal em relação à Terra e a gravidade é vertical, então esse movimento é um movimento de projétil. Em ambas as partes, é melhor usar um sistema de coordenadas com eixos vertical e horizontal.
Solução para (a)
Usando as informações fornecidas, notamos que a velocidade e a posição iniciais são zero e a posição final é 1,50 m. A velocidade final pode ser encontrada usando a equação:
\(\displaystyle v_y^2=v_{0y}^2−2g(y−y_0).\)
Substituindo valores conhecidos na equação, obtemos
\(\displaystyle v_y^2=0^2−2(9.80m/s^2)(−1.50m−0 m)=29.4m^2/s^2\)
produzindo
\(\displaystyle v_y=−5.42 m/s.\)
Sabemos que a raiz quadrada de 29,4 tem duas raízes: 5,42 e -5,42. Escolhemos a raiz negativa porque sabemos que a velocidade é direcionada para baixo e definimos a direção positiva como ascendente. Não há velocidade horizontal inicial em relação ao plano e nenhuma aceleração horizontal e, portanto, o movimento é direto para baixo em relação ao plano.
Solução para (b)
Como a velocidade vertical inicial é zero em relação ao solo e o movimento vertical é independente do movimento horizontal, a velocidade vertical final da moeda em relação ao solo é\(\displaystyle v_y=−5.42m/s\) a mesma encontrada na parte (a). Em contraste com a parte (a), agora existe um componente horizontal da velocidade. No entanto, como não há aceleração horizontal, as velocidades horizontais inicial e final são as mesmas\(\displaystyle v_x=260 m/s\) e. Os componentes x e y da velocidade podem ser combinados para encontrar a magnitude da velocidade final:
\(\displaystyle v=\sqrt{v_x^2+v_y^2}\).
Assim,
\(\displaystyle v=\sqrt{(260 m/s)^2+(−5.42 m/s)^2}\)
produzindo
\(\displaystyle v=260.06 m/s.\)
A direção é dada por:
\(\displaystyle θ=tan^{−1}(v_y/v_x)=tan^{−1}(−5.42/260)\)
para que
\(\displaystyle θ=tan^{−1}(−0.0208)=−1.19º.\)
Discussão
Na parte (a), a velocidade final em relação ao avião é a mesma que seria se a moeda caísse do repouso na Terra e caísse 1,50 m. Esse resultado se encaixa em nossa experiência; objetos em um avião caem da mesma forma quando o avião está voando horizontalmente e quando está em repouso no solo. Esse resultado também é verdadeiro em carros em movimento. Na parte (b), um observador no chão vê um movimento muito diferente para a moeda. O avião está se movendo tão rápido horizontalmente para começar que sua velocidade final é pouco maior que a velocidade inicial. Mais uma vez, vemos que em duas dimensões, os vetores não somam como números comuns — a velocidade final v na parte (b) não é\(\displaystyle (260 – 5.42) m/s\); em vez disso, é.\(\displaystyle 260.06 m/s.\) A magnitude da velocidade teve que ser calculada para cinco dígitos para ver qualquer diferença em relação à do avião. Os movimentos vistos por diferentes observadores (um no avião e outro no solo) neste exemplo são análogos aos discutidos para os binóculos lançados do mastro de uma nave em movimento, exceto que a velocidade do avião é muito maior, de modo que os dois observadores veem caminhos muito diferentes. (Veja a Figura.) Além disso, os dois observadores veem a moeda cair 1,50 m na vertical, mas a moeda no chão também a vê avançar 144 m (esse cálculo é deixado para o leitor). Assim, um observador vê um caminho vertical, o outro um caminho quase horizontal.
FAZENDO CONEXÕES: RELATIVIDADE E EINSTEIN
Como Einstein conseguiu definir claramente como as medições são feitas (algumas envolvem luz) e como a velocidade da luz é a mesma para todos os observadores, os resultados são espetacularmente inesperados. O tempo varia com o observador, a energia é armazenada à medida que a massa aumenta e mais surpresas aguardam.
EXPLORAÇÕES PHET: MOVIMENTO EM 2D
Experimente a nova simulação “Ladybug Motion 2D” para obter a versão atualizada mais recente. Saiba mais sobre vetores de posição, velocidade e aceleração. Mova a bola com o mouse ou deixe a simulação mover a bola em quatro tipos de movimento (2 tipos de movimento linear, harmônico simples, circular).

Resumo
- Velocidades em duas dimensões são adicionadas usando as mesmas técnicas de vetores analíticos, que são reescritas como
\(\displaystyle v_x=vcosθ\)
\(\displaystyle v_y=vsinθ\)
\(\displaystyle v=\sqrt{v^2_x+v^2+y}\)
\(\displaystyle θ=tan^{−1}(v_y/v_x)\).
- A velocidade relativa é a velocidade de um objeto observada a partir de um determinado quadro de referência e varia dramaticamente com o quadro de referência.
- A relatividade é o estudo de como diferentes observadores medem o mesmo fenômeno, particularmente quando os observadores se movem em relação um ao outro. A relatividade clássica é limitada a situações em que a velocidade é inferior a cerca de 1% da velocidade da luz (3000 km/s).
Glossário
- relatividade clássica
- o estudo das velocidades relativas em situações em que as velocidades são inferiores a cerca de 1% da velocidade da luz, ou seja, menos de 3000 km/s
- velocidade relativa
- a velocidade de um objeto observada a partir de um determinado quadro de referência
- relatividade
- o estudo de como diferentes observadores que se movem em relação uns aos outros medem o mesmo fenômeno
- velocidade
- velocidade em uma determinada direção
- adição de vetores
- as regras que se aplicam à adição de vetores


