3.E: Cinemática bidimensional (exercícios)
- Page ID
- 194376
Perguntas conceituais
3.2: Adição e subtração de vetores: métodos gráficos
1. Qual das seguintes opções é um vetor: a altura de uma pessoa, a altitude no Monte. Everest, a idade da Terra, o ponto de ebulição da água, o custo deste livro, a população da Terra, a aceleração da gravidade?
2. Dê um exemplo específico de um vetor, declarando sua magnitude, unidades e direção.
3. O que vetores e escalares têm em comum? Como eles diferem?
4. Dois campistas em um parque nacional caminham de sua cabana até o mesmo local em um lago, cada um seguindo um caminho diferente, conforme ilustrado abaixo. A distância total percorrida ao longo do Caminho 1 é de 7,5 km, e ao longo do Caminho 2 é de 8,2 km. Qual é o deslocamento final de cada trailer?
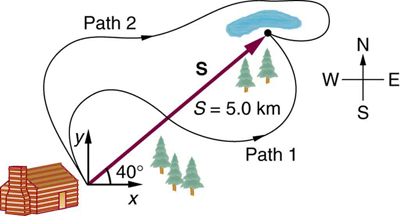
5. Se um piloto de avião for instruído a voar 123 km em linha reta para ir de São Francisco a Sacramento, explique por que ele pode acabar em qualquer lugar do círculo mostrado na Figura. Que outras informações ele precisaria para chegar a Sacramento?
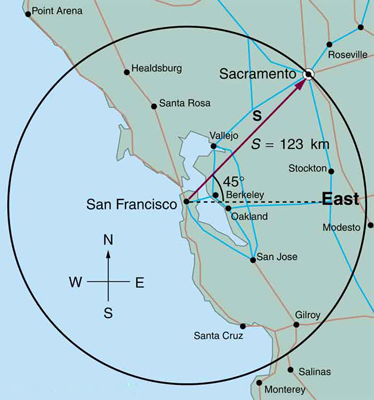
6. Suponha que você dê dois passos A e B (ou seja, dois deslocamentos diferentes de zero). Sob quais circunstâncias você pode acabar no seu ponto de partida? De forma mais geral, sob quais circunstâncias dois vetores diferentes de zero podem ser adicionados para dar zero? A distância máxima que você pode chegar do ponto de partida A+B é a soma dos comprimentos dos dois degraus?
7. Explique por que não é possível adicionar um escalar a um vetor
8. Se você seguir duas etapas de tamanhos diferentes, você pode acabar no ponto de partida? De forma mais geral, dois vetores com magnitudes diferentes podem chegar a zero? Podem três ou mais?
3.3: Adição e subtração de vetores: métodos analíticos
9. Suponha que você adicione dois vetores A e B. Qual direção relativa entre eles produz a resultante com a maior magnitude? Qual é a magnitude máxima? Qual direção relativa entre eles produz a resultante com a menor magnitude? Qual é a magnitude mínima?
10. Dê um exemplo de um vetor diferente de zero que tem um componente de zero.
11. Explique por que um vetor não pode ter um componente maior que sua própria magnitude.
12. Se os vetores A e B são perpendiculares, qual é o componente de A na direção de B? Qual é o componente de B na direção de A?
3.4: Movimento do projétil
13. Responda às seguintes perguntas para o movimento do projétil em solo nivelado, assumindo uma resistência de ar insignificante (o ângulo inicial não é nem 0º nem 90º):
(a) A velocidade é sempre zero?
(b) Quando a velocidade é mínima? Um máximo?
(c) A velocidade pode ser a mesma que a velocidade inicial em um momento diferente de at\(t=0\)?
(d) A velocidade pode ser a mesma que a velocidade inicial em um momento diferente de em\(t=0\)?
14. Responda às seguintes perguntas sobre o movimento do projétil em solo nivelado, assumindo uma resistência insignificante do ar (o ângulo inicial é\(0º\) nenhum dos dois\(90º\)):
(a) A aceleração é sempre zero?
(b) A aceleração está sempre na mesma direção de um componente da velocidade?
(c) A aceleração é sempre oposta em direção a um componente da velocidade?
15. Para uma velocidade inicial fixa, o alcance de um projétil é determinado pelo ângulo em que ele é disparado. Para todos, exceto o máximo, existem dois ângulos que fornecem o mesmo alcance. Considerando os fatores que podem afetar a capacidade de um arqueiro atingir um alvo, como o vento, explique por que o ângulo menor (mais próximo da horizontal) é preferível. Quando seria necessário que o arqueiro usasse o ângulo maior? Por que o apostador em um jogo de futebol usa a trajetória mais alta?
16. Durante uma palestra demonstrativa, um professor coloca duas moedas na borda de uma mesa. Ela então joga uma das moedas horizontalmente para fora da mesa, empurrando simultaneamente a outra para a borda. Descreva o movimento subsequente das duas moedas, em particular discutindo se elas caem no chão ao mesmo tempo.
3.5: Adição de velocidades
17. Que quadro ou quadros de referência você usa instintivamente ao dirigir um carro? Ao voar em um avião a jato comercial?
18. Um jogador de basquete que dribla pela quadra geralmente mantém os olhos fixos nos jogadores ao seu redor. Ele está se movendo rápido. Por que ele não precisa manter os olhos na bola?
19. Se alguém estiver andando na traseira de uma caminhonete e jogar uma bola de softball para trás, é possível que a bola caia diretamente, conforme vista por uma pessoa parada na beira da estrada? Em que condições isso ocorreria? Como o movimento da bola apareceria para a pessoa que a jogou?
20. O chapéu de um corredor correndo em velocidade constante cai da nuca. Desenhe um esboço mostrando o caminho do chapéu no quadro de referência do corredor. Desenhe seu caminho conforme visto por um observador estacionário.
21. Um pedaço de terra cai da caçamba de um caminhão em movimento. Ele atinge o solo diretamente abaixo da extremidade do caminhão. Qual é a direção de sua velocidade em relação ao caminhão logo antes de bater? Isso é o mesmo que a direção de sua velocidade em relação ao solo logo antes de atingir? Explique suas respostas.
Problemas e exercícios
3.2: Adição e subtração de vetores: métodos gráficos
Use métodos gráficos para resolver esses problemas. Você pode presumir que os dados retirados dos gráficos têm precisão de três dígitos.
22. Encontre o seguinte para o caminho A na Figura:
(a) a distância total percorrida, e
(b) a magnitude e a direção do deslocamento do início ao fim.
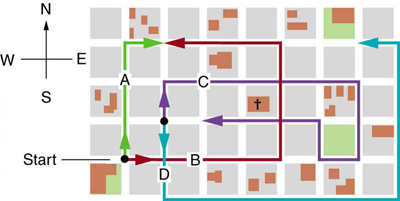
As várias linhas representam caminhos percorridos por diferentes pessoas caminhando em uma cidade. Todos os blocos têm 120 m de lado.
solução:
(a) 480 m
(b) 379 m, 18,4º a leste do norte
23. Encontre o seguinte para o caminho B na Figura:
(a) a distância total percorrida, e
(b) a magnitude e a direção do deslocamento do início ao fim.
24. Encontre os componentes norte e leste do deslocamento para os caminhantes mostrados na Figura.

Componente
norte da solução 3,21 km, componente leste 3,83 km
25. Suponha que você ande 18,0 m em linha reta para o oeste e depois 25,0 m para o norte. A que distância você está do ponto de partida e qual é a direção da bússola de uma linha conectando seu ponto de partida à sua posição final? (Se você representar as duas pernas da caminhada como deslocamentos vetoriais A e B, como na Figura, esse problema solicitará que você encontre a soma R=A+B.)
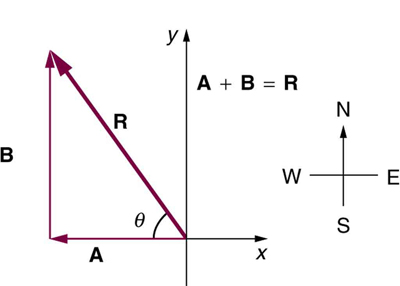
Os dois deslocamentos A e B se somam para dar um deslocamento total R com magnitude\(R\) e direção\(θ\).
26. Suponha que você caminhe primeiro 12,0 m em uma direção 20º a oeste do norte e depois 20,0 m na direção 40,0º ao sul de oeste. A que distância você está do ponto de partida e qual é a direção da bússola de uma linha conectando seu ponto de partida à sua posição final? (Se você representar as duas pernas da caminhada como deslocamentos vetoriais A e B, como na Figura, esse problema encontra sua soma R = A + B.)
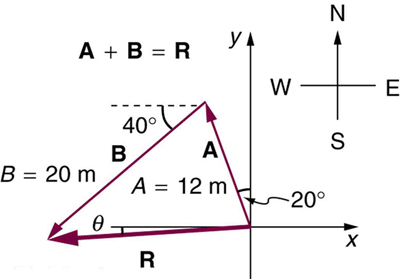
Solução
\(19.5 m, 4.65º\) sul ou oeste
27. Repita o problema acima, mas inverta a ordem das duas pernas da caminhada; mostre que você obtém o mesmo resultado final. Ou seja, você primeiro anda a perna B, que é 20,0 m em uma direção exatamente 40º ao sul de oeste, e depois a perna A tamanho 12 {A} {}, que é 12,0 m em uma direção exatamente 20º a oeste do norte. (Esse problema mostra que A+B=B+A.)
28. (a) Repita o problema dois problemas anteriores, mas para a segunda etapa você anda 20,0 m em uma direção 40,0º ao norte do leste (o que equivale a subtrair B de A, ou seja, encontrar R'=A−B).
(b) Repita o problema dois problemas anteriores, mas agora você caminha primeiro 20,0 m em uma direção 40,0º ao sul de oeste e depois 12,0 m em uma direção 20,0º a leste do sul (o que equivale a subtrair A de B —isto é, encontrar R"=B−A=−R'). Mostre que esse é o caso.
Solução
(a)\(26.6 m, 65.1º\) norte de leste
(b)\(26.6 m, 65.1º\) sul de oeste
29. Mostre que a ordem de adição de três vetores não afeta sua soma. Mostre essa propriedade escolhendo quaisquer três vetores A, B e C, todos com comprimentos e direções diferentes. Encontre a soma A + B + C e encontre sua soma quando adicionada em uma ordem diferente e mostre que o resultado é o mesmo. (Há outras cinco ordens nas quais A, B e C podem ser adicionadas; escolha apenas uma.)
30. Mostre que a soma dos vetores discutidos no Exemplo fornece o resultado mostrado na Figura.
Solução em
\(52.9 m, 90.1º\) relação ao eixo x.
31. Encontre as magnitudes das velocidades\(v_A\) e\(v_B\) na Figura
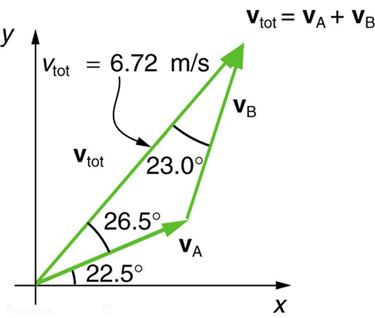
As duas velocidades\(v_A\) e o\(v_B\) acréscimo para dar um total\(v_{tot}\).
32. Encontre os componentes do\(v_{tot}\) ao longo dos eixos x e y na Figura.
Componente x da solução 4,41 m/s
componente y 5,07 m/s
33. Encontre os componentes\(v_{tot}\) ao longo de um conjunto de eixos perpendiculares girados\(30º\) no sentido anti-horário em relação aos da Figura.
3.3: Adição e subtração de vetores: métodos analíticos
34. Encontre o seguinte para o caminho C na Figura:
(a) a distância total percorrida e
(b) a magnitude e a direção do deslocamento do início ao fim. Nesta parte do problema, mostre explicitamente como você segue as etapas do método analítico de adição vetorial.

As várias linhas representam caminhos percorridos por diferentes pessoas caminhando em uma cidade. Todos os blocos têm 120 m de lado.
Solução
(a) 1,56 km
(b) 120 km a leste
35. Encontre o seguinte para o caminho D na Figura:
(a) a distância total percorrida e
(b) a magnitude e a direção do deslocamento do início ao fim. Nesta parte do problema, mostre explicitamente como você segue as etapas do método analítico de adição vetorial.
36. Encontre os componentes norte e leste do deslocamento de São Francisco para Sacramento, mostrados na Figura.

Solução
Componente Norte 87,0 km, componente leste 87,0 km
37. Resolva o seguinte problema usando técnicas analíticas: Suponha que você caminhe 18,0 m em linha reta para o oeste e depois 25,0 m em linha reta para o norte. A que distância você está do ponto de partida e qual é a direção da bússola de uma linha conectando seu ponto de partida à sua posição final? (Se você representar as duas pernas da caminhada como deslocamentos vetoriais A e B, como na Figura, esse problema solicitará que você encontre a soma R=A+B.)

Os dois deslocamentos A e B se somam para dar um deslocamento total R com magnitude\(R\) e direção\(θ\).
Observe que você também pode resolver isso graficamente. Discuta por que a técnica analítica para resolver esse problema é potencialmente mais precisa do que a técnica gráfica.
38. Repita o exercício usando técnicas analíticas, mas inverta a ordem das duas pernas da caminhada e mostre que você obtém o mesmo resultado final. (Esse problema mostra que adicioná-los na ordem inversa dá o mesmo resultado, ou seja, B + A = A + B.) Discuta como seguir outro caminho para chegar ao mesmo ponto pode ajudar a superar um obstáculo que bloqueia seu outro caminho.
Solução
30,8 km, 35,8 a oeste do norte
Você dirige 7,50 km em linha reta na direção de 15º.
(a) Encontre as distâncias que você teria que dirigir direto para o leste e depois para o norte para chegar ao mesmo ponto. (Essa determinação é equivalente a encontrar os componentes do deslocamento ao longo das direções leste e norte.)
(b) Mostre que você ainda chega ao mesmo ponto se as pernas leste e norte estiverem invertidas em ordem.
39. a) Faça exercícios novamente usando técnicas analíticas e mude a segunda etapa da caminhada para 25,0 m em linha reta para o sul. (Isso é equivalente a subtrair B de A —isto é, encontrar R'=A — B)
(b) Repita novamente, mas agora você primeiro anda 25,0 m tamanho 12 {"25" “.” “0 m"} {} norte e depois 18,0 m tamanho 12 {"18" “.” “0 m"} {} leste. (Isso equivale a subtrair A tamanho 12 {A} {} do tamanho B 12 {B} {} — ou seja, encontrar A=B+C tamanho 12 {A=B+C} {}. Isso é consistente com seu resultado?)
Solução
(a)\(30.8 m, 54.2º\) sul de oeste
(b)\(30.8 m, 54.2º\) norte de leste
40. Um novo proprietário de terras tem um pedaço triangular de terra plana que ela deseja cercar. Começando no canto oeste, ela mede o primeiro lado com 80,0 m de comprimento e o próximo com 105 m. Esses lados são representados como vetores de deslocamento A de B na Figura. Ela então calcula corretamente o comprimento e a orientação do terceiro lado\(C\). Qual é o resultado dela?
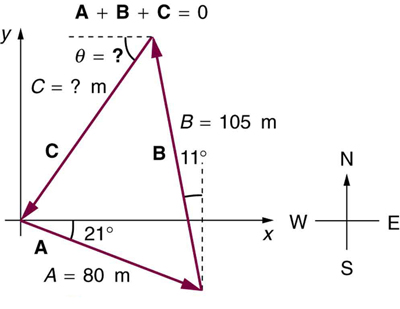
41. Você voa 32,0 km tamanho 12 {"32" “.” “0 km"} {} em linha reta no ar parado na direção 35,0º tamanho 12 {"35"°} {} sul do oeste.
(a) Encontre as distâncias que você teria que voar direto para o sul e depois para o oeste para chegar ao mesmo ponto. (Essa determinação é equivalente a encontrar os componentes do deslocamento nas direções sul e oeste.)
(b) Encontre as distâncias que você teria que voar primeiro na direção 45,0º ao sul do oeste e depois na direção 45,0º oeste do norte. Esses são os componentes do deslocamento ao longo de um conjunto diferente de eixos — um girado em 45º.
Solução
18,4 km ao sul, depois 26,2 km a oeste (b) 31,5 km a 45,0º ao sul de oeste, depois 5,56 km a 45,0º oeste do norte
42. Um fazendeiro quer cercar seu terreno plano de quatro lados. Ele mede os três primeiros lados, mostrados como A, B e C na Figura, e então calcula corretamente o comprimento e a orientação do quarto lado\(D\). Qual é o resultado dele?
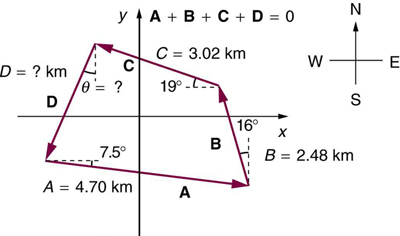
43. Na tentativa de escapar de sua ilha, Gilligan constrói uma balsa e parte para o mar. O vento muda muito durante o dia, e ele é levado pelas seguintes linhas retas: 2,50 km 45,0º ao norte de oeste; depois 4,70 km 60,0º ao sul de leste; depois 1,30 km 25,0º ao sul de oeste; depois 5,10 km em linha reta leste; depois 1,70 km 5,00º a leste de norte; depois 7,20 km 55,0º ao sul de oeste; e finalmente 2,80 km 10,0º ao norte de leste. Qual é a posição final dele em relação à ilha?
Solução
\(7.34 km, 63.5º\) sul do leste
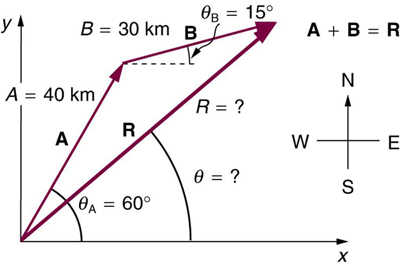
44. Suponha que um piloto voe 40,0 km em uma direção 60º ao norte do leste e depois voe 30,0 km em uma direção 15º ao norte do leste, conforme mostrado na Figura. Encontre sua distância total\(R\) do ponto de partida e a direção\(θ\) do caminho em linha reta até a posição final. Discuta qualitativamente como esse voo seria alterado por um vento do norte e como o efeito do vento dependeria tanto da velocidade do vento quanto da velocidade do avião em relação à massa de ar.
3.4: Movimento do projétil
45. Um projétil é lançado no nível do solo com uma velocidade inicial de 50,0 m/s em um ângulo de 30,0º acima da horizontal. Ele atinge um alvo acima do solo 3,00 segundos depois. Quais são as\(y\) distâncias\(x\) e as distâncias de onde o projétil foi lançado até onde ele pousa?
Solução
\(x=1.30 m×10%2\)
\(y=30.9 m.\)
46. Uma bola é chutada com uma velocidade inicial de 16 m/s na direção horizontal e 12 m/s na direção vertical.
(a) A que velocidade a bola atinge o chão?
(b) Por quanto tempo a bola permanece no ar?
(c) Qual altura máxima é atingida pela bola?
47. Uma bola é lançada horizontalmente do topo de um prédio de 60,0 m e cai a 100,0 m da base do prédio. Ignora a resistência do ar
(a) Quanto tempo a bola fica no ar?
(b) Qual deve ter sido o componente horizontal inicial da velocidade?
(c) Qual é o componente vertical da velocidade logo antes da bola atingir o solo? (d) Qual é a velocidade (incluindo os componentes horizontal e vertical) da bola logo antes de atingir o solo?
Solução
(a) 3,50 s
(b) 28,6 m/s
(c) 34,3 m/s
(d) 44,7 m/s, 50,2º abaixo da horizontal
48. (a) Um temerário está tentando pular sua moto sobre uma linha de ônibus estacionados de ponta a ponta subindo uma rampa de 32º a uma velocidade de 40,0 m/s (144 km/h). Quantos ônibus ele pode limpar se o topo da rampa de decolagem estiver na mesma altura dos pontos de ônibus e os ônibus tiverem 20,0 m de comprimento?
(b) Discuta o que sua resposta implica sobre a margem de erro neste ato, ou seja, considere quanto maior é o alcance do que a distância horizontal que ele deve percorrer para perder o final do último ônibus. (Negligencie a resistência do ar.)
49. Um arqueiro atira uma flecha em um alvo distante de 75,0 m; o alvo está na mesma altura que a altura de lançamento da flecha.
(a) Em que ângulo a flecha deve ser liberada para atingir o alvo se sua velocidade inicial for de 35,0 m/s? Nesta parte do problema, mostre explicitamente como você segue as etapas envolvidas na solução de problemas de movimento de projéteis.
(b) Há uma grande árvore a meio caminho entre o arqueiro e o alvo com um galho horizontal pendente 3,50 m acima da altura de lançamento da flecha. A flecha passará por cima ou por baixo do galho?
Solução
(a) 18,4º
(b) A seta passará por cima do galho.
50. Um jogador de rúgbi passa a bola 7,00 m pelo campo, onde ela é pega na mesma altura em que deixou a mão.
(a) Em que ângulo a bola foi lançada se sua velocidade inicial fosse de 12,0 m/s, assumindo que o menor dos dois ângulos possíveis foi usado?
(b) Que outro ângulo fornece o mesmo alcance e por que não seria usado?
(c) Quanto tempo demorou esse passe?
51. Verifique os intervalos dos projéteis na Figura (a)\(θ=45º\) e as velocidades iniciais fornecidas.
Solução
\(R=\frac{v^2_0}{sin2θ_0g}\)
para\(θ=45º,R=\frac{v^2_0}{g}\)
\(R=91.8m\) para\(v_0=30m/s; R=163m\) para\(v_0=40m/s; R=255m\) para\(v_=50m/s\).
52. Verifique os intervalos mostrados para os projéteis na Figura (b) para uma velocidade inicial de 50 m/s nos ângulos iniciais fornecidos.
53. O canhão em um navio de guerra pode disparar um projétil a uma distância máxima de 32,0 km.
(a) Calcule a velocidade inicial do projétil.
(b) Qual a altura máxima que atinge? (No máximo, a concha está acima de 60% da atmosfera, mas a resistência do ar não é realmente insignificante, como se supõe que torne esse problema mais fácil.)
(c) O oceano não é plano, porque a Terra é curva. Suponha que o raio da Terra seja\(6.37×10^3km\). Quantos metros abaixo sua superfície estará a 32,0 km do navio ao longo de uma linha horizontal paralela à superfície do navio? Sua resposta implica que o erro introduzido pela suposição de uma Terra plana em movimento de projétil é significativo aqui?
Solução
(a) 560 m/s
(b)\(8.00×10^3m\)
(c) 80,0 m. Esse erro não é significativo porque representa apenas 1% da resposta na parte (b).
54. Uma flecha é disparada de uma altura de 1,5 m em direção a um penhasco de altura\(H\) tamanho 12 {H} {}. É filmado com uma velocidade de 30 m/s em um ângulo de 60º acima da horizontal. Ele pousa na borda superior do penhasco 4.0 s depois.
(a) Qual é a altura do penhasco?
(b) Qual é a altura máxima alcançada pela flecha ao longo de sua trajetória?
(c) Qual é a velocidade de impacto da flecha logo antes de atingir o penhasco?
55. No salto largo em pé, a pessoa se agacha e depois empurra com as pernas para ver até onde se pode pular. Suponha que a extensão das pernas da posição agachada seja de 0,600 m e a aceleração alcançada nessa posição seja 1,25 vezes a aceleração devido à gravidade,\(g\) tamanho 12 {g} {}. Até onde eles podem pular? Exponha suas suposições. (O alcance aumentado pode ser alcançado balançando os braços na direção do salto.)
Solução
1,50 m, assumindo um ângulo de lançamento de 45º
56. O recorde mundial de salto em distância é de 8,95 m (Mike Powell, EUA, 1991). Tratado como um projétil, qual é o alcance máximo que uma pessoa pode obter se ela tiver uma velocidade de decolagem de 9,5 m/s? Exponha suas suposições.
57. Servindo a uma velocidade de 170 km/h, um tenista bate na bola a uma altura de 2,5 m e um ângulo\(θ\) abaixo da horizontal. A linha de base fica a 11,9 m da rede, que tem 0,91 m de altura. Qual é o ângulo\(θ\) em que a bola simplesmente cruza a rede? A bola cairá na caixa de serviço, cuja linha de serviço fica a 6,40 m da rede?
Solução
\(θ=6.1º\)
: sim, a bola cai a 5,3 m da rede
58. Um zagueiro de futebol está se movendo para trás a uma velocidade de 2,00 m/s quando lança um passe para um jogador de 18,0 m direto no campo.
(a) Se a bola for lançada em um ângulo de 25º em relação ao solo e for presa na mesma altura em que é lançada, qual é sua velocidade inicial em relação ao solo?
(b) Quanto tempo leva para chegar ao receptor?
(c) Qual é sua altura máxima acima do ponto de liberação?
59. A mira do canhão é ajustada para mirar alto para compensar o efeito da gravidade, tornando a arma precisa apenas para um alcance específico.
(a) Se uma arma atingir alvos que estejam na mesma altura do canhão e a 100,0 m de distância, até que ponto a bala atingirá se apontada diretamente para um alvo a 150,0 m de distância? A velocidade do cano da bala é de 275 m/s.
(b) Discuta qualitativamente como uma maior velocidade do focinho afetaria esse problema e qual seria o efeito da resistência do ar.
Solução
(a) −0,486 m
(b) Quanto maior a velocidade do focinho, menor o desvio na direção vertical, pois o tempo de voo seria menor. A resistência do ar teria o efeito de diminuir o tempo de voo, aumentando assim o desvio vertical.
60. Uma águia está voando horizontalmente a uma velocidade de 3,00 m/s quando o peixe em suas garras se solta e cai no lago 5,00 m abaixo. Calcule a velocidade do peixe em relação à água quando ele atinge a água.
61. Uma coruja está carregando um rato até os filhotes em seu ninho. Sua posição naquele momento é de 4,00 m a oeste e 12,0 m acima do centro do ninho de 30,0 cm de diâmetro. A coruja está voando para o leste a 3,50 m/s em um ângulo de 30,0º tamanho 12 {"30º} abaixo da horizontal quando acidentalmente deixa cair o mouse. A coruja tem a sorte de ter o rato batendo no ninho? Para responder a essa pergunta, calcule a posição horizontal do mouse quando ele cair 12,0 m.
Solução
4,23 m. Não, a coruja não tem sorte; ele perde o ninho.
62. Suponha que um jogador de futebol chute a bola a uma distância de 30 m em direção ao gol. Determine a velocidade inicial da bola se ela passar por cima do gol, 2,4 m acima do solo, desde que a direção inicial seja 40º acima da horizontal.
63. Um goleiro em seu gol pode chutar uma bola de futebol para o gol do adversário sem que a bola toque o chão? A distância será de cerca de 95 m. Um goleiro pode dar à bola uma velocidade de 30 m/s.
Solução
Não, o alcance máximo (negligenciando a resistência do ar) é de cerca de 92 m.
64. A linha de lance livre no basquete está a 4,57 m (15 pés) da cesta, que fica a 3,05 m (10 pés) acima do chão. Um jogador que está na linha de lance livre lança a bola com uma velocidade inicial de 8,15 m/s, soltando-a a uma altura de 2,44 m (8 pés) acima do chão. Em que ângulo acima da horizontal a bola deve ser lançada para atingir exatamente a cesta? Observe que a maioria dos jogadores usará um ângulo inicial grande em vez de um tiro plano, pois isso permite uma margem de erro maior. Mostre explicitamente como você segue as etapas envolvidas na solução de problemas de movimento de projéteis.
65. Em 2007, Michael Carter (EUA) estabeleceu um recorde mundial no arremesso de peso com um arremesso de 24,77 m. Qual era a velocidade inicial do tiro se ele o lançasse a uma altura de 2,10 m e o lançasse em um ângulo de 38,0º acima da horizontal? (Embora a distância máxima de um projétil em terreno nivelado seja alcançada em 45º quando a resistência do ar é negligenciada, o ângulo real para atingir o alcance máximo é menor; portanto, 38º fornecerá um alcance maior do que 45º no arremesso de peso.)
Solução
15,0 m/s
66. Um jogador de basquete está correndo a 5,00 m/s diretamente em direção à cesta quando ele pula no ar para enterrar a bola. Ele mantém sua velocidade horizontal.
(a) Qual velocidade vertical ele precisa para subir 0,750 m acima do chão?
(b) A que distância da cesta (medida na direção horizontal) ele deve iniciar seu salto para atingir sua altura máxima ao mesmo tempo em que alcança a cesta?
67. Um jogador de futebol lança a bola em um ângulo de 45,0º. Sem um efeito do vento, a bola percorreria 60,0 m na horizontal.
(a) Qual é a velocidade inicial da bola?
(b) Quando a bola está perto de sua altura máxima, ela experimenta uma breve rajada de vento que reduz sua velocidade horizontal em 1,50 m/s. Qual a distância que a bola percorre horizontalmente?
Solução
(a) 24,2 m/s
(b) A bola percorre um total de 57,4 m com uma breve rajada de vento.
68. Prove que a trajetória de um projétil é parabólica, tendo a forma\(y=ax+bx^2\). Para obter essa expressão, resolva a equação\(x=v_{0x}t\)\(t\) e substitua-a pela expressão de\(y=v_{0y}t–(1/2)gt^2\) (Essas equações descrevem as\(y\) posições\(x\) e de um projétil que começa na origem.) Você deve obter uma equação da forma\(y=ax+bx^2\) onde\(a\) e\(b\) são constantes.
69. Determine\(R=\frac{v^2_0sin2θ_0}{g}\) o alcance de um projétil em terreno nivelado encontrando o\(t\) momento em que\(y\) se torna zero e substituindo esse valor de\(t\) na expressão por\(x−x_0\), observando que\(R=x−x_0\)
Solução
\(y−y_0=0=v_{0y}t−\frac{1}{2}gt^2=(v_0sinθ)t−\frac{1}{2}gt^2\)
para que\(t=\frac{2(v0sinθ)}{g}\)
\(x−x_0=v_0xt=(v_0cosθ)t=R,\) e substituindo\(t\) dê:
\(R=v_0cosθ(\frac{2v_0sinθ}{g})=\frac{2v^2_0sinθcosθ}{g}\)
desde então\(2sinθcosθ=sin2θ\), o intervalo é:
\(R=\frac{v_0^2sin2θ}{g}\)
70. Resultados irracionais
(a) Encontre o alcance máximo de um super canhão que tenha uma velocidade de focinho de 4,0 km/s.
(b) O que não é razoável na faixa que você encontrou?
(c) A premissa não é razoável ou a equação disponível é inaplicável? Explique sua resposta.
(d) Se tal velocidade de focinho pudesse ser obtida, discuta os efeitos da resistência do ar, da diluição do ar com a altitude e a curvatura da Terra no alcance do super canhão.
71. Construa seu próprio problema
Considere uma bola jogada por cima de uma cerca. Crie um problema no qual você calcule a velocidade inicial necessária da bola para simplesmente limpar a cerca. Entre as coisas a determinar estão; a altura da cerca, a distância até a cerca do ponto de lançamento da bola e a altura em que a bola é liberada. Você também deve considerar se é possível escolher a velocidade inicial da bola e apenas calcular o ângulo em que ela é lançada. Examine também a possibilidade de várias soluções, dadas as distâncias e alturas que você escolheu.
3.5: Adição de velocidades
72. Bryan Allen pedalou uma aeronave movida a energia humana pelo Canal da Mancha, dos penhascos de Dover até Cap Gris-Nez, em 12 de junho de 1979.
(a) Ele voou por 169 min a uma velocidade média de 3,53 m/s na direção\(45º\) sul do leste. Qual foi seu deslocamento total?
(b) Allen encontrou um vento contrário com média de 2,00 m/s quase precisamente na direção oposta de seu movimento em relação à Terra. Qual era sua velocidade média em relação ao ar?
(c) Qual foi seu deslocamento total em relação à massa de ar?
Solução
(a)\(35.8 km, 45º\) sul do leste
(b)\(5.53 m/s, 45º\) sul do leste
(c)\(56.1 km, 45º\) sul do leste
73. Uma gaivota voa a uma velocidade de 9,00 m/s diretamente no vento.
(a) Se a ave levar 20,0 min para viajar 6,00 km em relação à Terra, qual é a velocidade do vento?
(b) Se o pássaro se virar e voar com o vento, quanto tempo ele demorará para retornar 6,00 km?
(c) Discuta como o vento afeta o tempo total de ida e volta em comparação com o que seria sem vento.
74. Perto do final de uma maratona, os dois primeiros corredores são separados por uma distância de 45,0 m. O corredor da frente tem uma velocidade de 3,50 m/s e o segundo uma velocidade de 4,20 m/s.
(a) Qual é a velocidade do segundo corredor em relação ao primeiro?
(b) Se o corredor da frente estiver a 250 m da linha de chegada, quem vencerá a corrida, supondo que corra em velocidade constante?
(c) Qual será a distância à frente da vencedora quando cruzar a linha de chegada?
Solução
(a) 0,70 m/s mais rápida
(b) O segundo corredor vence
(c) 4,17 m
75. Verifique se a moeda lançada pelo passageiro da companhia aérea no Exemplo viaja 144 m horizontalmente enquanto cai 1,50 m no quadro de referência da Terra.
76. Um zagueiro de futebol está se movendo para trás a uma velocidade de 2,00 m/s quando lança um passe para um jogador de 18,0 m direto no campo. A bola é lançada em um ângulo em\(25.0º\) relação ao solo e presa na mesma altura em que é lançada. Qual é a velocidade inicial da bola em relação ao zagueiro?
Solução
\(17.0 m/s, 22.1º\)
77. Um navio parte de Roterdã, Holanda, em direção ao norte a 7,00 m/s em relação à água. A corrente oceânica local é de 1,50 m/s na direção\(40.0º\) norte do leste. Qual é a velocidade da nave em relação à Terra?
78. (a) Um avião a jato voando de Darwin, Austrália, tem uma velocidade de ar de 260 m/s na direção\(5.0º\) sul do oeste. Está na corrente de jato, que está soprando a 35,0 m/s na direção\(15º\) sul do leste. Qual é a velocidade do avião em relação à Terra?
(b) Discuta se suas respostas são consistentes com suas expectativas quanto ao efeito do vento na trajetória do avião.
Solução
(a)\(230 m/s, 8.0º\) sul do oeste
(b) O vento deve fazer com que o avião viaje mais devagar e mais para o sul, que foi calculado.
79. (a) Em que direção a nave em Exercício teria que viajar para ter uma velocidade reta para o norte em relação à Terra, supondo que sua velocidade em relação à água permaneça\(7.00 m/s\)?
(b) Qual seria sua velocidade em relação à Terra?
80. (a) Outro avião está voando em uma corrente de jato que está soprando a 45,0 m/s em uma direção 20º tamanho 12 {"20º"} {} ao sul do leste (como no Exercício). Sua direção de movimento em relação à Terra é 45,0º tamanho 12 {"45,0º"} {} ao sul do oeste, enquanto sua direção de viagem em relação ao ar é 5,00º tamanho 12 {5,00º} {} sul do oeste. Qual é a velocidade do avião em relação à massa de ar? (b) Qual é a velocidade do avião em relação à Terra?
Solução
(a) 63,5 m/s
(b) 29,6 m/s
81. Uma sandália cai do topo de um mastro de 15,0 m de altura em um navio que se move a 1,75 m/s para o sul. Calcule a velocidade da sandália quando ela atinge o convés do navio:
(a) em relação ao navio e
(b) em relação a um observador estacionário em terra.
(c) Discuta como as respostas fornecem um resultado consistente para a posição em que a sandália atinge o convés.
82. A velocidade do vento em relação à água é crucial para os veleiros. Suponha que um veleiro esteja em uma corrente oceânica que tenha uma velocidade de 2,20 m/s na direção\(30.0º\) leste do norte em relação à Terra. Ele encontra um vento que tem uma velocidade de 4,50 m/s na direção\(50.0º\) sul do oeste em relação à Terra. Qual é a velocidade do vento em relação à água?
Solução
\(6.68 m/s, 53.3º\) sul ou oeste
83. O grande astrônomo Edwin Hubble descobriu que todas as galáxias distantes estão se afastando da nossa Via Láctea com velocidades proporcionais às suas distâncias. Parece para um observador na Terra que estamos no centro de um universo em expansão. A figura ilustra isso para cinco galáxias situadas ao longo de uma linha reta, com a Via Láctea no centro. Usando os dados da figura, calcule as velocidades:
(a) em relação à galáxia 2 e
(b) em relação à galáxia 5.
Os resultados significam que observadores de todas as galáxias se verão no centro do universo em expansão e provavelmente estariam cientes das velocidades relativas, concluindo que não é possível localizar o centro de expansão com as informações fornecidas.
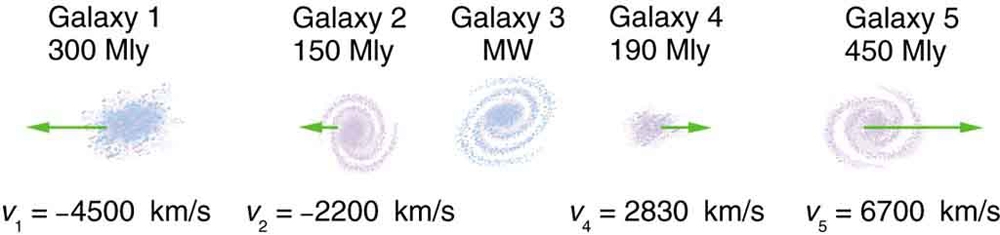
Cinco galáxias em linha reta, mostrando suas distâncias e velocidades em relação à Via Láctea (MW). As distâncias estão em milhões de anos-luz (Mly), onde um ano-luz é a distância que a luz percorre em um ano. As velocidades são quase proporcionais às distâncias. Os tamanhos das galáxias são muito exagerados; uma galáxia média tem cerca de 0,1 Mly de diâmetro.
84. (a) Use os dados de distância e velocidade na Figura para encontrar a taxa de expansão em função da distância.
(b) Se você extrapolar para trás no tempo, há quanto tempo todas as galáxias estariam aproximadamente na mesma posição? As duas partes desse problema dão uma ideia de como a constante do Hubble para expansão universal e o tempo de volta ao Big Bang são determinados, respectivamente.
Solução
(a)\(H_{average}=14.9\frac{km/s}{Mly}\)
(b) 20,2 bilhões de anos
85. Um atleta cruza um rio de 25 m de largura nadando perpendicularmente à corrente da água a uma velocidade de 0,5 m/s em relação à água. Ele alcança o lado oposto a uma distância de 40 m a jusante do seu ponto de partida. Com que rapidez a água do rio está fluindo em relação ao solo? Qual é a velocidade do nadador em relação a um amigo em repouso no chão?
86. Um navio navegando na Corrente do Golfo está indo para o\(25.0º\) oeste do norte a uma velocidade de 4,00 m/s em relação à água. Sua velocidade em relação à Terra está a\(4.80 m/s 5.00º\) oeste do norte. Qual é a velocidade da Corrente do Golfo? (A velocidade obtida é típica da Corrente do Golfo, a algumas centenas de quilômetros da costa leste dos Estados Unidos.)
Solução
\(1.72 m/s, 42.3º\) ao norte do leste
87. Um jogador de hóquei no gelo está se movendo a 8,00 m/s quando acerta o disco em direção ao gol. A velocidade do disco em relação ao jogador é de 29,0 m/s. A linha entre o centro do gol e o jogador faz um\(90.0º\) ângulo em relação ao seu caminho, conforme mostrado na Figura. Qual ângulo a velocidade do disco deve fazer em relação ao jogador (em seu quadro de referência) para atingir o centro do gol?
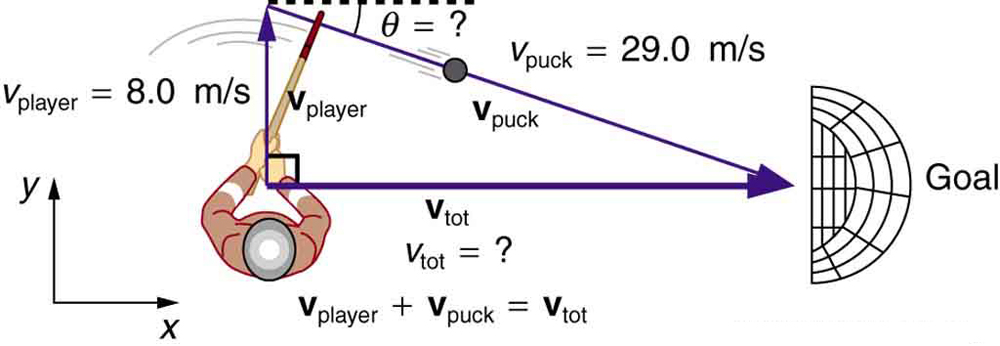
Um jogador de hóquei no gelo que se move pela pista deve atirar para trás para dar ao disco uma velocidade em direção ao gol.
88. Resultados irracionais
Suponha que você deseje enviar suprimentos diretamente para astronautas em uma órbita de 36.000 km acima da superfície da Terra.
(a) Em que velocidade os suprimentos devem ser lançados?
(b) O que não é razoável nessa velocidade?
(c) Há algum problema com a velocidade relativa entre os suprimentos e os astronautas quando os suprimentos atingem sua altura máxima?
(d) A premissa não é razoável ou a equação disponível é inaplicável? Explique sua resposta.
89. Resultados irracionais
Um avião comercial tem uma velocidade aérea do\(280 m/s\) leste e voa com um forte vento de cauda. Ele viaja 3000 km em uma direção\(5º\) ao sul do leste em 1,50 h.
(a) Qual era a velocidade do avião em relação ao solo?
(b) Calcule a magnitude e a direção da velocidade do vento de cauda.
(c) O que não é razoável nessas duas velocidades?
(d) Qual premissa não é razoável?
90. Construa seu próprio problema
Considere um avião indo para uma pista em um vento cruzado. Crie um problema no qual você calcule o ângulo que o avião deve voar em relação à massa de ar para ter uma velocidade paralela à pista. Entre as coisas a considerar estão a direção da pista, a velocidade e direção do vento (sua velocidade) e a velocidade do avião em relação à massa de ar. Calcule também a velocidade do avião em relação ao solo. Discuta quaisquer manobras de última hora que o piloto precise realizar para que o avião pouse com as rodas apontando diretamente para a pista.


