3.4: Movimento do projétil
- Page ID
- 194358
Objetivos de
Ao final desta seção, você poderá:
- Identifique e explique as propriedades de um projétil, como aceleração devido à gravidade, alcance, altura máxima e trajetória.
- Determine a localização e a velocidade de um projétil em diferentes pontos de sua trajetória.
- Aplique o princípio da independência de movimento para resolver problemas de movimento de projéteis.
O movimento do projétil é o movimento de um objeto lançado ou projetado no ar, sujeito apenas à aceleração da gravidade. O objeto é chamado de projétil e seu caminho é chamado de trajetória. O movimento dos objetos que caem, conforme abordado em Fundamentos da Solução de Problemas para Cinemática Unidimensional, é um tipo simples de movimento unidimensional de projétil no qual não há movimento horizontal. Nesta seção, consideramos o movimento bidimensional do projétil, como o de uma bola de futebol ou outro objeto para o qual a resistência do ar é insignificante.
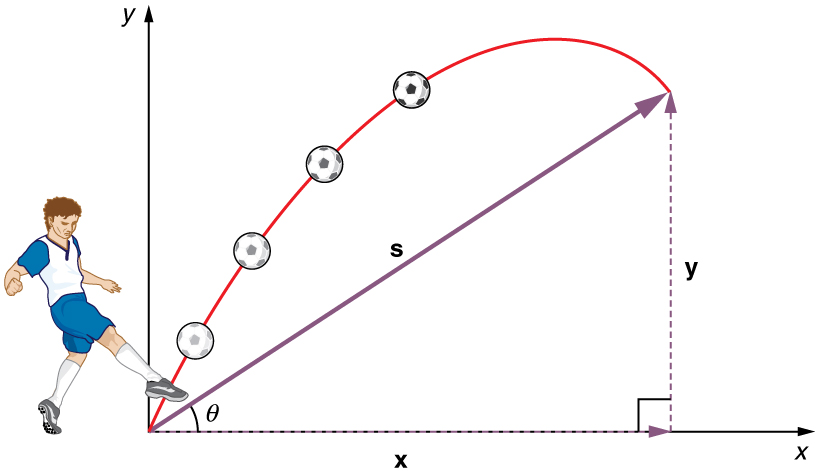
O fato mais importante a lembrar aqui é que os movimentos ao longo dos eixos perpendiculares são independentes e, portanto, podem ser analisados separadamente. Esse fato foi discutido em Cinemática em Duas Dimensões: Uma Introdução, onde os movimentos verticais e horizontais eram vistos como independentes. A chave para analisar o movimento bidimensional do projétil é dividi-lo em dois movimentos, um ao longo do eixo horizontal e outro ao longo da vertical. (Essa escolha de eixos é a mais sensata, porque a aceleração devido à gravidade é vertical — portanto, não haverá aceleração ao longo do eixo horizontal quando a resistência do ar for insignificante.) Como é habitual, chamamos o eixo horizontal de eixo x e o eixo vertical de eixo y. A figura ilustra a notação para deslocamento, onde\(\displaystyle s\) é definido como sendo o deslocamento total\(\displaystyle x\) e\(\displaystyle y\) são seus componentes ao longo dos eixos horizontal e vertical, respectivamente. As magnitudes desses vetores são s, x e y. (Note que na última seção usamos a notação\(\displaystyle A\) para representar um vetor com componentes\(\displaystyle A_x\)\(\displaystyle A_y\) e. Se continuássemos com esse formato, chamaríamos deslocamento\(\displaystyle s\) com componentes\(\displaystyle s_x\)\(\displaystyle s_y\) e. No entanto, para simplificar a notação, simplesmente representaremos os vetores componentes como\(\displaystyle x\)\(\displaystyle y\) e.)
Obviamente, para descrever o movimento, devemos lidar com a velocidade e a aceleração, bem como com o deslocamento. Também devemos encontrar seus componentes ao longo dos eixos x e y. Assumiremos que todas as forças, exceto a gravidade (como resistência do ar e atrito, por exemplo) são insignificantes. Os componentes da aceleração são então muito simples:\(\displaystyle a_y=–g=–9.80 m/s^2\) (. (Observe que essa definição pressupõe que a direção ascendente é definida como a direção positiva. Se você organizar o sistema de coordenadas de forma que a direção descendente seja positiva, a aceleração devida à gravidade terá um valor positivo.) Porque a gravidade é vertical,\(\displaystyle a_x=0\). Ambas as acelerações são constantes, então as equações cinemáticas podem ser usadas.
REVISÃO DE EQUAÇÕES CINEMÁTICAS (CONSTANTE)
\(\displaystyle x=x_0+\bar{v}t\)
\(\displaystyle \bar{v}=\frac{v_0+v}{2}\)
\(\displaystyle v=v_0+at\)
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle v^2=v^2_0+2a(x−x_0)\).
Dadas essas suposições, as seguintes etapas são então usadas para analisar o movimento do projétil:
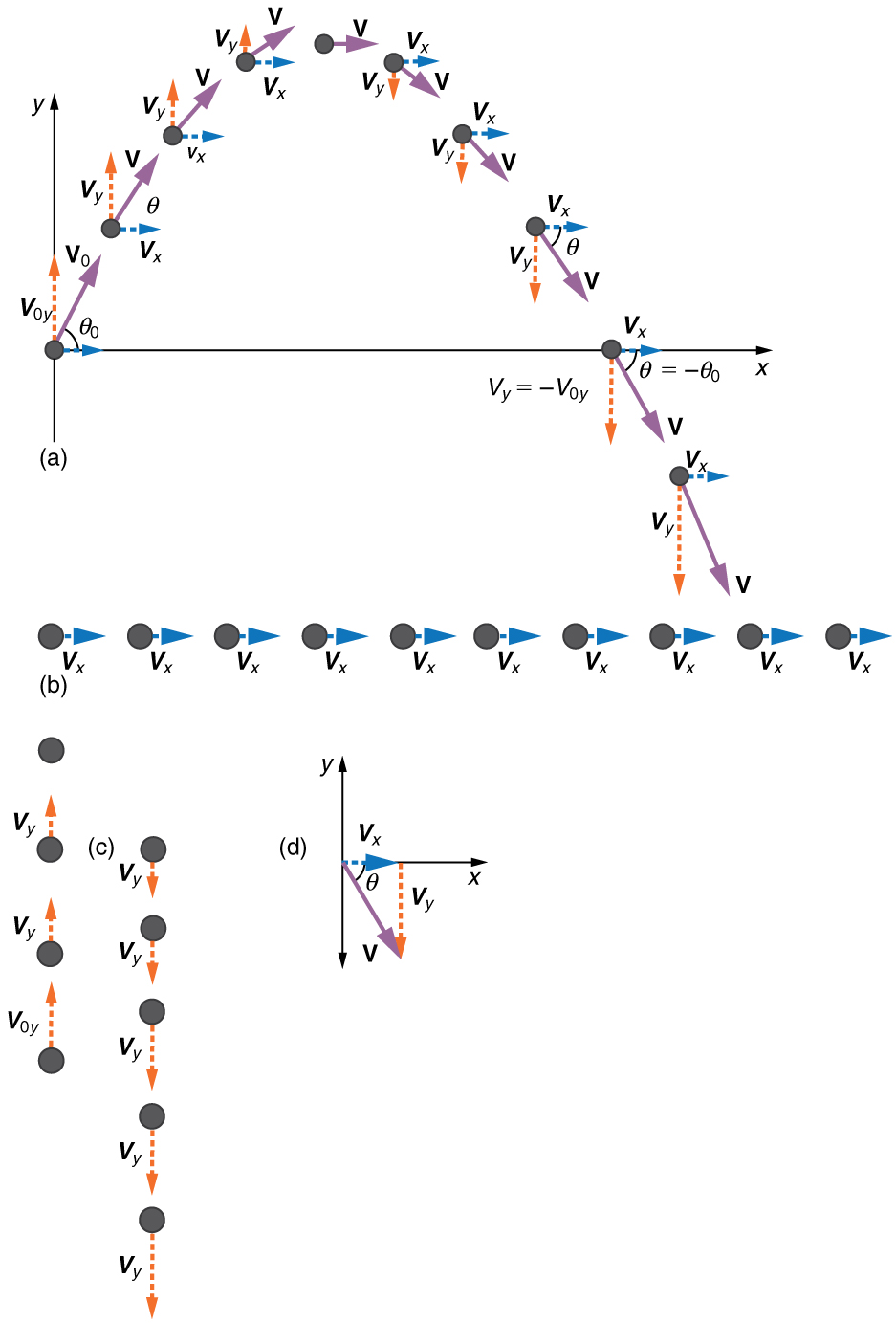
Etapa 1. Resolva ou divida o movimento em componentes horizontais e verticais ao longo dos eixos x e y. Esses eixos são perpendiculares, então\(\displaystyle A_x=Acosθ\) e\(\displaystyle A_y=Asinθ\) são usados. A magnitude dos componentes do deslocamento\(\displaystyle s\) ao longo desses eixos é\(\displaystyle x\)\(\displaystyle y\) e. As magnitudes dos componentes da velocidade\(\displaystyle v\) são\(\displaystyle v_x=vcosθ\) e\(\displaystyle v_y=vsinθ\), onde\(\displaystyle v\) é a magnitude da velocidade e θ é sua direção, conforme mostrado na Figura. Os valores iniciais são indicados com um subscrito 0, como de costume.
Etapa 2. Trate o movimento como dois movimentos unidimensionais independentes, um horizontal e outro vertical. As equações cinemáticas para movimento horizontal e vertical assumem as seguintes formas:
\(\displaystyle \text{Horizontal Motion}(a_x=0)\)
\(\displaystyle x=x_0+v_xt\)
\(\displaystyle v_x=v_{0x}=v_x=\text{velocity is a constant}\).
\(\displaystyle \text{Vertical Motion(assuming positive is up}a_y=−g=−9.80m/s^2)\)
\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\)
\(\displaystyle v_y=v_{0y}−gt\)
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\)
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
Etapa 3. Resolva as incógnitas em dois movimentos separados: um horizontal e outro vertical. Observe que a única variável comum entre os movimentos é o tempo t. Os procedimentos de resolução de problemas aqui são os mesmos da cinemática unidimensional e são ilustrados nos exemplos resolvidos abaixo.
Etapa 4. Recombine os dois movimentos para encontrar o deslocamento total\(\displaystyle s\) e a velocidade\(\displaystyle v\). Como os movimentos x e y são perpendiculares, determinamos esses vetores usando as técnicas descritas em Adição e Subtração de Vetores: Métodos Analíticos\(\displaystyle A=\sqrt{A^2_x+A^2_y}\) e empregando e\(\displaystyle θ=tan^{−1}(A_y/A_x)\) na seguinte forma, onde\(\displaystyle θ\) está a direção do deslocamento\(\displaystyle s\) e\(\displaystyle θ_v\) é a direção da velocidade\(\displaystyle v\):
Deslocamento e velocidade totais
\(\displaystyle s=\sqrt{x^2+y^2}\)
\(\displaystyle θ=tan^{−1}(y/x)\)
\(\displaystyle v=\sqrt{v^2_x+v^2_y}\)
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\).
Exemplo\(\displaystyle \PageIndex{1}\): A Fireworks Projectile Explodes High and Away
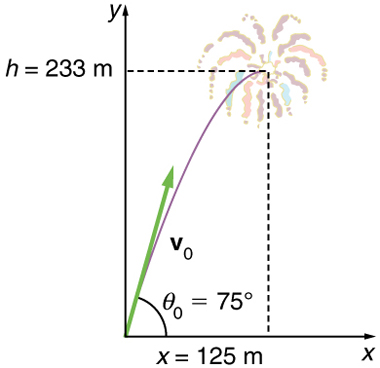
Durante uma exibição de fogos de artifício, um projétil é lançado no ar com uma velocidade inicial de 70,0 m/s em um ângulo de 75,0º acima da horizontal, conforme ilustrado na Figura. O fusível é programado para acender a concha assim que ela atinge seu ponto mais alto acima do solo.
- Calcule a altura em que a concha explode.
- Quanto tempo passou entre o lançamento do projétil e a explosão?
- Qual é o deslocamento horizontal da concha quando ela explode?
Estratégia
Como a resistência do ar é insignificante para o invólucro não detonado, o método de análise descrito acima pode ser usado. O movimento pode ser dividido em movimentos horizontais e verticais nos quais\(\displaystyle a_x=0\)\(\displaystyle a_y=–g\) e. Podemos então definir\(\displaystyle x_0\) e\(\displaystyle y_0\) ser zero e resolver as quantidades desejadas.
Solução para (a)
Por “altura”, queremos dizer a altitude ou posição vertical y acima do ponto de partida. O ponto mais alto em qualquer trajetória, chamado ápice, é atingido quando\(\displaystyle v_y=0\). Como conhecemos as velocidades inicial e final, bem como a posição inicial, usamos a seguinte equação para encontrar\(\displaystyle y\):
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
Como\(\displaystyle y_0\) ambos\(\displaystyle v_y\) são zero, a equação simplifica para
\(\displaystyle 0=v^2_{0y}−2gy.\)
Resolvendo\(\displaystyle y\) doações
\(\displaystyle y=\frac{v^2_{0y}}{2g}\).
Agora devemos encontrar\(\displaystyle v_{0y}\) a componente da velocidade inicial na direção y. É dado por\(\displaystyle v_{0y}=v_0sinθ\), onde\(\displaystyle v_{0y}\) é a velocidade inicial de 70,0 m/s e\(\displaystyle θ_0=75.0º\) é o ângulo inicial. Assim,
\(\displaystyle v_{0y}=v_0sinθ_0=(70.0 m/s)(sin 75º)=67.6 m/s.\)
e\(\displaystyle y\) é
\(\displaystyle y=\frac{(67.6 m/s)^2}{2(9.80 m/s^2)}\),
para que
\(\displaystyle y=233m.\)
Discussão para (a)
Observe que, como o aumento é positivo, a velocidade inicial é positiva, assim como a altura máxima, mas a aceleração devido à gravidade é negativa. Observe também que a altura máxima depende apenas do componente vertical da velocidade inicial, de modo que qualquer projétil com um componente vertical inicial de velocidade de 67,6 m/s alcançará uma altura máxima de 233 m (negligenciando a resistência do ar). Os números neste exemplo são razoáveis para grandes fogos de artifício, cujos projéteis atingem essas alturas antes de explodirem. Na prática, a resistência do ar não é completamente desprezível e, portanto, a velocidade inicial teria que ser um pouco maior do que a fornecida para atingir a mesma altura.
Solução para (b)
Como em muitos problemas de física, há mais de uma maneira de resolver por enquanto até o ponto mais alto. Nesse caso, o método mais fácil é usar\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\). Como y0 é zero, essa equação se reduz a simplesmente
\(\displaystyle y=\frac{1}{2}(v_{0y}+v_y)t\).
Observe que a velocidade vertical final,\(\displaystyle v_y\), no ponto mais alto é zero. Assim,
\(\displaystyle t=\frac{2y}{(v_{0y}+v_y)}=\frac{2(233 m)}{(67.6 m/s)}=6.90 s.\)
Discussão para (b)
Esse tempo também é razoável para grandes fogos de artifício. Quando você puder ver o lançamento de fogos de artifício, notará que alguns segundos se passam antes que o projétil exploda. (Outra forma de encontrar o tempo é usando\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\) e resolvendo a equação quadrática para\(\displaystyle t\).)
Solução para (c)
Porque a resistência do ar é insignificante\(\displaystyle a_x=0\) e a velocidade horizontal é constante, conforme discutido acima. O deslocamento horizontal é a velocidade horizontal multiplicada pelo tempo, conforme dado por\(\displaystyle x=x_0+v_xt\), onde\(\displaystyle x_0\) é igual a zero:
\(\displaystyle x=v_xt,\)
onde\(\displaystyle v_x\) é o componente x da velocidade, que é dado por\(\displaystyle v_x=v_0cosθ_0\). Agora,
\(\displaystyle v_x=v_0cosθ_0=(70.0 m/s)(cos 75.0º)=18.1 m/s.\)
O tempo\(\displaystyle t\) para os dois movimentos é o mesmo, e assim\(\displaystyle x\) é
\(\displaystyle x=(18.1 m/s)(6.90 s)=125 m.\)
Discussão para (c)
O movimento horizontal é uma velocidade constante na ausência de resistência do ar. O deslocamento horizontal encontrado aqui pode ser útil para evitar que os fragmentos de fogos de artifício caiam sobre os espectadores. Quando o projétil explode, a resistência do ar tem um efeito importante e muitos fragmentos cairão diretamente abaixo.
Ao resolver a parte (a) do exemplo anterior, a expressão que encontramos para y é válida para qualquer movimento de projétil em que a resistência do ar seja insignificante. Chame a altura máxima\(\displaystyle y=h\); então,
\(\displaystyle h=\frac{v^2_{0y}}{2g}\).
Essa equação define a altura máxima de um projétil e depende somente do componente vertical da velocidade inicial.
DEFININDO UM SISTEMA DE COORDENADAS
É importante configurar um sistema de coordenadas ao analisar o movimento do projétil. Uma parte da definição do sistema de coordenadas é definir uma origem para as\(\displaystyle y\) posições\(\displaystyle x\) e. Freqüentemente, é conveniente escolher a posição inicial do objeto como origem, de forma que\(\displaystyle x_0=0\)\(\displaystyle y_0=0\) e. Também é importante definir as direções positivas e negativas nas\(\displaystyle x\)\(\displaystyle y\) direções e. Normalmente, definimos a direção vertical positiva como ascendente, e a direção horizontal positiva geralmente é a direção do movimento do objeto. Nesse caso, a aceleração vertical,\(\displaystyle g\), assume um valor negativo (já que é direcionada para baixo em direção à Terra). No entanto, às vezes é útil definir as coordenadas de forma diferente. Por exemplo, se você estiver analisando o movimento de uma bola lançada para baixo do topo de um penhasco, pode fazer sentido definir a direção positiva para baixo, já que o movimento da bola é somente na direção descendente. Se for esse o caso, g assume um valor positivo.
Exemplo\(\displaystyle \PageIndex{2}\): Calculating Projectile Motion: Hot Rock Projectile
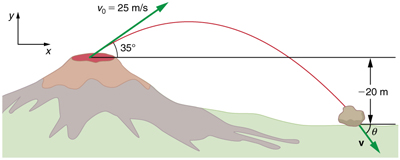
O Kilauea, no Havaí, é o vulcão mais ativo do mundo. Vulcões muito ativos ejetam caracteristicamente rochas e lava em brasa, em vez de fumaça e cinzas. Suponha que uma rocha grande seja ejetada do vulcão com uma velocidade de 25,0 m/s e em um ângulo acima da horizontal, conforme mostrado na Figura. A rocha atinge a lateral do vulcão a uma altitude 20,0 m abaixo do ponto de partida. (a) Calcule o tempo que a rocha leva para seguir esse caminho. (b) Quais são a magnitude e a direção da velocidade da rocha no impacto?
Estratégia
Novamente, resolver esse movimento bidimensional em dois movimentos unidimensionais independentes nos permitirá resolver as quantidades desejadas. O tempo em que um projétil está no ar é governado apenas por seu movimento vertical. Vamos resolver pela\(\displaystyle t\) primeira vez. Enquanto a rocha sobe e desce verticalmente, o movimento horizontal continua a uma velocidade constante. Este exemplo pede a velocidade final. Assim, os resultados verticais e horizontais serão recombinados para obter\(\displaystyle v\) e,\(\displaystyle θ_v\) no momento final, t determinado na primeira parte do exemplo.
Solução para (a)
Enquanto a rocha está no ar, ela sobe e depois desce para uma posição final 20,0 m abaixo de sua altitude inicial. Podemos encontrar tempo para isso usando
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\).
Se considerarmos que\(\displaystyle y_0\) a posição inicial é zero, então a posição final é\(\displaystyle y=−20.0 m\). Agora, a velocidade vertical inicial é o componente vertical da velocidade inicial, encontrado em\(\displaystyle v_{0y}=v_0sinθ_0 = (25.0 m/s)(sin 35.0º) = 14.3 m/s.\) Substituindo valores conhecidos produz
\(\displaystyle −20.0 m=(14.3 m/s)t−(4.90 m/s^2)t^2\).
A reorganização dos termos fornece uma equação quadrática em\(\displaystyle t\):
\(\displaystyle (4.90 m/s^2)t^2−(14.3 m/s)t−(20.0 m)=0.\)
Essa expressão é uma equação quadrática da forma\(\displaystyle at^2+bt+c=0\), onde estão as constantes\(\displaystyle a=4.90, b=–14.3\), e\(\displaystyle c=–20.0.\) Suas soluções são dadas pela fórmula quadrática:
\(\displaystyle t=\frac{−b±\sqrt{b^2−4ac}}{2a}\).
Essa equação produz duas soluções:\(\displaystyle t=3.96\)\(\displaystyle t=–1.03\) e. (É deixado como um exercício para o leitor verificar essas soluções.) A hora é\(\displaystyle t=3.96s\) ou\(\displaystyle –1.03s\). O valor negativo do tempo implica um evento antes do início do movimento e, portanto, o descartamos. Assim,
\(\displaystyle t=3.96 s.\)
Discussão para (a)
O tempo de movimento do projétil é completamente determinado pelo movimento vertical. Portanto, qualquer projétil que tenha uma velocidade vertical inicial de 14,3 m/s e caia 20,0 m abaixo de sua altitude inicial passará 3,96 s no ar.
Solução para (b)
A partir das informações agora em mãos, podemos encontrar as velocidades finais horizontais e verticais\(\displaystyle v_x\)\(\displaystyle v_y\) e combiná-las para encontrar a velocidade total v e o ângulo\(\displaystyle θ_0\) que ela faz com a horizontal. Obviamente,\(\displaystyle v_x\) é constante para que possamos resolvê-lo em qualquer local horizontal. Nesse caso, escolhemos o ponto de partida, pois conhecemos a velocidade inicial e o ângulo inicial. Portanto:
\(\displaystyle v_x=v_0cosθ_0=(25.0 m/s)(cos 35º)=20.5 m/s.\)
A velocidade vertical final é dada pela seguinte equação:
\(\displaystyle v_y=v_{0y}−gt\),
onde\(\displaystyle v_{0y}\) foi encontrado na parte (a) 14,3 m/s. Assim,
\(\displaystyle v_y=14.3 m/s−(9.80 m/s^2)(3.96 s)\)
para que
\(\displaystyle v_y=−24.5 m/s.\)
Para encontrar a magnitude da velocidade final v, combinamos seus componentes perpendiculares, usando a seguinte equação:
\(\displaystyle v=\sqrt{v^2_x+v^2_y}=\sqrt{(20.5 m/s)^2+(−24.5 m/s)^2}\),
que dá
\(\displaystyle v=31.9 m/s.\)
A direção θv é encontrada na equação:
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\)
para que
\(\displaystyle θ_v=tan^{−1}(−24.5/20.5)=tan^{−1}(−1.19).\)
Assim,
\(\displaystyle θ_v=−50.1º.\)
Discussão para (b)
O ângulo negativo significa que a velocidade está 50,1º abaixo da horizontal. Esse resultado é consistente com o fato de que a velocidade vertical final é negativa e, portanto, descendente — como seria de esperar, porque a altitude final é 20,0 m abaixo da altitude inicial. (Veja a Figura.)
Uma das coisas mais importantes ilustradas pelo movimento do projétil é que os movimentos verticais e horizontais são independentes um do outro. Galileu foi a primeira pessoa a compreender totalmente essa característica. Ele o usou para prever o alcance de um projétil. Em terreno nivelado, definimos alcance como sendo a distância horizontal percorrida por um projétil. Galileu e muitos outros estavam interessados na variedade de projéteis principalmente para fins militares, como canhões de mira. No entanto, investigar o alcance dos projéteis pode lançar luz sobre outros fenômenos interessantes, como as órbitas dos satélites ao redor da Terra. Vamos considerar ainda mais o alcance do projétil.
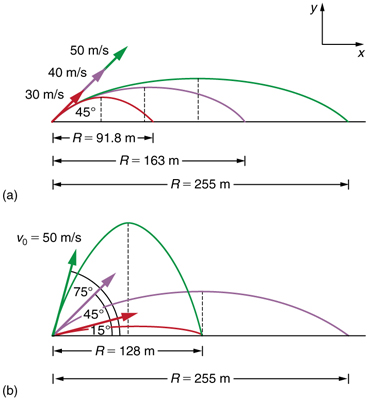
Como a velocidade inicial de um projétil afeta seu alcance? Obviamente, quanto maior a velocidade inicial\(\displaystyle v_0\), maior o alcance, conforme mostrado na Figura (a). O ângulo inicial\(\displaystyle θ_0\) também tem um efeito dramático na faixa, conforme ilustrado na Figura (b). Para uma velocidade inicial fixa, como a que pode ser produzida por um canhão, o alcance máximo é obtido com\(\displaystyle θ_0=45º\). Isso é verdade apenas para condições que negligenciam a resistência do ar. Se a resistência do ar for considerada, o ângulo máximo é de aproximadamente\(\displaystyle 38º\). Curiosamente, para cada ângulo inicial\(\displaystyle 45º\), exceto, há dois ângulos que fornecem o mesmo alcance — a soma desses ângulos é\(\displaystyle 90º\). O alcance também depende do valor da aceleração da gravidade\(\displaystyle g\). O astronauta lunar Alan Shepherd conseguiu dirigir uma bola de golfe a uma grande distância na Lua porque a gravidade é mais fraca lá. O alcance\(\displaystyle R\) de um projétil em terreno plano para o qual a resistência do ar é insignificante é dado por
\(\displaystyle R=\frac{v^2_0sin2θ_0}{g}\),
onde\(\displaystyle v_0\) é a velocidade inicial e\(\displaystyle θ_0\) é o ângulo inicial em relação à horizontal. A prova dessa equação é deixada como um problema de fim de capítulo (dicas são dadas), mas ela se encaixa nas principais características do alcance do projétil, conforme descrito.
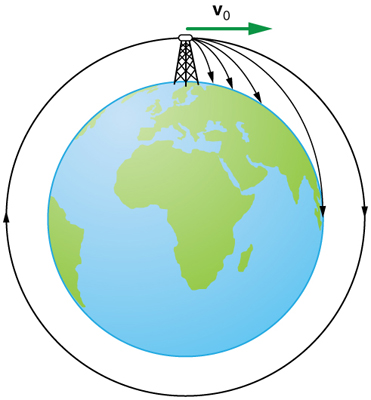
Quando falamos do alcance de um projétil em terreno plano, assumimos que\(\displaystyle R\) é muito pequeno em comparação com a circunferência da Terra. Se, no entanto, o alcance for grande, a Terra se curva abaixo do projétil e a aceleração da gravidade muda de direção ao longo do caminho. O alcance é maior do que o previsto pela equação de alcance dada acima porque o projétil tem mais a cair do que em terreno nivelado. (Veja a Figura.) Se a velocidade inicial for grande o suficiente, o projétil entra em órbita. Isso é chamado de velocidade de saída. Essa possibilidade foi reconhecida séculos antes de ser realizada. Quando um objeto está em órbita, a Terra se curva para longe de baixo do objeto na mesma velocidade em que ele cai. Assim, o objeto cai continuamente, mas nunca atinge a superfície. Esses e outros aspectos do movimento orbital, como a rotação da Terra, serão abordados analiticamente e com maior profundidade posteriormente neste texto.
Mais uma vez, vemos que pensar em um tópico, como o alcance de um projétil, pode nos levar a outros, como as órbitas da Terra. Além das velocidades, examinaremos a adição de velocidades, que é outro aspecto importante da cinemática bidimensional e também fornecerá informações além do tópico imediato.
EXPLORAÇÕES DE PHET: MOVIMENTO DE PROJÉTEIS
Tire um Buick de um canhão! Aprenda sobre o movimento do projétil disparando vários objetos. Defina o ângulo, a velocidade inicial e a massa. Adicione resistência ao ar. Faça desta simulação um jogo tentando acertar um alvo.

Resumo
- O movimento do projétil é o movimento de um objeto no ar que está sujeito apenas à aceleração da gravidade.
- Para resolver problemas de movimento do projétil, execute as seguintes etapas:
- Determine um sistema de coordenadas. Em seguida, resolva a posição e/ou a velocidade do objeto nos componentes horizontal e vertical. Os componentes da posição s são dados pelas quantidades x e y, e os componentes da velocidade v são dados por vx=vcosθ e vy=vsinθ, onde v é a magnitude da velocidade e θ é sua direção.
2. Analise o movimento do projétil na direção horizontal usando as seguintes equações:
\(\displaystyle \text{Horizontal motion}(a_x=0)\)
\(\displaystyle x=x_0+v_xt\)
\(\displaystyle v_x=v_{0x}=v_x=\text{velocity is a constant}\).
3. Analise o movimento do projétil na direção vertical usando as seguintes equações:
\(\displaystyle \text{Vertical motion(Assuming positive direction is up;}a_y=−g=−9.80 m/s^2)\)
\(\displaystyle y=y_0+\frac{1}{2}(v_{0y}+v_y)t\)
\(\displaystyle v_y=v_{0y}−gt\)
\(\displaystyle y=y_0+v_{0y}t−\frac{1}{2}gt^2\)
\(\displaystyle v^2_y=v^2_{0y}−2g(y−y_0)\).
4. Recombine os componentes horizontal e vertical de localização e/ou velocidade usando as seguintes equações:
\(\displaystyle s=\sqrt{x^2+y^2}\)
\(\displaystyle θ=tan^{−1}(y/x)\)
\(\displaystyle v=\sqrt{v^2_x+v^2_y}\)
\(\displaystyle θ_v=tan^{−1}(v_y/v_x)\).
- A altura máxima\(\displaystyle h\) de um projétil lançado com velocidade vertical inicial\(\displaystyle v_{0y}\) é dada por
\(\displaystyle h=\frac{v^2_{0y}}{2g}\).
- A distância horizontal máxima percorrida por um projétil é chamada de alcance. O alcance\(\displaystyle R\) de um projétil em terreno plano lançado em um ângulo\(\displaystyle θ_0\) acima da horizontal com a velocidade inicial\(\displaystyle v_0\) é dado por
\(\displaystyle R=\frac{v^2_0sin2θ_0}{g}\).
Glossário
- resistência ao ar
- uma força de atrito que retarda o movimento dos objetos à medida que eles viajam pelo ar; ao resolver problemas básicos de física, a resistência do ar é considerada zero
- cinemática
- o estudo do movimento sem levar em conta a massa ou a força
- moção
- deslocamento de um objeto em função do tempo
- projétil
- um objeto que viaja pelo ar e experimenta apenas aceleração devido à gravidade
- movimento do projétil
- o movimento de um objeto que está sujeito apenas à aceleração da gravidade
- alcance
- a distância horizontal máxima que um projétil percorre
- trajetória
- o caminho de um projétil pelo ar


