Skip to main content
Global

3.3: Adição e subtração de vetores - métodos analíticos

  1. Last updated
  2. Save as PDF
  • Page ID
    194374

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Entenda as regras de adição e subtração de vetores usando métodos analíticos.
    • Aplique métodos analíticos para determinar vetores de componentes verticais e horizontais.
    • Aplique métodos analíticos para determinar a magnitude e a direção de um vetor resultante.

    Os métodos analíticos de adição e subtração vetorial empregam geometria e trigonometria simples em vez da régua e do transferidor de métodos gráficos. Parte da técnica gráfica é mantida, porque os vetores ainda são representados por setas para facilitar a visualização. No entanto, os métodos analíticos são mais concisos, precisos e precisos do que os métodos gráficos, que são limitados pela precisão com a qual um desenho pode ser feito. Os métodos analíticos são limitados apenas pela exatidão e precisão com que as quantidades físicas são conhecidas.

    Resolvendo um vetor em componentes perpendiculares

    Técnicas analíticas e triângulos retos andam de mãos dadas na física porque (entre outras coisas) os movimentos ao longo das direções perpendiculares são independentes. Muitas vezes precisamos separar um vetor em componentes perpendiculares. Por exemplo, dado um vetor como\(\displaystyle A\) na Figura, podemos querer descobrir quais são os dois vetores perpendiculares\(\displaystyle A_x\) e\(\displaystyle A_y\) adicionar para produzi-lo.

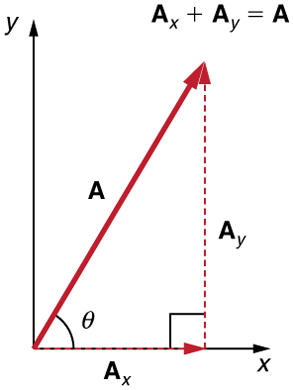
    Na figura dada, um vetor pontilhado A sub x é desenhado a partir da origem ao longo do eixo x. Da cabeça do vetor A sub x outro vetor A sub y é desenhado na direção ascendente. Seu vetor resultante A é desenhado da cauda do vetor A sub x até a cabeça do vetor A sub y em um ângulo teta do eixo x. No gráfico, é mostrado um vetor A, inclinado em um ângulo teta com eixo x. Portanto, o vetor A é a soma dos vetores A sub x e A sub y.
    Figura: O\(\PageIndex{1}\) vetor,\(\displaystyle A\) com sua cauda na origem de um sistema de coordenadas x, y, é mostrado junto com seus componentes x e y,\(\displaystyle A_x\) e.\(\displaystyle A_y\) Esses vetores formam um triângulo reto. As relações analíticas entre esses vetores estão resumidas abaixo.

    \(\displaystyle A_x\)e\(\displaystyle A_y\) são definidos para serem os componentes dos\(\displaystyle A\) eixos x e y. Os três vetores\(\displaystyle A, A_x\) e\(\displaystyle A_y\) formam um triângulo reto:

    \(\displaystyle A_x + A_y = A.\)

    Observe que essa relação entre os componentes do vetor e o vetor resultante é válida apenas para quantidades vetoriais (que incluem magnitude e direção). A relação não se aplica apenas às magnitudes. Por exemplo, se\(\displaystyle A_x=3 m\) leste,\(\displaystyle A_y=4 m\) norte e\(\displaystyle A=5 m \) nordeste, então é verdade que os vetores\(\displaystyle A_x + A_y = A\). No entanto, não é verdade que a soma das magnitudes dos vetores também seja igual. Ou seja,

    \(\displaystyle 3 m+4 m ≠ 5 m\)

    Assim,

    \(\displaystyle A_x+A_y≠A\)

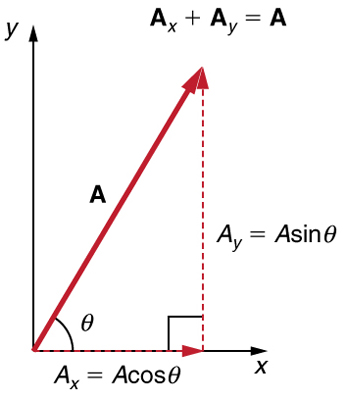
    Se o vetor\(\displaystyle A\) for conhecido, então sua magnitude\(\displaystyle A\) (seu comprimento) e seu ângulo\(\displaystyle θ\) (sua direção) são conhecidos. Para encontrar\(\displaystyle A_x\) e\(\displaystyle A_y\), seus componentes x e y, usamos os seguintes relacionamentos para um triângulo reto.

    \(\displaystyle A_x=Acosθ\)

    e

    \(\displaystyle A_y=Asinθ.\)

    Um vetor pontilhado A sub x cuja magnitude é igual a A cosseno teta é extraído da origem ao longo do eixo x. Da cabeça do vetor A sub x outro vetor A sub y cuja magnitude é igual a A seno teta é desenhado na direção ascendente. Seu vetor resultante A é desenhado da cauda do vetor A sub x até a cabeça do vetor A-y em um ângulo teta do eixo x. Portanto, o vetor A é a soma dos vetores A sub x e A sub y.
    Figura\(\PageIndex{2}\): As magnitudes dos componentes vetoriais\(\displaystyle A_x\) and \(\displaystyle A_y\) can be related to the resultant vector \(\displaystyle A\) and the angle \(\displaystyle θ\) with trigonometric identities. Here we see that \(\displaystyle A_x=Acosθ\) and \(\displaystyle A_y=Asinθ.\)

    Suponha, por exemplo, que A seja o vetor que representa o deslocamento total da pessoa andando em uma cidade considerada em Cinemática em duas dimensões: uma introdução e adição e subtração de vetores: métodos gráficos.

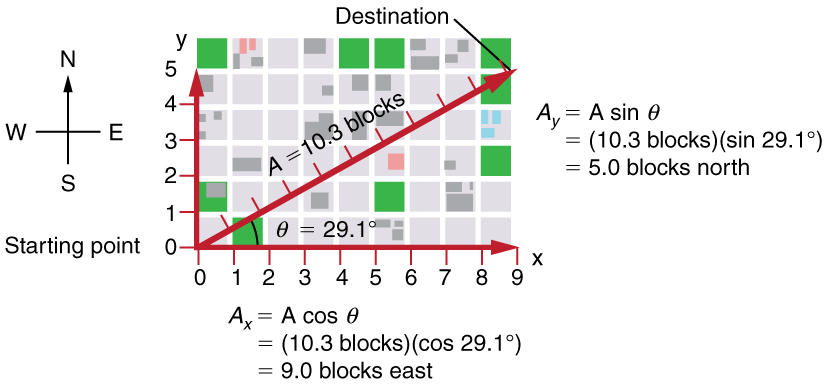
    Na figura dada, um vetor A de magnitude dez pontos três blocos está inclinado em um ângulo de vinte e nove pontos e um graus em relação ao eixo x positivo. O componente horizontal A sub x do vetor A é igual a A cosseno teta, que é igual a dez pontos três blocos multiplicados por cosseno vinte e nove pontos um graus, o que é igual a nove blocos a leste. Além disso, o componente vertical Um sub y do vetor A é igual a A sin teta é igual a dez pontos três blocos multiplicados por seno vinte e nove pontos um graus, o que é igual a cinco pontos zero blocos ao norte.
    Figura\(\PageIndex{3}\): Podemos usar as relações\(\displaystyle A_x=Acosθ\) e determinar\(\displaystyle A_y=Asinθ\) a magnitude dos vetores de componentes horizontais e verticais neste exemplo.

    Em seguida,\(\displaystyle A=10.3\) bloqueia e\(\displaystyle θ=29.1º\), para que

    \(\displaystyle A_x=A\cos θ=(10.3 blocks)(\cos 29.1º)=9.0\)bloqueia

    \(\displaystyle A_y=A\sin θ=(10.3 blocks)(\sin 29.1º)=5.0\)bloqueia.

    Calculando um vetor resultante

    Se os componentes perpendiculares\(\displaystyle A_x\) e\(\displaystyle A_y\) de um vetor\(\displaystyle A\) forem conhecidos, A também poderá ser encontrado analiticamente. Para encontrar a magnitude\(\displaystyle A\) e a direção\(\displaystyle θ\) de um vetor a partir de seus componentes\(\displaystyle A_x\) perpendiculares\(\displaystyle A_y\), usamos as seguintes relações:

    \(\displaystyle A=\sqrt{A_{x^2}+A_{y^2}}\)

    \(\displaystyle θ=tan^{−1}(A_y/A_x)\).

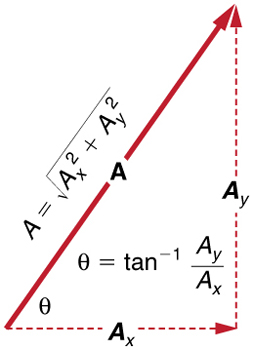
    O vetor A é mostrado com seus componentes horizontais e verticais A sub x e A sub y, respectivamente. A magnitude do vetor A é igual à raiz quadrada de A sub x ao quadrado mais A sub y ao quadrado. O ângulo teta do vetor A com o eixo x é igual à tangente inversa de A sub y sobre A sub x
    Figura\(\PageIndex{4}\): A magnitude e a direção do vetor resultante podem ser determinadas uma vez que os componentes horizontal e vertical\(\displaystyle A_x\) and \(\displaystyle A_y\) have been determined.

    Observe que a equação\(\displaystyle A=\sqrt{A^2_x+A^2_y}\) is just the Pythagorean theorem relating the legs of a right triangle to the length of the hypotenuse. For example, if \(\displaystyle A_x\) and \(\displaystyle A_y\) are 9 and 5 blocks, respectively, then \(\displaystyle A=\sqrt{9^2+5^2}=10.3\) blocks, again consistent with the example of the person walking in a city. Finally, the direction is \(\displaystyle θ=tan^{–1}(5/9)=29.1º\), as before.

    DETERMINANDO VETORES E COMPONENTES VETORIAIS COM MÉTODOS ANALÍTICOS

    Equações\(\displaystyle A_x=Acosθ\) e\(\displaystyle A_y=Asinθ\) são usadas para encontrar os componentes perpendiculares de um vetor, ou seja, ir de\(\displaystyle A\)\(\displaystyle A_x\) e\(\displaystyle θ\) para\(\displaystyle A_y\) e. Equações\(\displaystyle A=\sqrt{A^2_x+A^2_y}\) e\(\displaystyle θ=tan^{–1}(A_y/A_x)\) são usadas para encontrar um vetor a partir de seus componentes perpendiculares, ou seja, ir de\(\displaystyle A_x\)\(\displaystyle A\) e\(\displaystyle A_y\) para\(\displaystyle θ\) e. Ambos os processos são cruciais para os métodos analíticos de adição e subtração de vetores.

    Adicionando vetores usando métodos analíticos

    Para ver como adicionar vetores usando componentes perpendiculares, considere a Figura, na qual os vetores\(\displaystyle A\)\(\displaystyle B\) são adicionados para produzir a resultante\(\displaystyle R\).

    Dois vetores A e B são mostrados. A cauda do vetor B está na cabeça do vetor A e a cauda do vetor A está na origem. Ambos os vetores estão no primeiro quadrante. O R resultante desses dois vetores que se estendem da cauda do vetor A até a cabeça do vetor B também é mostrado.
    Figura\(\PageIndex{5}\): Vetores\(\displaystyle A\) and\(\displaystyle B\) are two legs of a walk, and \(\displaystyle R\) is the resultant or total displacement. You can use analytical methods to determine the magnitude and direction of \(\displaystyle R\).

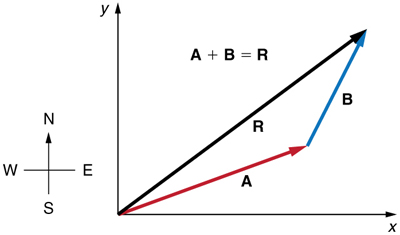
    E se\(\displaystyle A\) and \(\displaystyle B\) represent two legs of a walk (two displacements), then \(\displaystyle R\) is the total displacement. The person taking the walk ends up at the tip of R. There are many ways to arrive at the same point. In particular, the person could have walked first in the x-direction and then in the y-direction. Those paths are the x- and y-components of the resultant, \(\displaystyle R_x\) and \(\displaystyle R_y\). If we know \(\displaystyle R_x\) and \(\displaystyle R_y\), we can find \(\displaystyle R\) and \(\displaystyle θ\) using the equations \(\displaystyle A=\sqrt{A_x^2+A_y^2}\) and \(\displaystyle θ=tan^{–1}(A_y/A_x)\). When you use the analytical method of vector addition, you can determine the components or the magnitude and direction of a vector.

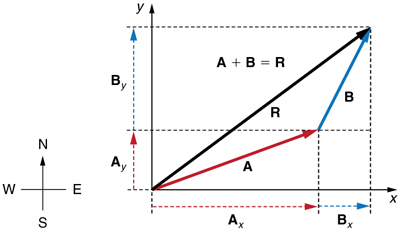
    Etapa 1. Identifique os eixos x e y que serão usados no problema. Em seguida, encontre os componentes de cada vetor a serem adicionados ao longo dos eixos perpendiculares escolhidos. Use as equações\(\displaystyle A_x=Acosθ\) and \(\displaystyle A_y=Asinθ\) to find the components. In Figure, these components are \(\displaystyle A_x, A_y, B_x\), and \(\displaystyle B_y\). The angles that vectors \(\displaystyle A\) and \(\displaystyle B\) make with the x-axis are \(\displaystyle θ_A\) and \(\displaystyle θ_B\), respectively.

    Dois vetores A e B são mostrados. A cauda do vetor B está na cabeça do vetor A e a cauda do vetor A está na origem. Ambos os vetores estão no primeiro quadrante. O R resultante desses dois vetores que se estendem da cauda do vetor A até a cabeça do vetor B também é mostrado. Os componentes horizontais e verticais dos vetores A e B são mostrados com a ajuda de linhas pontilhadas. Os vetores rotulados como A sub x e A sub y são os componentes do vetor A, e B sub x e B sub y como os componentes do vetor B..
    Figura\(\PageIndex{6}\): Para adicionar vetores\(\displaystyle A\) and \(\displaystyle B\), first determine the horizontal and vertical components of each vector. These are the dotted vectors \(\displaystyle A_x, A_y, B_x\) and \(\displaystyle B-y\) shown in the image.

    Etapa 2. Encontre os componentes da resultante ao longo de cada eixo adicionando os componentes dos vetores individuais ao longo desse eixo. Ou seja, conforme mostrado na Figura,

    \(\displaystyle R_x=A_x+B_x\)

    e

    \(\displaystyle R_y=A_y+B_y.\)

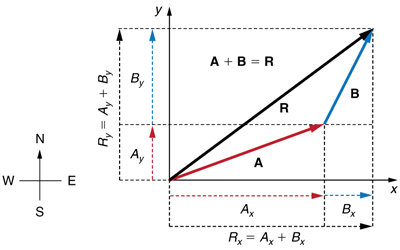
    Dois vetores A e B são mostrados. A cauda do vetor B está na cabeça do vetor A e a cauda do vetor A está na origem. Ambos os vetores estão no primeiro quadrante. O R resultante desses dois vetores que se estendem da cauda do vetor A até a cabeça do vetor B também é mostrado. Os vetores A e B são resolvidos nos componentes horizontal e vertical mostrados como linhas pontilhadas paralelas ao eixo x e ao eixo y, respectivamente. Os componentes horizontais do vetor A e do vetor B são rotulados como A sub x e B sub x e o componente horizontal do R resultante é rotulado em R sub x e é igual a A sub x mais B sub x. Os componentes verticais do vetor A e do vetor B são rotulados como A sub y e B sub y e os componentes verticais do R resultante é rotulado como R sub y é igual a A sub y mais B sub y.
    Figura\(\PageIndex{7}\): A magnitude dos vetores\(\displaystyle A_x\) and \(\displaystyle B_x\) add to give the magnitude \(\displaystyle R_x\) of the resultant vector in the horizontal direction. Similarly, the magnitudes of the vectors \(\displaystyle A_y\) and \(\displaystyle B_y\) add to give the magnitude \(\displaystyle R_y\) of the resultant vector in the vertical direction.

    Componentes ao longo do mesmo eixo, digamos o eixo x, são vetores na mesma linha e, portanto, podem ser adicionados uns aos outros como números comuns. O mesmo vale para componentes ao longo do eixo y. (Por exemplo, uma caminhada de 9 quarteirões para o leste pode ser feita em duas etapas, os primeiros 3 quarteirões a leste e os segundos 6 quarteirões a leste, totalizando 9, porque eles estão na mesma direção.) Portanto, a resolução de vetores em componentes ao longo de eixos comuns facilita a adição deles. Agora que os componentes de R são conhecidos, sua magnitude e direção podem ser encontradas.

    Etapa 3. Para obter a magnitude\(\displaystyle R\) of the resultant, use the Pythagorean theorem:

    \(\displaystyle R=\sqrt{R^2_x+R^2_y}\).

    Etapa 4. Para obter a direção do resultado:

    \(\displaystyle θ=tan^{−1}(R_y/R_x)\).

    O exemplo a seguir ilustra essa técnica para adicionar vetores usando componentes perpendiculares.

    Exemplo\(\displaystyle \PageIndex{1}\): Adding Vectors Using Analytical Methods

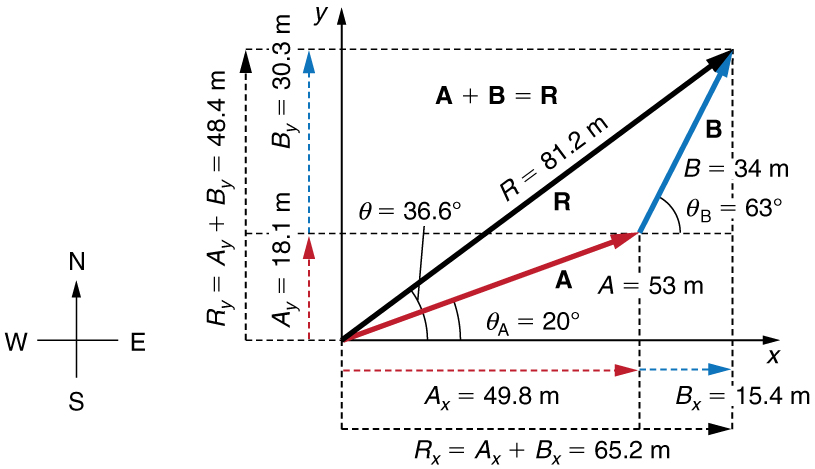
    Adicione o vetor\(\displaystyle A\) ao vetor\(\displaystyle B\) mostrado na Figura, usando componentes perpendiculares ao longo dos eixos x e y. Os eixos x e y estão ao longo das direções leste-oeste e norte-sul, respectivamente. O vetor\(\displaystyle A\) representa a primeira etapa de uma caminhada na qual uma pessoa caminha\(\displaystyle 53.0 m\) na direção\(\displaystyle 20.0º\) norte do leste. O vetor\(\displaystyle B\) representa a segunda perna, um deslocamento de\(\displaystyle 34.0 m\) na direção\(\displaystyle 63.0º\) norte do leste.

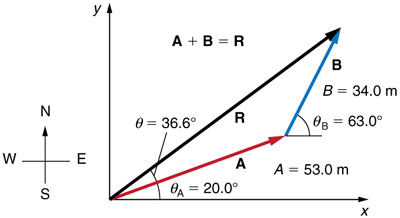
    Dois vetores A e B são mostrados. A cauda do vetor A está na origem. Ambos os vetores estão no primeiro quadrante. O vetor A tem magnitude cinquenta e três unidades e está inclinado em um ângulo de vinte graus em relação à horizontal. Da cabeça do vetor A, outro vetor B de magnitude 34 unidades é desenhado e inclinado em um ângulo de sessenta e três graus com a horizontal. A resultante de dois vetores é desenhada da cauda do vetor A até a cabeça do vetor B.
    Figura\(\PageIndex{8}\):\(\displaystyle A\) O vetor tem magnitude\(\displaystyle 53.0 m\) e direção\(\displaystyle 20.0º\) ao norte do eixo x. O vetor B tem magnitude\(\displaystyle 34.0 m\) e direção\(\displaystyle 63.0º\) ao norte do eixo x. Você pode usar métodos analíticos para determinar a magnitude e a direção de\(\displaystyle R\).

    Estratégia

    Os componentes de\(\displaystyle A\) e\(\displaystyle B\) ao longo dos eixos x e y representam caminhar para o leste e para o norte para chegar ao mesmo ponto final. Uma vez encontrados, eles são combinados para produzir o resultado.

    Solução

    Seguindo o método descrito acima, primeiro encontramos os componentes de\(\displaystyle A\) e\(\displaystyle B\) ao longo dos eixos x e y. Observe isso\(\displaystyle A=53.0 m, θ_A=20.0º, B=34.0 m,\)\(\displaystyle θ_B=63.0º\) e. Encontramos os componentes x- usando\(\displaystyle A_x=Acosθ\), o que dá

    \(\displaystyle A_x=Acosθ_A=(53.0 m)(cos 20.0º)(53.0 m)(0.940)=49.8 m\)

    e

    \(\displaystyle B_x=Bcosθ_B=(34.0 m)(cos 63.0º)(34.0 m)(0.454)=15.4 m.\)

    Da mesma forma, os componentes y- são encontrados usando\(\displaystyle A_y=Asinθ_A\):

    \(\displaystyle A_y=Asinθ_A=(53.0 m)(sin 20.0º)(53.0 m)(0.342)=18.1 m\)

    e

    \(\displaystyle B_y=Bsinθ_B=(34.0 m)(sin 63.0º)(34.0 m)(0.891)=30.3 m.\)

    Os componentes x e y da resultante são, portanto,

    \(\displaystyle R_x=A_x+B_x=49.8 m+15.4 m=65.2 m\)

    e

    \(\displaystyle R_y=A_y+B_y=18.1 m+30.3 m=48.4 m.\)

    Agora podemos encontrar a magnitude da resultante usando o teorema de Pitágoras:

    \(\displaystyle R=\sqrt{R^2_x+R^2_y}=\sqrt{(65.2)^2+(48.4)^2m}\)

    para que

    \(\displaystyle R=81.2 m.\)

    Finalmente, encontramos a direção da resultante:

    \(\displaystyle θ=tan^{−1}(R_y/R_x)=+tan^{−1}(48.4/65.2).\)

    Assim,

    \(\displaystyle θ=tan^{−1}(0.742)=36.6º.\)

    A adição de dois vetores A e B é mostrada. O vetor A tem magnitude cinquenta e três unidades e está inclinado em um ângulo de vinte graus em relação à horizontal. O vetor B é de magnitude trinta e quatro unidades e está inclinado em um ângulo de sessenta e três graus em relação à horizontal. Os componentes do vetor A são mostrados como vetores pontilhados A X é igual a quarenta e nove pontos oito metros ao longo do eixo x e A Y é igual a dezoito ponto um metro ao longo do eixo Y. Os componentes do vetor B também são mostrados como vetores pontilhados B X é igual a quinze pontos quatro metros e B Y é igual a trinta pontos três metros. O componente horizontal do R X resultante é igual a A X mais B X é igual a sessenta e cinco pontos e dois metros. O componente vertical do R Y resultante é igual a A Y mais B Y é igual a quarenta e oito pontos quatro metros. A magnitude da resultante de dois vetores é oitenta e um ponto e dois metros. A direção do R resultante está em trinta e seis pontos e seis graus do vetor A no sentido anti-horário.
    Figura\(\PageIndex{9}\): Usando métodos analíticos, vemos que a magnitude de\(\displaystyle R\) is\(\displaystyle 81.2 m\) e sua direção estão\(\displaystyle 36.6º\) ao norte do leste.

    Discussão

    Este exemplo ilustra a adição de vetores usando componentes perpendiculares. A subtração vetorial usando componentes perpendiculares é muito similar — é apenas a adição de um vetor negativo.

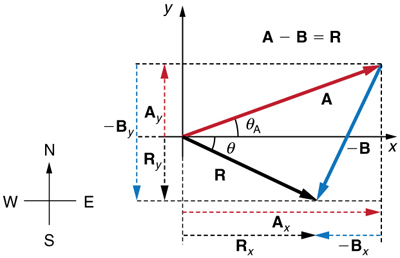
    A subtração de vetores é realizada pela adição de um vetor negativo. Isso é,\(\displaystyle A−B≡A+(–B)\). Assim, o método para a subtração de vetores usando componentes perpendiculares é idêntico ao de adição. Os componentes do\(\displaystyle –B\) são os negativos dos componentes do\(\displaystyle B\). Os componentes x e y da resultante\(\displaystyle A−B = R\) são, portanto,

    \(\displaystyle R_x=A_x+(–B_x)\)

    e

    \(\displaystyle R_y=A_y+(–B_y)\)

    e o resto do método descrito acima é idêntico ao da adição. (Veja a Figura.)

    Analisar vetores usando componentes perpendiculares é muito útil em muitas áreas da física, porque quantidades perpendiculares geralmente são independentes umas das outras. O próximo módulo, Projectile Motion, é um dos muitos em que o uso de componentes perpendiculares ajuda a tornar a imagem clara e simplifica a física.

    Nesta figura, a subtração de dois vetores A e B é mostrada. Um vetor A de cor vermelha é inclinado em um ângulo teta A em relação ao positivo do eixo x. Da cabeça do vetor A, um vetor azul negativo B é desenhado. O vetor B está no oeste da direção sul. A resultante do vetor A e do vetor negativo B é mostrada como um vetor R preto da cauda do vetor A até a cabeça do vetor negativo B. O R resultante é inclinado para o eixo x em um ângulo teta abaixo do eixo x. Os componentes dos vetores também são mostrados ao longo dos eixos de coordenadas como linhas pontilhadas de suas respectivas cores.
    Figura. Os componentes do\(\displaystyle –B\) são os negativos dos componentes do\(\displaystyle B\). O método de subtração é o mesmo da adição.

    EXPLORAÇÕES PHET: ADIÇÃO DE VETORES

    Saiba como adicionar vetores. Arraste vetores para um gráfico, altere seu comprimento e ângulo e some-os juntos. A magnitude, o ângulo e os componentes de cada vetor podem ser exibidos em vários formatos.

    PhET_Icon.png
    Figura\(\PageIndex{11}\): Adição de vetores

    Resumo

    • O método analítico de adição e subtração de vetores envolve o uso do teorema de Pitágoras e identidades trigonométricas para determinar a magnitude e a direção de um vetor resultante.
    • As etapas para adicionar vetores\(\displaystyle A\) e\(\displaystyle B\) usar o método analítico são as seguintes:

    Etapa 1: Determine o sistema de coordenadas dos vetores. Em seguida, determine os componentes horizontal e vertical de cada vetor usando as equações

    \(\displaystyle A_x=Acosθ\)
    \(\displaystyle B_x=Bcosθ\)

    e

    \(\displaystyle A_y=Asinθ\)
    \(\displaystyle B_y=Bsinθ.\)

    Etapa 2: Adicione os componentes horizontal e vertical de cada vetor para determinar os componentes Rx e Ry do vetor resultante, R:

    \(\displaystyle R_x=A_x+B_x\)

    e

    \(\displaystyle R_y=A_y+B_y\).

    Etapa 3: Use o teorema de Pitágoras para determinar a magnitude, R, do vetor resultante R:

    \(\displaystyle R=\sqrt{R^2_x+R^2_y}\).

    Etapa 4: Use uma identidade trigonométrica para determinar a direção,\(\displaystyle θ\), de R:

    \(\displaystyle θ=tan^{−1}(R_y/R_x)\).

    Glossário

    método analítico
    o método de determinação da magnitude e direção de um vetor resultante usando o teorema de Pitágoras e identidades trigonométricas