3.2: Adição e subtração de vetores - métodos gráficos
- Page ID
- 194381
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Entenda as regras de adição, subtração e multiplicação de vetores.
- Aplique métodos gráficos de adição e subtração de vetores para determinar o deslocamento de objetos em movimento.
Adição e subtração de vetores: métodos gráficos
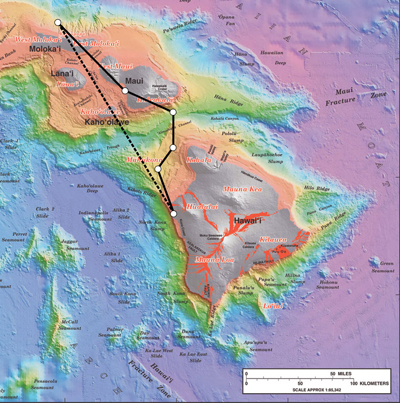
Vetores em duas dimensões
Um vetor é uma quantidade que tem magnitude e direção. Deslocamento, velocidade, aceleração e força, por exemplo, são todos vetores. Em movimentos unidimensionais ou em linha reta, a direção de um vetor pode ser dada simplesmente por um sinal de mais ou menos. Em duas dimensões (2-d), no entanto, especificamos a direção de um vetor em relação a algum quadro de referência (ou seja, sistema de coordenadas), usando uma seta com comprimento proporcional à magnitude do vetor e apontando na direção do vetor.
A figura mostra essa representação gráfica de um vetor, usando como exemplo o deslocamento total da pessoa que caminha em uma cidade considerada em Cinemática em Duas Dimensões: Uma Introdução. Usaremos a notação de que um símbolo em negrito\(D\), como, representa um vetor. Sua magnitude é representada pelo símbolo em\(D\) itálico e sua direção por\(θ\).
VETORES NESTE TEXTO
Neste texto, representaremos um vetor com uma variável em negrito. Por exemplo, representaremos a força de quantidade com o vetor\(F\), que tem magnitude e direção. A magnitude do vetor será representada por uma variável em itálico\(F\), como, e a direção da variável será dada por um ângulo\(θ\).
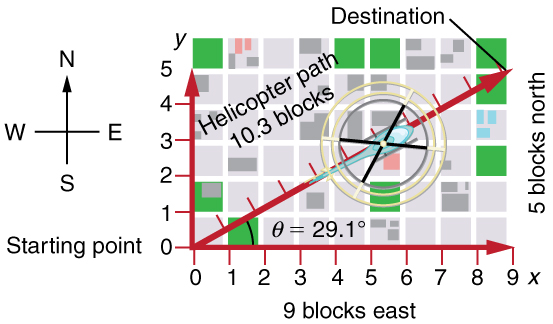
Figura\(\PageIndex{2}\): Uma pessoa caminha 9 quarteirões ao leste e 5 ao norte. O deslocamento é de 10,3 blocos em um ângulo de 0,1 º ao norte do leste.
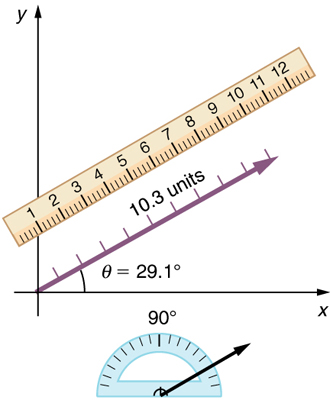
Adição de vetores: Método da cabeça à cauda
O método cabeça a ponta é uma forma gráfica de adicionar vetores, descrita na Figura abaixo e nas etapas a seguir. A cauda do vetor é o ponto inicial do vetor, e a cabeça (ou ponta) de um vetor é a extremidade final e pontiaguda da seta.
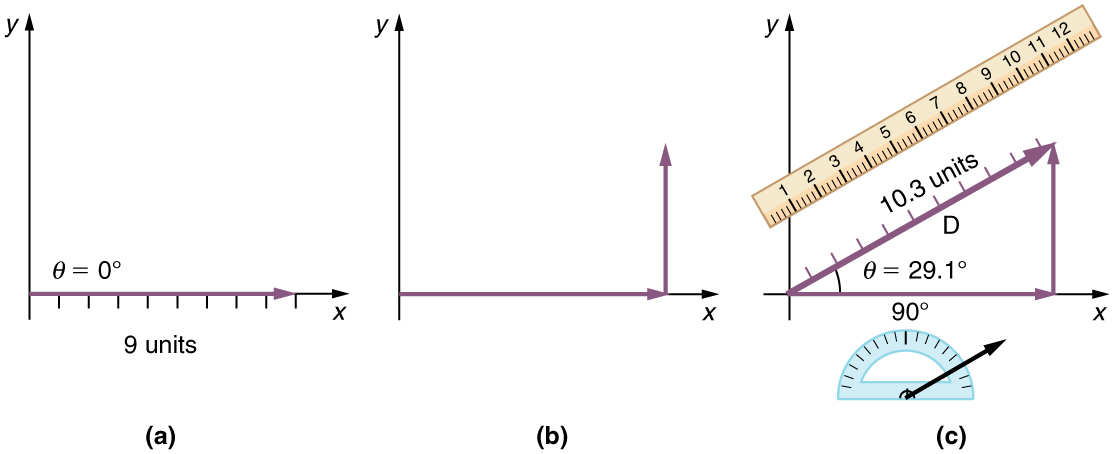
Etapa 1. Desenhe uma seta para representar o primeiro vetor (9 blocos a leste) usando uma régua e um transferidor.
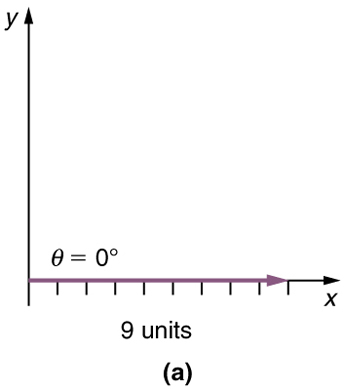
Etapa 2. Agora desenhe uma seta para representar o segundo vetor (5 blocos ao norte). Coloque a cauda do segundo vetor na cabeça do primeiro vetor.
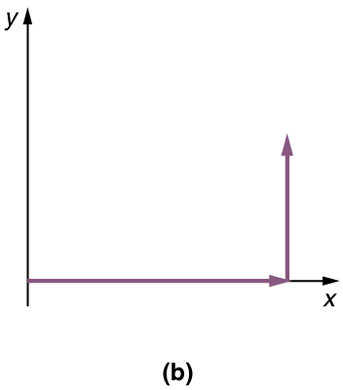
Etapa 3. Se houver mais de dois vetores, continue esse processo para que cada vetor seja adicionado. Observe que, em nosso exemplo, temos apenas dois vetores, então terminamos de colocar as setas da ponta à cauda.
Etapa 4. Desenhe uma flecha da cauda do primeiro vetor até a cabeça do último vetor. Essa é a resultante, ou a soma, dos outros vetores.
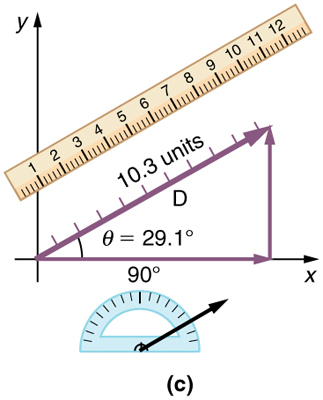
Etapa 5. Para obter a magnitude da resultante, meça seu comprimento com uma régua. (Observe que, na maioria dos cálculos, usaremos o teorema de Pitágoras para determinar esse comprimento.)
Etapa 6. Para obter a direção da resultante, meça o ângulo que ela faz com o quadro de referência usando um transferidor. (Observe que, na maioria dos cálculos, usaremos relações trigonométricas para determinar esse ângulo.)
A adição gráfica de vetores é limitada em precisão apenas pela precisão com que os desenhos podem ser feitos e pela precisão das ferramentas de medição. É válido para qualquer número de vetores.
Exemplo\(\PageIndex{1}\):Adding Vectors Graphically Using the Head-to-Tail Method: A Woman Takes a Walk
Use a técnica gráfica para adicionar vetores para encontrar o deslocamento total de uma pessoa que percorre os três caminhos a seguir (deslocamentos) em um campo plano. Primeiro, ela caminha 25,0 m na direção norte do leste. Em seguida, ela caminha 23,0 m em direção ao norte do leste. Finalmente, ela vira e caminha 32,0 m em uma direção 68,0° ao sul do leste.
Estratégia
Represente graficamente cada vetor de deslocamento com uma seta, rotulando o primeiro, o segundo e o terceiro, tornando os comprimentos proporcionais à distância e às direções especificadas em relação a uma linha leste-oeste. O método da cabeça à cauda descrito acima fornecerá uma maneira de determinar a magnitude e a direção do deslocamento resultante, indicado.
Solução
(1) Desenhe os três vetores de deslocamento.
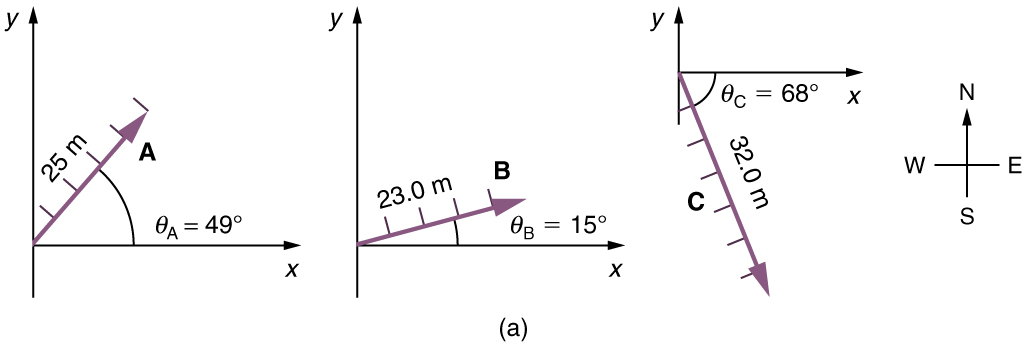
(2) Coloque os vetores da cabeça à cauda, mantendo sua magnitude e direção iniciais.
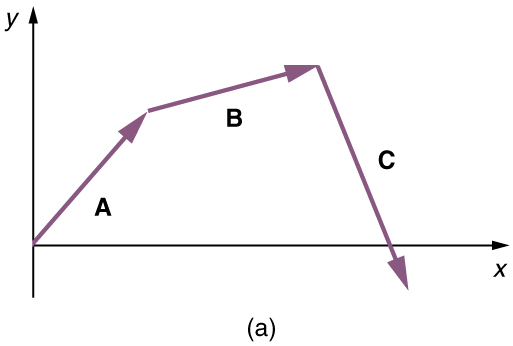
(3) Desenhe o vetor resultante,.
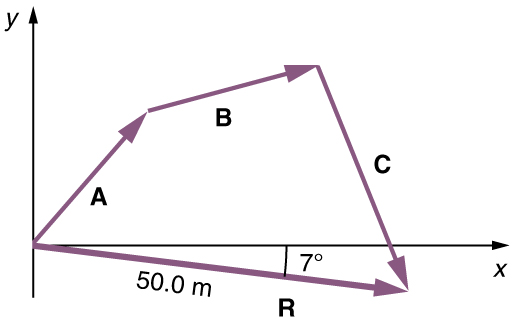
(4) Use uma régua para medir a magnitude de e um transferidor para medir a direção de. Embora a direção do vetor possa ser especificada de várias maneiras, a maneira mais fácil é medir o ângulo entre o vetor e o eixo horizontal ou vertical mais próximo. Como o vetor resultante está ao sul do eixo apontador para o leste, viramos o transferidor de cabeça para baixo e medimos o ângulo entre o eixo leste e o vetor.
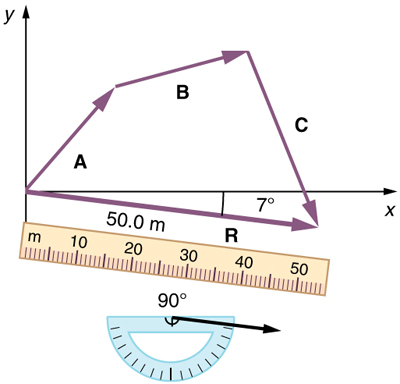
Nesse caso, o deslocamento total é visto como tendo uma magnitude de 50,0 m e está na direção sul do leste. Usando sua magnitude e direção, esse vetor pode ser expresso como = 50,0 m e = 7. 0 º sul do leste.
Discussão
O método gráfico completo de adição de vetores funciona para qualquer número de vetores. Também é importante observar que a resultante é independente da ordem em que os vetores são adicionados. Portanto, podemos adicionar os vetores em qualquer ordem, conforme ilustrado na Figura, e ainda obteremos a mesma solução.
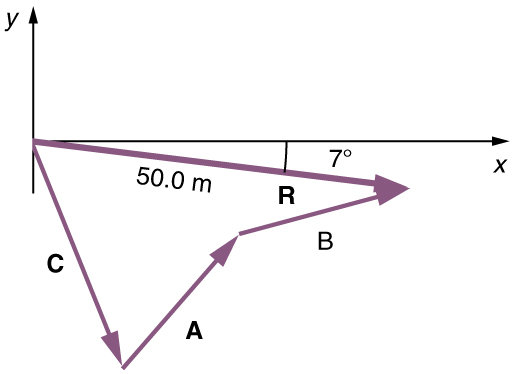
Aqui, vemos que quando os mesmos vetores são adicionados em uma ordem diferente, o resultado é o mesmo. Essa característica é verdadeira em todos os casos e é uma característica importante dos vetores. A adição de vetores é comutativa. Os vetores podem ser adicionados em qualquer ordem.
\(A+B=B+A.\)
(Isso também vale para a adição de números comuns — você obtém o mesmo resultado adicionando + 3 ou + 2, por exemplo).
Subtração vetorial
A subtração vetorial é uma extensão direta da adição vetorial. Para definir subtração (digamos que queremos subtrair de, escrito — B), devemos primeiro definir o que queremos dizer com subtração. O negativo de um vetor é definido como; ou seja, graficamente, o negativo de qualquer vetor tem a mesma magnitude, mas na direção oposta, conforme mostrado na Figura. Em outras palavras, tem o mesmo comprimento que, mas aponta na direção oposta. Essencialmente, simplesmente invertemos o vetor para que ele aponte na direção oposta.
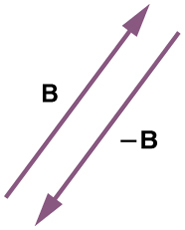
A subtração do vetor do vetor é então simplesmente definida como a adição de a. Observe que a subtração vetorial é a adição de um vetor negativo. A ordem de subtração não afeta os resultados.
Isso é análogo à subtração de escalares (onde, por exemplo, (—2)). Novamente, o resultado é independente da ordem em que a subtração é feita. Quando os vetores são subtraídos graficamente, as técnicas descritas acima são usadas, conforme ilustrado no exemplo a seguir.
Exemplo\(\PageIndex{1}\):Subtracting Vectors Graphically: A Woman Sailing a Boat
Uma mulher navegando em um barco à noite está seguindo as instruções para uma doca. As instruções são para navegar primeiro 27,5 m em uma direção norte ou leste a partir de sua localização atual e depois viajar 30,0 m na direção norte do leste (ou oeste do norte). Se a mulher cometer um erro e viajar na direção oposta na segunda etapa da viagem, onde ela vai parar? Compare essa localização com a localização da doca.
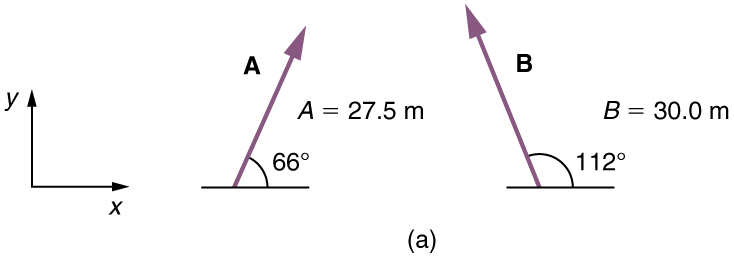
Estratégia
Podemos representar a primeira etapa da viagem com um vetor e a segunda etapa da viagem com um vetor. A doca está localizada em um local + B. Se a mulher viajar por engano na direção oposta na segunda etapa da viagem, ela percorrerá uma distância (30,0 m) na direção — 112 º = 68º ao sul do leste. Nós representamos isso como, conforme mostrado abaixo. O vetor tem a mesma magnitude, mas está na direção oposta. Assim, ela acabará em um local + (— B) ou — B.
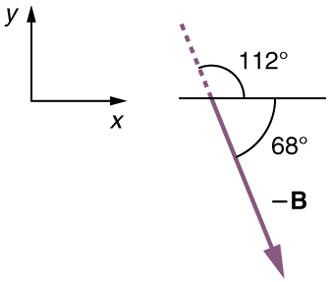
Vamos realizar a adição vetorial para comparar a localização da doca, + B, com o local em que a mulher chega por engano, + (— B).
Solução
(1) Para determinar o local em que a mulher chega por acidente, desenhe vetores e.
(2) Coloque os vetores da cabeça à cauda.
(3) Desenhe o vetor resultante.
(4) Use uma régua e um transferidor para medir a magnitude e a direção de.
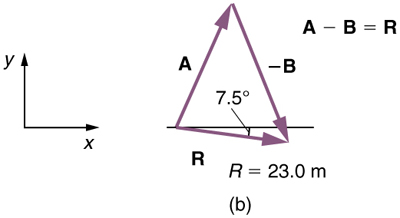
Nesse caso, = 23. 0 m e = 7. 5º ao sul do leste.
(5) Para determinar a localização da doca, repetimos esse método para adicionar vetores e. Obtemos o vetor resultante ':

Nesse caso = 52,9 m e = 90,1 º ao norte do leste.
Podemos ver que a mulher ficará a uma distância significativa do cais se viajar na direção oposta na segunda etapa da viagem.
Discussão
Como a subtração de um vetor é o mesmo que a adição de um vetor na direção oposta, o método gráfico de subtração de vetores funciona da mesma forma que para adição.
Multiplicação de vetores e escalares
Se decidirmos caminhar três vezes mais longe na primeira etapa da viagem considerada no exemplo anterior, então caminharíamos × 27. 5 m, ou 82,5 m, em uma direção . 0 º norte do leste. Este é um exemplo de multiplicação de um vetor por um escalar positivo. Observe que a magnitude muda, mas a direção permanece a mesma.
Se o escalar for negativo, multiplicar um vetor por ele altera a magnitude do vetor e dá ao novo vetor a direção oposta. Por exemplo, se você multiplicar por —2, a magnitude dobra, mas a direção muda. Podemos resumir essas regras da seguinte maneira: Quando o vetor é multiplicado por um escalar,
- a magnitude do vetor se torna o valor absoluto de,
- se for positivo, a direção do vetor não muda,
- se for negativo, a direção é invertida.
No nosso caso, = 3 e = 27,5 m. Os vetores são multiplicados por escalares em muitas situações. Observe que a divisão é o inverso da multiplicação. Por exemplo, dividir por 2 é o mesmo que multiplicar pelo valor (1/2). As regras para multiplicação de vetores por escalares são as mesmas para divisão; basta tratar o divisor como um escalar entre 0 e 1.
Resolvendo um vetor em componentes
Nos exemplos acima, adicionamos vetores para determinar o vetor resultante. Em muitos casos, no entanto, precisaremos fazer o oposto. Precisaremos pegar um único vetor e descobrir quais outros vetores somados o produzem. Na maioria dos casos, isso envolve determinar os componentes perpendiculares de um único vetor, por exemplo, os componentes x e y, ou os componentes norte-sul e leste-oeste.
Por exemplo, podemos saber que o deslocamento total de uma pessoa andando em uma cidade é de 10,3 quarteirões em uma direção 0,0º ao norte do leste e queremos descobrir quantos quarteirões leste e norte tiveram que ser percorridos. Esse método é chamado de encontrar os componentes (ou partes) do deslocamento nas direções leste e norte, e é o inverso do processo seguido para encontrar o deslocamento total. É um exemplo de como encontrar os componentes de um vetor. Existem muitas aplicações em física em que isso é uma coisa útil de se fazer. Veremos isso em breve em Projectile Motion, e muito mais quando abordarmos forças em Dynamics: Newton's Laws of Motion. A maioria deles envolve encontrar componentes ao longo de eixos perpendiculares (como norte e leste), de modo que triângulos retos estejam envolvidos. As técnicas analíticas apresentadas em Adição e Subtração de Vetores: Métodos Analíticos são ideais para encontrar componentes vetoriais.
PHET EXPLORATIONS: JOGO DE LABIRINTO
Aprenda sobre posição, velocidade e aceleração na “Arena da Dor”. Use a seta verde para mover a bola. Adicione mais paredes à arena para tornar o jogo mais difícil. Tente estabelecer uma meta o mais rápido possível.

- O método gráfico de adicionar vetores envolve desenhar vetores em um gráfico e adicioná-los usando o método cabeça a cauda. O vetor resultante é definido de forma que + B = R. A magnitude e a direção de são então determinadas com uma régua e um transferidor, respectivamente.
- O método gráfico de subtração do vetor envolve a adição do oposto do vetor, que é definido como B. Nesse caso, — B = A + (— B) = R. Em seguida, o método de adição direto é seguido da maneira usual para obter o vetor resultante.
- A adição de vetores é comutativa de tal forma que + B = B + A.
- O método de adição direta de vetores envolve desenhar o primeiro vetor em um gráfico e, em seguida, colocar a cauda de cada vetor subsequente na cabeça do vetor anterior. O vetor resultante é então desenhado da cauda do primeiro vetor até a cabeça do vetor final.
- Se um vetor for multiplicado por uma quantidade escalar, a magnitude do produto é dada por . Se for positivo, a direção do produto aponta na mesma direção que; se for negativo, a direção do produto aponta na direção oposta a.
Glossário
- componente (de um vetor 2-d)
- uma parte de um vetor que aponta na direção vertical ou horizontal; cada vetor 2-d pode ser expresso como uma soma de dois componentes vetoriais verticais e horizontais
- comutativo
- refere-se à intercambiabilidade da ordem em uma função; a adição vetorial é comutativa porque a ordem na qual os vetores são somados não afeta a soma final
- direção (de um vetor)
- a orientação de um vetor no espaço
- cabeça (de um vetor)
- o ponto final de um vetor; a localização da ponta da seta do vetor; também conhecida como a “ponta”
- método cabeça a cauda
- um método de adição de vetores em que a cauda de cada vetor é colocada na cabeça do vetor anterior
- magnitude (de um vetor)
- o comprimento ou tamanho de um vetor; magnitude é uma quantidade escalar
- resultante
- a soma de dois ou mais vetores
- vetor resultante
- a soma vetorial de dois ou mais vetores
- escalar
- uma quantidade com magnitude, mas sem direção
- cauda
- o ponto inicial de um vetor; oposto à cabeça ou ponta da seta


