3.1: Cinemática em duas dimensões - uma introdução

Objetivos de

Ao final desta seção, você poderá:

• Observe que o movimento em duas dimensões consiste em componentes horizontais e verticais.
• Entenda a independência dos vetores horizontais e verticais em movimentos bidimensionais.

Figura\(\PageIndex{1}\): Caminhantes e motoristas em uma cidade como Nova York raramente conseguem viajar em linha reta para chegar a seus destinos. Em vez disso, eles devem seguir estradas e calçadas, criando caminhos bidimensionais em ziguezague. (crédito: Margaret W. Carruthers)

Movimento bidimensional: caminhando em uma cidade

Suponha que você queira caminhar de um ponto a outro em uma cidade com blocos quadrados uniformes, conforme ilustrado na Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\): Um pedestre percorre um caminho bidimensional entre dois pontos em uma cidade. Nesta cena, todos os blocos são quadrados e têm o mesmo tamanho.

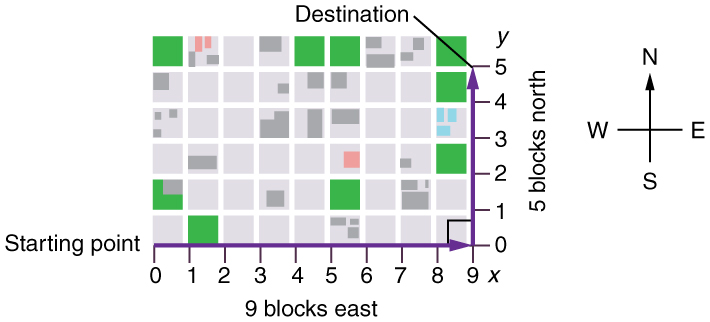
O caminho em linha reta que um helicóptero pode voar está bloqueado para você como pedestre e, portanto, você é forçado a seguir um caminho bidimensional, como o mostrado. Você anda 14 quarteirões ao todo, 9 para o leste seguido por 5 para o norte. Qual é a distância em linha reta?

Um velho ditado afirma que a menor distância entre dois pontos é uma linha reta. As duas etapas da viagem e o caminho em linha reta formam um triângulo reto, e assim o teorema de Pitágoras,

\[a^2 + b^2 = c^2\]

pode ser usado para encontrar a distância em linha reta.

Figura\(\PageIndex{3}\): O teorema de Pitágoras relaciona o comprimento das pernas de um triângulo reto, rotulado\(a\) e\(b\), com a hipotenusa, rotulado\(c\). O relacionamento é dado por:\(a^2+ b^2= c^2\). Isso pode ser reescrito, resolvendo\(c : c =\sqrt{a^2+b^2}\).

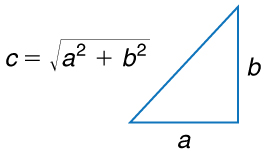
A hipotenusa do triângulo é o caminho em linha reta e, neste caso, seu comprimento em unidades de quarteirões da cidade é\(\sqrt{(9 blocks)^2+ (5 blocks)^2}= 10.3 blocks\) consideravelmente menor do que os 14 quarteirões que você andou. (Observe que estamos usando três números significativos na resposta. Embora pareça que “9” e “5” tenham apenas um dígito significativo, eles são números discretos. Nesse caso, “9 blocos” é o mesmo que “9,0 ou 9,00 blocos”. Decidimos usar três números significativos na resposta para mostrar o resultado com mais precisão.)

Figura\(\PageIndex{4}\): O caminho em linha reta seguido por um helicóptero entre os dois pontos é menor do que os 14 quarteirões percorridos pelo pedestre. Todos os blocos são quadrados e do mesmo tamanho.

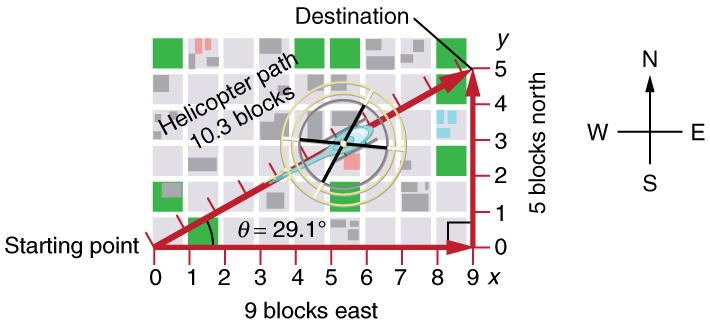
O fato de a distância em linha reta (10,3 blocos) na Figura ser menor que a distância total percorrida (14 blocos) é um exemplo de uma característica geral dos vetores. (Lembre-se de que vetores são quantidades que têm magnitude e direção.)

Quanto à cinemática unidimensional, usamos setas para representar vetores. O comprimento da seta é proporcional à magnitude do vetor. O comprimento da seta é indicado por marcas de hash na Figura e na Figura. A seta aponta na mesma direção do vetor. Para movimentos bidimensionais, o caminho de um objeto pode ser representado com três vetores: um vetor mostra o caminho em linha reta entre os pontos inicial e final do movimento, um vetor mostra o componente horizontal do movimento e um vetor mostra o componente vertical do movimento. Os componentes horizontal e vertical do movimento se somam para dar o caminho em linha reta. Por exemplo, observe os três vetores na Figura. O primeiro representa um deslocamento de 9 quarteirões para o leste. O segundo representa um deslocamento de 5 quarteirões para o norte. Esses vetores são adicionados para dar o terceiro vetor, com um deslocamento total de 10,3 blocos. O terceiro vetor é o caminho em linha reta entre os dois pontos. Observe que neste exemplo, os vetores que estamos adicionando são perpendiculares entre si e, portanto, formam um triângulo reto. Isso significa que podemos usar o teorema de Pitágoras para calcular a magnitude do deslocamento total. (Observe que não podemos usar o teorema de Pitágoras para adicionar vetores que não sejam perpendiculares. Desenvolveremos técnicas para adicionar vetores com qualquer direção, não apenas aqueles perpendiculares entre si, em Adição e Subtração de Vetores: Métodos Gráficos e Adição e Subtração de Vetores: Métodos Analíticos.)

A independência dos movimentos perpendiculares

A pessoa que segue o caminho mostrado na Figura caminha para o leste e depois para o norte (duas direções perpendiculares). A distância que ele ou ela caminha para o leste só é afetada por seu movimento em direção ao leste. Da mesma forma, a distância que ele ou ela caminha para o norte só é afetada por seu movimento em direção ao norte.

INDEPENDÊNCIA DO MOVIMENTO

Os componentes horizontal e vertical do movimento bidimensional são independentes um do outro. Qualquer movimento na direção horizontal não afeta o movimento na direção vertical e vice-versa.

Isso é verdade em um cenário simples, como o de caminhar primeiro em uma direção e depois em outra. Também se aplica a movimentos mais complicados que envolvem movimento em duas direções ao mesmo tempo. Por exemplo, vamos comparar os movimentos de duas bolas de beisebol. Uma bola de beisebol é retirada do repouso. No mesmo instante, outro é lançado horizontalmente da mesma altura e segue um caminho curvo. Um estroboscópio capturou as posições das bolas em intervalos de tempo fixos à medida que elas caem.

Figura\(\PageIndex{5}\): Isso mostra os movimentos de duas bolas idênticas: uma cai do repouso e a outra tem uma velocidade horizontal inicial. Cada posição subsequente é um intervalo de tempo igual. As setas representam velocidades horizontais e verticais em cada posição. A bola à direita tem uma velocidade horizontal inicial, enquanto a bola à esquerda não tem velocidade horizontal. Apesar da diferença nas velocidades horizontais, as velocidades e posições verticais são idênticas para ambas as bolas. Isso mostra que os movimentos vertical e horizontal são independentes.

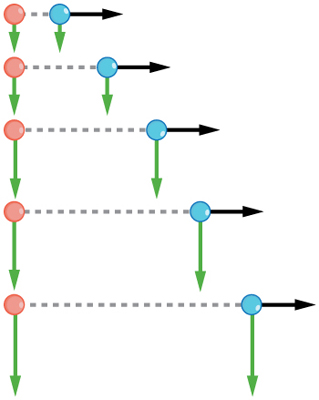
É notável que, para cada flash do estroboscópio, as posições verticais das duas bolas sejam as mesmas. Essa semelhança implica que o movimento vertical é independente de a bola estar ou não se movendo horizontalmente. (Supondo que não haja resistência do ar, o movimento vertical de um objeto em queda é influenciado somente pela gravidade e não por nenhuma força horizontal.) Um exame cuidadoso da bola lançada horizontalmente mostra que ela percorre a mesma distância horizontal entre os flashes. Isso se deve ao fato de que não há forças adicionais na bola na direção horizontal depois que ela é lançada. Esse resultado significa que a velocidade horizontal é constante e não é afetada nem pelo movimento vertical nem pela gravidade (que é vertical). Observe que esse caso é verdadeiro apenas para condições ideais. No mundo real, a resistência do ar afetará a velocidade das bolas em ambas as direções.

O caminho curvo bidimensional da bola lançada horizontalmente é composto por dois movimentos unidimensionais independentes (horizontal e vertical). A chave para analisar esse movimento, chamado movimento de projétil, é resolvê-lo (dividi-lo) em movimentos ao longo de direções perpendiculares. Resolver o movimento bidimensional em componentes perpendiculares é possível porque os componentes são independentes. Veremos como resolver vetores em Adição e Subtração de Vetores: Métodos Gráficos e Adição e Subtração de Vetores: Métodos Analíticos. Descobriremos que essas técnicas são úteis em muitas áreas da física.

EXPLORAÇÕES DE PHET: LADYBUG MOTION 2D

Saiba mais sobre vetores de posição, velocidade e aceleração. Mova a joaninha definindo a posição, velocidade ou aceleração e veja como os vetores mudam. Escolha movimento linear, circular ou elíptico e grave e reproduza o movimento para analisar o comportamento.

Figura\(\PageIndex{5}\): Ladybug Motion 2D

Resumo

• O caminho mais curto entre quaisquer dois pontos é uma linha reta. Em duas dimensões, esse caminho pode ser representado por um vetor com componentes horizontais e verticais.
• Os componentes horizontal e vertical de um vetor são independentes um do outro. O movimento na direção horizontal não afeta o movimento na direção vertical e vice-versa.

Glossário

vetor

uma quantidade que tem magnitude e direção; uma seta usada para representar quantidades com magnitude e direção