2.5: Equações de movimento para aceleração constante em uma dimensão
- Page ID
- 194263
objetivos de aprendizagem
Ao final desta seção, você poderá:
- Calcule o deslocamento de um objeto que não está acelerando, considerando a posição e a velocidade iniciais.
- Calcule a velocidade final de um objeto em aceleração, considerando a velocidade inicial, a aceleração e o tempo.
- Calcule o deslocamento e a posição final de um objeto em aceleração, considerando a posição inicial, a velocidade inicial, o tempo e a aceleração.
Talvez saibamos que quanto maior a aceleração de, digamos, um carro se afastando de um sinal de parada, maior o deslocamento em um determinado tempo. Mas não desenvolvemos uma equação específica que relacione aceleração e deslocamento. Nesta seção, desenvolvemos algumas equações convenientes para relações cinemáticas, partindo das definições de deslocamento, velocidade e aceleração já abordadas.

Notação: t, x, v, a
Primeiro, vamos fazer algumas simplificações na notação. Considerar o tempo inicial zero, como se o tempo fosse medido com um cronômetro, é uma ótima simplificação. Como o tempo decorrido é\(\displaystyle Δt=t_f−t_0\), tomar\(\displaystyle t_0=0\) significa isso\(\displaystyle Δt=t_f\), a última vez no cronômetro. Quando o tempo inicial é considerado zero, usamos o subscrito 0 para indicar os valores iniciais de posição e velocidade. Ou seja,\(\displaystyle x_0\) é a posição inicial e\(\displaystyle v_0\) é a velocidade inicial. Não colocamos assinaturas nos valores finais. Ou seja,\(\displaystyle t\) é o tempo final,\(\displaystyle x\) é a posição final e\(\displaystyle v\) é a velocidade final. Isso dá uma expressão mais simples para o tempo decorrido — agora,\(\displaystyle Δt=t\). Também simplifica a expressão de deslocamento, que é agora\(\displaystyle Δx=x−x_0\). Além disso, simplifica a expressão de mudança na velocidade, que é agora\(\displaystyle Δv=v−v_0\). Para resumir, usando a notação simplificada, com o tempo inicial considerado zero,
\(\displaystyle Δt=t\)
\(\displaystyle Δx=x−x_0\)
\(\displaystyle Δv=v−v_0\)
onde o subscrito 0 indica um valor inicial e a ausência de um subscrito indica um valor final em qualquer movimento que esteja sendo considerado.
Agora fazemos a importante suposição de que a aceleração é constante. Essa suposição nos permite evitar o uso do cálculo para encontrar a aceleração instantânea. Como a aceleração é constante, as acelerações média e instantânea são iguais. Ou seja,
\[\bar{a}=a=constant,\]
então usamos o símbolo a para aceleração em todos os momentos. Assumir que a aceleração seja constante não limita seriamente as situações que podemos estudar nem degrada a precisão do nosso tratamento. Por um lado, a aceleração é constante em um grande número de situações. Além disso, em muitas outras situações, podemos descrever com precisão o movimento assumindo uma aceleração constante igual à aceleração média desse movimento. Finalmente, em movimentos em que a aceleração muda drasticamente, como um carro acelerando até a velocidade máxima e depois freando até parar, o movimento pode ser considerado em partes separadas, cada uma com sua própria aceleração constante.
RESOLUÇÃO DO DESLOCAMENTO (Δx) E DA POSIÇÃO FINAL (x) A PARTIR DA VELOCIDADE MÉDIA QUANDO A ACELERAÇÃO (a) É CONSTANTE
Para obter nossas duas primeiras novas equações, começamos com a definição de velocidade média:
\[\displaystyle \bar{v}=\frac{Δx}{Δt}\]
Substituindo a notação simplificada por\(\displaystyle Δx\) e\(\displaystyle Δt\) produz
Solução de\(\displaystyle x\) rendimentos
onde a velocidade média é
\[\displaystyle \bar{v}=\frac{v_0+v}{2} \label{eq5}\]
com constante\(a\).
A equação\ ref {eq5} reflete o fato de que, quando a aceleração\(v\) é constante, é apenas a média simples das velocidades inicial e final. Por exemplo, se você aumentar constantemente sua velocidade (ou seja, com aceleração constante) de 30 para 60 km/h, sua velocidade média durante esse aumento constante será de 45 km/h. Usando a equação\(\displaystyle \bar{v}=\frac{v_0+v}{2}\) para verificar isso, vemos que
\(\displaystyle \bar{v}=\frac{v_0+v}{2}=\frac{30 km/h+60 km/h}{2}=45 km/h,\)
o que parece lógico.
Exemplo\(\PageIndex{1}\): Calculating Displacement - How Far does the Jogger Run?
Um corredor corre por um trecho reto de estrada com uma velocidade média de 4,00 m/s por 2,00 min. Qual é sua posição final, considerando sua posição inicial zero?
Estratégia
Desenhe um esboço.
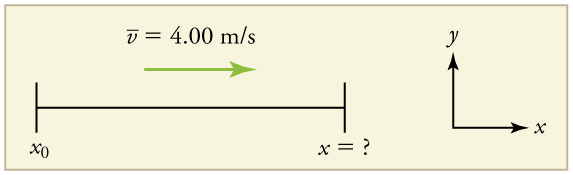
A posição final é dada pela equação
\(\displaystyle x=x_0+\bar{v}t\).
Para encontrar\(\displaystyle x\), identificamos os valores de\(\displaystyle x_0, \bar{v}\) e a\(\displaystyle t\) partir da declaração do problema e os substituímos na equação.
Solução
- Identifique os conhecidos. \(\displaystyle \bar{v}=4.00 m/s, Δt=2.00 min\),\(\displaystyle x_0=0 m\) e.
- Insira os valores conhecidos na equação.
Discussão
A velocidade e o deslocamento final são ambos positivos, o que significa que estão na mesma direção.
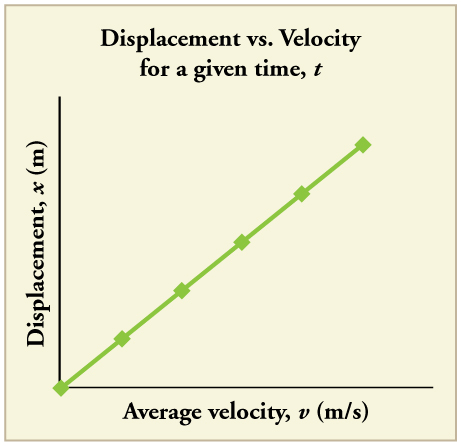
A equação\(\displaystyle x=x_0+\bar{v}t\) fornece uma visão sobre a relação entre deslocamento, velocidade média e tempo. Isso mostra, por exemplo, que o deslocamento é uma função linear da velocidade média. (Por função linear, queremos dizer que o deslocamento depende e\(\displaystyle \bar{v}\) não da\(\displaystyle \bar{v}\) elevação a alguma outra potência, como\(\displaystyle \bar{v}^2\). Quando representadas graficamente, as funções lineares parecem linhas retas com uma inclinação constante.) Em uma viagem de carro, por exemplo, chegaremos duas vezes mais longe em um determinado tempo se tivermos uma média de 90 km/h do que se tivermos uma média de 45 km/h.
RESOLUÇÃO DA VELOCIDADE FINAL
Podemos derivar outra equação útil manipulando a definição de aceleração.
\(\displaystyle a=\frac{Δv}{Δt}\)
Substituindo a notação simplificada por\(\displaystyle Δv\) e nos\(\displaystyle Δt\) dá
\[\displaystyle a=\frac{v−v_0}{t}\](constante a).
Solução de\(\displaystyle v\) rendimentos
\[\displaystyle v=v_0+at\](constantes).
Exemplo\(\PageIndex{2}\):Calculating Final Velocity: An Airplane Slowing Down after Landing
Um avião pousa com uma velocidade inicial de 70,0 m/s e depois desacelera\(\displaystyle 1.50 m/s^2\) por 40,0 s. Qual é sua velocidade final?
Estratégia
Desenhe um esboço. Desenhamos o vetor de aceleração na direção oposta ao vetor de velocidade porque o plano está desacelerando.
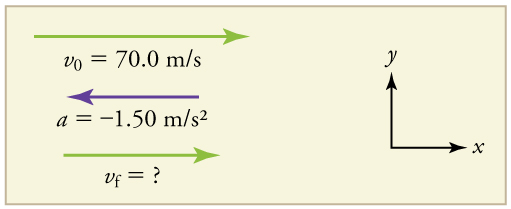
Solução
1. Identifique os conhecidos. \(\displaystyle v_0=70.0 m/s, a=−1.50 m/s^2, t=40.0s.\)
2. Identifique o desconhecido. Nesse caso, é a velocidade final,\(\displaystyle v_f\).
3. Determine qual equação usar. Podemos calcular a velocidade final usando a equação\(\displaystyle v=v_0+at\).
4. Insira os valores conhecidos e resolva.
\(\displaystyle v=v_0+at=70.0 m/s+(−1.50 m/s^2)(40.0 s)=10.0 m/s\)
Discussão
A velocidade final é muito menor que a velocidade inicial, conforme desejado ao diminuir a velocidade, mas ainda é positiva. Com motores a jato, o empuxo reverso pode ser mantido por tempo suficiente para parar o avião e começar a movê-lo para trás. Isso seria indicado por uma velocidade final negativa, o que não é o caso aqui.

Além de ser útil na resolução de problemas, a equação nos\(\displaystyle v=v_0+at\) dá uma visão das relações entre velocidade, aceleração e tempo. A partir daí, podemos ver, por exemplo, que
- a velocidade final depende de quão grande é a aceleração e quanto tempo ela dura
- se a aceleração for zero, a velocidade final será igual à velocidade inicial (\(\displaystyle v=v_0\)), conforme esperado (ou seja, a velocidade é constante)
- se a for negativo, então a velocidade final é menor que a velocidade inicial
(Todas essas observações se encaixam em nossa intuição e é sempre útil examinar equações básicas à luz de nossa intuição e experiências para verificar se elas realmente descrevem a natureza com precisão.)
FAZENDO CONEXÕES: CONEXÃO DO MUNDO REAL

Um míssil balístico intercontinental (ICBM) tem uma aceleração média maior do que o ônibus espacial e atinge uma velocidade maior no primeiro ou dois minutos de voo (os tempos reais de queima do ICBM são classificados - mísseis de curto tempo de queima são mais difíceis de serem destruídos por um inimigo). Mas o ônibus espacial obtém uma velocidade final maior, para que possa orbitar a Terra em vez de voltar diretamente para baixo, como faz um ICBM. O ônibus espacial faz isso acelerando por mais tempo.
RESOLUÇÃO DA POSIÇÃO FINAL QUANDO A VELOCIDADE NÃO É CONSTANTE (a≠ 0)
Podemos combinar as equações acima para encontrar uma terceira equação que nos permite calcular a posição final de um objeto em constante aceleração. Começamos com
\(\displaystyle v=v_0+at.\)
Somando\(\displaystyle v_0\) a cada lado dessa equação e dividindo por 2, obtém-se
\(\displaystyle \frac{v_0+v}{2}=v_0+\frac{1}{2}at\).
Como\\ frac {(v_0+v} {2} =\ bar {v}\) para aceleração constante, então
\(\displaystyle \bar{v}=v_0+\frac{1}{2}at\).
Agora substituímos essa expressão por\(\displaystyle \bar{v}\) na equação para deslocamento\(\displaystyle x=x_0+\bar{v}t\), produzindo
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)(constante a).
Exemplo\(\PageIndex{3}\): Calculating Displacement of an Accelerating Object - Dragsters
Os dragsters podem atingir acelerações médias de\(\displaystyle 26.0 m/s^2\). Suppose such a dragster accelerates from rest at this rate for 5.56 s. How far does it travel in this time?

Estratégia
Desenhe um esboço.
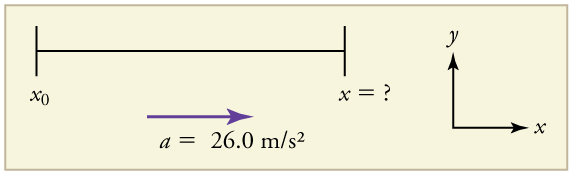
Somos convidados a encontrar o deslocamento, que é\(\displaystyle x\) if we take \(\displaystyle x_0\) to be zero. (Think about it like the starting line of a race. It can be anywhere, but we call it 0 and measure all other positions relative to it.) We can use the equation \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) once we identify \(\displaystyle v_0, a,\) and \(\displaystyle t\) from the statement of the problem.
Solução
1. Identifique os conhecidos. Começar do descanso significa que\(\displaystyle v_0=0, a\) is given as \(\displaystyle 26.0m/s^2\) and t is given as 5.56 s.
2. Insira os valores conhecidos na equação para resolver o x desconhecido:
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\).
Como a posição inicial e a velocidade são ambas zero, isso simplifica para
\(\displaystyle x=\frac{1}{2}at^2\).
Substituindo os valores identificados de a e t dá
\(\displaystyle x=\frac{1}{2}(26.0 m/s^2)(5.56 s)^2\),
produzindo
\(\displaystyle x=402 m.\)
Discussão
Se convertermos 402 m em milhas, descobrimos que a distância percorrida é muito próxima de um quarto de milha, a distância padrão para corridas de arrancada. Portanto, a resposta é razoável. Este é um deslocamento impressionante em apenas 5,56 s, mas dragsters de alto nível podem fazer um quarto de milha em ainda menos tempo do que isso.
O que mais podemos aprender examinando a equação\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)? Nós vemos isso:
- o deslocamento depende do quadrado do tempo decorrido quando a aceleração não é zero. No exemplo, o dragster cobre apenas um quarto da distância total na primeira metade do tempo decorrido
- se a aceleração for zero, então a velocidade inicial é igual à velocidade média (\(\displaystyle v_0=\bar{v}\)) e\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) se torna\(\displaystyle x=x_0+v_0t\)
RESOLUÇÃO DA VELOCIDADE FINAL QUANDO A VELOCIDADE NÃO É CONSTANTE (a≠ 0)
Uma quarta equação útil pode ser obtida a partir de outra manipulação algébrica de equações anteriores.
Se\(\displaystyle v=v_0+at\) resolvermos\(\displaystyle t\), obtemos
\(\displaystyle t=\frac{v−v_0}{a}\).
Substituindo isso e\(\displaystyle \bar{v}=\frac{v_0+v}{2}\) em\(\displaystyle x=x_0+\bar{v}t\), obtemos
\(\displaystyle v^2=v^2_0+2a(x−x_0)\)(constante a).
Exemplo\(\PageIndex{4}\): Calculating Final Velocity: Dragsters
Calcule a velocidade final do dragster no Example\(\PageIndex{3}\) sem usar informações sobre o tempo.
Estratégia
Desenhe um esboço.
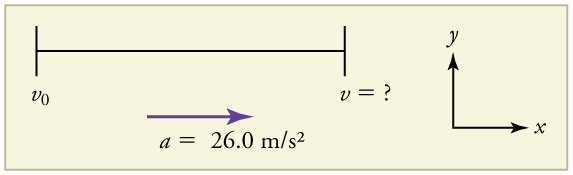
A equação\(\displaystyle v^2=v^2_0+2a(x−x_0)\) é ideal para essa tarefa porque relaciona velocidades, aceleração e deslocamento, e nenhuma informação de tempo é necessária.
Solução
1. Identifique os valores conhecidos. Sabemos disso\(\displaystyle v_0=0\), já que o dragster começa do repouso. Em seguida, notamos isso\(\displaystyle x−x_0=402 m\) (essa foi a resposta no Exemplo). Finalmente, a aceleração média foi dada para ser\(\displaystyle a=26.0 m/s^2\).
2. Conecte os conhecidos na equação\(\displaystyle v^2=v^2_0+2a(x−x_0)\) e resolva por\(\displaystyle v\).
\(\displaystyle v^2=0+2(26.0 m/s^2)(402 m).\)
Assim
\(\displaystyle v^2=2.09×10^4m^2/s^2.\)
Para obter\(\displaystyle v\), pegamos a raiz quadrada:
\(\displaystyle v=\sqrt{2.09×10^4m^2/s^2}=145 m/s\).
Discussão
145 m/s é de cerca de 522 km/h ou cerca de 324 mi/h, mas mesmo essa velocidade vertiginosa está aquém do recorde de um quarto de milha. Além disso, observe que uma raiz quadrada tem dois valores; usamos o valor positivo para indicar uma velocidade na mesma direção da aceleração.
Um exame da equação\(\displaystyle v^2=v^2_0+2a(x−x_0)\) pode produzir mais informações sobre as relações gerais entre quantidades físicas:
- A velocidade final depende do tamanho da aceleração e da distância sobre a qual ela atua
- Para uma desaceleração fixa, um carro que está indo duas vezes mais rápido não para simplesmente no dobro da distância — ele leva muito mais tempo para parar. (É por isso que reduzimos as zonas de velocidade perto das escolas.)
Juntando equações
Nos exemplos a seguir, exploramos ainda mais o movimento unidimensional, mas em situações que exigem um pouco mais de manipulação algébrica. Os exemplos também fornecem informações sobre técnicas de resolução de problemas. A caixa abaixo fornece uma referência fácil às equações necessárias.
RESUMO DAS EQUAÇÕES CINEMÁTICAS (CONSTANTE a)
\(\displaystyle x=x_0+\bar{v}t\)
\(\displaystyle \bar{v}=\frac{v_0+v}{2}\)
\(\displaystyle v=v_0+at\)
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle v^2=v^2_0+2a(x−x_0)\)
Exemplo\(\PageIndex{5}\):Calculating Displacement: How Far Does a Car Go When Coming to a Halt?
Em concreto seco, um carro pode desacelerar a uma taxa de\(7.00 m/s^2\), enquanto no concreto úmido ele pode desacelerar apenas\(5.00 m/s^2\). Encontre as distâncias necessárias para parar um carro em movimento a 30,0 m/s (cerca de 110 km/h)
- em concreto seco e
- em concreto molhado.
- Repita os dois cálculos, encontrando o deslocamento a partir do ponto em que o motorista vê um semáforo ficar vermelho, levando em consideração seu tempo de reação de 0,500 s para colocar o pé no freio.
Estratégia
Desenhe um esboço.

Para determinar quais equações são melhores para usar, precisamos listar todos os valores conhecidos e identificar exatamente o que precisamos resolver. Faremos isso explicitamente nos próximos exemplos, usando tabelas para defini-los.
Solução para (a)
1. Identifique os conhecidos e o que queremos resolver. Sabemos disso\(\displaystyle v_0=30.0 m/s; v=0; a=−7.00m/s^2\) (\(\displaystyle a\)é negativo porque está em uma direção oposta à velocidade). Nós\(\displaystyle x_0\) consideramos ser\(\displaystyle 0\). Estamos procurando por deslocamento\(\displaystyle Δx\), ou\(\displaystyle x−x_0\).
2. Identifique a equação que ajudará a resolver o problema. A melhor equação a ser usada é
\(\displaystyle v^2=v^2_0+2a(x−x_0)\).
Essa equação é melhor porque inclui apenas uma incógnita,\(\displaystyle x\). Conhecemos os valores de todas as outras variáveis nessa equação. (Existem outras equações que nos permitiriam resolver\(\displaystyle x\), mas elas exigem que saibamos o tempo de parada\(\displaystyle t\), que não conhecemos. Poderíamos usá-los, mas isso implicaria cálculos adicionais.)
3. Reorganize a equação para resolver\(\displaystyle x\).
\(\displaystyle x−x_0=\frac{v^2−v^2_0}{2a}\)
4. Insira valores conhecidos.
\(\displaystyle x−0=\frac{0^2−(30.0 m/s)^2}{2(−7.00 m/s^2)}\)
Assim,
\(\displaystyle x=64.3 m\)em concreto seco.
Solução para (b)
Esta parte pode ser resolvida exatamente da mesma maneira que a Parte A. A única diferença é que a desaceleração é\(\displaystyle –5.00 m/s^2\). O resultado é
\(\displaystyle x_{wet}=90.0 m\)em concreto molhado.
Solução para (c)
Uma vez que o motorista reage, a distância de parada é a mesma das Partes A e B para concreto seco e úmido. Então, para responder a essa pergunta, precisamos calcular a distância que o carro percorre durante o tempo de reação e, em seguida, adicionar isso ao tempo de parada. É razoável supor que a velocidade permaneça constante durante o tempo de reação do motorista.
1. Identifique os conhecidos e o que queremos resolver. Nós sabemos disso\(\displaystyle \bar{v}=30.0 m/s; t_{reaction}=0.500s; a_{reaction}=0\). Nós\(\displaystyle x_{0−reaction}\) consideramos 0. Estamos procurando\(\displaystyle x_{reaction}\).
2. Identifique a melhor equação a ser usada.
\(\displaystyle x=x_0+\bar{v}t\)funciona bem porque o único valor desconhecido é\(\displaystyle x\), que é o que queremos resolver.
3. Conecte os conhecidos para resolver a equação.
\(\displaystyle x=0+(30.0 m/s)(0.500 s)=15.0 m.\)
Isso significa que o carro viaja 15,0 m enquanto o motorista reage, fazendo com que os deslocamentos totais nos dois casos de concreto seco e úmido sejam 15,0 m maiores do que se ele reagisse instantaneamente.
4. Adicione o deslocamento durante o tempo de reação ao deslocamento durante a frenagem.
\(\displaystyle x_{braking}+x_{reaction}=x_{total}\)
a. 64,3 m + 15,0 m = 79,3 m quando seco
b. 90,0 m + 15,0 m = 105 m quando molhado
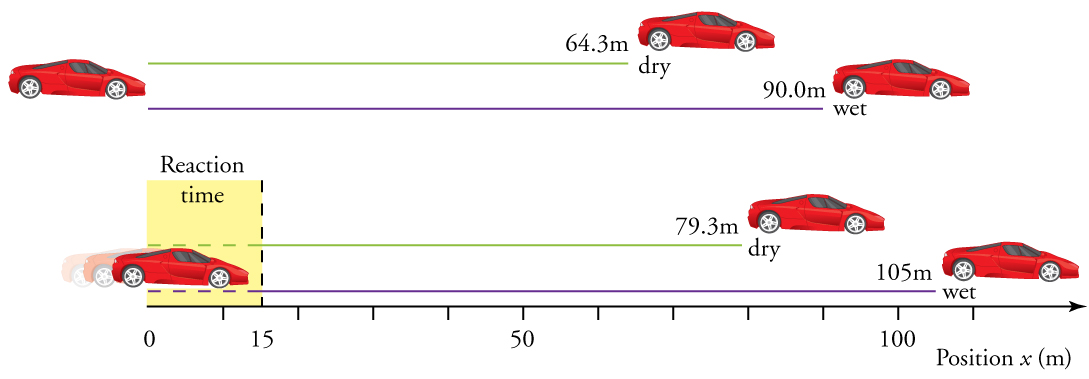
Discussão
Os deslocamentos encontrados neste exemplo parecem razoáveis para parar um carro em movimento rápido. Deve levar mais tempo para parar um carro em piso molhado em vez de seco. É interessante que o tempo de reação aumente significativamente os deslocamentos. Mas o mais importante é a abordagem geral para resolver problemas. Identificamos os conhecidos e as quantidades a serem determinadas e, em seguida, encontramos uma equação apropriada. Muitas vezes, há mais de uma maneira de resolver um problema. As várias partes deste exemplo podem, de fato, ser resolvidas por outros métodos, mas as soluções apresentadas acima são as mais curtas.
Exemplo\(\PageIndex{5}\): Calculating Time - A Car Merges into Traffic
Suponha que um carro se junte ao tráfego da rodovia em uma rampa de 200 m de comprimento. Se sua velocidade inicial é de 10,0 m/s e acelera a\(\displaystyle .00 m/s^2\), quanto tempo é necessário para percorrer os 200 m até a rampa? (Essas informações podem ser úteis para um engenheiro de tráfego.)
Estratégia
Desenhe um esboço.
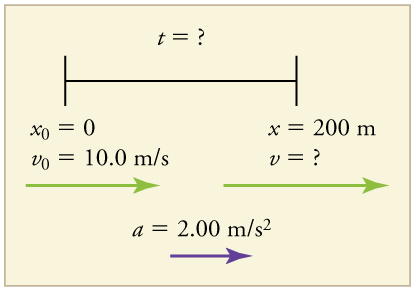
Solução
1. Identifique os conhecidos e o que queremos resolver. Nós sabemos disso\(\displaystyle v_0=10 m/s; a=2.00 m/s^2\); and \(\displaystyle x=200 m.\)
2. Precisamos resolver para t. Escolha a melhor equação. \(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\) works best because the only unknown in the equation is the variable t for which we need to solve.
3. Precisaremos reorganizar a equação para resolver\(t\). In this case, it will be easier to plug in the knowns first.
\(\displaystyle 200 m=0 m+(10.0 m/s)t+\frac{1}{2}(2.00 m/s^2)t^2\)
4. Simplifique a equação. As unidades de metros (m) são canceladas porque estão em cada período. Podemos obter as unidades de segundo (s) para cancelar tomando\(\displaystyle t=ts\), where \(\displaystyle t\) is the magnitude of time and s is the unit. Doing so leaves
\(\displaystyle 200=10t+t^2.\)
5. Use a fórmula quadrática para resolver\(\displaystyle t\).
(a) Reorganize a equação para obter 0 em um lado da equação.
\(\displaystyle t^2+10t−200=0\)
Esta é uma equação quadrática da forma
\(\displaystyle at^2+bt+c=0,\)
onde estão as constantes\(\displaystyle a=1.00,b=10.0\),and \(\displaystyle c=−200.\)
(b) Suas soluções são dadas pela fórmula quadrática:
\(\displaystyle t=\frac{−b±\sqrt{b^2−4ac}}{2a}\).
Isso gera duas soluções para\(\displaystyle t\), which are
\(\displaystyle t=10.0\) and \(\displaystyle −20.0\).
Nesse caso, então, o tempo é\(\displaystyle t=t\) in seconds, or
\(\displaystyle t=10.0s\) and \(\displaystyle −20.0s\).
Um valor negativo para o tempo não é razoável, pois isso significaria que o evento aconteceu 20 s antes do início da moção. Podemos descartar essa solução. Assim,
\(\displaystyle t=10.0s.\)
Discussão
Sempre que uma equação contém um quadrado desconhecido, haverá duas soluções. Em alguns problemas, ambas as soluções são significativas, mas em outros, como os acima, apenas uma solução é razoável. A resposta de 10.0 s parece razoável para uma rampa de acesso típica de uma rodovia.
Com o básico da cinemática estabelecido, podemos continuar com muitos outros exemplos e aplicações interessantes. No processo de desenvolvimento da cinemática, também vislumbramos uma abordagem geral para a resolução de problemas que produz respostas corretas e insights sobre relacionamentos físicos. Princípios básicos da solução de problemas discute os princípios básicos da solução de problemas e descreve uma abordagem que o ajudará a ter sucesso nessa tarefa inestimável.
FAZENDO CONEXÕES: EXPERIMENTO PARA LEVAR PARA CASA — NOTÍCIAS DE ÚLTIMA HORA
Estamos usando unidades SI de metros quadrados por segundo para descrever alguns exemplos de aceleração ou desaceleração de carros, corredores e trens. Para ter uma ideia melhor desses números, pode-se medir a desaceleração da frenagem de um carro fazendo uma parada lenta (e segura). Lembre-se de que, para aceleração média,\(\displaystyle \bar{a}=Δv/Δt\). Ao viajar em um carro, aplique lentamente os freios ao chegar a um sinal de pare. Peça a um passageiro que anote a velocidade inicial em milhas por hora e o tempo gasto (em segundos) para parar. A partir disso, calcule a desaceleração em milhas por hora por segundo. Converta isso em metros por segundo quadrado e compare com outras desacelerações mencionadas neste capítulo. Calcule a distância percorrida na frenagem.
Exercício\(\PageIndex{1}\)
Um foguete tripulado acelera a uma taxa de\(\displaystyle 20 m/s^2\) durante o lançamento. Quanto tempo o foguete leva para atingir a velocidade de 400 m/s?
- Resposta
-
Para responder a isso, escolha uma equação que permita resolver por tempo\(\displaystyle t\)\(\displaystyle a, v_0\), considerando apenas\(\displaystyle v\) e.
\(\displaystyle v=v_0+at\)
Reorganize para resolver\(\displaystyle t\).
\(\displaystyle t=\frac{v−v_0}{a}=\frac{400 m/s−0 m/s}{20 m/s^2}=20 s\)
Resumo
- Para simplificar os cálculos, consideramos que a aceleração é constante, de modo que\(\displaystyle \bar{a}=a\) em todos os momentos.
- Também consideramos que o tempo inicial é zero.
- A posição inicial e a velocidade recebem um subscrito 0; os valores finais não têm subscrito. Assim,
\(\displaystyle Δt=t\)
\(\displaystyle Δx=x−x_0\)
\(\displaystyle Δv=v−v_0\)
- As seguintes equações cinemáticas para movimento com constante a são úteis:
\(\displaystyle x=x_0+\bar{v}t\)
\(\displaystyle \bar{v}=\frac{v_0+v}{2}\)
\(\displaystyle v=v_0+at\)
\(\displaystyle x=x_0+v_0t+\frac{1}{2}at^2\)
\(\displaystyle v^2=v^2_0+2a(x−x_0)\)
- Em movimento vertical,\(\displaystyle y\) é substituído por\(\displaystyle x\).


