2.4: Aceleração

Last updated
Save as PDF

Page ID: 194255

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de

Ao final desta seção, você poderá:

Defina e faça a distinção entre aceleração instantânea, aceleração média e desaceleração.
Calcule a aceleração com base no tempo inicial, na velocidade inicial, no tempo final e na velocidade final.

Na conversa cotidiana, acelerar significa acelerar. O acelerador de um carro pode, de fato, fazer com que ele acelere. Quanto maior a aceleração, maior a mudança na velocidade em um determinado período. A definição formal de aceleração é consistente com essas noções, mas mais inclusiva.

Figura\(\PageIndex{1}\): Um avião desacelera ou desacelera quando chega para pousar em St. Maarten. Sua aceleração é oposta em direção à sua velocidade. (crédito: Steve Conry, Flickr)

Definição: Aceleração média

A aceleração média é a taxa na qual a velocidade muda,

\[\bar{a}=\frac{Δv}{Δt}=\frac{v_f−v_0}{t_f−t_0}\]

onde\(\bar{a}\) é a aceleração média,\(v\) é a velocidade e\( t\) é o tempo. (A barra acima\(a\) da média.)

Como aceleração é a velocidade em m/s dividida pelo tempo em s, as unidades SI para aceleração são\( m/s^2\), metros por segundo quadrado ou metros por segundo por segundo por segundo, o que significa literalmente em quantos metros por segundo a velocidade muda a cada segundo.

Lembre-se de que a velocidade é um vetor — ela tem magnitude e direção. Isso significa que uma mudança na velocidade pode ser uma mudança na magnitude (ou velocidade), mas também pode ser uma mudança na direção. Por exemplo, se um carro vira uma curva em velocidade constante, ele está acelerando porque sua direção está mudando. Quanto mais rápido você virar, maior será a aceleração. Portanto, há uma aceleração quando a velocidade muda em magnitude (um aumento ou diminuição na velocidade) ou na direção, ou ambos.

ACELERAÇÃO COMO VETOR

A aceleração é um vetor na mesma direção da mudança na velocidade,\(Δv\). Como a velocidade é um vetor, ela pode mudar tanto em magnitude quanto em direção. A aceleração é, portanto, uma mudança na velocidade ou direção, ou em ambas.

Lembre-se de que, embora a aceleração esteja na direção da mudança na velocidade, ela nem sempre está na direção do movimento. Quando um objeto fica mais lento, sua aceleração é oposta à direção de seu movimento. Isso é conhecido como desaceleração.

Um trem do metrô chegando a uma estação. Uma seta vetorial de velocidade aponta ao longo da trilha para longe do trem. Uma seta vetorial de aceleração aponta ao longo da pista em direção ao trem. — Figura\(\PageIndex{2}\): Um trem do metrô em São Paulo, Brasil, desacelera ao entrar em uma estação. Ele está acelerando em uma direção oposta à direção de seu movimento. (crédito: Yusuke Kawasaki, Flickr)

ALERTA DE EQUÍVOCO: DESACELERAÇÃO VS. ACELERAÇÃO NEGATIVA

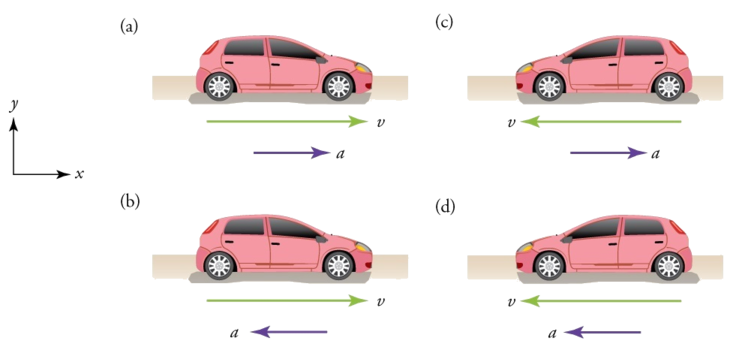
A desaceleração sempre se refere à aceleração na direção oposta à direção da velocidade. A desaceleração sempre reduz a velocidade. A aceleração negativa, entretanto, é a aceleração na direção negativa no sistema de coordenadas escolhido. A aceleração negativa pode ou não ser desaceleração, e a desaceleração pode ou não ser considerada aceleração negativa. Se a aceleração tiver o mesmo sinal da velocidade, o objeto está acelerando. Se a aceleração tiver o sinal oposto à velocidade, o objeto está diminuindo. Por exemplo, considere a Figura\(\PageIndex{2}\).

Quatro diagramas separados de carros em movimento. Diagrama a: Um carro se movendo para a direita. Uma seta vetorial de velocidade aponta para a direita. Uma seta vetorial de aceleração também aponta para a direita. Diagrama b: Um carro se movendo para a direita na direção x positiva. Uma seta vetorial de velocidade aponta para a direita. Uma seta vetorial de aceleração aponta para a esquerda. Diagrama c: Um carro se movendo para a esquerda. Uma seta vetorial de velocidade aponta para a esquerda. Uma seta vetorial de aceleração aponta para a direita. Diagrama d: Um carro se movendo para a esquerda. Uma seta vetorial de velocidade aponta para a esquerda. Uma seta vetorial de aceleração também aponta para a esquerda. — Figura\(\PageIndex{3}\): (a) Este carro está acelerando à medida que se move para a direita. Portanto, tem aceleração positiva em nosso sistema de coordenadas. (b) Este carro está diminuindo a velocidade à medida que se move para a direita. Portanto, ele tem aceleração negativa em nosso sistema de coordenadas, porque sua aceleração é para a esquerda. O carro também está desacelerando: a direção de sua aceleração é oposta à direção do movimento. (c) Este carro está se movendo para a esquerda, mas diminuindo a velocidade com o tempo. Portanto, sua aceleração é positiva em nosso sistema de coordenadas porque está voltada para a direita. No entanto, o carro está desacelerando porque sua aceleração é oposta ao seu movimento. (d) Este carro está acelerando à medida que se move para a esquerda. Tem aceleração negativa porque está acelerando para a esquerda. No entanto, como sua aceleração está na mesma direção de seu movimento, ela está acelerando (não desacelerando).

Exemplo\(\PageIndex{1}\): Calculating Acceleration: A Racehorse Leaves the Gate

Um cavalo de corrida saindo do portão acelera do repouso até uma velocidade de 15,0 m/s para oeste em 1,80 s. Qual é sua aceleração média?

Figura\(\PageIndex{4}\): Dois cavalos de corrida correndo para a esquerda. (crédito: Jon Sullivan, PD Photo.org)

Estratégia

Primeiro, desenhamos um esboço e atribuímos um sistema de coordenadas ao problema. Esse é um problema simples, mas sempre ajuda visualizá-lo. Observe que atribuímos leste como positivo e oeste como negativo. Assim, nesse caso, temos velocidade negativa.

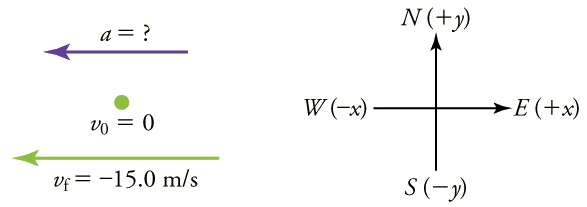
Uma seta vetorial de aceleração apontando para o oeste, na direção x negativa, rotulada com um ponto de interrogação igual. Uma seta vetorial de velocidade também apontando para a esquerda, com a velocidade inicial rotulada como 0 e a velocidade final rotulada como menos quinze pontos 0 metros por segundo. — Figura\(\PageIndex{5}\).

Podemos resolver esse problema identificando\(Δv\) e a\(Δt\) partir das informações fornecidas e, em seguida, calculando a aceleração média diretamente da Equação\ ref {averagea}:

\[\bar{a}=\dfrac{Δv}{Δt}=\dfrac{v_f−v_0}{t_f−t_0}. \nonumber\]

Solução

Identifique os conhecidos. \(v_0=0 , v_f=−15.0 m/s\)(o sinal negativo indica direção para o oeste),\( Δt=1.80 s\).
Encontre a mudança na velocidade. Como o cavalo está indo de zero para\( −15.0 m/s\), sua mudança na velocidade é igual à velocidade final:\[Δv=v_f=−15.0\, m/s .\nonumber\]
Insira os valores conhecidos (\(Δv\)e\(Δt\)) e resolva o desconhecido\(\bar{a}\).

\(\bar{a}=\frac{Δv}{Δt}=\frac{−15.0 m/s}{1.80 s}=−8.33 m/s^2\).

Discussão

O sinal negativo de aceleração indica que a aceleração está voltada para o oeste. Uma aceleração do\(8.33\, m/s^2\) oeste significa que o cavalo aumenta sua velocidade em 8,33 m/s para oeste a cada segundo, ou seja, 8,33 metros por segundo por segundo, como escrevemos\( 8.33\, m/s^2\). Esta é realmente uma aceleração média, porque a viagem não é suave. Veremos mais tarde que uma aceleração dessa magnitude exigiria que o piloto aguentasse com uma força quase igual ao seu peso.

Aceleração instantânea

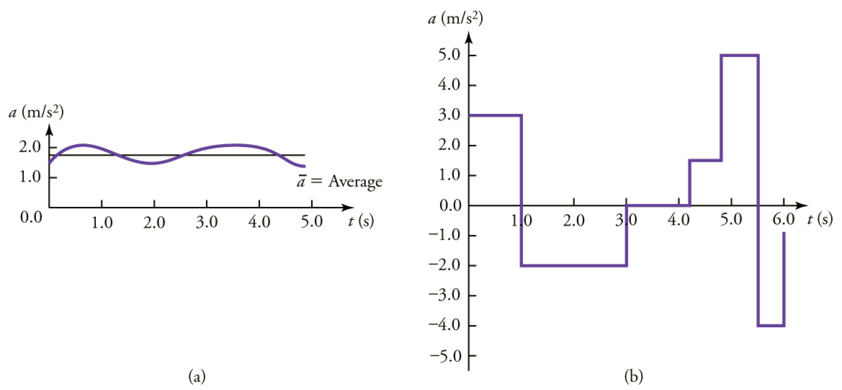
A aceleração instantânea\( a\), ou a aceleração em um instante específico no tempo, é obtida pelo mesmo processo discutido para a velocidade instantânea em Tempo, Velocidade e Velocidade, ou seja, considerando um intervalo de tempo infinitesimalmente pequeno. Como podemos encontrar a aceleração instantânea usando apenas álgebra? A resposta é que escolhemos uma aceleração média que seja representativa do movimento. A figura\(\PageIndex{6}\) mostra gráficos de aceleração instantânea versus tempo para dois movimentos muito diferentes. Na Figura\(\PageIndex{6a}\), a aceleração varia um pouco e a média em todo o intervalo é quase a mesma da aceleração instantânea a qualquer momento. Nesse caso, devemos tratar esse movimento como se ele tivesse uma aceleração constante igual à média (neste caso, cerca de\(1.8 m/s^2\)). Na Figura\(\PageIndex{6b}\), a aceleração varia drasticamente ao longo do tempo. Em tais situações, é melhor considerar intervalos de tempo menores e escolher uma aceleração média para cada um. Por exemplo, podemos considerar o movimento nos intervalos de tempo de 0 a 1,0 s e de 1,0 a 3,0 s como movimentos separados com acelerações de\( +3.0\, m/s^2\) e\( –2.0 \,m/s^2\), respectivamente.

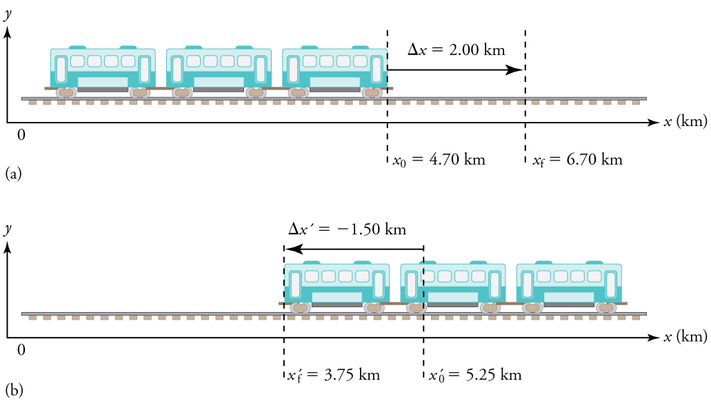
Os próximos exemplos consideram o movimento do trem do metrô mostrado na Figura\(\PageIndex{7}\). Na Figura,\(\PageIndex{7a}\) a peteca se move para a direita e, na Figura,\(\PageIndex{7b}\) ela se move para a esquerda. Os exemplos são projetados para ilustrar ainda mais aspectos do movimento e ilustrar alguns dos raciocínios necessários para resolver problemas.

Na parte (a), um trem do metrô se move da esquerda para a direita de uma posição inicial de x igual a 4 ponto 7 quilômetros até uma posição final de x igual a 6 ponto 7 quilômetros, com um deslocamento de 2 ponto 0 quilômetros. Na parte (b), o trem se move para a esquerda, de uma posição inicial de 5 pontos 25 quilômetros para uma posição final de 3 pontos 75 quilômetros. — Figura\(\PageIndex{7}\): Movimento unidimensional de um trem do metrô considerado em Exemplos\(\PageIndex{2}\) -\(\PageIndex{5}\). Aqui, escolhemos o eixo x para que + signifique à direita e − signifique à esquerda para deslocamentos, velocidades e acelerações. (a) O trem do metrô se move para a direita de\(x_0\) para\(x_f\). Seu deslocamento\(Δx\) é de +2,0 km. (b) O trem se move para a esquerda de\(x_0\) para\(x_f\). Seu deslocamento\(Δx\) é\(−1.5 km\). (Note que o símbolo primo (′) é usado simplesmente para distinguir entre deslocamentos em duas situações diferentes. As distâncias de viagem e o tamanho dos carros estão em escalas diferentes para caber tudo no diagrama.)

Exemplo\(\PageIndex{2}\): Calculating Displacement - A Subway Train

Quais são a magnitude e o sinal dos deslocamentos dos movimentos do metrô mostrados nas partes (a) e (b) da Figura\(\PageIndex{7}\)?

Estratégia

Um desenho com um sistema de coordenadas já foi fornecido, então não precisamos fazer um esboço, mas devemos analisá-lo para ter certeza de que entendemos o que ele está mostrando. Preste atenção especial ao sistema de coordenadas. Para encontrar o deslocamento, usamos a equação\( Δx=x_f−x_0\). Isso é simples, pois as posições inicial e final são fornecidas.

Solução

Identifique os conhecidos. Na figura vemos isso\(x_f=6.70\, km \) e\(x_0=4.70\, km\) para a parte (a)\(x'_f=3.75\, km \) e\(x'_0=5.25\, km \) para a parte (b).
Resolva o deslocamento na parte (a). \[\begin{align*} Δx &=x_f−x_0 \\[5pt] &=6.70\, km−4.70\, km \\[5pt] &=+2.00 \,km \end{align*}\]
Resolva o deslocamento na parte (b). \[\begin{align*} Δx' &=x'_f−x'_0 \\[5pt] &=3.75\, km−5.25\, km \\[5pt] &=−1.50\, km \end{align*}\]

Discussão

A direção do movimento em (a) é para a direita e, portanto, seu deslocamento tem um sinal positivo, enquanto o movimento em (b) é para a esquerda e, portanto, tem um sinal negativo.

Exemplo\(\PageIndex{3}\): Comparing Distance Traveled with Displacement - A Subway Train

Quais são as distâncias percorridas para os movimentos mostrados nas partes (a) e (b) do trem do metrô na Figura\(\PageIndex{7}\)?

Estratégia

Para responder a essa pergunta, pense nas definições de distância e distância percorrida e como elas estão relacionadas ao deslocamento. A distância entre duas posições é definida como a magnitude do deslocamento, que foi encontrada em Example\(\PageIndex{2}\). A distância percorrida é o comprimento total do caminho percorrido entre as duas posições (consulte a Seção sobre Deslocamento). No caso do trem do metrô mostrado na Figura\(\PageIndex{7}\), a distância percorrida é a mesma que a distância entre as posições inicial e final do trem.

Solução

1. O deslocamento da parte (a) foi de +2,00 km. Portanto, a distância entre as posições inicial e final foi de 2,00 km e a distância percorrida foi de 2,00 km.

2. O deslocamento da peça (b) foi\( −1.5 km\). Portanto, a distância entre as posições inicial e final foi de 1,50 km e a distância percorrida foi de 1,50 km.

Discussão

A distância é um escalar. Tem magnitude, mas nenhum sinal que indique a direção.

Exemplo\(\PageIndex{4}\): Calculating Acceleration: A Subway Train Speeding Up

Suponha que o trem na Figura\(\PageIndex{7a}\) acelere do repouso para 30,0 km/h nos primeiros 20,0 s de seu movimento. Qual é a aceleração média durante esse intervalo de tempo?

Estratégia

Neste momento, vale a pena fazer um esboço simples:

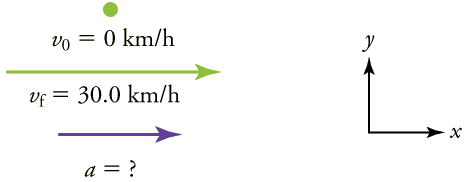
Um ponto representa a velocidade inicial de 0 quilômetros por segundo. Abaixo do ponto está uma seta vetorial de velocidade apontando para a direita, representando a velocidade final de trinta pontos zero quilômetros por hora. Abaixo do vetor de velocidade, há uma seta vetorial de aceleração rotulada como ponto de interrogação igual. — Figura\(\PageIndex{8}\): Esse problema envolve três etapas. Primeiro, devemos determinar a mudança na velocidade, depois devemos determinar a mudança no tempo e, finalmente, usar esses valores para calcular a aceleração.

Solução

Identifique os conhecidos. \( v_0=0\)(os trens partem em repouso)\( v_f=30.0 km/h \),,\(Δt=20.0 s \) e.
Calcule\(Δv\). Como o trem parte do repouso, sua mudança de velocidade é\(Δv=+30.0 km/h \), onde o sinal de mais significa velocidade para a direita.
Insira valores conhecidos e resolva o desconhecido,\(\bar{ a}\). \[\bar{a}=\dfrac{Δv}{Δt}=\dfrac{+30.0 km/h}{20.0 s}\nonumber\]
Como as unidades são misturadas (temos horas e segundos de tempo), precisamos converter tudo em unidades SI de metros e segundos. (Consulte Quantidades e Unidades Físicas para obter mais orientações.) \[\bar{a}=\left(\dfrac{+30 km/h}{20.0 s}\right)\left(\dfrac{10^3m}{1 km}\right)\left(\dfrac{1h}{3600 s}\right)=0.417 m/s^2 \nonumber\]

Discussão

O sinal de mais significa que a aceleração está à direita. Isso é razoável porque o trem parte do repouso e acaba com uma velocidade para a direita (também positiva). Portanto, a aceleração está na mesma direção da mudança de velocidade, como sempre acontece.

Exemplo\(\PageIndex{5}\): Calculate Acceleration

Um trem do metrô está desacelerando: Agora, suponha que, no final de sua viagem, o trem na Figura\(\PageIndex{7a}\) desacelere até parar a uma velocidade de 30,0 km/h em 8,00 s. Qual é a aceleração média ao parar?

Estratégia

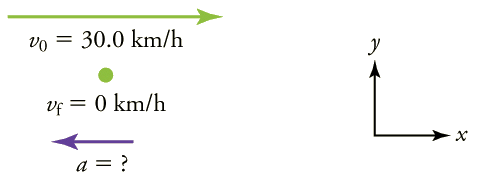
Uma seta vetorial de velocidade apontando para a direita com velocidade inicial de trinta pontos zero quilômetros por hora e velocidade final de 0. Uma seta vetorial de aceleração apontando para a esquerda, rotulada como ponto de interrogação igual. — Figura\(\PageIndex{9}\):.

Nesse caso, o trem está desacelerando e sua aceleração é negativa porque está voltada para a esquerda. Como no exemplo anterior, devemos encontrar a mudança na velocidade e a mudança no tempo e, em seguida, resolver a aceleração.

Solução

Identifique os conhecidos. \(v_0=30.0 km/h , v_f=0 km/h\)(o trem está parado, então sua velocidade é 0),\(Δt=8.00 s \) e.
Resolva a mudança na velocidade,\(Δv\). \[Δv=v_f−v_0=0−30.0 km/h=−30.0 km/h \nonumber\]
Conecte os conhecidos\( Δv\) e\(Δt\) resolva por\(\bar{a}\). \[\bar{a}=\dfrac{Δv}{Δt}=\dfrac{−30.0 km/h}{8.00 s} \nonumber\]
Converta as unidades em metros e segundos. \[\bar{a}=\dfrac{Δv}{Δt}=\left(\dfrac{−30.0 km/h}{8.00 s}\right)\left(\dfrac{10^3m}{1 km}\right)\left(\dfrac{1 h}{3600 s}\right)=−1.04 m/s^2. \nonumber\]

Discussão

O sinal de menos indica que a aceleração está à esquerda. Esse sinal é razoável porque o trem inicialmente tem uma velocidade positiva nesse problema, e uma aceleração negativa se oporia ao movimento. Novamente, a aceleração está na mesma direção da mudança na velocidade, que é negativa aqui. Essa aceleração pode ser chamada de desaceleração porque tem uma direção oposta à velocidade.

Os gráficos de posição, velocidade e aceleração versus tempo dos trens em Exemplo\(\PageIndex{4}\) e\(\PageIndex{5}\) são exibidos na Figura\(\PageIndex{10}\). (Consideramos que a velocidade permanece constante de 20 a 40 s, após o qual o trem desacelera.)

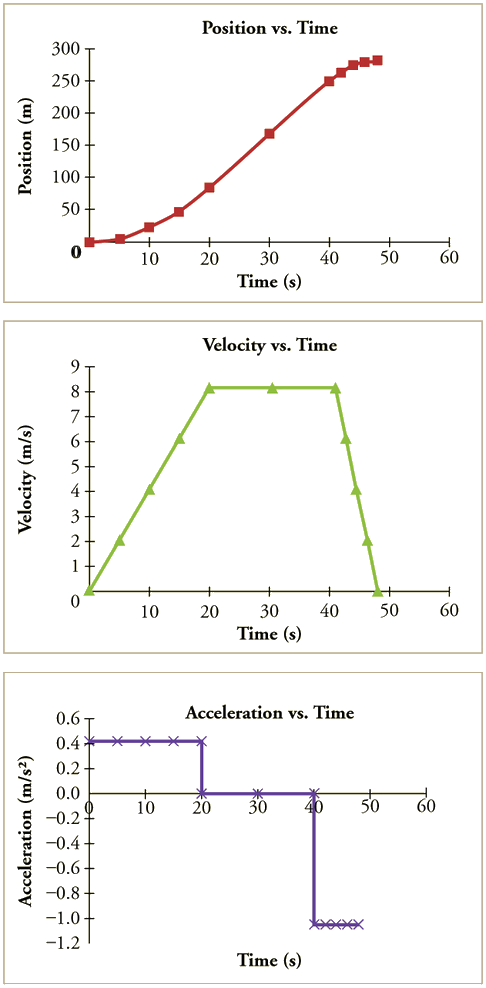
Três gráficos. O primeiro é um gráfico linear da posição em metros versus o tempo em segundos. A linha começa na origem e tem uma forma côncava, desde o tempo igual a zero até o tempo igual a vinte segundos. É reto com uma inclinação positiva de vinte segundos a quarenta segundos. Em seguida, é convexo de quarenta a cinquenta segundos. O segundo gráfico é um gráfico linear da velocidade em metros por segundo versus tempo em segundos. A linha é reta com uma inclinação positiva começando na origem de 0 a vinte segundos. É plano de vinte a quarenta segundos. De quarenta a cinquenta segundos, a linha é reta com uma inclinação negativa de volta para uma velocidade de 0. O terceiro gráfico é um gráfico linear de aceleração em metros por segundo por segundo versus tempo em segundos. A linha é plana com uma aceleração positiva constante de zero a vinte segundos. A linha então cai para uma aceleração de 0 de vinte para quarenta segundos. A linha cai novamente para uma aceleração negativa de quarenta para cinquenta segundos. — Figura\(\PageIndex{10}\): (a) Posição do trem ao longo do tempo. Observe que a posição do trem muda lentamente no início da viagem e, em seguida, cada vez mais rapidamente à medida que aumenta a velocidade. Sua posição então muda mais lentamente à medida que diminui a velocidade no final da jornada. No meio da jornada, enquanto a velocidade permanece constante, a posição muda a uma taxa constante. (b) Velocidade do trem ao longo do tempo. A velocidade do trem aumenta à medida que acelera no início da viagem. Continua o mesmo no meio da jornada (onde não há aceleração). Ele diminui à medida que o trem desacelera no final da viagem. (c) A aceleração do trem ao longo do tempo. O trem tem aceleração positiva, pois acelera no início da viagem. Ele não tem aceleração, pois viaja em velocidade constante no meio da jornada. Sua aceleração é negativa, pois diminui a velocidade no final da jornada.

Exemplo\(\PageIndex{6}\): Calculating Average Velocity: The Subway Train

Qual é a velocidade média do trem na parte b do Exemplo\(\PageIndex{2}\), e mostrada novamente abaixo, se levar 5,00 min para fazer sua viagem?

O trem se move para a esquerda, de uma posição inicial de 5 pontos 25 quilômetros para uma posição final de 3 pontos 75 quilômetros. — Figura\(\PageIndex{11}\)

Estratégia

A velocidade média é o deslocamento dividido pelo tempo. Aqui será negativo, já que o trem se move para a esquerda e tem um deslocamento negativo.

Solução

Identifique os conhecidos. \[ x'_f=3.75 km,\, x'_0=5.25 km,\, Δt=5.00 min. \nonumber\]
Determine o deslocamento,\(Δx'\). Descobrimos\( Δx'\) que estamos\( −1.5 km\) em Example\(\PageIndex{7}\).
Resolva a velocidade média. \[\bar{v}=\dfrac{Δx'}{Δt}=\dfrac{−1.50 km}{5.00 min} \nonumber\]
Converta unidades. \[\bar{v}=\dfrac{Δx'}{Δt}=(\dfrac{−1.50 km}{5.00 min})(\dfrac{60 min}{1 }h)=−18.0 km/h \nonumber\]

Discussão

A velocidade negativa indica movimento para a esquerda.

Exemplo\(\PageIndex{7}\): Calculating Deceleration: The Subway Train

Finalmente, suponha que o trem na Figura\(\PageIndex{7}\) desacelere até parar de uma velocidade de 20,0 km/h em 10,0 s. Qual é sua aceleração média?

Estratégia

Mais uma vez, vamos desenhar um esboço:

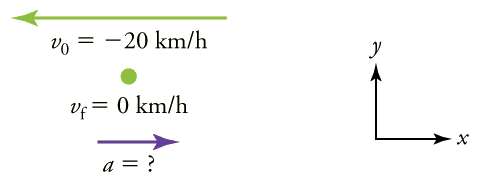
Uma seta vetorial de velocidade apontando para a esquerda com velocidade inicial de menos vinte pontos 0 quilômetros por hora e uma velocidade final de 0. Uma seta vetorial de aceleração apontando para a direita, rotulada como ponto de interrogação igual. — Figura\(\PageIndex{12}\): Como antes, devemos encontrar a mudança na velocidade e a mudança no tempo para calcular a aceleração média.

Solução

Identifique os conhecidos. \(v_0=−20\, km/h\),\(v_f=0\, km/h\),\(Δt=10.0\, s\).
Calcule\(Δv\). A mudança na velocidade aqui é realmente positiva, já que\[Δv=v_f−v_0=0−(−20\, km/h)=+20\, km/h. \nonumber\]
Resolver para\(\bar{ a}\). \[\bar{a}=\dfrac{Δv}{Δt}=\dfrac{+20.0\, km/h}{10.0\, s} \nonumber\]
Converta unidades. \[\bar{a}=\left(\dfrac{+20.0 \,km/h}{10.0\, s}\right)\left(\dfrac{10^3\,m}{1\, km}\right)\left(\dfrac{1\, h}{3600 \,s}\right)=+0.556\, m/^s2 \nonumber\]

Discussão

O sinal de mais significa que a aceleração está à direita. Isso é razoável porque o trem inicialmente tem uma velocidade negativa (à esquerda) nesse problema e uma aceleração positiva se opõe ao movimento (e assim é para a direita). Novamente, a aceleração está na mesma direção da mudança na velocidade, que é positiva aqui. Como no exemplo\(\PageIndex{5}\), essa aceleração pode ser chamada de desaceleração, pois está na direção oposta à velocidade.

Signo e direção

Talvez a coisa mais importante a ser observada sobre esses exemplos sejam os sinais das respostas. Em nosso sistema de coordenadas escolhido, mais significa que a quantidade está à direita e menos significa que está à esquerda. Isso é fácil de imaginar para deslocamento e velocidade. Mas é um pouco menos óbvio para aceleração. A maioria das pessoas interpreta a aceleração negativa como a desaceleração de um objeto. Esse não foi o caso em Example\(\PageIndex{5}\), onde uma aceleração positiva diminuiu uma velocidade negativa. A distinção crucial era que a aceleração estava na direção oposta à velocidade. Na verdade, uma aceleração negativa aumentará a velocidade negativa. Por exemplo, o trem que se move para a esquerda na Figura Figura\(\PageIndex{11}\) é acelerado por uma aceleração para a esquerda. Nesse caso, v e a são negativos. Os sinais de mais e menos indicam as direções das acelerações. Se a aceleração tiver o mesmo sinal da velocidade, o objeto está acelerando. Se a aceleração tiver o sinal oposto à velocidade, o objeto está diminuindo.

Exercício\(\PageIndex{1}\)

Um avião pousa em uma pista que viaja para o leste. Descreva sua aceleração.

Responda: Se tomarmos o leste para ser positivo, então o avião tem aceleração negativa, pois está acelerando em direção ao oeste. Também está desacelerando: sua aceleração é oposta em direção à sua velocidade.

EXPLORAÇÕES PHET: SIMULAÇÃO DE HOMEM EM MOVIMENTO

Aprenda sobre gráficos de posição, velocidade e aceleração com a simulação PhET Moving Man. Mova o homenzinho para frente e para trás com o mouse e desenhe seu movimento. Defina a posição, a velocidade ou a aceleração e deixe a simulação mover o homem para você.

Resumo

Aceleração é a taxa na qual a velocidade muda. Em símbolos, a aceleração média\(\bar{ a}\) é\(\bar{a}=\dfrac{Δv}{Δt}=\dfrac{v_f−v_0}{t_f−t_0}\).
A unidade SI para aceleração é 2.
A aceleração é um vetor e, portanto, tem uma magnitude e uma direção.
A aceleração pode ser causada por uma mudança na magnitude ou na direção da velocidade.
A aceleração instantânea é a aceleração em um instante específico no tempo.
A desaceleração é uma aceleração com uma direção oposta à da velocidade.

Glossário

aceleração: a taxa de mudança na velocidade; a mudança na velocidade ao longo do tempo

aceleração média: a mudança na velocidade dividida pelo tempo em que ela muda

aceleração instantânea: aceleração em um ponto específico no tempo

desaceleração: aceleração na direção oposta à velocidade; aceleração que resulta em uma diminuição na velocidade