7.5: Formas da equação de uma reta

Last updated
Save as PDF

Page ID: 170095

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A seção anterior explicou as equações das linhas verticais e horizontais. Agora descubra mais três formas das equações de uma reta, a saber, a Forma de Intercepção de Inclinação, a Forma de Ponto-Inclinação e a Forma Padrão.

Forma de interceptação de inclinação da equação de uma reta

Definição: Forma de interceptação de inclinação

A forma de interceptação de inclinação da equação de uma reta tem a forma:

\[y = mx + b \nonumber \]

Onde$m$ está a inclinação da linha e$(0, b)$ é o$y$ −intercepto.

Observe que o$y$ intercepto -é o ponto em que a linha cruza o$y$ eixo −, ou seja, quando$x = 0$.

Exemplo Template:index

Escreva uma equação da linha com os declives e$y$ interceptos fornecidos.

inclinação =$5$;$y$ −interceptar$(0, \dfrac{1}{2})$
inclinação =$−\dfrac{5}{6}$;$y$ − interceptar$(0, −\dfrac{3}{4})$

Solução

$m = 5$e$b = \dfrac{1}{2}$

A equação de uma reta é do para$y = mx + b$. Assim,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute \(m = 5$e$b = \dfrac{1}{2}$}\ end {array}\)

Portanto,$y = 5x + \dfrac{1}{2}$ é a equação da reta com a inclinação e o$y$ intercepto fornecidos.

Dado$m = −\dfrac{5}{6}$ e$b = −\dfrac{3}{4}$

Assim,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}$

Portanto,$y = −\dfrac{5}{6}x − \dfrac{3}{4}$ é a equação da reta com a inclinação e o$y$ intercepto fornecidos.

Exemplo Template:index

Identifique a inclinação e$y$ −intercepte e use-os para representar graficamente cada linha.

$y = −2x + 4$
$5y − 3x = 10$

Solução

a. Observe que a equação linear dada está na forma de interceptação de inclinação. Então,$m = −2$ ou equivalentemente,$m = −\dfrac{2}{1}$ e$b = 4$

$m$é a inclinação da linha, então$m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}$. Para representar graficamente a linha, plote pelo menos dois pontos. Comece com o$y$ −intercept$(0, 4)$ e desça a$2$ unidade e depois vá para a$1$ unidade direita para traçar o segundo ponto. Agora junte os dois pontos com uma linha reta, conforme mostrado na figura abaixo.

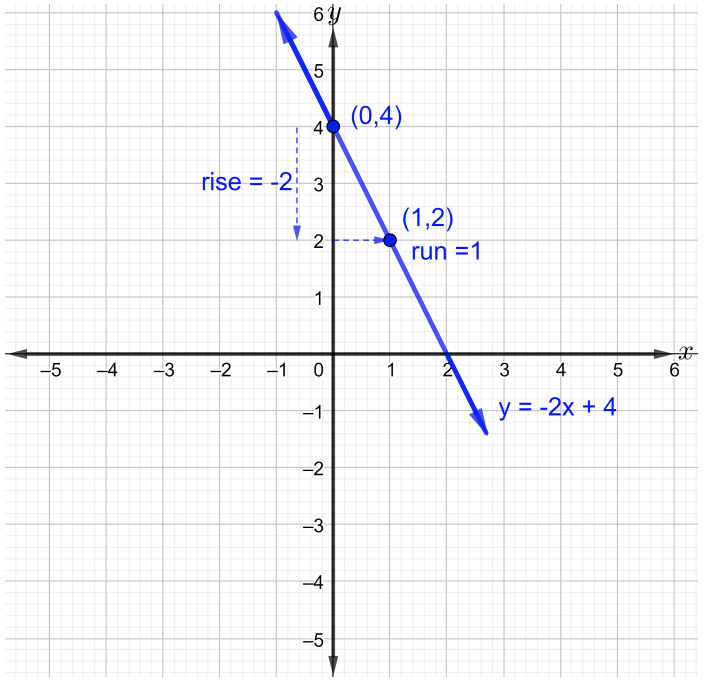
$clipboard_e5fcc0c548a6809df50a713b48295362a.png$

b. Observe que não está claro como identificar a inclinação e a$y$ interceptação nesta equação linear dada porque ela não está na forma de interceptação de inclinação. Assim, resolva$y$ para ter a equação na forma de interceptação de inclinação da seguinte forma,

$\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add \(3x$em ambos os lados da equação}\\ &y =\ dfrac {3} {5} x − 2 &\ text {Divida todos os termos por$5$ para isolar$y$}\ end {array}\)

Agora,$m = \dfrac{3}{5}$$b = −2$ e. Comece traçando o$y$ intercepto -e, em$(0, −2)$ seguida, mova$3$ as unidades para cima e$5$ as unidades para a direita e plote o segundo ponto que é$(5, 1)$. Agora, junte os dois pontos, ou seja,$(0, −2)$ e$(5, 1)$ para obter o gráfico da linha mostrado na figura abaixo.

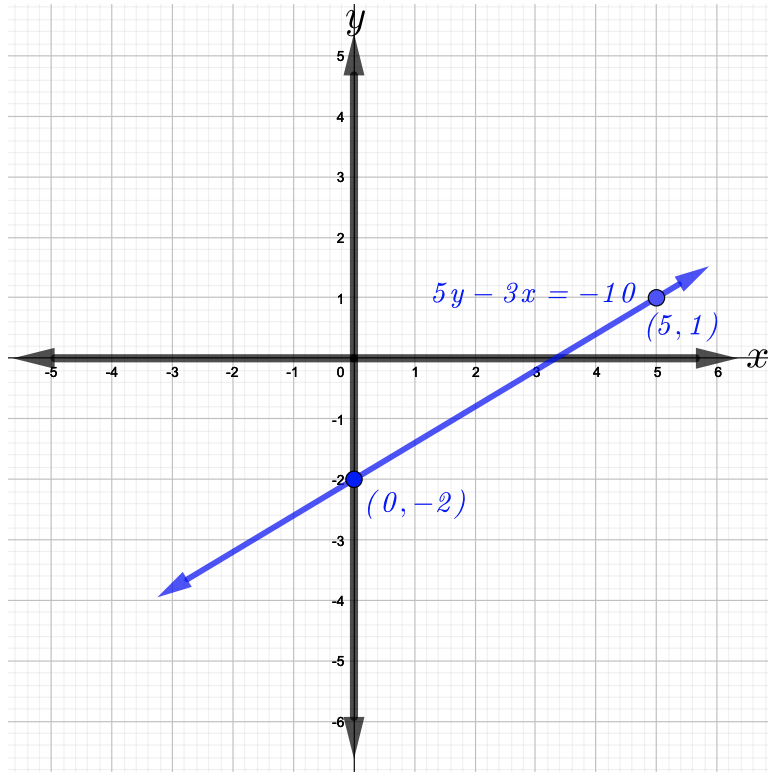
$clipboard_eca3205bebd002556f4570dc0193cd9f6.png$

Exercício Template:index

Escreva uma equação de uma linha com a inclinação e o$y$ -intercepto fornecidos.

inclinação:$2$$y$ -intercepto:$(0, \dfrac{3}{4})$
inclinação:$\dfrac{5}{7}$$y$ -intercepto:$(0, −6)$
inclinação:$−\dfrac{1}{2}$$y$ -intercepto:$(0, −\dfrac{7}{11} )$

Exercício Template:index

Identifique a inclinação e o$y$ -intercepte e use-os para representar graficamente cada linha.

$y = 5x − 3$
$2y = −6x + 1$

Forma de inclinação pontual da equação de uma reta

Definição: Forma de inclinação de pontos

A forma de inclinação de pontos da equação de uma linha reta é:

\[y − y_1 = m(x − x_1) \nonumber \]

Onde$m$ está a inclinação da linha e$(x_1, y_1)$ é qualquer ponto na linha reta.

Exemplo Template:index

Encontre a equação de cada linha que passa pelo ponto determinado e pela inclinação dada.

Inclinação$3$ e ponto$(−1, 8)$
Inclinação$−\dfrac{5}{2}$ e ponto$(\dfrac{4}{3}, \dfrac{1}{3})$

Solução

Para encontrar a equação da reta através do ponto$(−1, 8)$ com inclinação$m = 3$, use a forma de inclinação do ponto da seguinte forma:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute \(m = 3$,$x_1 = −1$, e$y_1 = 8$}\\ &y − 8 = 3 (x + 1) &\ text {Simplifique}\\ &y − 8 = 3x + 3 &\ text {Multiplique os dois termos à direita da equação por$3$}\\ &y = 3x + 11 &\ text {Adicione$8$ aos dois lados da igualdade para isolar$y$}\ end {array}\)

Portanto,$y = 3x + 11$ é a equação da reta com a inclinação e o ponto dados. A linha está na forma de interceptação de inclinação.

Semelhante à parte a, use a Forma de Inclinação de Pontos da seguinte forma:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute \(m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}$, e$y_1 = −\dfrac{1}{3}$}\\ &y +\ dfrac {1} {3} = −\ dfrac {5} {2} x +\ dfrac {20} {6} &\ text {Distribuir e simplificar}\\ &y = −\ dfrac {5} {2} x +\ dfrac {20} {6} −\ dfrac {1} {3} &\ texto {Subtrair$\dfrac{1}{3}$ de ambos os lados}\\ &y = −\ dfrac {5} {2} x + 3 &\ text {Para combinar as duas frações, observe que o LCD$= 6$.}\\ & &\ text {Multiplique o numerador e o denominador de$\dfrac{1}{3}$ por$2$ e simplifique:}\\ & & &\ text {$\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3$}\ end {array}\)

Portanto,$y = −\dfrac{5}{2}x + 3$ é a equação da reta que passa pelo ponto dado e pela inclinação dada.

Exemplo Template:index

Encontre uma equação da linha dada aos pontos$(2, 4)$$(−3, 9)$ e.

Observe que, no início deste capítulo, ele explicou como encontrar uma equação de uma reta dada uma inclinação e um$y$ intercepto. Este capítulo também explicou como encontrar uma equação de uma reta dado qualquer ponto da reta e uma inclinação. Então, em ambos os métodos, a inclinação é dada.

Solução

Para encontrar uma equação de uma reta dados dois pontos na linha, primeiro encontre a inclinação usando a inclinação da fórmula da linha. Depois, aplique a forma de inclinação de pontos com qualquer um dos pontos fornecidos. Primeiro, use os dois pontos para encontrar a inclinação da linha. Deixe$(x_1, y_1) = (2, 4)$$(x_2, y_2) = (−3, 9)$ e. Em seguida,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}$

Agora, a inclinação foi encontrada, então encontre a equação da reta usando qualquer um dos pontos fornecidos. Portanto,$m = −1$ considere usar o ponto$(2, 4)$.

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute \(m = −1$,$x_1 = 2$,$y_1 = 4$}\\ &y − 4 = −x + 2 &\ text {$-1$Distribua para os dois termos à direita}\\ &y = −x + 6 &\ text {Adicione$4$ aos dois lados da equação para isolar$y$}\ end {array}\)

Portanto,$y = −x + 6$ é a equação da reta que passa pelo ponto de referência e tem a forma de interceptação de inclinação.

Exercício Template:index

Encontre a equação de cada linha que passa pelo ponto dado e tem a inclinação dada.

A inclinação$−\dfrac{5}{2}$ e o ponto$(3, 0)$.
A inclinação$\dfrac{1}{2}$ e o ponto$(−2, −3)$.

Exercício Template:index

Encontre uma equação da reta dados os seguintes pontos.

$(−9, −3)$e$(6, −2)$
$(4, 1)$e$(−2, 2)$

Forma padrão da equação de uma reta (também conhecida como forma geral de uma equação linear)

Definição: Formulário padrão

A forma padrão de uma linha não vertical está na forma

\[Ax + By = C \nonumber \]

Onde$A$ é um número inteiro positivo$B$ e$C$ são números inteiros com$B \neq 0$.

Exemplo Template:index

Faça um gráfico de cada linha das seguintes equações:

$4x − 3y = 6$
$\dfrac{1}{2} − y + 1 = 0$

Observe que o$x$ intercepto -é o ponto em que a linha cruza o$x$ eixo -. Ou seja, quando$y = 0$. Assim, o$x$ intercepto -é um ponto da forma$(a, 0)$, onde$a$ está qualquer número real.

Solução

A equação$4x − 3y = 6$ está na forma padrão. Para representar graficamente a linha da equação dada, pode ser possível usar mais de um método. Por exemplo, resolvendo$y$ para obter a equação na forma de interceptação de inclinação e, em seguida, representar graficamente a linha. Também é possível encontrar dois pontos e, em seguida, representar graficamente a linha. Os dois pontos mais fáceis de encontrar rapidamente são as$y$ interceptações$x$ e. Portanto, esse método é recomendado.

Para encontrar o$x$ intercepto -,$y = 0$ defina a equação dada e resolva da$x$ seguinte forma,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute \(y = 0$}\\ &4x = 6 &\ text {Simplifique}\\ &x =\ dfrac {6} {4} &\ text {Divida pelos$4$ dois lados da equação}\\ &x =\ dfrac {3} {2} &\ text {Simplifique}\ end {array}\)

Portanto, o$x$ intercepto -é o ponto$(\dfrac{3}{2}, 0)$

Agora, para encontrar o$y$ -intercept, defina da$x = 0$ seguinte forma,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute \(x = 0$}\\ &−3y = 6 &\ text {Simplifique}\\ &y = 6 −3 &\ text {Divida pelos$−3$ dois lados da equação}\\ &y = −2 &\ text {Simplifique}\ end {array}\)

Agora, plote os pontos$(\dfrac{3}{2}, 0)$$(0, −2)$ e faça um gráfico da linha reta que passa por eles, conforme mostrado na figura abaixo.

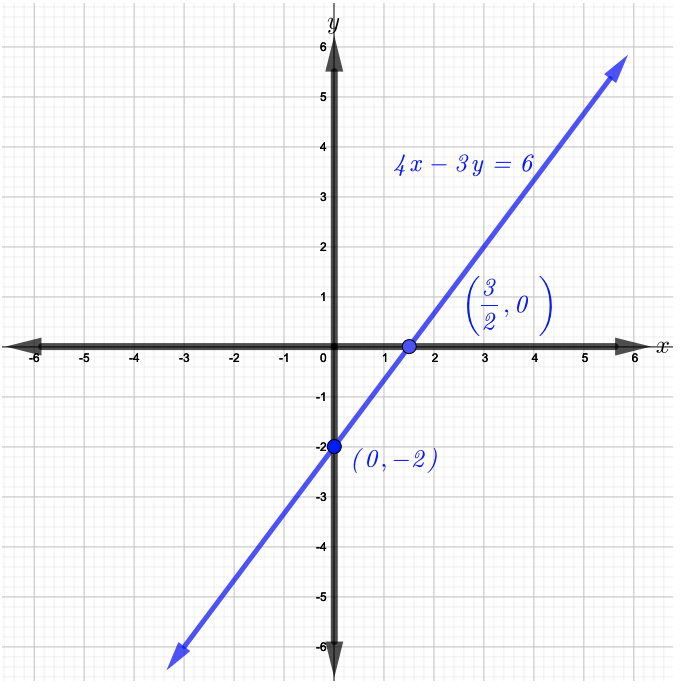
$clipboard_ede795f89eb03e5b448b62ec8dc0b7663.png$

A equação não$\dfrac{1}{2} x − y + 1 = 0$ está na forma padrão. Então, subtraia$1$ de ambos os lados da equação para ter$\dfrac{1}{2}x − y = −1$ o que agora está na forma padrão.

Novamente, semelhante à parte b, encontre as$y$ interceptações$x$ e. Primeiro, encontre o$x$ -intercept definindo$y = 0$ e resolva da$x$ seguinte forma.

$ \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute \(y = 0$}\\ &\ dfrac {1} {2} x = −1 &\ text {Simplifique}\\ &x = −2 &\ text {Multiplique pelos$2$ dois lados da equação.} \ end {matriz}\)

Assim, o$x$ intercepto -é o ponto$(−2, 0)$.

Agora,$x = 0$ defina para encontrar o$y$ intercepto -, da seguinte forma,

$ \begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute \(x = 0$}\\ &−y = −1 &\ text {Simplifique}\\ &y = 1 &\ text {Multiplique por$-1$.} \ end {matriz}\)

Portanto, o$y$ intercepto -é$(0, 1)$.

Faça um gráfico dos$y$ interceptos$x$$(−2, 0)$ e e, em seguida$(0, 1)$, represente graficamente a linha reta que passa por eles, conforme mostrado na figura abaixo.

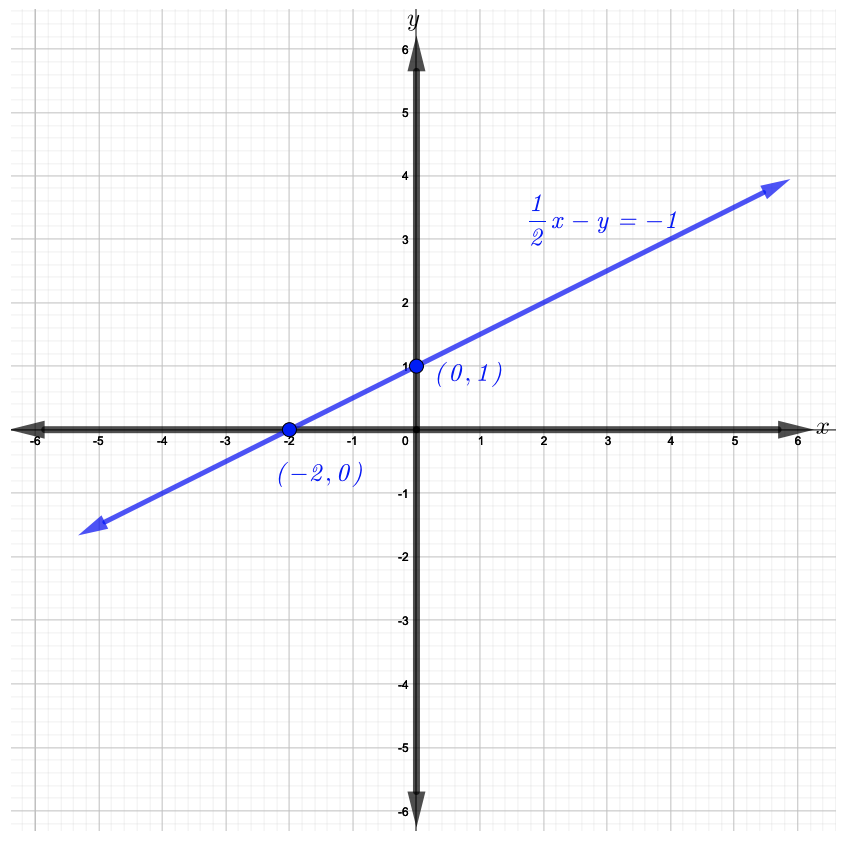
$clipboard_e3475016017c80b2298d3517f4bef3bf0.png$

Não há lição de casa para esta seção.