1.3: Números inteiros
- Page ID
- 183324
Ao final desta seção, você poderá:
- Simplifique expressões com valor absoluto
- Adicione e subtraia números inteiros
- Multiplique e divida números inteiros
- Simplifique expressões com números inteiros
- Avalie expressões variáveis com números inteiros
- Traduza frases em expressões com números inteiros
- Use números inteiros em aplicativos
Uma introdução mais completa aos tópicos abordados nesta seção pode ser encontrada no capítulo Álgebra Elementar, Fundamentos.
Simplifique expressões com valor absoluto
Um número negativo é um número menor que 0. Os números negativos estão à esquerda de zero na reta numérica (Figura\(\PageIndex{1}\)).
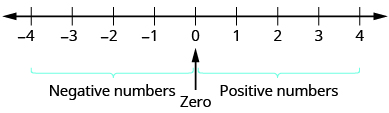
Figura\(\PageIndex{1}\). A linha numérica mostra a localização dos números positivos e negativos.
Você deve ter notado que, na reta numérica, os números negativos são uma imagem espelhada dos números positivos, com zero no meio. Como os números\(2\)\(−2\) estão à mesma distância de zero, cada um é chamado de oposto ao outro. O oposto de\(2\) é\(−2\) e o oposto de\(−2\) é\(2\).
O oposto de um número é o número que está à mesma distância de zero na reta numérica, mas no lado oposto de zero.
A figura\(\PageIndex{2}\) ilustra a definição.

Figura\(\PageIndex{2}\). O oposto de 3 é\(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
Vimos que números como 3 e −3 são opostos porque estão à mesma distância de 0 na reta numérica. Ambos estão a três unidades de 0. A distância entre 0 e qualquer número na reta numérica é chamada de valor absoluto desse número.
O valor absoluto de um número é sua distância de 0 na reta numérica.
O valor absoluto de um número\(n\) é escrito como\(|n|\) e\(|n|≥0\) para todos os números.
Os valores absolutos são sempre maiores ou iguais a zero.
Por exemplo,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
A figura\(\PageIndex{3}\) ilustra essa ideia.
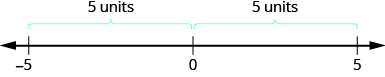
O valor absoluto de um número nunca é negativo porque a distância não pode ser negativa. O único número com valor absoluto igual a zero é o próprio número zero porque a distância de 0 a 0 na reta numérica é zero unidades.
No próximo exemplo, vamos ordenar expressões com valores absolutos.
Preencha\(<,\,>,\) ou\(=\) para cada um dos seguintes pares de números:
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ text {− (−16) __|−16|}\).
- Resposta
-
uma.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
b.
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
d.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
Preencha\(<,\,>,\) ou\(=\) para cada um dos seguintes pares de números:
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- Resposta
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
Preencha\(<,>,\) ou\(=\) para cada um dos seguintes pares de números:
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- Resposta
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
Agora adicionamos barras de valor absoluto à nossa lista de símbolos de agrupamento. Quando usamos a ordem das operações, primeiro simplificamos o máximo possível dentro das barras de valor absoluto e, em seguida, tomamos o valor absoluto do número resultante.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
No próximo exemplo, simplificaremos primeiro as expressões dentro das barras de valor absoluto, assim como fazemos com parênteses.
Simplifique:\(\mathrm{24−|19−3(6−2)|}\).
- Resposta
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
Simplifique:\(19−|11−4(3−1)|\).
- Resposta
-
16
Simplifique:\(9−|8−4(7−5)|\).
- Resposta
-
9
Adicionar e subtrair números inteiros
Até agora, em nossos exemplos, usamos apenas os números de contagem e os números inteiros.
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
Nosso trabalho com opostos nos dá uma maneira de definir os números inteiros. Os números inteiros e seus opostos são chamados de números inteiros. Os números inteiros são os números\(…−3,−2,−1,0,1,2,3…\)
Os números inteiros e seus opostos são chamados de números inteiros.
Os números inteiros são os números
\[…-3,-2,-1,0,1,2,3…,\]
A maioria dos estudantes se sente confortável com os fatos de adição e subtração para números positivos. Mas fazer adição ou subtração com números positivos e negativos pode ser mais desafiador.
Usaremos dois contadores de cores para modelar a adição e a subtração de negativos para que você possa visualizar os procedimentos em vez de memorizar as regras.
Deixamos que uma cor (azul) represente o positivo. A outra cor (vermelha) representará os negativos.

Se tivermos um contador positivo e um contador negativo, o valor do par será zero. Eles formam um par neutro. O valor desse par neutro é zero.
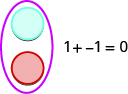
Usaremos os contadores para mostrar como adicionar:
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
O primeiro exemplo\(5+3,\) adiciona 5 positivos e 3 positivos — ambos positivos.
O segundo exemplo,\(−5+(−3),\) soma 5 negativos e 3 negativos — ambos negativos.
Quando os sinais são iguais, os contadores são todos da mesma cor, então nós os adicionamos. Em cada caso, obtemos 8 — 8 positivos ou 8 negativos.

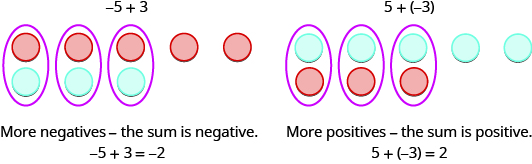
Então, o que acontece quando os sinais são diferentes? Vamos adicionar\(−5+3\)\(5+(−3)\) e.
Quando usamos contadores para modelar a adição de números inteiros positivos e negativos, é fácil ver se há mais contadores positivos ou mais negativos. Então, sabemos se a soma será positiva ou negativa.
Adicionar: ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\).
- Resposta
-
ⓐ
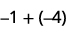

1 negativo mais 4 negativos é 5 negativos 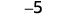
ⓑ
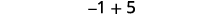

Há mais pontos positivos, então a soma é positiva. 
ⓒ
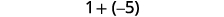

Há mais negativos, então a soma é negativa. 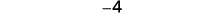
Adicionar: ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\).
- Resposta
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
Adicionar: ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\).
- Resposta
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
Continuaremos a usar contadores para modelar a subtração. Talvez quando você era mais jovem, você lesse\(“5−3”\) como “5 menos 3”. Quando você usa contadores, você pode pensar em subtração da mesma maneira!
Usaremos os contadores para mostrar para subtrair:
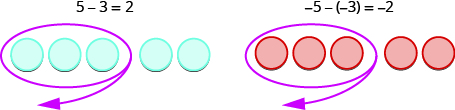
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
No primeiro exemplo\(5−3\), subtraímos 3 positivos de 5 positivos e terminamos com 2 positivos.
No segundo exemplo,\(−5−(−3),\) subtraímos 3 negativos de 5 negativos e terminamos com 2 negativos.
Cada exemplo usava contadores de apenas uma cor, e o modelo de subtração “take away” era fácil de aplicar.
O que acontece quando temos que subtrair um número positivo e um negativo? Precisaremos usar contadores azuis e vermelhos, bem como alguns pares neutros. Se não tivermos o número de contadores necessários para retirar, adicionamos pares neutros. Adicionar um par neutro não altera o valor. É como trocar quartos por níquel — o valor é o mesmo, mas parece diferente.
Vamos dar uma olhada em\(−5−3\)\(5−(−3)\) e.
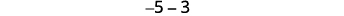 |
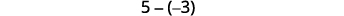 |
|
| Modele o primeiro número. |  |
 |
| Agora adicionamos os pares neutros necessários. |  |
 |
| Removemos o número de contadores modelados pelo segundo número. | 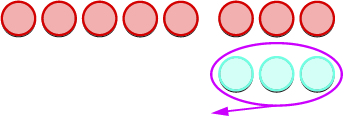 |
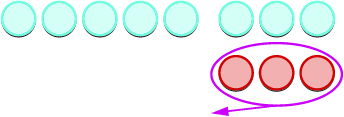 |
| Conte o que sobrou. |  |
 |
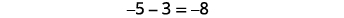 |
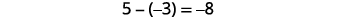 |
|
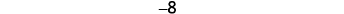 |
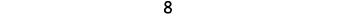 |
Subtraia: ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\).
- Resposta
-
ⓐ
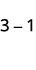
Pegue 1 positivo de 3 positivos e obtenha 2 positivos. 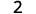
ⓑ

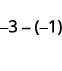
Pegue 1 positivo de 3 negativos e obtenha 2 negativos. 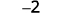
ⓒ

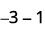
Pegue 1 positivo do único par neutro adicionado. 
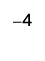
ⓓ

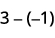
Pegue 1 negativo do único par neutro adicionado. 

Subtraia: ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\).
- Resposta
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
Subtraia: ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\).
- Resposta
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
Você notou que a subtração de números assinados pode ser feita adicionando o oposto? No último exemplo,\(−3−1\) é o mesmo que\(−3+(−1)\) e\(3−(−1)\) é o mesmo que\(3+1\). Muitas vezes você verá essa ideia, a propriedade de subtração, escrita da seguinte forma:
\[a−b=a+(−b)\]
Subtrair um número é o mesmo que somar seu oposto.
Simplifique: ⓐ\(13−8\)\(−17−9\) e\(13+(−8)\) ⓑ\(9−(−15)\) e\(−17+(−9)\) ⓒ\(−7−(−4)\) e\(9+15\) ⓓ\(−7+4\) e.
- Resposta
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
Simplifique: ⓐ\(21−13\)\(−11−7\) e\(21+(−13)\) ⓑ\(6−(−13)\) e\(−11+(−7)\) ⓒ\(−5−(−1)\) e\(6+13\) ⓓ\(−5+1\) e.
- Resposta
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
Simplifique: ⓐ\(15−7\)\(−14−8\) e\(15+(−7)\) ⓑ\(4−(−19)\) e\(−14+(−8)\) ⓒ\(−4−(−7)\) e\(4+19\) ⓓ\(−4+7\) e.
- Resposta
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
O que acontece quando há mais de três números inteiros? Nós apenas usamos a ordem das operações normalmente.
Simplifique:\(7−(−4−3)−9.\)
- Resposta
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
Simplifique:\(8−(−3−1)−9.\)
- Resposta
-
3
Simplifique:\(12−(−9−6)−14.\)
- Resposta
-
13
Multiplique e divida números inteiros
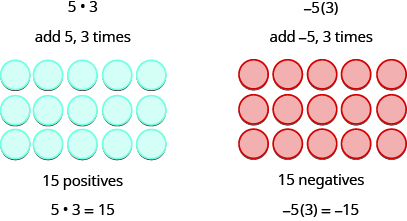
Como a multiplicação é uma abreviatura matemática para adição repetida, nosso modelo pode ser facilmente aplicado para mostrar a multiplicação de números inteiros. Vamos dar uma olhada nesse modelo concreto para ver quais padrões observamos. Usaremos os mesmos exemplos que usamos para adição e subtração. Aqui, estamos usando o modelo apenas para nos ajudar a descobrir o padrão.
Lembramos que a⋅ba·b significa adicionar a, b vezes.
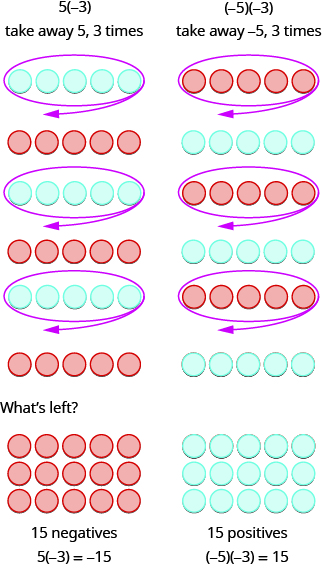
Os próximos dois exemplos são mais interessantes. O que significa multiplicar 5 por −3? Isso significa subtrair 5,3 vezes. Encarar a subtração como “tirar”, significa tirar 5, 3 vezes. Mas não há nada para retirar, então começamos adicionando pares neutros no espaço de trabalho.
Em resumo:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Observe que, para a multiplicação de dois números assinados, quando o
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
E quanto à divisão? A divisão é a operação inversa da multiplicação. Então,\(15÷3=5\) porque\(15·3=15\). Em palavras, essa expressão diz que 15 podem ser divididos em 3 grupos de 5 cada porque somar cinco três vezes dá 15. Se você observar alguns exemplos de multiplicação de números inteiros, poderá descobrir as regras para dividir números inteiros.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
A divisão segue as mesmas regras da multiplicação em relação aos sinais.
Para multiplicação e divisão de dois números assinados:
| Mesmos sinais | Resultado |
|---|---|
| • Dois pontos positivos | Positivo |
| • Dois negativos | Positivo |
Se os sinais forem os mesmos, o resultado será positivo.
| Sinais diferentes | Resultado |
|---|---|
| • Positivo e negativo | Negativo |
| • Negativo e positivo | Negativo |
Se os sinais forem diferentes, o resultado será negativo.
Multiplique ou divida: ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- Responda
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
Multiplique ou divida: ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- Responda
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
Multiplique ou divida: ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\).
- Responda
-
ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7
Quando multiplicamos um número por 1, o resultado é o mesmo número. Cada vez que multiplicamos um número por −1, obtemos o oposto!
\[−1a=−a\]
Multiplicar um número por\(−1\) dá o oposto.
Simplifique expressões com números inteiros
O que acontece quando há mais de dois números em uma expressão? A ordem das operações ainda se aplica quando os negativos são incluídos. Lembra, por favor, desculpe minha querida tia Sally?
Vamos tentar alguns exemplos. Simplificaremos expressões que usam todas as quatro operações com números inteiros: adição, subtração, multiplicação e divisão. Lembre-se de seguir a ordem das operações.
Simplifique: ⓐ\((−2)^4\) ⓑ\(−2^4\).
- Responda
-
Observe a diferença nas partes (a) e (b). Em parte (a), o expoente significa elevar o que está entre parênteses, de −2 à 4ª potência. Na parte (b), o expoente significa aumentar apenas a potência 2 à 4ª e, em seguida, pegar o oposto.
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
Simplifique: ⓐ\((−3)^4\) ⓑ\(−3^4\).
- Responda
-
ⓐ 81 ⓑ −81
Simplifique: ⓐ\((−7)^2\) ⓑ\(−7^2\).
- Responda
-
ⓐ 49 ⓑ −49
O último exemplo nos mostrou a diferença entre\((−2)^4\)\(−2^4\) e. Essa distinção é importante para evitar erros futuros. O próximo exemplo nos lembra de multiplicar e dividir da esquerda para a direita.
Simplifique: ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\).
- Responda
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
Simplifique: ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- Responda
-
ⓐ 4 ⓑ 21
Simplifique: ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- Responda
-
ⓐ 9 ⓑ 6
Avalie expressões variáveis com números inteiros
Lembre-se de que avaliar uma expressão significa substituir um número pela variável na expressão. Agora podemos usar números negativos e números positivos.
Avalie\(4x^2−2xy+3y^2\) quando\(x=2,y=−1\).
- Responda
-
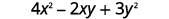
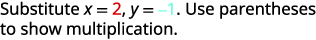
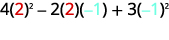
Simplifique os expoentes 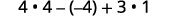
Multiplique. 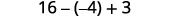
Subtrair. 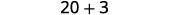
Adicionar. 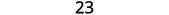
Avalie:\(3x^2−2xy+6y^2\) quando\(x=1,y=−2\).
- Responda
-
31
Avalie:\(4x^2−xy+5y^2\) quando\(x=−2,y=3\).
- Responda
-
67
Traduza frases em expressões com números inteiros
Nosso trabalho anterior traduzindo inglês para álgebra também se aplica a frases que incluem números positivos e negativos.
Traduza e simplifique: a soma de 8 e −12, aumentada em 3.
- Responda
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
Traduza e simplifique a soma de 9 e −16, aumentada em 4.
- Responda
-
\((9+(−16))+4;−3\)
Traduza e simplifique a soma de −8 e −12, aumentada em 7.
- Responda
-
\((−8+(−12))+7;−13\)
Use números inteiros em aplicativos
Vamos delinear um plano para resolver aplicativos. É difícil encontrar algo se não sabemos o que estamos procurando ou como chamá-lo! Então, quando resolvemos um aplicativo, primeiro precisamos determinar o que o problema está solicitando que encontremos. Em seguida, escreveremos uma frase que forneça as informações para encontrá-la. Vamos traduzir a frase em uma expressão e depois simplificá-la para obter a resposta. Finalmente, resumimos a resposta em uma frase para garantir que ela faça sentido.
A temperatura em Kendallville, Indiana, certa manhã, era de 11 graus. No meio da tarde, a temperatura havia caído para −9−9 graus. Qual foi a diferença nas temperaturas da manhã e da tarde?
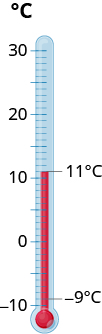
- Responda
-






A temperatura em Anchorage, Alasca, em uma manhã, foi de 15 graus. No meio da tarde, a temperatura havia caído para 30 graus abaixo de zero. Qual foi a diferença nas temperaturas da manhã e da tarde?
- Responda
-
A diferença nas temperaturas foi de 45 graus Fahrenheit.
A temperatura em Denver era de −6 graus na hora do almoço. Ao pôr do sol, a temperatura havia caído para -15 graus. Qual foi a diferença nas temperaturas da hora do almoço e do pôr do sol?
- Responda
-
A diferença nas temperaturas foi de 9 graus.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas.
- Identifique o que devemos encontrar.
- Escreva uma frase que forneça as informações para encontrá-la.
- Traduza a frase para uma expressão.
- Simplifique a expressão.
- Responda à pergunta com uma frase completa.
Acesse esse recurso on-line para obter instruções e práticas adicionais com números inteiros.
- Subtração de números inteiros com contadores
Conceitos-chave
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- O valor absoluto de um número é sua distância de 0 na reta numérica.
O valor absoluto de um número n é escrito como\(|n|\) e\(|n|≥0\) para todos os números.
Os valores absolutos são sempre maiores ou iguais a zero.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- Propriedade de subtração
\(a−b=a+(−b)\)
Subtrair um número é o mesmo que adicionar seu oposto. - Para multiplicação e divisão de dois números assinados:
Se os sinais forem os mesmos, o resultado será positivo.Mesmos sinais Resultado • Dois pontos positivos Positivo • Dois negativos Positivo
Se os sinais forem diferentes, o resultado será negativo.Sinais diferentes Resultado • Positivo e negativo Negativo • Negativo e positivo Negativo - Multiplicação por\(−1\)
\(−1a=−a\)
Multiplicar um número por\(−1\) dá o oposto.
- Como usar números inteiros em aplicativos.
- Leia o problema. Certifique-se de que todas as palavras e ideias sejam compreendidas
- Identifique o que devemos encontrar.
- Escreva uma frase que forneça as informações para encontrá-la.
- Traduza a frase para uma expressão.
- Simplifique a expressão.
- Responda à pergunta com uma frase completa.
Glossário
- valor absoluto
- O valor absoluto de um número é sua distância da\(0\) reta numérica.
- inteiros
- Os números inteiros e seus opostos são chamados de números inteiros.
- números negativos
- Números menores que\(0\) são números negativos.
- oposta
- O oposto de um número é o número que está à mesma distância de zero na reta numérica, mas no lado oposto de zero.


