Skip to main content
Global

11.4E: Exercícios

  1. Last updated
  2. Save as PDF
  • Page ID
    183742

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A prática leva à perfeição

    Exercício\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    Nos exercícios a seguir, represente graficamente cada elipse.

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    Resposta

    1.

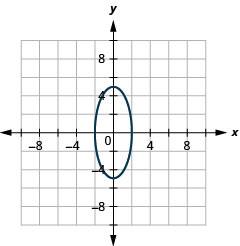
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 5) e (0, menos 5) e pontos finais de eixos menores (2, 0) e (menos 2, 0).
    Figura 11.3.38

    3.

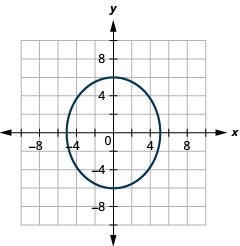
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 6) e (0, menos 6) e pontos finais do eixo menor (5, 0) e (menos 5, 0).
    Figura 11.3.39

    5.

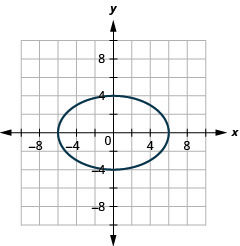
    Este gráfico mostra uma elipse com centro (0, 0), vértices (6, 0) e (menos 6, 0) e pontos finais do eixo menor (0, 4) e (0, menos 4).
    Figura 11.3.40

    7.

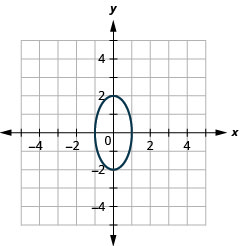
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 2) e (0, menos 2) e pontos finais do eixo menor (1, 0) e (menos 1, 0).
    Figura 11.3.41

    9.

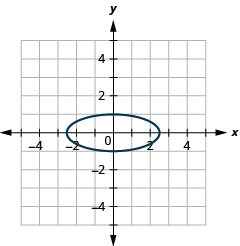
    Este gráfico mostra uma elipse com centro (0, 0), vértices (5, 0) e (menos 5, 0) e pontos finais do eixo menor (0, 2) e (0, menos 2).
    Figura 11.3.42

    11.

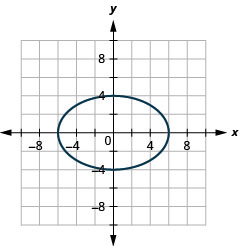
    Este gráfico mostra uma elipse com centro (0, 0), vértices (6, 0) e (menos 6, 0) e pontos finais do eixo menor (0, 4) e (0, menos 4).
    Figura 11.3.43
    Exercício\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    Nos exercícios a seguir, encontre a equação da elipse mostrada no gráfico.

    1.

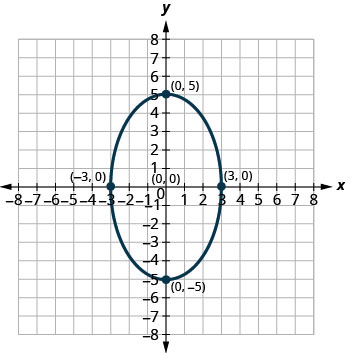
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 5) e (0, menos 5) e pontos finais do eixo menor (menos 3, 0) e (3, 0).
    Figura 11.3.44

    2.

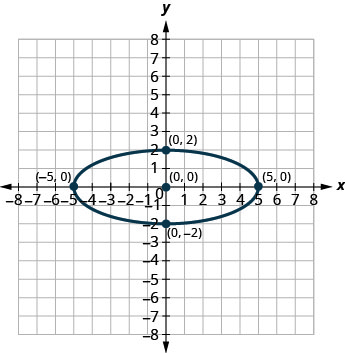
    Este gráfico mostra uma elipse com centro (0, 0), vértices (5, 0) e (menos 5, 0) e pontos finais do eixo menor (0, 2) e (0, menos 2).
    Figura 11.3.45

    3.

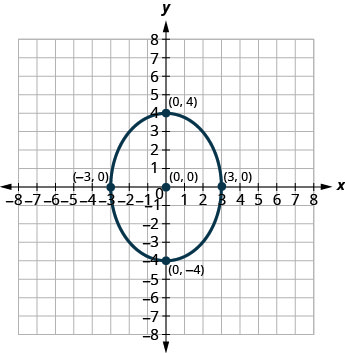
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 4) e (0, menos 4) e pontos finais do eixo menor (menos 3, 0) e (3, 0).
    Figura 11.3.46

    4.

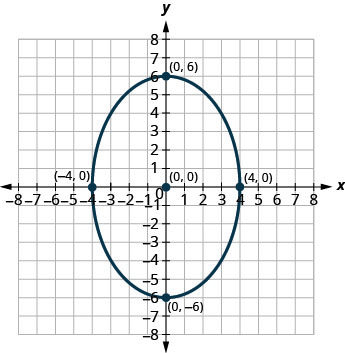
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 6) e (0, menos 6) e pontos finais do eixo menor (menos 4, 0) e (4, 0).
    Figura 11.3.47
    Resposta

    1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    Exercício\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir, represente graficamente cada elipse.

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    Resposta

    1.

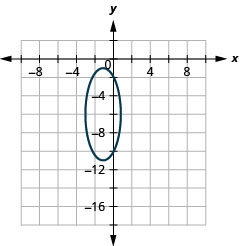
    Este gráfico mostra uma elipse com centro (menos 1, menos 6), vértices (menos 1, menos 1) e (menos 1, menos 11) e pontos finais do eixo menor (menos 3, menos 6) e (1, menos 6).
    Figura 11.3.48

    3.

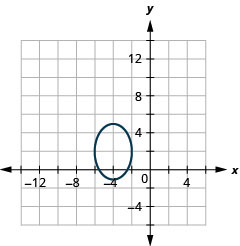
    Este gráfico mostra uma elipse com centro (menos 4, 2), vértices (menos 4, 5) e (menos 4, menos 1) e pontos finais do eixo menor (3, 1) e (menos 6, 2) e (menos 2, 2).
    Figura 11.3.49
    Exercício\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir, represente graficamente cada equação por tradução.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    Resposta

    1.

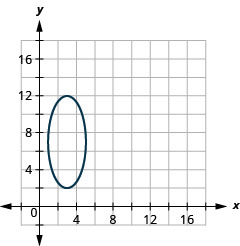
    Este gráfico mostra uma elipse com centro (3, 7), vértices (3, 2) e (3, 12) e pontos finais de eixos menores (1, 7) e (5, 7).
    Figura 11.3.50

    3.

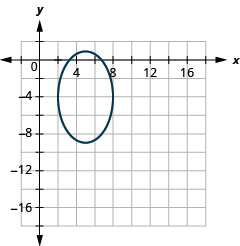
    Este gráfico mostra uma elipse com centro (5, menos 4), vértices (5, 1) e (5, menos 9) e pontos finais do eixo menor (2, menos 4) e (8, menos 4).
    Figura 11.3.51
    Exercício\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir,

    1. Escreva a equação na forma padrão e
    2. Gráfico.
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    Resposta

    1.

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
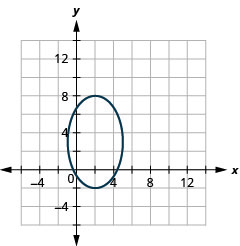
    Este gráfico mostra uma elipse com centro (2, 3), vértices (2, menos 2) e (2, 8) e pontos finais do eixo menor (menos 1, 3) e (5, 3).
    Figura 11.3.52

    3.

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
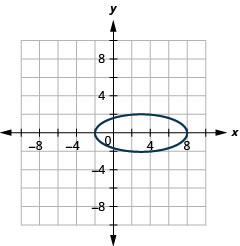
    Este gráfico mostra uma elipse com centro (3, 0), vértices (menos 2, 0) e (8, 0) e pontos finais do eixo menor (3, 2) e (3, menos 2).
    Figura 11.3.53
    Exercício\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    Nos exercícios a seguir, represente graficamente a equação.

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    Resposta

    1.

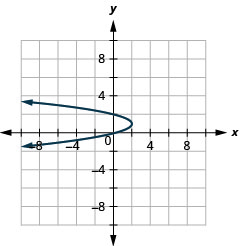
    Este gráfico mostra uma parábola com vértice (2, 1) e interceptos y (0, 0) e (2, 0).
    Figura 11.3.54

    3.

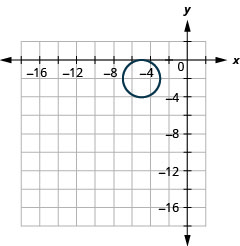
    Este gráfico mostra um círculo com centro (menos 5, menos 2) e um raio de 2 unidades.
    Figura 11.3.55

    5.

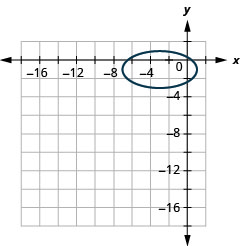
    Este gráfico mostra uma elipse com centro (menos 3, menos 1), vértices (1, menos 1) e (menos 7, menos 1) e pontos finais do eixo menor (menos 3, 1) e (menos 3, menos 3).
    Figura 11.3.56

    7.

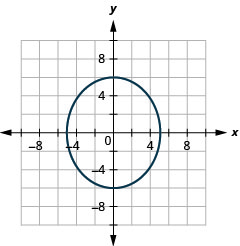
    Este gráfico mostra uma elipse com centro (0, 0), vértices (0, 6) e (0, menos 6) e pontos finais do eixo menor (menos 5, 0) e (5, 0).
    Figura 11.3.57

    9.

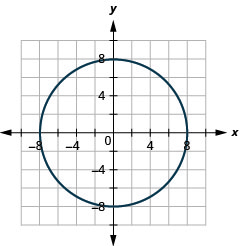
    Este gráfico mostra um círculo com centro (0, 0) e com raio de 8 unidades.
    Figura 11.3.58

    11.

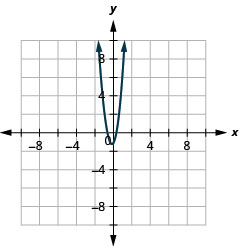
    Este gráfico mostra a parábola de abertura ascendente. Seu vértice tem um valor x ligeiramente menor que 0 e um valor y ligeiramente menor que menos 1. Um ponto nele está aproximadamente em (menos 1, 3).
    Figura 11.3.59
    Exercício\(\PageIndex{21}\) Solve Application with Ellipses

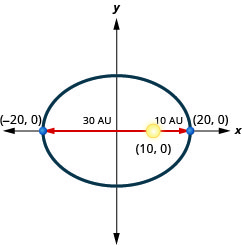
    1. Um planeta se move em uma órbita elíptica ao redor de seu sol. O mais próximo que o planeta chega do sol é aproximadamente\(10\) AU e o mais distante é aproximadamente\(30\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do planeta.

    Este gráfico mostra uma elipse com centro (0, 0), vértices (menos 20, 0) e (20, 0). O sol é mostrado no ponto (10, 0), que está a 30 unidades do vértice esquerdo e 10 unidades do vértice direito.
    Figura 11.3.60

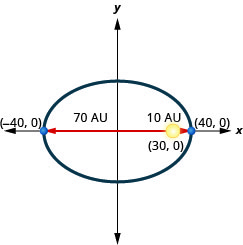
    2. Um planeta se move em uma órbita elíptica ao redor de seu sol. O mais próximo que o planeta chega do sol é aproximadamente\(10\) AU e o mais distante é aproximadamente\(70\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do planeta.

    Este gráfico mostra uma elipse com centro (0, 0), vértices (menos 40, 0) e (40, 0). O sol é mostrado no ponto (30, 0), que está a 70 unidades do vértice esquerdo e 10 unidades do vértice direito.
    Figura 11.3.61

    3. Um cometa se move em uma órbita elíptica ao redor do sol. O mais próximo que o cometa chega do sol é aproximadamente\(15\) AU e o mais distante é aproximadamente\(85\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do cometa.

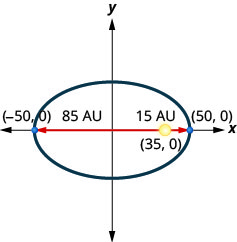
    Este gráfico mostra uma elipse com centro (0, 0), vértices (menos 50, 0) e (50, 0). O sol é mostrado no ponto (35, 0), que é 85 unidades do vértice esquerdo e 15 unidades do vértice direito.
    Figura 11.3.62

    4. Um cometa se move em uma órbita elíptica ao redor do sol. O mais próximo que o cometa chega do sol é aproximadamente\(15\) AU e o mais distante é aproximadamente\(95\) AU. O sol é um dos focos da órbita elíptica. Deixando a elipse centrar na origem e rotulando os eixos em AU, a órbita ficará parecida com a figura abaixo. Use o gráfico para escrever uma equação para a órbita elíptica do cometa.

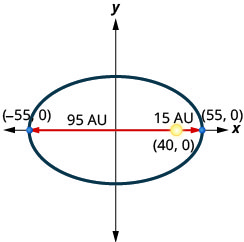
    Este gráfico mostra uma elipse com centro (0, 0), vértices (menos 55, 0) e (55, 0). O sol é mostrado no ponto (40, 0), que é 95 unidades do vértice esquerdo e 15 unidades do vértice direito.
    Figura 11.3.63
    Resposta

    1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    Exercício\(\PageIndex{22}\) Writing Exercises
    1. Com suas próprias palavras, defina uma elipse e escreva a equação de uma elipse centrada na origem na forma padrão. Desenhe um esboço da elipse rotulando o centro, os vértices e os eixos maior e menor.
    2. Explique com suas próprias palavras como obter os eixos da equação na forma padrão.
    3. Compare e contraste os gráficos das equações\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\)\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) e.
    4. Explique com suas próprias palavras, a diferença entre um vértice e um foco da elipse.
    Resposta

    1. As respostas podem variar

    3. As respostas podem variar

    Verificação automática

    a. Depois de concluir os exercícios, use esta lista de verificação para avaliar seu domínio dos objetivos desta seção.

    Esta tabela tem 4 colunas, 4 linhas e uma linha de cabeçalho. A linha do cabeçalho rotula cada coluna que eu posso, com confiança, com alguma ajuda e não, eu não entendo.™ As primeiras colunas têm as seguintes afirmações: representar graficamente uma elipse com centro na origem, encontrar a equação de uma elipse com centro na origem, representar graficamente uma elipse com centro não na origem, resolver aplicações com elipses. As colunas restantes estão em branco.
    Figura 11.3.64

    b. O que essa lista de verificação lhe diz sobre o seu domínio desta seção? Quais etapas você tomará para melhorar?