11.2: Fórmulas e círculos de distância e ponto médio
- Page ID
- 183718
Ao final desta seção, você poderá:
- Use a fórmula da distância
- Use a fórmula do ponto médio
- Escreva a equação de uma circunferência na forma padrão
- Faça um gráfico de um círculo
Antes de começar, faça este teste de prontidão.
- Encontre o comprimento da hipotenusa de um triângulo reto cujas pernas são\(12\) e\(16\) polegadas.
Se você perdeu esse problema, consulte o Exemplo 2.34. - Fator:\(x^{2}-18 x+81\).
Se você perdeu esse problema, consulte o Exemplo 6.24. - Resolva completando o quadrado:\(x^{2}-12 x-12=0\).
Se você perdeu esse problema, consulte o Exemplo 9.22.
Neste capítulo, examinaremos as seções cônicas, geralmente chamadas de cônicas, e suas propriedades. As cônicas são curvas que resultam de um plano que cruza um cone duplo — dois cones colocados ponto a ponto. Cada metade de um cone duplo é chamada de nappe.
Há quatro cônicas: o círculo, a parábola, a elipse e a hipérbole. A figura a seguir mostra como o plano que cruza o cone duplo resulta em cada curva.
Cada uma das curvas tem muitos aplicativos que afetam sua vida diária, desde seu telefone celular até sistemas de acústica e navegação. Nesta seção, veremos as propriedades de um círculo.
Use a fórmula da distância
Usamos o Teorema de Pitágoras para encontrar os comprimentos dos lados de um triângulo reto. Aqui, usaremos esse teorema novamente para encontrar distâncias no sistema de coordenadas retangulares. Ao encontrar a distância no sistema de coordenadas retangulares, podemos fazer uma conexão entre a geometria de uma cônica e a álgebra, o que abre um mundo de oportunidades de aplicação.
Nosso primeiro passo é desenvolver uma fórmula para encontrar distâncias entre pontos no sistema de coordenadas retangulares. Traçaremos os pontos e criaremos um triângulo reto da mesma forma que fizemos quando encontramos a inclinação em gráficos e funções. Em seguida, damos um passo adiante e usamos o Teorema de Pitágoras para encontrar o comprimento da hipotenusa do triângulo, que é a distância entre os pontos.
Use o sistema de coordenadas retangulares para encontrar a distância entre os pontos\((6,4)\)\((2,1)\) e.
Solução
| Faça um gráfico dos dois pontos. Conecte os dois pontos com uma linha. Desenhe um triângulo reto como se você fosse encontrar uma inclinação. |
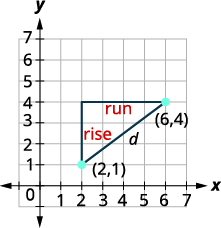
|
| Encontre o comprimento de cada perna. |
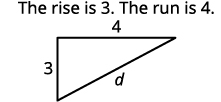
|
| Use o Teorema de Pitágoras para encontrar\(d\) a distância entre os dois pontos. | \(a^{2}+b^{2}=c^{2}\) |
| Substitua os valores. | \(3^{2}+4^{2}=d^{2}\) |
| Simplifique. | \(9+16=d^{2}\) |
| \(25=d^{2}\) | |
| Use a propriedade Square Root. | \(d=5\quad\cancel{d=-5}\) |
| Como a distância\(d\) é positiva, podemos eliminar\(d=-5\). | A distância entre os pontos\((6,4)\) e\((2,1)\) é\(5\). |
Use o sistema de coordenadas retangulares para encontrar a distância entre os pontos\((6,1)\)\((2,-2)\) e.
- Resposta
-
\(d=5\)
Use o sistema de coordenadas retangulares para encontrar a distância entre os pontos\((5,3)\)\((-3,-3)\) e.
- Resposta
-
\(d=10\)
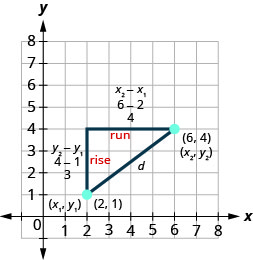
O método que usamos no último exemplo nos leva à fórmula para encontrar a distância entre os dois pontos\(\left(x_{1}, y_{1}\right)\)\(\left(x_{2}, y_{2}\right)\) e.
Quando encontramos o comprimento da perna horizontal, subtraímos\(6−2\) o que é\(x_{2}-x_{1}\).
Quando encontramos o comprimento da perna vertical, subtraímos\(4−1\) o que é\(y_{2}-y_{1}\).
Se o triângulo estivesse em uma posição diferente, poderíamos ter subtraído\(x_{1}-x_{2}\) ou\(y_{1}-y_{2}\). As expressões\(x_{2}-x_{1}\)\(x_{1}-x_{2}\) variam apenas no sinal do número resultante. Para obter o valor positivo, já que a distância é positiva, podemos usar o valor absoluto. Então, para generalizar, diremos\(\left|x_{2}-x_{1}\right|\)\(\left|y_{2}-y_{1}\right|\) e.
No Teorema de Pitágoras, substituímos as expressões gerais\(\left|x_{2}-x_{1}\right|\) e\(\left|y_{2}-y_{1}\right|\) não os números.
\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)
Esta é a fórmula de distância que usamos para encontrar a distância\(d\) entre os dois pontos\((x_{1},y_{1})\)\((x_{2}, y_{2})\) e.
Fórmula de distância
A distância\(d\) entre os dois pontos\((x_{1},y_{1})\) e\((x_{2}, y_{2})\) é
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((-5,-3)\)\((7,2)\) e.
Solução:
Escreva a fórmula da distância.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Identifique os\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\) pontos\(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) e substitua.
\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)
Simplifique.
\(d=\sqrt{12^{2}+5^{2}}\)
\(d=\sqrt{144+25}\)
\(d=\sqrt{169}\)
\(d=13\)
Resposta:
\(d=13\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((-4,-5)\)\((5,7)\) e.
- Resposta
-
\(d=15\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((-2,-5)\)\((-14,-10)\) e.
- Resposta
-
\(d=13\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((10,−4)\)\((−1,5)\) e. Escreva a resposta na forma exata e, em seguida, encontre a aproximação decimal, arredondada para o décimo mais próximo, se necessário.
Solução:
Escreva a fórmula da distância.
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Identifique os\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\) pontos\(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) e substitua.
\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)
Simplifique.
\(d=\sqrt{(-11)^{2}+9^{2}}\)
\(d=\sqrt{121+81}\)
\(d=\sqrt{202}\)
Como não\(202\) é um quadrado perfeito, podemos deixar a resposta na forma exata ou encontrar uma aproximação decimal.
\(d=\sqrt{202}\)
ou
\(d \approx 14.2\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((−4,−5)\)\((3,4)\) e. Escreva a resposta na forma exata e, em seguida, encontre a aproximação decimal, arredondada para o décimo mais próximo, se necessário.
- Resposta
-
\(d=\sqrt{130}, d \approx 11.4\)
Use a Fórmula de Distância para encontrar a distância entre os pontos\((−2,−5)\)\((−3,−4)\) e. Escreva a resposta na forma exata e, em seguida, encontre a aproximação decimal, arredondada para o décimo mais próximo, se necessário.
- Resposta
-
\(d=\sqrt{2}, d \approx 1.4\)
Use a fórmula do ponto médio
Muitas vezes, é útil ser capaz de encontrar o ponto médio de um segmento. Por exemplo, se você tiver as extremidades do diâmetro de um círculo, talvez queira encontrar o centro do círculo, que é o ponto médio do diâmetro. Para encontrar o ponto médio de um segmento de linha, encontramos a média das\(x\) coordenadas -e a média das\(y\) coordenadas -dos pontos finais.
Fórmula do ponto médio
O ponto médio do segmento de linha cujos pontos finais são os dois pontos\(\left(x_{1}, y_{1}\right)\) e\(\left(x_{2}, y_{2}\right)\) é
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Para encontrar o ponto médio de um segmento de linha, encontramos a média das\(x\) coordenadas -e a média das\(y\) coordenadas -dos pontos finais.
Use a Fórmula do Ponto Médio para encontrar o ponto médio dos segmentos de linha cujos pontos finais são\((−5,−4)\)\((7,2)\) e. Faça um gráfico das extremidades e do ponto médio em um sistema de coordenadas retangular.
Solução:
| Escreva a fórmula do ponto médio. | \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\) |
| Identifique os pontos\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-4}\end{array}\right), \left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) e substitua. | \(\left(\frac{-5+7}{2}, \frac{-4+2}{2}\right)\) |
| Simplifique. | \(\left(\frac{2}{2}, \frac{-2}{2}\right)\) |
|
\((1,-1)\) O ponto médio do segmento é o ponto \((1,-1)\). |
|
| Faça um gráfico dos pontos finais e do ponto médio. |
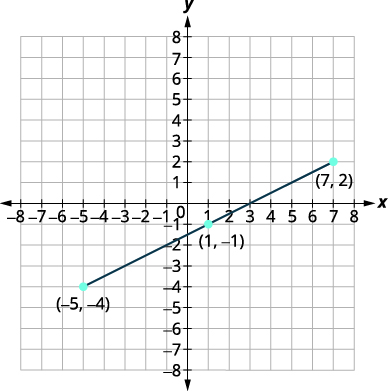
|
Use a Fórmula do Ponto Médio para encontrar o ponto médio dos segmentos de linha cujos pontos finais são\((−3,−5)\)\((5,7)\) e. Faça um gráfico das extremidades e do ponto médio em um sistema de coordenadas retangular.
- Resposta
-
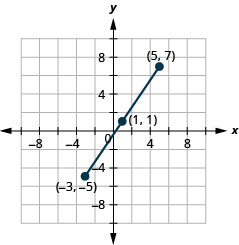
Figura 11.1.7
Use a Fórmula do Ponto Médio para encontrar o ponto médio dos segmentos de linha cujos pontos finais são\((−2,−5)\)\((6,−1)\) e. Faça um gráfico das extremidades e do ponto médio em um sistema de coordenadas retangular.
- Resposta
-
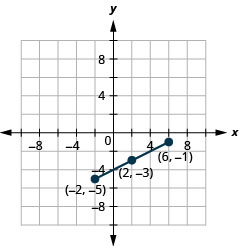
Figura 11.1.8
Tanto a Fórmula da Distância quanto a Fórmula do Ponto Médio dependem de dois pontos,\(\left(x_{1}, y_{1}\right)\)\(\left(x_{2}, y_{2}\right)\) e. É fácil confundir qual fórmula requer adição e qual subtração das coordenadas. Se nos lembrarmos de onde vêm as fórmulas, talvez seja mais fácil lembrá-las.
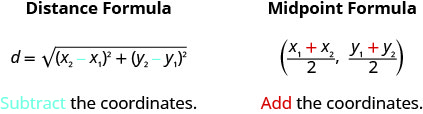
Escreva a equação de um círculo na forma padrão
Como mencionamos, nosso objetivo é conectar a geometria de uma cônica com a álgebra. Usando o plano coordenado, podemos fazer isso facilmente.
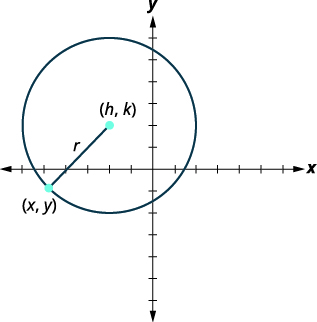
Definimos um círculo como todos os pontos em um plano que estão a uma distância fixa de um determinado ponto no plano. O ponto dado é chamado de centro\((h,k)\), e a distância fixa é chamada de raio\(r\),, do círculo.
Um círculo são todos os pontos em um plano que estão a uma distância fixa de um determinado ponto no plano. O ponto dado é chamado de centro\((h,k)\), e a distância fixa é chamada de raio\(r\),, do círculo.
Observamos um círculo no sistema de coordenadas retangulares. O raio é a distância do centro,\((h,k)\), até um ponto no círculo,\((x,y)\). |
|
| Para derivar a equação de um círculo, podemos usar a fórmula da distância com os pontos\((h,k)\)\((x,y)\) e a distância,\(r\). |
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) |
| Substitua os valores. | \(r=\sqrt{(x-h)^{2}+(y-k)^{2}}\) |
| Quadrar os dois lados. | \(r^{2}=(x-h)^{2}+(y-k)^{2}\) |
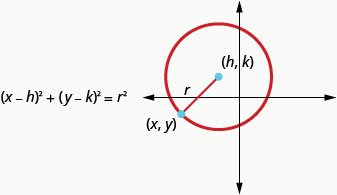
Essa é a forma padrão da equação de uma circunferência com centro\((h,k)\), e raio,\(r\).
A forma padrão da equação de uma circunferência com centro,\((h,k)\), e raio,\(r\), é
Escreva a forma padrão da equação da circunferência com raio\(3\) e centro\((0,0)\).
Solução:
| Use a forma padrão da equação de uma circunferência | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Substitua os valores\(r=3, h=0\),\(k=0\) e. | \((x-0)^{2}+(y-0)^{2}=3^{2}\) |
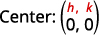 |
|
| Simplifique. | \(x^{2}+y^{2}=9\) |
Escreva a forma padrão da equação da circunferência com um raio\(6\) e um centro\((0,0)\).
- Resposta
-
\(x^{2}+y^{2}=36\)
Escreva a forma padrão da equação da circunferência com um raio\(8\) e um centro\((0,0)\).
- Responda
-
\(x^{2}+y^{2}=64\)
No último exemplo, o centro foi\((0,0)\). Observe o que aconteceu com a equação. Sempre que o centro está\((0,0)\), a forma padrão se torna\(x^{2}+y^{2}=r^{2}\).
Escreva a forma padrão da equação da circunferência com raio\(2\) e centro\((−1,3)\).
Solução:
| Use a forma padrão da equação de um círculo. | \((x-h)^{2}+(y-k)^{2}=r^{2}\) |
| Substitua os valores. | \((x-(-1))^{2}+(y-3)^{2}=2^{2}\) |
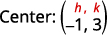 |
|
| Simplifique. | \((x+1)^{2}+(y-3)^{2}=4\) |
Escreva a forma padrão da equação da circunferência com um raio\(7\) e um centro\((2,−4)\).
- Responda
-
\((x-2)^{2}+(y+4)^{2}=49\)
Escreva a forma padrão da equação da circunferência com um raio\(9\) e um centro\((−3,−5)\).
- Responda
-
\((x+3)^{2}+(y+5)^{2}=81\)
No próximo exemplo, o raio não é fornecido. Para calcular o raio, usamos a Fórmula da Distância com os dois pontos dados.
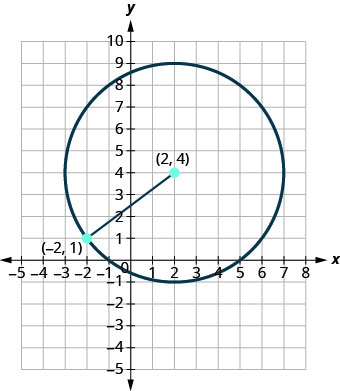
Escreva a forma padrão da equação da circunferência com centro\((2,4)\) que também contém o ponto\((−2,1)\).
Solução:
O raio é a distância do centro a qualquer ponto do círculo, então podemos usar a fórmula da distância para calculá-lo. Usaremos o centro\((2,4)\) e o ponto\((−2,1)\)
Use a Fórmula de Distância para encontrar o raio.
\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
Substitua os valores. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)
\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)
Simplifique.
\(r=\sqrt{(-4)^{2}+(-3)^{2}}\)
\(r=\sqrt{16+9}\)
\(r=\sqrt{25}\)
\(r=5\)
Agora que sabemos o raio e o centro\((2,4)\), podemos usar a forma padrão da equação de uma circunferência para encontrar a equação.\(r=5\)
Use a forma padrão da equação de um círculo.
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
Substitua os valores.
\((x-2)^{2}+(y-4)^{2}=5^{2}\)
Simplifique.
\((x-2)^{2}+(y-4)^{2}=25\)
Escreva a forma padrão da equação da circunferência com centro\((2,1)\) que também contém o ponto\((−2,−2)\).
- Responda
-
\((x-2)^{2}+(y-1)^{2}=25\)
Escreva a forma padrão da equação da circunferência com centro\((7,1)\) que também contém o ponto\((−1,−5)\).
- Responda
-
\((x-7)^{2}+(y-1)^{2}=100\)
Faça um gráfico de um círculo
Qualquer equação da forma\((x-h)^{2}+(y-k)^{2}=r^{2}\) é a forma padrão da equação de um círculo com centro\((h,k)\), e raio,\(r\). Em seguida, podemos representar graficamente o círculo em um sistema de coordenadas retangulares.
Observe que a forma padrão exige a subtração de\(x\)\(y\) e. No próximo exemplo, a equação tem\(x+2\), então precisamos reescrever a adição como subtração de um negativo.
Encontre o centro e o raio, em seguida, faça um gráfico do círculo:\((x+2)^{2}+(y-1)^{2}=9\).
Solução:
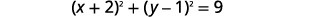 |
|
|
Use a forma padrão da equação de um círculo. Identifique o centro\((h,k)\) e o raio\(r\). |
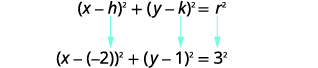 |
| Centro:\((-2,1)\) raio:\(3\) | |
| Faça um gráfico do círculo. | 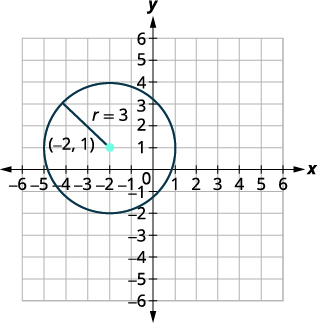 |
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\((x-3)^{2}+(y+4)^{2}=4\).
- Responda
-
- O círculo está\((3,-4)\) centrado em um raio de\(2\).
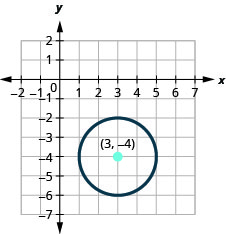
Figura 11.1.19
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\((x-3)^{2}+(y-1)^{2}=16\).
- Responda
-
- O círculo está\((3,1)\) centrado em um raio de\(4\).
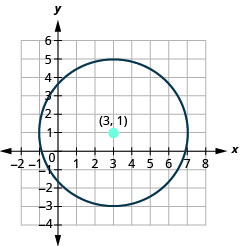
Figura 11.1.20
Para encontrar o centro e o raio, devemos escrever a equação na forma padrão. No próximo exemplo, devemos primeiro obter o coeficiente de\(x^{2}, y^{2}\) para ser um.
Encontre o centro e o raio e, em seguida, represente graficamente o círculo\(4 x^{2}+4 y^{2}=64\).
Solução:
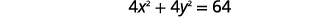 |
|
| Divida cada lado por\(4\). | 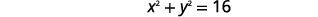 |
| Use a forma padrão da equação de um círculo. Identifique o centro\((h,k)\) e o raio\(r\). |
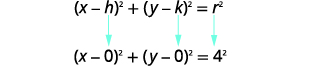 |
| Centro:\((0,0)\) raio:\(4\) | |
| Faça um gráfico do círculo. | 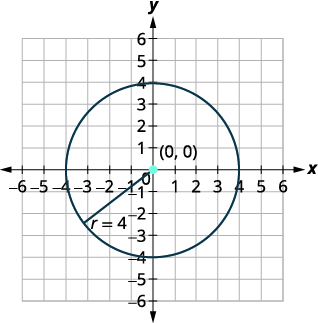 |
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(3 x^{2}+3 y^{2}=27\)
- Responda
-
- O círculo está\((0,0)\) centrado em um raio de\(3\).
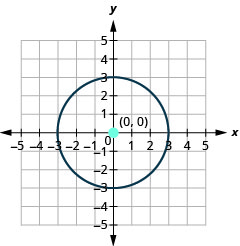
Figura 11.1.25
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(5 x^{2}+5 y^{2}=125\)
- Responda
-
- O círculo está\((0,0)\) centrado em um raio de\(5\).
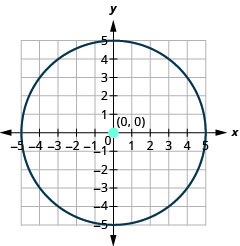
Figura 11.1.26
Se expandirmos a equação do Exemplo 11.1.8\((x+2)^{2}+(y-1)^{2}=9\), a equação do círculo parecerá muito diferente.
\((x+2)^{2}+(y-1)^{2}=9\)
Efetue o quadrado dos binômios.
\(x^{2}+4 x+4+y^{2}-2 y+1=9\)
Organize os termos em ordem decrescente de graus e obtenha zero à direita
\(x^{2}+y^{2}+4 x-2 y-4=0\)
Essa forma da equação é chamada de forma geral da equação da circunferência.
A forma geral da equação de uma circunferência é
\(x^{2}+y^{2}+a x+b y+c=0\)
Se recebermos uma equação em forma geral, podemos alterá-la para a forma padrão completando os quadrados em\(x\)\(y\) e. Em seguida, podemos representar graficamente o círculo usando seu centro e raio.
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}-4 x-6 y+4=0\)
Solução:
Precisamos reescrever essa forma geral na forma padrão para encontrar o centro e o raio.
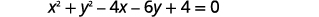
|
|
| Agrupe os\(x\) -terms e\(y\) -terms. Colete as constantes no lado direito. |
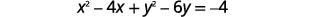
|
| Complete os quadrados. |
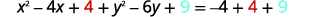
|
| Reescreva como quadrados binomiais. |
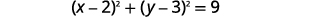
|
| Identifique o centro e o raio. | Centro:\((2,3)\) raio:\(3\) |
| Faça um gráfico do círculo. |
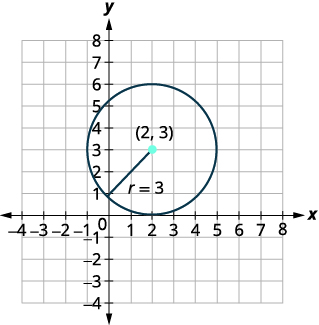
|
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}-6 x-8 y+9=0\).
- Responda
-
- O círculo está\((3,4)\) centrado em um raio de\(4\).
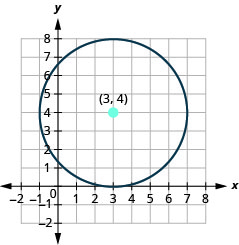
Figura 11.1.32
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}+6 x-2 y+1=0\)
- Responda
-
- O círculo está\((-3,1)\) centrado em um raio de\(3\).
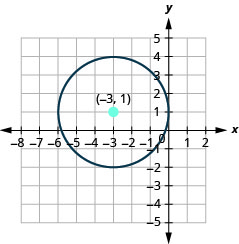
Figura 11.1.33
No próximo exemplo, há um\(y\) termo -e um\(y^{2}\) -termo. Mas observe que não há\(x\) termo -, apenas um\(x^{2}\) termo -. Já vimos isso antes e sabemos que isso significa que\(h\) é\(0\). Precisaremos preencher o quadrado para os\(y\) termos, mas não para os\(x\) termos.
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}+8 y=0\)
Solução:
Precisamos reescrever essa forma geral na forma padrão para encontrar o centro e o raio.
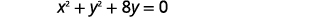 |
|
| Agrupe os\(x\) -terms e\(y\) -terms. | 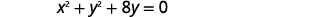 |
| Não há constantes para coletar no lado direito. | |
| Complete o quadrado para\(y^{2}+8y\). | 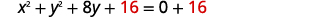 |
| Reescreva como quadrados binomiais. | 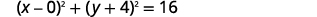 |
| Identifique o centro e o raio. | Centro:\((0,-4)\) raio:\(4\) |
| Faça um gráfico do círculo. | 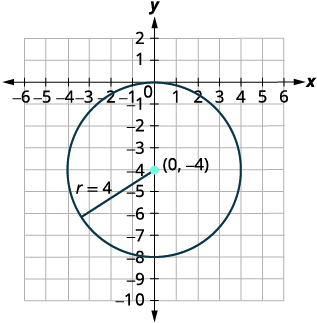 |
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}-2 x-3=0\).
- Responda
-
- O círculo está\((-1,0)\) centrado em um raio de\(2\).
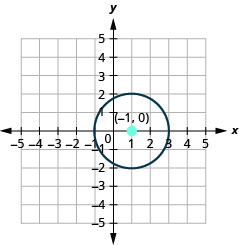
Figura 11.1.39
- Encontre o centro e o raio e, em seguida,
- Faça um gráfico do círculo:\(x^{2}+y^{2}-12 y+11=0\).
- Responda
-
- O círculo está\((0,6)\) centrado em um raio de\(5\).
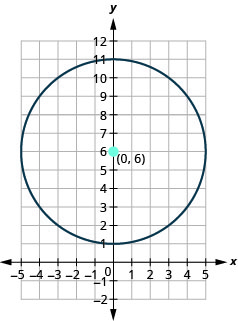
Figura 11.1.40
Acesse esses recursos on-line para obter instruções adicionais e praticar o uso de fórmulas de distância e ponto médio e criar gráficos de círculos.
- Fórmulas e círculos de distância e ponto médio
- Encontrando a distância e o ponto médio entre dois pontos
- Completando o quadrado para escrever a equação na forma padrão de um círculo
Conceitos chave
- Fórmula de distância: A distância\(d\) entre os dois pontos\(\left(x_{1}, y_{1}\right)\) e\(\left(x_{2}, y_{2}\right)\) é
\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
- Fórmula do ponto médio: O ponto médio do segmento de linha cujos pontos finais são os dois pontos\(\left(x_{1}, y_{1}\right)\) e\(\left(x_{2}, y_{2}\right)\) é
\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Para encontrar o ponto médio de um segmento de linha, encontramos a média das\(x\) coordenadas -e a média das\(y\) coordenadas -dos pontos finais. - Círculo: Um círculo são todos os pontos em um plano que estão a uma distância fixa de um ponto fixo no plano. O ponto dado é chamado de centro\((h,k)\), e a distância fixa é chamada de raio\(r\),, do círculo.
- Forma padrão da equação de um círculo: A forma padrão da equação de um círculo com centro,\((h,k)\), e raio,\(r\), é
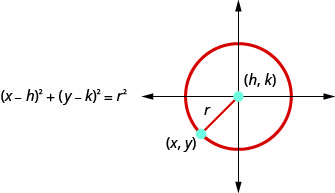
- Forma geral da equação de uma circunferência: A forma geral da equação de uma circunferência é
\(x^{2}+y^{2}+a x+b y+c=0\)
Glossário
- círculo
- Um círculo são todos os pontos em um plano que estão a uma distância fixa de um ponto fixo no plano.


