Skip to main content
Global

9.5: Resolver equações quadráticas na forma quadrática

  1. Last updated
  2. Save as PDF
  • Page ID
    183532

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Objetivos de

    Ao final desta seção, você poderá:

    • Resolva equações em forma quadrática
    Antes de começar

    ... faça este teste de prontidão.

    1. Fator por substituição:\(y^{4}-y^{2}-20\).
    2. Fator por substituição:\((y-4)^{2}+8(y-4)+15\).
    3. Simplifique
      1. \(x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}\)
      2. \(\left(x^{\frac{1}{3}}\right)^{2}\)
      3. \(\left(x^{-1}\right)^{2}\)

    Resolver equações na forma quadrática

    Às vezes, quando fatoramos os trinômios, o trinômio não parecia estar na\(ax^{2}+bx+c\) forma. Então, fatoramos por substituição, o que nos permite ajustá-la ao\(ax^{2}+bx+c\) formulário. Usamos o padrão\(u\) para a substituição.

    Para fatorar a expressão\(x^{4}-4 x^{2}-5\), notamos que a parte variável do termo médio é\(x^{2}\) e seu quadrado\(x^{4}\),, é a parte variável do primeiro termo. (Nós sabemos\(\left(x^{2}\right)^{2}=x^{4}\).) Então, deixamos\(u=x^{2}\) e fatoramos.

      \(x^{4}-4 x^{2}-5\)
      \(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\)
    Deixe\(u=x^{2}\) e substitua. \(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\)
    Considere o trinômio. \((u+1)(u-5)\)
    \(u\)Substitua por\(x^{2}\). \(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\)

    Da mesma forma, às vezes uma equação não está na\(ax^{2}+bx+c=0\) forma, mas se parece muito com uma equação quadrática. Então, muitas vezes podemos fazer uma substituição cuidadosa que nos permitirá ajustá-la ao\(ax^{2}+bx+c=0\) formulário. Se conseguirmos ajustá-lo à forma, poderemos usar todos os nossos métodos para resolver equações quadráticas.

    Observe que na equação quadrática\(ax^{2}+bx+c=0\), o termo intermediário tem uma variável\(x\),, e seu quadrado\(x^{2}\),, é a parte variável do primeiro termo. Procure esse relacionamento ao tentar encontrar um substituto.

    Novamente, usaremos o padrão\(u\) para fazer uma substituição que colocará a equação na forma quadrática. Se a substituição nos der uma equação da forma\(ax^{2}+bx+c=0\), dizemos que a equação original era de forma quadrática.

    O próximo exemplo mostra as etapas para resolver uma equação na forma quadrática.

    Exemplo\(\PageIndex{1}\) How to Solve Equations in Quadratic Form

    Resolver:\(6 x^{4}-7 x^{2}+2=0\)

    Solução:

    Etapa 1: Identifique uma substituição que colocará a equação na forma quadrática. Desde então\(\left(x^{2}\right)^{2}=x^{4}\), deixamos\(u=x^{2}\). \(6 x^{4}-7 x^{2}+2=0\)
    Etapa 2: Reescreva a equação com a substituição para colocá-la na forma quadrática.

    Reescreva para se preparar para a substituição.

    Substituto\(u=x^{2}\).

    		 \(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\)
    Etapa 3: Resolva a equação quadrática para\(u\).

    Podemos resolver fatorando.

    Use a propriedade Zero Product.

    		 \(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\)
    Etapa 4: Substitua a variável original novamente nos resultados, usando a substituição. \(u\)Substitua por\(x^{2}\). \(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\)
    Etapa 5: resolva a variável original. Resolva para\(x\), usando a propriedade de raiz quadrada.

    \(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\)

    Existem quatro soluções.

    \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\)
    Etapa 6: verifique as soluções. Verifique todas as quatro soluções. Mostraremos um cheque aqui.

    \(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\)

    Deixamos os outros cheques para você!
    Exercício\(\PageIndex{1}\)

    Resolver:\(x^{4}-6 x^{2}+8=0\).

    Resposta

    \(x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2\)

    Exercício\(\PageIndex{2}\)

    Resolver:\(x^{4}-11 x^{2}+28=0\).

    Resposta

    \(x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2\)

    Resumimos as etapas para resolver uma equação na forma quadrática.

    Resolver equações na forma quadrática
    1. Identifique uma substituição que colocará a equação na forma quadrática.
    2. Reescreva a equação com a substituição para colocá-la na forma quadrática.
    3. Resolva a equação quadrática para\(u\).
    4. Substitua a variável original novamente nos resultados, usando a substituição.
    5. Resolva a variável original.
    6. Verifique as soluções.

    No exemplo a seguir, o binômio no termo médio\((x-2)\) é quadrado no primeiro termo. Se deixarmos\(u=x-2\) e substituirmos, nosso trinômio estará em\(a x^{2}+b x+c\) forma.

    Exemplo\(\PageIndex{2}\)

    Resolver:\((x-2)^{2}+7(x-2)+12=0\).

    Solução:

      \((x-2)^{2}+7(x-2)+12=0\)
    Prepare-se para a substituição. \(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\)
    Deixe\(u=x-2\) e substitua. \(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\)
    Resolva por fatoração.

    \((u+3)(u+4)=0\)

    \ (\ begin {reunido}
    u+3=0,\ quad u+4=0\\
    u=-3,\ quad u=-4
    \ end {reunido}\)

    \(u\)Substitua por\(x-2\).

    \(x-2=-3, \quad x-2=-4\)

    Resolva para\(x\).

    \(x=-1, \quad x=-2\)

    Confira: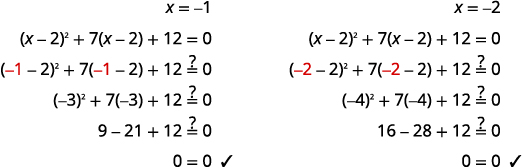

    .
    Figura 9.4.14
    		  
    Exercício\(\PageIndex{3}\)

    Resolver:\((x-5)^{2}+6(x-5)+8=0\).

    Resposta

    \(x=3, x=1\)

    Exercício\(\PageIndex{4}\)

    Resolver:\((y-4)^{2}+8(y-4)+15=0\).

    Resposta

    \(y=-1, y=1\)

    No exemplo a seguir, notamos isso\((\sqrt{x})^{2}=x\). Além disso, lembre-se de que quando quadramos os dois lados de uma equação, podemos introduzir raízes estranhas. Certifique-se de verificar suas respostas!

    Exemplo\(\PageIndex{3}\)

    Resolver:\(x-3 \sqrt{x}+2=0\).

    Solução:

    O,\(\sqrt{x}\) no médio prazo, é quadrado no primeiro termo\((\sqrt{x})^{2}=x\). Se deixarmos\(u=\sqrt{x}\) e substituirmos, nosso trinômio estará em\(a x^{2}+b x+c=0\) forma.

      \(x-3 \sqrt{x}+2=0\)
    Reescreva o trinômio para se preparar para a substituição. .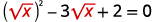
    Deixe\(u=\sqrt{x}\) e substitua. .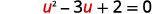
    Resolva por fatoração.

    \((u-2)(u-1)=0\)

    \(u-2=0, \quad u-1=0\)
    \(u=2, \quad u=1\)\)
    \(u\)Substitua por\(\sqrt{x}\).

    \(\sqrt{x}=2, \quad \sqrt{x}=1\)
    Resolva por\(x\), quadrando os dois lados. \(x=4, \quad x=1\)

    Confira: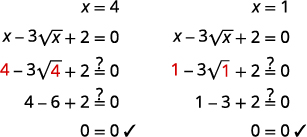

    .
    		  
    Exercício\(\PageIndex{5}\)

    Resolver:\(x-7 \sqrt{x}+12=0\).

    Resposta

    \(x=9, x=16\)

    Exercício\(\PageIndex{6}\)

    Resolver:\(x-6 \sqrt{x}+8=0\).

    Resposta

    \(x=4, x=16\)

    Substituições por expoentes racionais também podem nos ajudar a resolver uma equação na forma quadrática. Pense nas propriedades dos expoentes ao começar o próximo exemplo.

    Exemplo\(\PageIndex{4}\)

    Resolver:\(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\).

    Solução:

    O\(x^{\frac{1}{3}}\) termo intermediário é quadrado no primeiro termo\(\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}\). Se deixarmos\(u=x^{\frac{1}{3}}\) e substituirmos, nosso trinômio estará em\(a x^{2}+b x+c=0\) forma.

      \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\)
    Reescreva o trinômio para se preparar para a substituição. .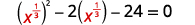
    Deixe\(u=x^{\frac{1}{3}}\) .
    Resolva por fatoração.

    \((u-6)(u+4)=0\)

    \(u-6=0, \quad u+4=0\)

    \(u=6, \quad u=-4\)
    \(u\)Substitua por\(x^{\frac{1}{3}}\).

    \(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\)
    Resolva o problema\(x\) cortando os dois lados.

    \(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\)

    \(x=216, \quad x=-64\)

    Confira: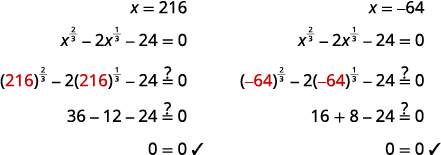

    .
    Figura 9.4.33
    		  
    Exercício\(\PageIndex{7}\)

    Resolver:\(x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0\).

    Resposta

    \(x=-8, x=343\)

    Exercício\(\PageIndex{8}\)

    Resolver:\(x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0\).

    Resposta

    \(x=81, x=625\)

    No próximo exemplo, precisamos ter em mente a definição de um expoente negativo, bem como as propriedades dos expoentes.

    Exemplo\(\PageIndex{5}\)

    Resolver:\(3 x^{-2}-7 x^{-1}+2=0\).

    Solução:

    O\(x^{−1}\) termo intermediário é quadrado no primeiro termo\(\left(x^{-1}\right)^{2}=x^{-2}\). Se deixarmos\(u=x^{−1}\) e substituirmos, nosso trinômio estará em\(a x^{2}+b x+c=0\) forma.

      \(3 x^{-2}-7 x^{-1}+2=0\)
    Reescreva o trinômio para se preparar para a substituição. .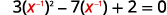
    Deixe\(u=x^{-1}\) e substitua. .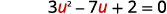
    Resolva por fatoração. \((3 u-1)(u-2)=0\)
      \(3 u-1=0, \quad u-2=0\)
      \(u=\frac{1}{3}, \quad u=2\)
    \(u\)Substitua por\(x^{-1}\). \(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\)
    Resolva\(x\) por meio do recíproco desde então\(x^{-1}=\frac{1}{x}\). \(x=3, \quad x=\frac{1}{2}\)

    Confira: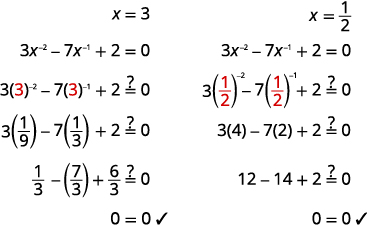

    .
    Figura 9.4.42
    		  
    Exercício\(\PageIndex{9}\)

    Resolver:\(8 x^{-2}-10 x^{-1}+3=0\).

    Resposta

    \(x=\frac{4}{3}, x=2\)

    Exercício\(\PageIndex{10}\)

    Resolver:\(6 x^{-2}-23 x^{-1}+20=0\).

    Resposta

    \(x=\frac{2}{5}, x=\frac{3}{4}\)

    Acesse este vídeo on-line para obter instruções e práticas adicionais na resolução de equações quadráticas: https://www.youtube.com/watch?v=7X-CZMbpxuw

    Conceitos-chave

    • Como resolver equações na forma quadrática.
      1. Identifique uma substituição que colocará a equação na forma quadrática.
      2. Reescreva a equação com a substituição para colocá-la na forma quadrática.
      3. Resolva a equação quadrática para\(u\).
      4. Substitua a variável original novamente nos resultados, usando a substituição.
      5. Resolva a variável original.
      6. Verifique as soluções.