7.7: Resolver desigualdades racionais
- Page ID
- 183663
- Resolva desigualdades racionais
- Resolva uma desigualdade com funções racionais
Antes de começar, faça este teste de prontidão.
- Encontre o valor de\(x-5\) when ⓐ\(x=6\) ⓑ\(x=-3\) ⓒ\(x=5\)
Se você perdeu esse problema, consulte o Exemplo 1.2.16. - Solução:\(8-2 x<12\)
Se você perdeu esse problema, consulte o Exemplo 2.6.13. - Escreva em notação de intervalo:\(-3 \leq x<5 \)
Se você perdeu esse problema, consulte o Exemplo 2.6.4.
Resolva desigualdades racionais
Aprendemos a resolver desigualdades lineares depois de aprender a resolver equações lineares. As técnicas eram praticamente as mesmas, com uma grande exceção. Quando multiplicamos ou dividimos por um número negativo, o sinal de desigualdade se inverteu.
Tendo acabado de aprender a resolver equações racionais, agora estamos prontos para resolver desigualdades racionais. Uma desigualdade racional é uma desigualdade que contém uma expressão racional.
Uma desigualdade racional é uma desigualdade que contém uma expressão racional.
Desigualdades como\(\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad\) e\(\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad \) são desigualdades racionais, pois cada uma contém uma expressão racional.
Quando resolvemos uma desigualdade racional, usaremos muitas das técnicas que usamos para resolver desigualdades lineares. Devemos lembrar especialmente que quando multiplicamos ou dividimos por um número negativo, o sinal de desigualdade deve ser revertido.
Outra diferença é que devemos considerar cuidadosamente qual valor pode tornar a expressão racional indefinida e, portanto, deve ser excluído.
Quando resolvemos uma equação e o resultado é\(x=3\), sabemos que há uma solução, que é 3.
Quando resolvemos uma desigualdade e o resultado é\(x>3\), sabemos que existem muitas soluções. Representamos graficamente o resultado para ajudar a mostrar melhor todas as soluções e começamos com 3. Três se torna um ponto crítico e então decidimos se devemos sombrear à esquerda ou à direita dele. Os números à direita de 3 são maiores que 3, então sombreamos para a direita.

Para resolver uma desigualdade racional, primeiro devemos escrever a desigualdade com apenas um quociente à esquerda e 0 à direita.
Em seguida, determinamos os pontos críticos a serem usados para dividir a reta numérica em intervalos. Um ponto crítico é um número que torna a expressão racional zero ou indefinida.
Em seguida, avaliaremos os fatores do numerador e do denominador e encontraremos o quociente em cada intervalo. Isso identificará o intervalo, ou intervalos, que contém todas as soluções da desigualdade racional.
Escrevemos a solução em notação de intervalo tomando cuidado para determinar se os pontos finais estão incluídos.
Resolva e escreva a solução em notação de intervalo:\(\dfrac{x-1}{x+3} \geq 0\)
Solução
Etapa 1. Escreva a desigualdade como um quociente à esquerda e zero à direita.
Nossa desigualdade está nessa forma. \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Etapa 2. Determine os pontos críticos — os pontos em que a expressão racional será zero ou indefinida.
A expressão racional será zero quando o numerador for zero. Desde\(x-1=0\) quando\(x=1\), então 1 é um ponto crítico.
A expressão racional será indefinida quando o denominador for zero. Desde\(x+3=0\) quando\(x=-3\), -3 é um ponto crítico.
Os pontos críticos são 1 e -3.
Etapa 3. Use os pontos críticos para dividir a reta numérica em intervalos.
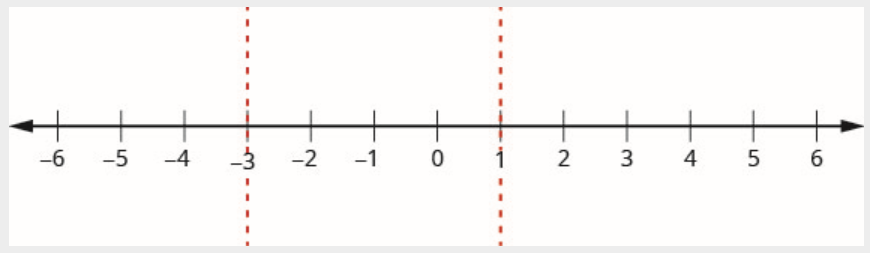
A reta numérica é dividida em três intervalos:
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]
Etapa 4. Teste um valor em cada intervalo. Acima da linha numérica, mostre o sinal de cada fator da expressão racional em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.
Para encontrar o sinal de cada fator em um intervalo, escolhemos qualquer ponto nesse intervalo e o usamos como ponto de teste. Qualquer ponto no intervalo dará à expressão o mesmo sinal, então podemos escolher qualquer ponto no intervalo.
\[\text { Interval }(-\infty,-3) \nonumber \]
O número -4 está no intervalo\((-\infty,-3)\). Teste\(x=-4\) na expressão no numerador e no denominador.
O numerador:
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]
O denominador:
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Acima da linha numérica, marque o fator\(x-1\) negativo e marque o fator\(x+3\) negativo.
Como um negativo dividido por um negativo é positivo, marque o quociente positivo no intervalo\((-\infty,-3)\)
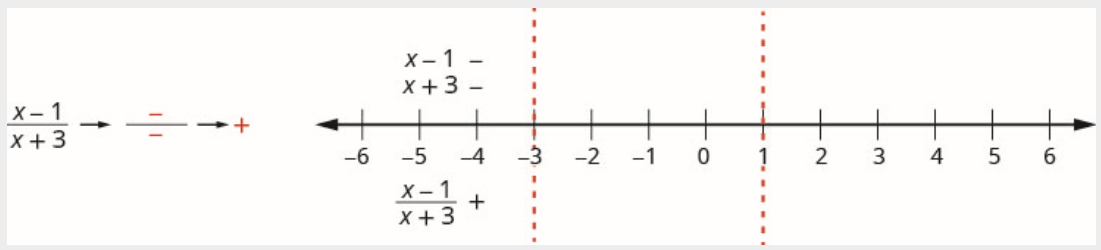
\[\text {Interval } (-3,1) \nonumber \]
O número 0 está no intervalo\((-3,1)\). Teste\(x=0\).
O numerador:
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
O denominador:
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]
Acima da linha numérica, marque o fator\(x-1\) negativo e marque\(x+3\) positivo.
Como um negativo dividido por um positivo é negativo, o quociente é marcado como negativo no intervalo\((-3,1)\).
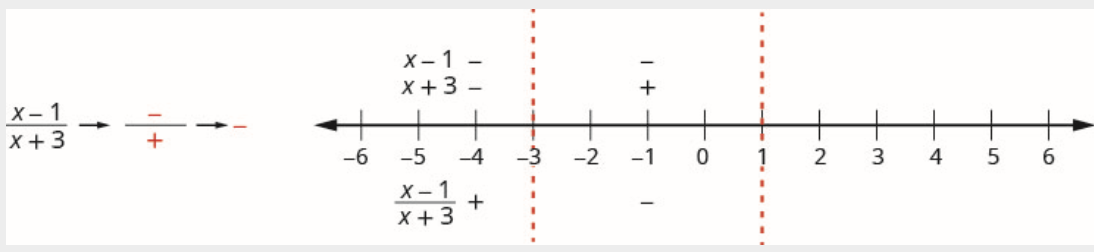
\[\text {Interval }(1, \infty) \nonumber \]
O número 2 está no intervalo\((1, \infty)\). Teste\(x=2\).
O numerador:
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
O denominador:
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]
Acima da linha numérica, marque o fator\(x-1\) positivo e marque\(x+3\) positivo.
Como um positivo dividido por um positivo é positivo, marque o quociente positivo no intervalo\((1, \infty)\).
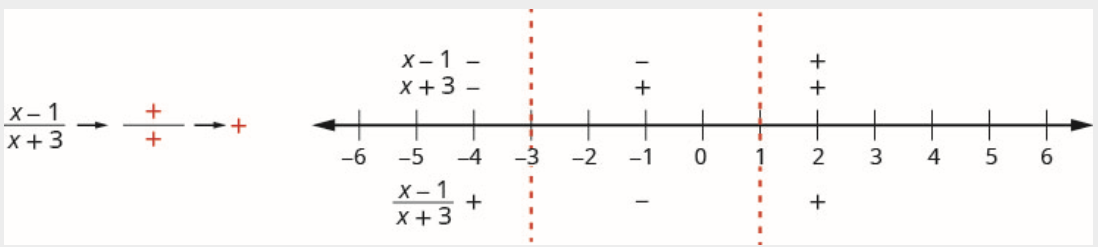
Etapa 5. Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.
Queremos que o quociente seja maior ou igual a zero, então os números nos intervalos\((-\infty,-3)\)\((1, \infty) \) são soluções.
Mas e os pontos críticos?
O ponto crítico\(x=-3\) torna o denominador 0, então ele deve ser excluído da solução e nós o marcamos com um parêntese.
O ponto crítico\(x=1\) torna toda a expressão racional 0. A desigualdade exige que a expressão racional seja maior ou igual a. Então, 1 faz parte da solução e vamos marcá-lo com um colchete.
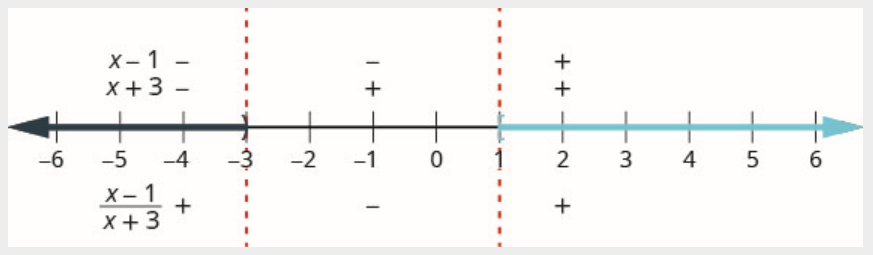
Lembre-se de que quando temos uma solução composta por mais de um intervalo, usamos o símbolo de união\(\cup \),, para conectar os dois intervalos. A solução na notação de intervalo é\((-\infty,-3) \cup[1, \infty)\).
Resolva e escreva a solução em notação de intervalo:\(\dfrac{x-2}{x+4} \geq 0\)
- Resposta
-
\((-\infty,-4) \cup[2, \infty)\)
Resolva e escreva a solução em notação de intervalo:\(\dfrac{x+2}{x-4} \geq 0\)
- Resposta
-
\((-\infty,-2] \cup(4, \infty)\)
Resumimos as etapas para facilitar a referência.
Etapa 1. Escreva a desigualdade como um quociente à esquerda e zero à direita.
Etapa 2. Determine os pontos críticos — os pontos em que a expressão racional será zero ou indefinida.
Etapa 3. Use os pontos críticos para dividir a reta numérica em intervalos.
Etapa 4. Teste um valor em cada intervalo. Acima da linha numérica, mostre o sinal de cada fator do numerador e do denominador em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.
Etapa 5. Determine os intervalos em que a desigualdade está correta. Escreva a solução em notação de intervalo.
O próximo exemplo exige que primeiro coloquemos a desigualdade racional na forma correta.
Resolva e escreva a solução em notação de intervalo:\(\dfrac{4 x}{x-6}<1\)
Solução
\[\dfrac{4 x}{x-6}<1 \nonumber \]
Subtraia 1 para obter zero à direita.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Reescreva 1 como uma fração usando o LCD.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Subtraia os numeradores e coloque a diferença sobre o denominador comum.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Simplifique.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Fator o numerador para mostrar todos os fatores.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Encontre os pontos críticos.
O quociente será zero quando o numerador for zero. O quociente é indefinido quando o denominador é zero.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]
Use os pontos críticos para dividir a reta numérica em intervalos.
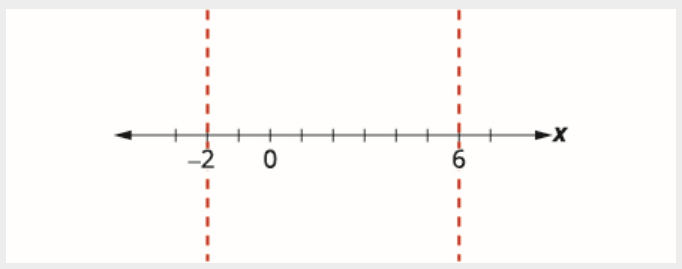
Teste um valor em cada intervalo.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(x+2)\) | \ (-\ infty, -2)\)” style="vertical-align:middle;” class="lt-math-5164">
x+2 -3+2 -1 - |
\ (-2,6)\)” style="alinhamento vertical: médio;” class="lt-math-5164">
x+2 0+2 2 + |
\ (6,\ infty)\)” style="alinhamento vertical: médio;” class="lt-math-5164">
x+2 7+2 9 + |
| \(x-6\) | \ (-\ infty, -2)\)” style="vertical-align:middle;” class="lt-math-5164">
x-6 -3-6 -9 - |
\ (-2,6)\)” style="alinhamento vertical: médio;” class="lt-math-5164">
x-6 0-6 -6 - |
\ (6,\ infty)\)” style="alinhamento vertical: médio;” class="lt-math-5164">
x-6 7-6 1 + |
Acima da linha numérica, mostre o sinal de cada fator da expressão racional em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.
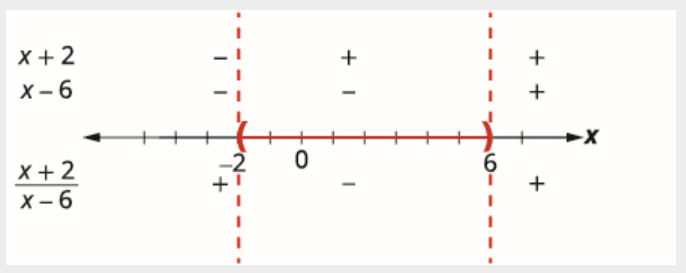
Determine os intervalos em que a desigualdade está correta. Queremos que o quociente seja negativo, então a solução inclui os pontos entre −2 e 6. Como a desigualdade é estritamente menor que, os pontos finais não são incluídos.
Escrevemos a solução em notação de intervalo como (−2, 6).
Resolva e escreva a solução em notação de intervalo:\(\dfrac{3 x}{x-3}<1\).
- Resposta
-
\(\left(-\dfrac{3}{2}, 3\right)\)
Resolva e escreva a solução em notação de intervalo:\(\dfrac{3 x}{x-4}<2\).
- Resposta
-
\((-8,4)\)
No próximo exemplo, o numerador é sempre positivo, então o sinal da expressão racional depende do sinal do denominador.
Resolva e escreva a solução em notação de intervalo:\(\dfrac{5}{x^{2}-2 x-15}>0\).
Solução
A desigualdade está na forma correta.
\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]
Fator o denominador.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Encontre os pontos críticos. O quociente é 0 quando o numerador é 0. Como o numerador é sempre 5, o quociente não pode ser 0.
O quociente será indefinido quando o denominador for zero.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Use os pontos críticos para dividir a reta numérica em intervalos.
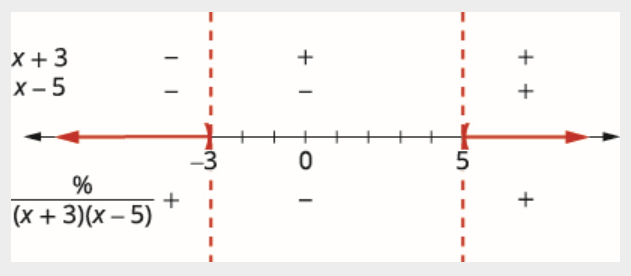
Valores de teste em cada intervalo. Acima da linha numérica, mostre o sinal de cada fator do denominador em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.
Escreva a solução em notação de intervalo.
\[(-\infty,-3) \cup(5, \infty) \nonumber \]
Solve and write the solution in interval notation: \(\dfrac{1}{x^{2}+2 x-8}>0\).
- Answer
-
\((-\infty,-4) \cup(2, \infty)\)
Solve and write the solution in interval notation: \(\dfrac{3}{x^{2}+x-12}>0 \).
- Answer
-
\((-\infty,-4) \cup(3, \infty)\)
The next example requires some work to get it into the needed form.
Solve and write the solution in interval notation: \(\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}\).
Solution
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]
Subtract \(\dfrac{5}{3 x}\) to get zero on the right.
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]
Rewrite to get each fraction with the LCD
\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]
Simplify.
\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]
Subtract the numerators and place the difference over the common denominator.
\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]
Factor the numerator.
\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]
Find the critical points.
\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]
Use the critical points to divide the number line into intervals.
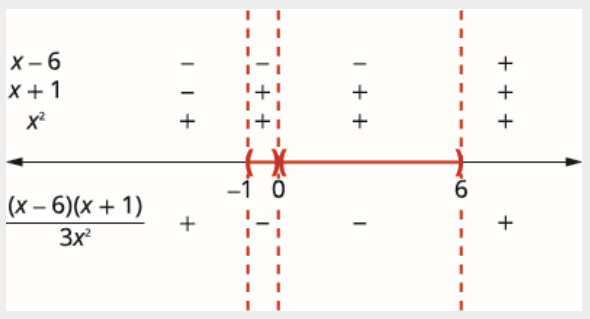
Acima da linha numérica, mostre o sinal de cada fator em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente.
Como 0 é excluído, a solução são os dois\((-1,0) \cup(0,6)\) intervalos\((-1,0)\)\((0,6)\) e.
Resolva e escreva a solução em notação de intervalo:\(\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}\).
- Resposta
-
\((2,4)\)
Resolva e escreva a solução em notação de intervalo:\(\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}\).
- Resposta
-
\((3,6)\)
Resolva uma desigualdade com funções racionais
Ao trabalhar com funções racionais, às vezes é útil saber quando a função é maior ou menor que um valor específico. Isso leva a uma desigualdade racional.
Dada a função\(R(x)=\dfrac{x+3}{x-5}\), encontre os valores de x que tornam a função menor ou igual a 0.
Solução
Queremos que a função seja menor ou igual a 0.
\[R(x) \leq 0 \nonumber \]
Substitua a expressão racional por\(R(x)\).
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Encontre os pontos críticos.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Use os pontos críticos para dividir a reta numérica em intervalos.
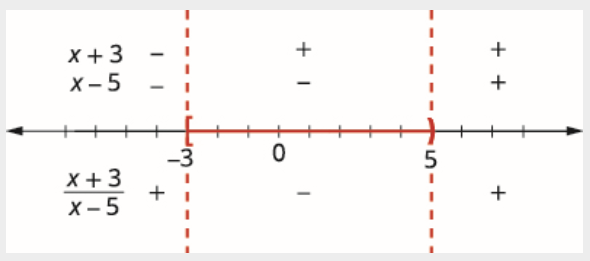
Valores de teste em cada intervalo. Acima da linha numérica, mostre o sinal de cada fator em cada intervalo. Abaixo da linha numérica, mostre o sinal do quociente. Escreva a solução em notação de intervalo. Como 5 está excluído, nós não o incluímos no intervalo.
\[[-3,5) \nonumber \]
Given the function \(R(x)=\dfrac{x-2}{x+4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\((-4,2]\)
Given the function \(R(x)=\dfrac{x+1}{x-4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\([-1,4)\)
In economics, the function \(C(x)\) is used to represent the cost of producing \(x\) units of a commodity. The average cost per unit can be found by dividing \(C(x)\) by the number of items \(x\). Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).
The function\(C(x)=10 x+3000\) represents the cost to produce \(x\), number of items. Find:
- The average cost function, \(c(x)\)
- How many items should be produced so that the average cost is less than $40.
Solution
- \[C(x)=10 x+3000 \nonumber \]
The average cost function is \(c(x)=\dfrac{C(x)}{x})\). To find the average cost function, divide the cost function by \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
The average cost function is \(c(x)=\dfrac{10 x+3000}{x} \)
- We want the function \(c(x)\) to be less than 40.
\[c(x)<40 \nonumber \]
Substitute the rational expression forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Subtract 40 to get 0 on the right.
\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]
Rewrite the left side as one quotient by finding the LCD and performing the subtraction.
\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]
Factor the numerator to show all factors.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]
Find the critical points.
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
More than 100 items must be produced to keep the average cost below $40 per item.
The function\(C(x)=20 x+6000\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $60.
- Answer
-
- \(c(x)=\dfrac{20 x+6000}{x}\)
- More than 150 items must be produced to keep the average cost below $60 per item.
The function\(C(x)=5 x+900\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $20.
- Answer
-
- \(c(x)=\dfrac{5 x+900}{x}\)
- More than 60 items must be produced to keep the average cost below $20 per item.


