6.4: Factor Special Products
- Page ID
- 183348
Ao final desta seção, você poderá:
- Fator trinômios quadrados perfeitos
- Diferenças fatoriais dos quadrados
- Somas fatoriais e diferenças dos cubos
Antes de começar, faça este teste de prontidão.
- Simplifique:\((3x^2)^3\).
- Multiplique:\((m+4)^2\).
- Multiplique:\((x−3)(x+3)\).
Vimos que alguns binômios e trinômios resultam de produtos especiais — quadrando binômios e multiplicando conjugados. Se você aprender a reconhecer esses tipos de polinômios, poderá usar os padrões de produtos especiais para fatorá-los muito mais rapidamente.
Trinômios Quadrados do Fator Perfect
Alguns trinômios são quadrados perfeitos. Eles resultam da multiplicação de um binômio pelo próprio. Nós colocamos um binômio ao quadrado usando o padrão de quadrados binomiais em um capítulo anterior.
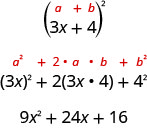
O trinômio\(9x^2+24x+16\) é chamado de trinômio quadrado perfeito. É o quadrado do binômio\(3x+4\).
Neste capítulo, você começará com um trinômio quadrado perfeito e o incluirá em seus fatores primos. Você pode fatorar esse trinômio usando os métodos descritos na última seção, pois é da forma\(ax^2+bx+c\). Mas se você reconhecer que o primeiro e o último termos são quadrados e o trinômio se encaixa no padrão perfeito de trinômios quadrados, você economizará muito trabalho. Aqui está o padrão—o inverso do padrão de quadrados binomiais.
Se\(a\) e\(b\) forem números reais
\[a^2+2ab+b^2=(a+b)^2\nonumber\]
\[a^2−2ab+b^2=(a−b)^2\nonumber\]
Para fazer uso desse padrão, você precisa reconhecer que um determinado trinômio se encaixa nele. Verifique primeiro se o coeficiente inicial é um quadrado perfeito,\(a^2\). Em seguida, verifique se o último termo é um quadrado perfeito,\(b^2\). Em seguida, verifique o prazo intermediário — é o produto\(2ab\)? Se tudo estiver certo, você poderá escrever facilmente os fatores.
Fator:\(9x^2+12x+4\).
- Resposta
-



Fator:\(4x^2+12x+9\).
- Resposta
-
\((2x+3)^2\)
Fator:\(9y^2+24y+16\).
- Resposta
-
\((3y+4)^2\)
O sinal do termo intermediário determina qual padrão usaremos. Quando o termo intermediário é negativo, usamos o padrão\(a^2−2ab+b^2\), que leva em consideração\((a−b)^2\).
As etapas estão resumidas aqui.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\)
Vamos trabalhar agora em um em que o termo médio seja negativo.
Fator:\(81y^2−72y+16\).
- Resposta
-
O primeiro e o último termos são quadrados. Veja se o termo intermediário se encaixa no padrão de um trinômio quadrado perfeito. O termo médio é negativo, então o quadrado binomial seria\((a−b)^2\).
\(81 y^{2}-72 y+16\) O primeiro e o último termo são quadrados perfeitos? 
Verifique o médio prazo. 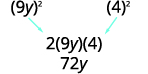
Isso combina\((a−b)^2\)? Sim. 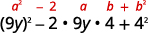
Escreva como o quadrado de um binômio. \((9 y-4)^{2}\) Verifique multiplicando:
\[(9y−4)^2\nonumber\]\[(9y)^2−2·9y·4+4^2\nonumber\]\[81y^2−72y+16\checkmark\nonumber\]
Fator:\(64y^2−80y+25\).
- Resposta
-
\((8y−5)^2\)
Fator:\(16z^2−72z+81\).
- Resposta
-
\((4z−9)^2\)
O próximo exemplo será um trinômio quadrado perfeito com duas variáveis.
Fator:\(36x^2+84xy+49y^2\).
- Resposta
-
\(36 x^{2}+84 x y+49 y^{2}\) Teste cada termo para verificar o padrão. 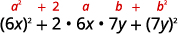
Fator. \((6 x+7 y)^{2}\) Verifique multiplicando.
\[(6x+7y)^2\nonumber\]\[(6x)^2+2·6x·7y+(7y)^2\nonumber\]\[36x^2+84xy+49y^2\checkmark\nonumber\]
Fator:\(49x^2+84xy+36y^2\).
- Resposta
-
\((7x+6y)^2\)
Fator:\(64m^2+112mn+49n^2\).
- Resposta
-
\((8m+7n)^2\)
Lembre-se de que o primeiro passo na fatoração é procurar o maior fator comum. Trinômios quadrados perfeitos podem ter um GCF em todos os três termos e devem ser considerados primeiro. E, às vezes, uma vez que o GCF tenha sido fatorado, você reconhecerá um trinômio quadrado perfeito.
Fator:\(100x^2y−80xy+16y\).
- Resposta
-
\(100 x^{2} y-80 x y+16 y\) Existe um GCF? Sim\(4y\), então considere isso. \(4 y\left(25 x^{2}-20 x+4\right)\) É um trinômio quadrado perfeito? Verifique o padrão. 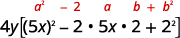
Fator. \(4 y(5 x-2)^{2}\) Lembre-se: mantenha o fator 4 y no produto final. Confira:
\[4y(5x−2)^2\nonumber\]\[4y[(5x)2−2·5x·2+22]\nonumber\]\[4y(25x2−20x+4)\nonumber\]100x2y−80xy+16y\ marca de verificação\]
Fator:\(8x^2y−24xy+18y\).
- Resposta
-
\(2y(2x−3)^2\)
Fator:\(27p^2q+90pq+75q\).
- Resposta
-
\(3q(3p+5)^2\)
Diferenças fatoriais dos quadrados
O outro produto especial que você viu no capítulo anterior foi o padrão Produto dos Conjugados. Você usou isso para multiplicar dois binômios que eram conjugados. Aqui está um exemplo:
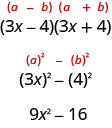
Uma diferença de fatores quadrados em relação a um produto de conjugados.
Se\(a\) e\(b\) forem números reais,
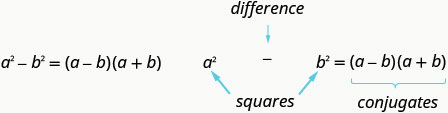
Lembre-se de que “diferença” se refere à subtração. Portanto, para usar esse padrão, você deve se certificar de ter um binômio no qual dois quadrados estão sendo subtraídos.
Fator:\(64y^2−1\).
- Resposta
-




Fator:\(121m^2−1\).
- Resposta
-
\((11m−1)(11m+1)\)
Fator:\(81y^2−1\).
- Resposta
-
\((9y−1)(9y+1)\)
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\)
É importante lembrar que as somas dos quadrados não são consideradas um produto de binômios. Não há fatores binomiais que se multipliquem para obter a soma dos quadrados. Depois de remover qualquer GCF, a expressão\(a^2+b^2\) é primordial!
O próximo exemplo mostra variáveis em ambos os termos.
Fator:\(144x^2−49y^2\).
- Resposta
-
\(\begin{array} {lll} &\quad &144x^2−49y^2 \\ \text{Is this a difference of squares? Yes.} &\quad &(12x)^2−(7y)^2 \\ \text{Factor as the product of conjugates.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad &(12x−7y)(12x+7y) \\ \text{Check by multiplying.} &\quad & \\ &\quad & \\ &\quad & \\ \hspace{14mm} (12x−7y)(12x+7y) &\quad & \\ \hspace{21mm} 144x^2−49y^2\checkmark &\quad & \end{array}\)
Fator:\(196m^2−25n^2\).
- Resposta
-
\((14m−5n)(14m+5n)\)
Fator:\(121p^2−9q^2\).
- Resposta
-
\((11p−3q)(11p+3q)\)
Como sempre, você deve procurar primeiro um fator comum sempre que tiver uma expressão para fatorar. Às vezes, um fator comum pode “disfarçar” a diferença de quadrados e você não reconhecerá os quadrados perfeitos até fatorar o GCF.
Além disso, para fatorar completamente o binômio no próximo exemplo, fatoraremos uma diferença de quadrados duas vezes!
Fator:\(48x^4y^2−243y^2\).
- Resposta
-
\(\begin{array} {ll} &48x^4y^2−243y^2 \\ \text{Is there a GCF? Yes, }3y^2\text{—factor it out!} &3y^2(16x^4−81) \\ \text{Is the binomial a difference of squares? Yes.} &3y^2\left((4x^2)^2−(9)^2\right) \\ \text{Factor as a product of conjugates.} &3y^2(4x^2−9)(4x^2+9) \\ \text{Notice the first binomial is also a difference of squares!} &3y^2((2x)^2−(3)^2)(4x^2+9) \\ \text{Factor it as the product of conjugates.} &3y^2(2x−3)(2x+3)(4x^2+9) \end{array}\)
O último fator, a soma dos quadrados, não pode ser fatorado.
\(\begin{array} {l} \text{Check by multiplying:} \\ \hspace{10mm} 3y^2(2x−3)(2x+3)(4x^2+9) \\ \\ \\ \hspace{15mm} 3y^2(4x^2−9)(4x^2+9) \\ \hspace{20mm} 3y^2(16x^4−81) \\ \hspace{19mm} 48x^4y^2−243y^2\checkmark\end{array}\)
Fator:\(2x^4y^2−32y^2\).
- Resposta
-
\(2y^2(x−2)(x+2)(x^2+4)\)
Fator:\(7a^4c^2−7b^4c^2\).
- Resposta
-
\(7c^2(a−b)(a+b)(a^2+b^2)\)
O próximo exemplo tem um polinômio com 4 termos. Até agora, quando isso ocorreu, agrupamos os termos em dois e fatoramos a partir daí. Aqui, notaremos que os três primeiros termos formam um trinômio quadrado perfeito.
Fator:\(x^2−6x+9−y^2\).
- Resposta
-
Observe que os três primeiros termos formam um trinômio quadrado perfeito.
\(x^{2}-6 x+9-y^{2}\) Considere agrupando os três primeiros termos. \(\underbrace{x^{2}-6 x+9} - y^{2}\) Use o padrão trinomial quadrado perfeito. \((x-3)^{2}-y^{2}\) Isso é uma diferença de quadrados? Sim. Sim, escreva-os como quadrados. 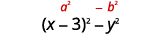
Fator como produto dos conjugados. 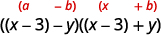
\((x-3-y)(x-3+y)\) Talvez você queira reescrever a solução como\((x−y−3)(x+y−3)\).
Fator:\(x^2−10x+25−y^2\).
- Resposta
-
\((x−5−y)(x−5+y)\)
Fator:\(x^2+6x+9−4y^2\).
- Resposta
-
\((x+3−2y)(x+3+2y)\)
Somas de fatores e diferenças de cubos
Há outro padrão especial para fatoração, um que não usamos quando multiplicamos polinômios. Esse é o padrão para a soma e a diferença dos cubos. Escreveremos essas fórmulas primeiro e depois as verificaremos por multiplicação.
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]
\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Verificaremos o primeiro padrão e deixaremos o segundo para você.
| \(\color{red}(a+b) \color{black} \left(a^{2}-a b+b^{2}\right)\) | |
| Distribuir. | \(\color{red}a \color{black}\left(a^{2}-a b+b^{2}\right)+ \color{red}b \color{black}\left(a^{2}-a b+b^{2}\right)\) |
| Multiplique. | \(a^{3}-a^{2} b+a b^{2}+a^{2} b-a b^{2}+b^{3}\) |
| Combine termos semelhantes. | \(a^{3}+b^{3}\) |
\[a^3+b^3=(a+b)(a^2−ab+b^2\nonumber\]\[a^3−b^3=(a−b)(a^2+ab+b^2)\nonumber\]
Os dois padrões parecem muito parecidos, não é? Mas observe os sinais nos fatores. O sinal do fator binomial corresponde ao sinal do binômio original. E o sinal do termo médio do fator trinomial é o oposto do sinal no binômio original. Se você reconhecer o padrão dos sinais, isso pode ajudá-lo a memorizar os padrões.

O fator trinomial no padrão de soma e diferença de cubos não pode ser fatorado.
É muito útil aprender a reconhecer os cubos dos números inteiros de 1 a 10, assim como aprendeu a reconhecer os quadrados. Listamos os cubos dos números inteiros de 1 a 10 na Tabela.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(n^3\) | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
Fator:\(x^3+64\).
- Resposta
-





Fator:\(x^3+27\).
- Resposta
-
\((x+3)(x^2−3x+9)\)
Fator:\(y^3+8\).
- Resposta
-
\((y+2)(y^2−2y+4)\)
- O binômio se ajusta ao padrão de soma ou diferença de cubos?
É uma soma ou diferença?
O primeiro e o último termo são cubos perfeitos? - Escreva-os como cubos.
- Use o padrão de soma ou diferença de cubos.
- Simplifique dentro dos parênteses.
- Verifique multiplicando os fatores.
Fator:\(27u^3−125v^3\).
- Resposta
-
\(27 u^{3}-125 v^{3}\) Esse binômio é uma diferença. O primeiro e o último
termo são cubos perfeitos.Escreva os termos como cubos. 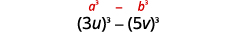
Use a diferença do padrão de cubos. 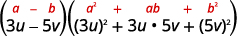
Simplifique. 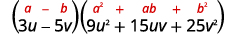
Verifique multiplicando. Vamos deixar o cheque para você.
Fator:\(8x^3−27y^3\).
- Resposta
-
\((2x−3y)(4x^2+6xy+9y^2)\)
Fator:\(1000m^3−125n^3\).
- Resposta
-
\((10m−5n)(100m^2+50mn+25n^2)\)
No próximo exemplo, primeiro consideramos o GCF. Então, podemos reconhecer a soma dos cubos.
Fator:\(6x^3y+48y^4\).
- Resposta
-
\(6 x^{3} y+48 y^{4}\) Considere o fator comum. \(6 y\left(x^{3}+8 y^{3}\right)\) Este binômio é uma soma. O primeiro e o último
termos são cubos perfeitos.Escreva os termos como cubos. 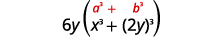
Use o padrão de soma de cubos. 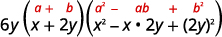
Simplifique. 
Confira:
Para verificar, talvez seja mais fácil multiplicar primeiro os fatores da soma dos cubos e depois multiplicar esse produto por 6y.6y. Vamos deixar a multiplicação para você.
Fator:\(500p^3+4q^3\).
- Resposta
-
\(4(5p+q)(25p^2−5pq+q^2)\)
Fator:\(432c^3+686d^3\).
- Resposta
-
\(2(6c+7d)(36c^2−42cd+49d^2)\)
O primeiro termo no próximo exemplo é um cubo binomial.
Fator:\((x+5)^3−64x^3\).
- Resposta
-
\((x+5)^{3}-64 x^{3}\) Esse binômio é uma diferença. O primeiro e o
último termo são cubos perfeitos.Escreva os termos como cubos. 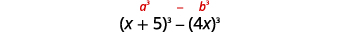
Use a diferença do padrão de cubos. 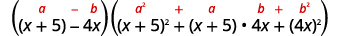
Simplifique. \((x+5-4 x)\left(x^{2}+10 x+25+4 x^{2}+20 x+16 x^{2}\right)\) \((-3 x+5)\left(21 x^{2}+30 x+25\right)\) Verifique multiplicando. Vamos deixar o cheque para você.
Fator:\((y+1)^3−27y^3\).
- Resposta
-
\((−2y+1)(13y^2+5y+1)\)
Fator:\((n+3)^3−125n^3\).
- Resposta
-
\((−4n+3)(31n^2+21n+9)\)
Acesse este recurso on-line para obter instruções e práticas adicionais com a fatoração de produtos especiais.
Conceitos-chave
- Padrão de trinômios quadrados perfeitos: Se a e b são números reais,
\[\begin{array} {l} a^2+2ab+b^2=(a+b)^2 \\ a^2−2ab+b^2=(a−b)^2\end{array} \nonumber\]
- Como fatorar trinômios quadrados perfeitos.
\(\begin{array} {lllll} \textbf{Step 1.} &\text{Does the trinomial fit the pattern?} &\quad &\hspace{7mm} a^2+2ab+b^2 &\hspace{7mm} a^2−2ab+b^2 \\ &\text{Are the first and last terms perfect squares?} &\quad & &\\ &\text{Write them as squares.} &\quad &\hspace{5mm}(a)^2\hspace{16mm} (b)^2 &\hspace{6mm}(a)^2\hspace{16mm} (b)^2 \\ &\text{Check the middle term. Is it }2ab? &\quad &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} &\hspace{12mm} {\,}^{\searrow}{\,}_{2·a·b}{\,}^{\swarrow} \\ \textbf{Step 2.} &\text{Write the square of the binomial.} &\quad &\hspace{13mm} (a+b)^2 &\hspace{13mm} (a−b)^2 \\ \textbf{Step 3.} &\text{Check by multiplying.} & & & \end{array}\) - Padrão de diferença de quadrados: Se a, ba, b são números reais,
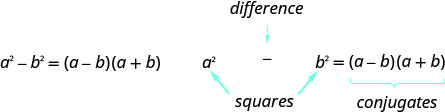
- Como fatorar as diferenças dos quadrados.
\(\begin{array} {llll} \textbf{Step 1.} &\text{Does the binomial fit the pattern?} &\qquad &\hspace{5mm} a^2−b^2 \\ &\text{Is this a difference?} &\qquad &\hspace{2mm} \text{____−____} \\ &\text{Are the first and last terms perfect squares?} & & \\ \textbf{Step 2.} &\text{Write them as squares.} &\qquad &\hspace{3mm} (a)^2−(b)^2 \\ \textbf{Step 3.} &\text{Write the product of conjugates.} &\qquad &(a−b)(a+b) \\ \textbf{Step 4.} &\text{Check by multiplying.} & & \end{array}\) - Padrão de soma e diferença de cubos
\(\begin{array} {l} a^3+b3=(a+b)(a^2−ab+b^2) \\ a^3−b^3=(a−b)(a^2+ab+b^2) \end{array} \) - Como fatorar a soma ou a diferença dos cubos.
- O binômio se ajusta ao padrão de soma ou diferença de cubos?
É uma soma ou diferença?
O primeiro e o último termo são cubos perfeitos? - Escreva-os como cubos.
- Use o padrão de soma ou diferença de cubos.
- Simplifique dentro dos parênteses
- Verifique multiplicando os fatores.
- O binômio se ajusta ao padrão de soma ou diferença de cubos?


