4.2: Resolva sistemas de equações lineares com duas variáveis
- Page ID
- 183232
Ao final desta seção, você poderá:
- Determine se um par ordenado é uma solução de um sistema de equações
- Resolva um sistema de equações lineares representando graficamente
- Resolva um sistema de equações por substituição
- Resolva um sistema de equações por eliminação
- Escolha o método mais conveniente para resolver um sistema de equações lineares
Antes de começar, faça este teste de prontidão.
- Para a equação\(y=\frac{2}{3}x−4\),
ⓐ É\((6,0)\) uma solução? ⓑ É\((−3,−2)\) uma solução?
Se você perdeu esse problema, revise [link]. - Encontre a inclinação e a interceptação y da linha\(3x−y=12\).
Se você perdeu esse problema, revise [link]. - Encontre as interceptações x e y da linha\(2x−3y=12\).
Se você perdeu esse problema, revise [link].
Determine se um par ordenado é uma solução de um sistema de equações
Em Solução de equações lineares, aprendemos como resolver equações lineares com uma variável. Agora, trabalharemos com duas ou mais equações lineares agrupadas, o que é conhecido como sistema de equações lineares.
Quando duas ou mais equações lineares são agrupadas, elas formam um sistema de equações lineares.
Nesta seção, focaremos nosso trabalho em sistemas de duas equações lineares em duas incógnitas. Resolveremos sistemas maiores de equações mais adiante neste capítulo.
Um exemplo de um sistema de duas equações lineares é mostrado abaixo. Usamos uma chave para mostrar que as duas equações estão agrupadas para formar um sistema de equações.
\[ \left\{ \begin{aligned} 2x+y & = 7 \\ x−2y & = 6 \end{aligned} \right. \nonumber \]
Uma equação linear em duas variáveis, como\(2x+y=7\), tem um número infinito de soluções. Seu gráfico é uma linha. Lembre-se de que cada ponto na linha é uma solução para a equação e cada solução para a equação é um ponto na linha.
Para resolver um sistema de duas equações lineares, queremos encontrar os valores das variáveis que são soluções para ambas as equações. Em outras palavras, estamos procurando os pares ordenados\((x,y)\) que tornam as duas equações verdadeiras. Essas são chamadas de soluções de um sistema de equações.
As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras. A solução de um sistema de duas equações lineares é representada por um par ordenado\((x,y)\).
Para determinar se um par ordenado é uma solução para um sistema de duas equações, substituímos os valores das variáveis em cada equação. Se o par ordenado tornar as duas equações verdadeiras, é uma solução para o sistema.
Determine se o par pedido é uma solução para o sistema\(\left \{ \begin{array} {l} x−y = −1 \\ 2x−y = −5 \end{array} \right. \).
ⓐ\((−2,−1)\) ⓑ\((−4,−3)\)
- Responda
-
ⓐ
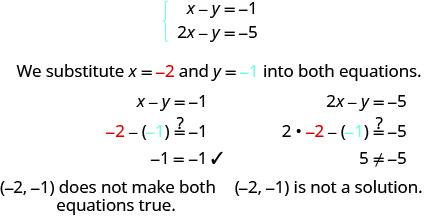
ⓑ
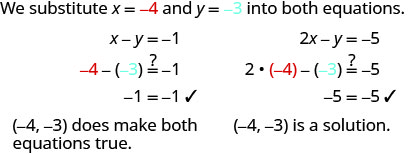
Determine se o par pedido é uma solução para o sistema\(\left \{ \begin{array} 3x+y = 0 \\ x+2y = −5 \end{array} \right. \).
ⓐ\((1,−3)\) ⓑ\((0,0)\)
- Responda
-
ⓐ sim ⓑ não
Determine se o par pedido é uma solução para o sistema\(\left \{ \begin{array} x−3y = −8 \\ −3x−y = 4 \end{array} \right. \).
ⓐ\((2,−2)\) ⓑ\((−2,2)\)
- Responda
-
ⓐ não ⓑ sim
Resolva um sistema de equações lineares por meio de gráficos
Nesta seção, usaremos três métodos para resolver um sistema de equações lineares. O primeiro método que usaremos é a representação gráfica.
O gráfico de uma equação linear é uma linha. Cada ponto na linha é uma solução para a equação. Para um sistema de duas equações, representaremos graficamente duas linhas. Então, podemos ver todos os pontos que são soluções para cada equação. E, ao descobrir o que as linhas têm em comum, encontraremos a solução para o sistema.
A maioria das equações lineares em uma variável tem uma solução, mas vimos que algumas equações, chamadas contradições, não têm soluções e para outras equações, chamadas identidades, todos os números são soluções.
Da mesma forma, quando resolvemos um sistema de duas equações lineares representadas por um gráfico de duas linhas no mesmo plano, há três casos possíveis, conforme mostrado.
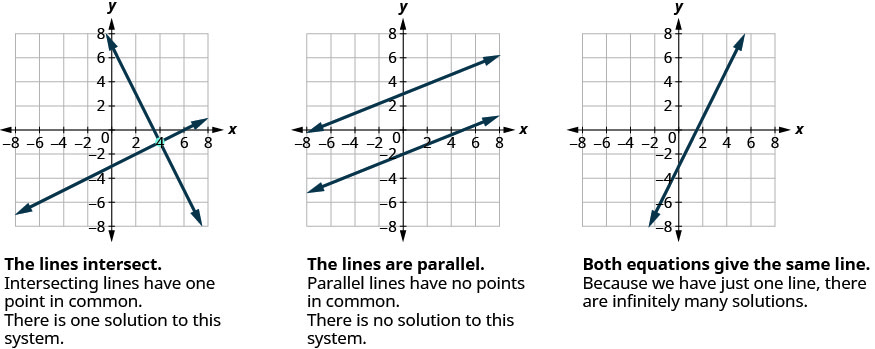
Cada vez que demonstrarmos um novo método, nós o usaremos no mesmo sistema de equações lineares. No final da seção, você decidirá qual método era a maneira mais conveniente de resolver esse sistema.
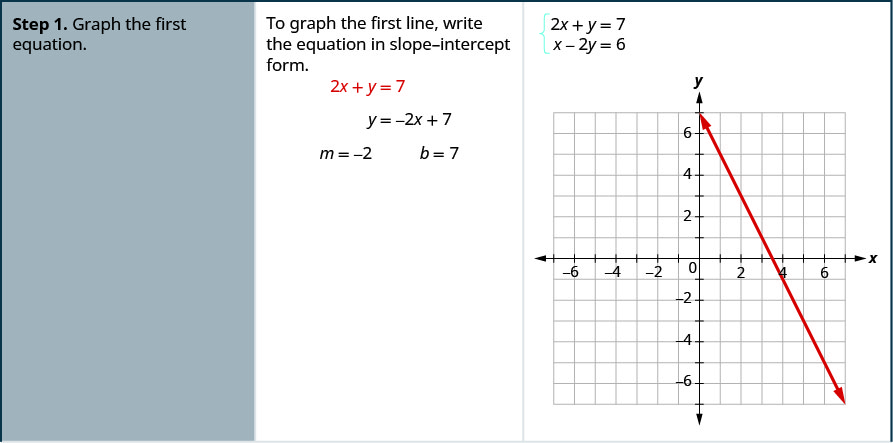
Resolva o sistema representando graficamente\( \left\{ \begin{array} {l} 2x+y = 7 \\ x−2y = 6 \end{array} \right. \).
- Responda
-


Resolva o sistema representando graficamente:\( \left\{ \begin{array} {l} x−3y = −3 \\ x+y = 5 \end{array} \right. \).
- Responda
-
\((3,2)\)
Resolva o sistema representando graficamente:\( \left\{ \begin{array} {l} −x+y = 1 \\ 3x+2y = 12 \end{array} \right.\)
- Responda
-
\((2,3)\)
As etapas a serem usadas para resolver um sistema de equações lineares por meio de gráficos são mostradas aqui.
- Faça um gráfico da primeira equação.
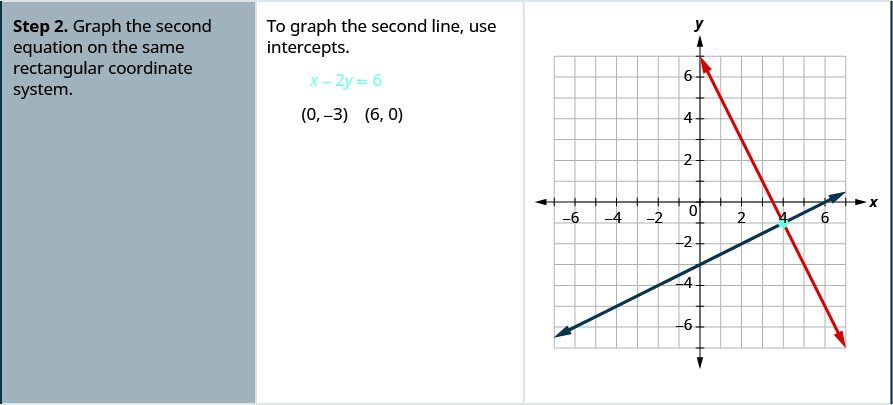
- Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
- Determine se as linhas se cruzam, são paralelas ou são a mesma linha.
- Identifique a solução para o sistema.
- Se as linhas se cruzarem, identifique o ponto de interseção. Essa é a solução para o sistema.
- Se as linhas estiverem paralelas, o sistema não tem solução.
- Se as linhas forem iguais, o sistema tem um número infinito de soluções.
- Verifique a solução nas duas equações.
No próximo exemplo, primeiro reescreveremos as equações na forma de inclinação e interceptação, pois isso facilitará a representação gráfica rápida das linhas.
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} 3x+y = −1 \\ 2x+y = 0 \end{array}\right.\)
- Responda
-
Resolveremos essas duas equações para que\(y\) possamos facilmente representá-las graficamente usando suas inclinações e\(y\) interceptações.
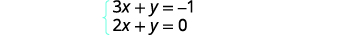
Resolva a primeira equação para y. 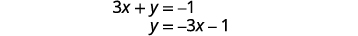
Encontre a inclinação e a interceptação y. 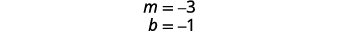
Resolva a segunda equação para y. 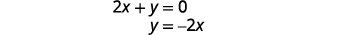
Encontre a inclinação e a interceptação y. 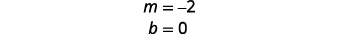
Faça um gráfico das linhas. 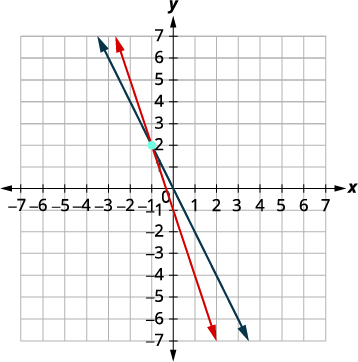
Determine o ponto de interseção. As linhas se cruzam em\((−1,2)\). Verifique a solução nas duas equações.
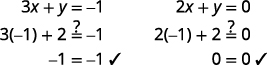
A solução é\((−1,2)\).
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} −x+y = 1 \\2x+y = 10 \end{array}\right. \).
- Responda
-
\((3,4)\)
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} 2x+y = 6 \\x+y = 1 \end{array}\right. \).
- Responda
-
\((5,−4)\)
Em todos os sistemas de equações lineares até agora, as linhas se cruzaram e a solução foi um ponto. Nos próximos dois exemplos, veremos um sistema de equações que não tem solução e um sistema de equações que tem um número infinito de soluções.
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-3 \\ x-2y = 4 \end{array}\right. \).
- Responda
-
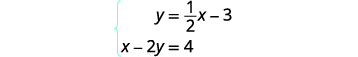
Para representar graficamente a primeira equação, usaremos sua
inclinação e intercepto y.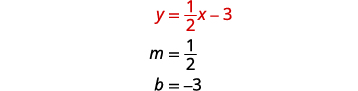
Para representar graficamente a segunda equação, usaremos
os interceptos.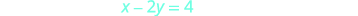
Faça um gráfico das linhas. 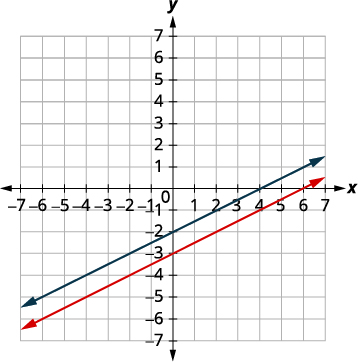
Determine os pontos de interseção. As linhas são paralelas.
Como nenhum ponto está nas duas linhas, não há um par
ordenado que torne ambas as equações
verdadeiras. Não há solução para esse sistema.
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = -\tfrac{1}{4}x+2 \\ x+4y = 4 \end{array}\right. \).
- Responda
-
sem solução
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = 3x-1 \\ 6x-2y = 6 \end{array}\right. \).
- Responda
-
sem solução
Às vezes, as equações em um sistema representam a mesma linha. Como cada ponto na reta torna as duas equações verdadeiras, há infinitos pares ordenados que tornam ambas as equações verdadeiras. Existem infinitas soluções para o sistema.
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = 2x-3 \\ -6x+3y = 9 \end{array}\right. \).
- Responda
-
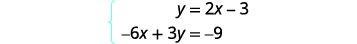
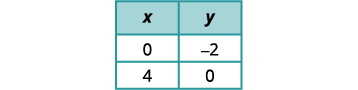
Encontre a inclinação e a interceptação y da primeira equação. 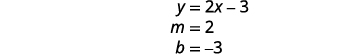
Encontre os interceptos da segunda equação. 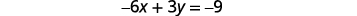
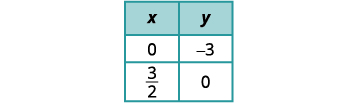
Faça um gráfico das linhas. 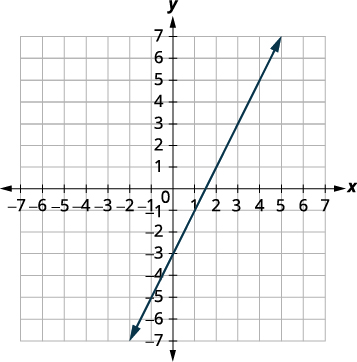
As linhas são as mesmas!
Como cada ponto na reta torna as duas
equações verdadeiras, há infinitos pares
ordenados que tornam ambas as equações verdadeiras.
Existem infinitas soluções para esse sistema.Se você escrever a segunda equação na forma de interceptação de inclinação, poderá reconhecer que as equações têm a mesma inclinação e o mesmo intercepto y.
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = -3x-6 \\ 6x+2y = -12 \end{array}\right. \).
- Responda
-
infinitas soluções
Resolva o sistema representando graficamente:\(\left\{ \begin{array} {l} y = \tfrac{1}{2}x-4 \\ 2x-4y = 16 \end{array}\right. \).
- Responda
-
infinitas soluções
Quando representamos graficamente a segunda linha no último exemplo, nós a desenhamos logo acima da primeira linha. Dizemos que as duas linhas são coincidentes. As linhas coincidentes têm a mesma inclinação e o mesmo intercepto y.
As linhas coincidentes têm a mesma inclinação e o mesmo intercepto y.
Cada um dos sistemas de equações em Exemplo e Exemplo tinha duas linhas que se cruzam. Cada sistema tinha uma solução.
No exemplo, as equações deram linhas coincidentes e, portanto, o sistema tinha infinitas soluções.
Os sistemas nesses três exemplos tinham pelo menos uma solução. Um sistema de equações que tem pelo menos uma solução é chamado de sistema consistente.
Um sistema com linhas paralelas, como o Example, não tem solução. Chamamos um sistema de equações como esse de inconsistente. Não tem solução.
Um sistema consistente de equações é um sistema de equações com pelo menos uma solução.
Um sistema de equações inconsistente é um sistema de equações sem solução.
Também categorizamos as equações em um sistema de equações chamando-as de independentes ou dependentes. Se duas equações forem independentes, cada uma delas terá seu próprio conjunto de soluções. As linhas que se cruzam e as linhas paralelas são independentes.
Se duas equações são dependentes, todas as soluções de uma equação também são soluções da outra equação. Quando representamos graficamente duas equações dependentes, obtemos linhas coincidentes.
Vamos resumir isso examinando os gráficos dos três tipos de sistemas. Veja abaixo e a tabela.
| Linhas | Cruzando | Paralela | Coincidente |
|---|---|---|---|
| Número de soluções | 1 ponto | Sem solução | Infinitamente muitos |
| Consistente/inconsistente | Consistente | Inconsistente | Consistente |
| Dependente/independente | Independente | Independente | Dependente |
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
ⓐ\( \left\{ \begin{array} {l} y = 3x−1 \\ 6x−2y = 12 \end{array}\right. \) ⓑ\( \left\{ \begin{array} {l} 2x+y=−3 \\ x−5y=5 \end{array} \right. \)
- Responda
-
ⓐ Vamos comparar as inclinações e interceptações das duas linhas.
\(\begin{array} {lll} {} &{} &{ \left\{ \begin{array} {l} {y=3x-1} \\ {6x−2y=12} \end{array} \right. } \\ {} &{} &{y = 3x-1} \\ {\text{The first equation is already in slope-intercept form.}} &{} &{} \\ {\text{Write the second equation in slope-intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{6x-2y=12} \\ {} &{} &{-2y=-6x+12} \\ {} &{} &{\frac{-2y}{-2}=\frac{-6x+12}{-2}} \\ {} &{} &{y=3x-6} \\ {} &{y=3x-1} &{y=3x-6} \\ {} &{m=3} &{m=3} \\ {} &{b=-1} &{b=-6} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{\text{Since the slopes are the same andy-intercepts are}} &{} \\ {} &{\text{different, the lines are parallel.}} &{} \\ \end{array}\)
ⓑ Vamos comparar a inclinação e as interceptações das duas linhas.
\(\begin{array} {lll} {} &{} &{} \\ {} &{ \left\{ \begin{array} {l} 2x+y=-3 \\ x-5y=5 \\ \end{array} \right. } &{} \\ {\text{Write both equations in slope–intercept form.}} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{2x+y=-3} &{x-5y=5} \\ {} &{y=-2x-3} &{-5y=-x+5} \\ {} &{} &{\frac{-5y}{-5}=\frac{-x+5}{-5}} \\ {} &{} &{y=\frac{1}{5}-1} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {} &{} &{} \\ {\text{Find the slope and intercept of each line.}} &{} &{} \\ {} &{} &{} \\ {} &{y=-2x-3} &{y=\frac{1}{5}-1} \\ {} &{m=-2} &{m=\frac{1}{5}} \\ {} &{b=-3} &{b=-1} \\ {} &{} &{} \\ {} &{\text{Since the slopes are different, the lines intersect.}} &{} \\ \end{array}\)
Um sistema de equações cujos gráficos são cruzados tem 1 solução e é consistente e independente.
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
ⓐ\(\left\{ \begin{array} {l} y=−2x−4 \\ 4x+2y=9 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} 3x+2y=2 \\ 2x+y=1 \end{array} \right. \)
- Responda
-
ⓐ nenhuma solução, inconsistente, independente ⓑ uma solução, consistente, independente
Sem representar graficamente, determine o número de soluções e depois classifique o sistema de equações.
ⓐ\(\left\{ \begin{array} {l} y=\frac{1}{3}x−5 \\ x−3y=6 \end{array} \right. \) ⓑ\(\left\{ \begin{array} {l} x+4y=12 \\ −x+y=3 \end{array} \right. \)
- Responda
-
ⓐ nenhuma solução, inconsistente, independente ⓑ uma solução, consistente, independente
Resolver sistemas de equações lineares por meio de gráficos é uma boa maneira de visualizar os tipos de soluções que podem resultar. No entanto, há muitos casos em que resolver um sistema por meio de gráficos é inconveniente ou impreciso. Se os gráficos se estenderem além da pequena grade com x e y entre\(−10\) e 10, representar graficamente as linhas pode ser complicado. E se as soluções para o sistema não forem números inteiros, pode ser difícil ler seus valores com precisão em um gráfico.
Resolva um sistema de equações por substituição
Agora resolveremos sistemas de equações lineares pelo método de substituição.
Usaremos o mesmo sistema que usamos primeiro para representar graficamente.
\[ \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \nonumber \]
Primeiro resolveremos uma das equações para x ou y. Podemos escolher qualquer uma das equações e resolver qualquer uma das variáveis, mas tentaremos fazer uma escolha que facilite o trabalho.
Em seguida, substituímos essa expressão na outra equação. O resultado é uma equação com apenas uma variável — e sabemos como resolvê-las!
Depois de encontrarmos o valor de uma variável, substituiremos esse valor em uma das equações originais e resolveremos a outra variável. Finalmente, verificamos nossa solução e garantimos que ela torne as duas equações verdadeiras.
Resolva o sistema por substituição:\( \left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- Responda
-






Resolva o sistema por substituição:\( \left\{ \begin{array} {l} −2x+y=−11 \\ x+3y=9 \end{array} \right. \)
- Responda
-
\((6,1)\)
Resolva o sistema por substituição:\( \left\{ \begin{array} {l} 2x+y=−1 \\ 4x+3y=3 \end{array} \right. \)
- Responda
-
\((−3,5)\)
- Resolva uma das equações para qualquer variável.
- Substitua a expressão da Etapa 1 pela outra equação.
- Resolva a equação resultante.
- Substitua a solução na Etapa 3 em qualquer uma das equações originais para encontrar a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
Tenha muito cuidado com os sinais no próximo exemplo.
Resolva o sistema por substituição:\( \left\{ \begin{array} {l} 4x+2y=4 \\ 6x−y=8 \end{array} \right. \)
- Responda
-
Precisamos resolver uma equação para uma variável. Resolveremos a primeira equação para y.
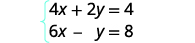
Resolva a primeira equação para y.
\(−2x+2\)Substitua y na segunda equação.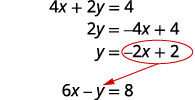
Substitua o y por\(−2x+2\). 
Resolva a equação para x. 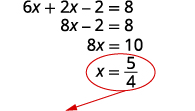
\(4x+2y=4\)Substitua\(x=54\) em para encontrar y. 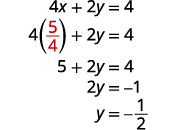
O par pedido é\((54,−12)\). Verifique o par ordenado nas duas equações.
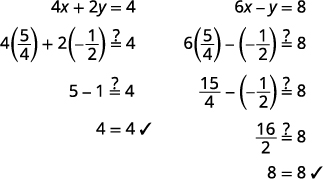
A solução é\((54,−12)\).
Resolva o sistema por substituição:\( \left\{ \begin{array} {l} x−4y=−4 \\ −3x+4y=0 \end{array} \right. \)
- Responda
-
\((2,32)\)
Resolva o sistema por substituição:\( \left\{ \begin{array} {l} 4x−y=0 \\ 2x−3y=5 \end{array} \right. \)
- Responda
-
\((−12,−2)\)
Resolva um sistema de equações por eliminação
Resolvemos sistemas de equações lineares por representação gráfica e por substituição. A representação gráfica funciona bem quando os coeficientes variáveis são pequenos e a solução tem valores inteiros. A substituição funciona bem quando podemos resolver facilmente uma equação para uma das variáveis e não ter muitas frações na expressão resultante.
O terceiro método de resolução de sistemas de equações lineares é chamado de Método de Eliminação. Quando resolvemos um sistema por substituição, começamos com duas equações e duas variáveis e o reduzimos a uma equação com uma variável. Isso também é o que faremos com o método de eliminação, mas teremos uma maneira diferente de chegar lá.
O Método de Eliminação é baseado na Propriedade de Adição da Igualdade. A Propriedade de Adição da Igualdade diz que quando você adiciona a mesma quantidade aos dois lados de uma equação, você ainda tem igualdade. Estenderemos a Propriedade de Adição de Igualdade para dizer que quando você adiciona quantidades iguais aos dois lados de uma equação, os resultados são iguais.
Para qualquer expressão a, b, c e d.
\[\begin{array} {ll} {\text{if}} &{a=b} \\ {\text{and}} &{c=d} \\ {\text{then}} &{a+c=b+d.} \\ \nonumber \end{array}\]
Para resolver um sistema de equações por eliminação, começamos com as duas equações na forma padrão. Em seguida, decidimos qual variável será mais fácil de eliminar. Como podemos decidir? Queremos que os coeficientes de uma variável sejam opostos, para que possamos somar as equações e eliminar essa variável.
Observe como isso funciona quando adicionamos essas duas equações:
\[\left\{ \begin{array} {l} 3x+y=5 \\ \underline{2x−y=0} \end{array} \right. \nonumber\]
\[5x=5 \nonumber\]
Os y's somam a zero e temos uma equação com uma variável.
Vamos tentar outro:
\[ \left\{ \begin{array} x+4y=2 \\ 2x+5y=−2 \end{array} \right. \nonumber\]
Desta vez, não vemos uma variável que possa ser eliminada imediatamente se somarmos as equações.
Mas se multiplicarmos a primeira equação por\(−2\), criaremos os coeficientes de x opostos. Devemos multiplicar cada termo em ambos os lados da equação por\(−2\).
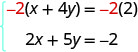
Em seguida, reescreva o sistema de equações.
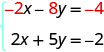
Agora vemos que os coeficientes dos termos x são opostos, então x será eliminado quando adicionarmos essas duas equações.
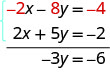
Depois de obtermos uma equação com apenas uma variável, nós a resolvemos. Em seguida, substituímos esse valor em uma das equações originais para resolver a variável restante. E, como sempre, verificamos nossa resposta para garantir que seja uma solução para ambas as equações originais.
Agora veremos como usar a eliminação para resolver o mesmo sistema de equações que resolvemos por meio de gráficos e por substituição.
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 2x+y=7 \\ x−2y=6 \end{array} \right. \)
- Responda
-






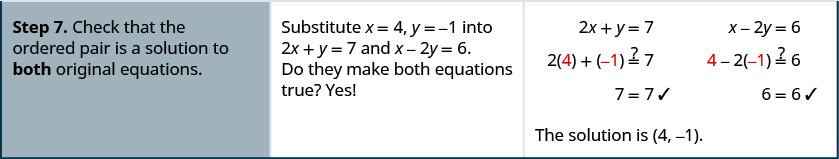
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 3x+y=5 \\ 2x−3y=7 \end{array} \right.\)
- Responda
-
\((2,−1)\)
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 4x+y=−5 \\ −2x−2y=−2 \end{array} \right.\)
- Responda
-
\((−2,3)\)
As etapas estão listadas aqui para facilitar a referência.
- Escreva as duas equações na forma padrão. Se algum coeficiente for fracionário, limpe-o.
- Faça os coeficientes de uma variável oposta.
- Decida qual variável você eliminará.
- Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos.
- Adicione as equações resultantes da Etapa 2 para eliminar uma variável.
- Resolva a variável restante.
- Substitua a solução da Etapa 4 em uma das equações originais. Em seguida, resolva a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
Agora vamos fazer um exemplo em que precisamos multiplicar as duas equações por constantes para fazer com que os coeficientes de uma variável sejam opostos.
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 4x−3y=9 \\ 7x+2y=−6 \end{array} \right. \)
- Responda
-
Neste exemplo, não podemos multiplicar apenas uma equação por qualquer constante para obter coeficientes opostos. Portanto, multiplicaremos estrategicamente as duas equações por diferentes constantes para obter os opostos.
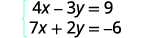
Ambas as equações estão na forma padrão.
Para obter coeficientes opostos de y,
multiplicaremos a primeira equação por 2 e a
segunda equação por 3.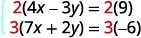
Simplifique. 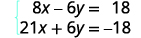
Adicione as duas equações para eliminar y. 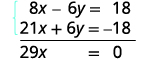
Resolva para x. 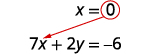
Substitua x=0x=0 em uma das equações originais. 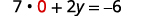
Resolva para y. 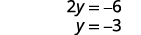
Escreva a solução como um par ordenado. O par pedido é\((0,−3)\).
Verifique se o par ordenado é uma solução para
ambas as equações originais.
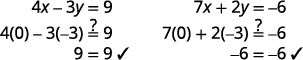
A solução é\((0,−3)\).
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 3x−4y=−9 \\ 5x+3y=14\end{array} \right. \)
- Responda
-
\((1,3)\)
Resolva cada sistema por eliminação:\(\left\{ \begin{array} {l} 7x+8y=4 \\ 3x−5y=27 \end{array} \right.\)
- Responda
-
\((4,−3)\)
Quando o sistema de equações contém frações, primeiro eliminaremos as frações multiplicando cada equação pelo LCD de todas as frações na equação.
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} x+\tfrac{1}{2}y=6 \\ \tfrac{3}{2}x+\tfrac{2}{3}y=\tfrac{17}{2} \end{array} \right.\)
- Responda
-
Neste exemplo, ambas as equações têm frações. Nosso primeiro passo será multiplicar cada equação pelo LCD de todas as frações na equação para limpar as frações.
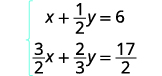
Para limpar as frações, multiplique cada
equação pelo LCD.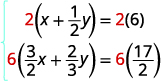
Simplifique. 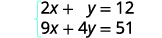
Agora estamos prontos para eliminar uma
das variáveis. Observe que ambas as equações estão na forma
padrão.Podemos eliminar y multiplicando a equação superior por\(−4\). 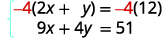
Simplifique e acrescente.
\(x=3\)Substitua em uma das equações originais.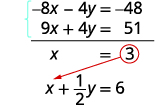
Resolva para y. 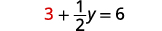
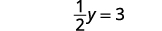
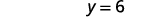
Escreva a solução como um par ordenado. O par pedido é\((3,6)\). Verifique se o par ordenado é uma solução para
ambas as equações originais.

A solução é\((3,6)\).
Resolva cada sistema por eliminação:\(\left\{ \begin{array} {l} \tfrac{1}{3}x−\tfrac{1}{2}y=1 \\ \tfrac{3}{4}x−y=\tfrac{5}{2} \end{array} \right.\)
- Responda
-
\((6,2)\)
Resolva cada sistema por eliminação:\(\left\{ \begin{array} {l} x+\tfrac{3}{5}y=−\tfrac{1}{5} \\ −\tfrac{1}{2}x−\tfrac{2}{3}y=\tfrac{5}{6} \end{array} \right.\)
- Responda
-
\((1,−2)\)
Quando resolvemos o sistema por meio de gráficos, vimos que nem todos os sistemas de equações lineares têm um único par ordenado como solução. Quando as duas equações eram realmente a mesma reta, havia infinitas soluções. Chamamos isso de sistema consistente. Quando as duas equações descreveram retas paralelas, não havia solução. Chamamos isso de sistema inconsistente.
O mesmo acontece com a substituição ou eliminação. Se a equação no final da substituição ou eliminação for uma afirmação verdadeira, temos um sistema consistente, mas dependente, e o sistema de equações tem infinitas soluções. Se a equação no final da substituição ou eliminação for uma afirmação falsa, temos um sistema inconsistente e o sistema de equações não tem solução.
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\tfrac{3}{4}x \end{array} \right. \)
- Responda
-
\(\begin{array} {ll} {} &{ \left\{ \begin{array} {l} 3x+4y=12 \\ y=3−\frac{3}{4}x \end{array} \right.} \\ {} &{} \\ {\text{Write the second equation in standard form.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ \frac{3}{4}x+y=3 \end{array} \right. } \\ {} &{} \\ {\text{Clear the fractions by multiplying the } \\ \text{second equation by 4.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 4(\frac{3}{4}x+y)=4(3) \end{array} \right. } \\ {} &{} \\ {\text{Simplify.}} &{\left\{ \begin{array} {l} 3x+4y=12 \\ 3x+4y=12 \end{array} \right. } \\ {} &{} \\ {\text{To eliminate a variable, we multiply the} \\ \text{second equation by−1. Simplify and add.}} &{\begin{array} {l} {\left\{ \begin{array} {l} 3x+4y=12 \\ \underline{-3x-4y=-12 } \end{array} \right.} \\ {\hspace{16mm} 0=0} \end{array}} \\ \end{array} \)
Essa é uma afirmação verdadeira. As equações são consistentes, mas dependentes. Seus gráficos seriam a mesma linha. O sistema tem infinitas soluções.
Depois de limparmos as frações na segunda equação, você notou que as duas equações eram iguais? Isso significa que temos linhas coincidentes.
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} 5x−3y=15 \\ 5y=−5+\tfrac{5}{3}x \end{array} \right. \)
- Responda
-
infinitas soluções
Resolva o sistema por eliminação:\(\left\{ \begin{array} {l} x+2y=6 \\ y=−\tfrac{1}{2}x+3\end{array} \right. \)
- Responda
-
infinitas soluções
Escolha o método mais conveniente para resolver um sistema de equações lineares
Ao resolver um sistema de equações lineares em um aplicativo, você não será informado sobre qual método usar. Você precisará tomar essa decisão sozinho. Então, você deve escolher o método mais fácil de fazer e minimizar suas chances de cometer erros.
\[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{Use when you need a}} &{\text{Use when one equation is}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{already solved or can be}} &{\text{rein standard form.}} \\ {\text{}} &{\text{easily solved for one}} &{\text{}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.
ⓐ\(\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\)
- Responda
-
ⓐ
\[\left\{ \begin{array} {l} 3x+8y=40 \\ 7x−4y=−32 \end{array} \right.\nonumber\]
Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente.
ⓑ
\[\left\{ \begin{array} {l} 5x+6y=12 \\ y=\tfrac{2}{3}x−1 \end{array} \right.\nonumber \]
Como uma equação já foi resolvida para y, usar a substituição será mais conveniente.
Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.
ⓐ\(\left\{ \begin{array} {l} 4x−5y=−32 \\ 3x+2y=−1 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} x=2y−1 \\ 3x−5y=−7 \end{array} \right.\)
- Responda
-
ⓐ Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente. ⓑ Como uma equação já foi resolvida para x, usar a substituição será mais conveniente.
Para cada sistema de equações lineares, decida se seria mais conveniente resolvê-lo por substituição ou eliminação. Explique sua resposta.
ⓐ\(\left\{ \begin{array} {l} y=2x−1 \\ 3x−4y=−6 \end{array} \right.\) ⓑ\(\left\{ \begin{array} {l} 6x−2y=12 \\ 3x+7y=−13 \end{array} \right.\)
- Responda
-
ⓐ Como uma equação já foi resolvida para y, usar a substituição será mais conveniente. ⓑ Como as duas equações estão na forma padrão, usar a eliminação será mais conveniente.
Conceitos-chave
- Como resolver um sistema de equações lineares por meio de gráficos.
- Faça um gráfico da primeira equação.
- Faça um gráfico da segunda equação no mesmo sistema de coordenadas retangulares.
- Determine se as linhas se cruzam, são paralelas ou são a mesma linha.
- Identifique a solução para o sistema.
Se as linhas se cruzarem, identifique o ponto de interseção. Essa é a solução para o sistema.
Se as linhas estiverem paralelas, o sistema não tem solução.
Se as linhas forem iguais, o sistema tem um número infinito de soluções. - Verifique a solução nas duas equações.
- Como resolver um sistema de equações por substituição.
- Resolva uma das equações para qualquer variável.
- Substitua a expressão da Etapa 1 pela outra equação.
- Resolva a equação resultante.
- Substitua a solução na Etapa 3 em qualquer uma das equações originais para encontrar a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais.
- Como resolver um sistema de equações por eliminação.
- Escreva as duas equações na forma padrão. Se algum coeficiente for fracionário, limpe-o.
- Faça os coeficientes de uma variável oposta.
Decida qual variável você eliminará.
Multiplique uma ou ambas as equações para que os coeficientes dessa variável sejam opostos. - Adicione as equações resultantes da Etapa 2 para eliminar uma variável.
- Resolva a variável restante.
- Substitua a solução da Etapa 4 em uma das equações originais. Em seguida, resolva a outra variável.
- Escreva a solução como um par ordenado.
- Verifique se o par ordenado é uma solução para ambas as equações originais. \[ \textbf{Choose the Most Convenient Method to Solve a System of Linear Equations} \\ \begin{array} {lll} {\underline{\textbf{Graphing}}} &{\underline{\textbf{Substitution}}} &{\underline{\textbf{Elimination}}} \\ {\text{}} &{\text{Use when one equation is}} &{\text{}} \\ {\text{Use when you need a}} &{\text{already solved or can be}} &{\text{Use when the equations a}} \\ {\text{picture of the situation.}} &{\text{easily solved for one}} &{\text{rein standard form.}} \\ {\text{}} &{\text{variable.}} &{\text{}} \\ \end{array} \nonumber \]
Glossário
- linhas coincidentes
- As linhas coincidentes têm a mesma inclinação e o mesmo intercepto y.
- sistemas consistentes e inconsistentes
- Sistema consistente de equações é um sistema de equações com pelo menos uma solução; sistema de equações inconsistente é um sistema de equações sem solução.
- soluções de um sistema de equações
- As soluções de um sistema de equações são os valores das variáveis que tornam todas as equações verdadeiras; a solução é representada por um par ordenado (x, y). (x, y).
- sistema de equações lineares
- Quando duas ou mais equações lineares são agrupadas, elas formam um sistema de equações lineares.