Capítulo 3 Exercícios de revisão

Last updated
Save as PDF

Page ID: 183047

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercícios de revisão de

Representar graficamente equações lineares em duas variáveis

Traçar pontos em um sistema de coordenadas retangulares

Nos exercícios a seguir, plote cada ponto em um sistema de coordenadas retangular.

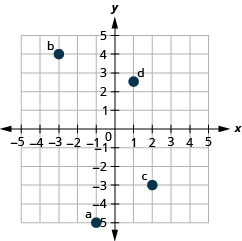
1. ⓐ$(−1,−5)$
ⓑ$(−3,4)$
ⓒ$(2,−3)$
ⓓ$(1,\frac{5}{2})$

Resposta: $Esta figura mostra os pontos traçados no plano da coordenada x y. Os eixos x e y vão de menos 5 a 5. O ponto rotulado como a está 1 unidade à esquerda da origem e 5 unidades abaixo da origem e está localizado no quadrante III. O ponto rotulado b está 3 unidades à esquerda da origem e 4 unidades acima da origem e está localizado no quadrante II. O ponto marcado com c está 2 unidades à direita da origem e 3 unidades abaixo da origem e está localizado no quadrante IV. O ponto marcado com d está 1 unidade à direita da origem e 2,5 unidades acima da origem e está localizado no quadrante I.$

2. ⓐ$(−2,0)$
ⓑ$(0,−4)$
ⓒ$(0,5)$
ⓓ$(3,0)$

Nos exercícios a seguir, determine quais pares ordenados são soluções para as equações dadas.

3. $5x+y=10$;

ⓐ$(5,1)$
ⓑ$(2,0)$
ⓒ$(4,−10)$

Resposta: ⓑ, ⓒ

4. $y=6x−2$;

ⓐ$(1,4)$
ⓑ$(13,0)$
ⓒ$(6,−2)$

Representar graficamente uma equação linear traçando pontos

Nos exercícios a seguir, desenhe graficamente pontos.

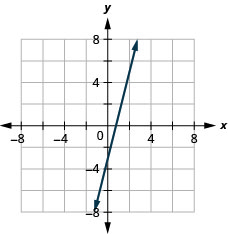
5. $y=4x−3$

Resposta: $Esta figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 1, menos 7), (0, menos 3), (1, menos 1) e (2, 3).$

6. $y=−3x$

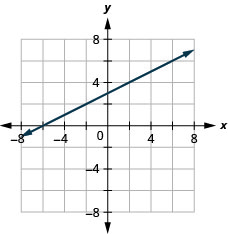
7. $y=\frac{1}{2}x+3$

Resposta: $Esta figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 6, 0), (0, 3), (2, 4) e (4, 5).$

8. $y=−\frac{4}{5}|x−1$

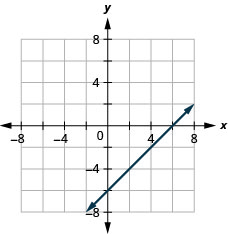
9. $x−y=6$

Resposta: $Esta figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 1, menos 7), (0, menos 6), (3, menos 3) e (6, 0).$

10. $2x+y=7$

11. $3x−2y=6$

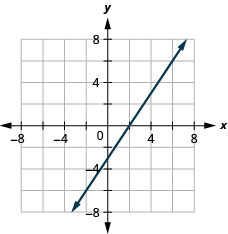
Resposta: $Esta figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 2, menos 6), (0, menos 3), (2, 0) e (4, 3).$

Gráfico de linhas verticais e horizontais

Nos exercícios a seguir, represente graficamente cada equação.

12. $y=−2$

13. $x=3$

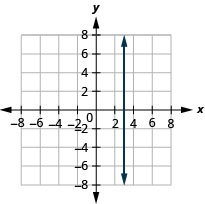
Resposta: $Esta figura mostra uma linha reta vertical representada graficamente no plano da coordenada x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (3, menos 1), (3, 0) e (3, 1).$

Nos exercícios a seguir, represente graficamente cada par de equações no mesmo sistema de coordenadas retangulares.

14. $y=−2x$e$y=−2$

15. $y=\frac{4}{3}x$e$y=\frac{4}{3}$

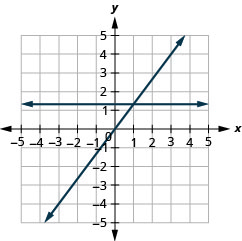
Resposta: $A figura mostra os gráficos de uma linha reta horizontal e uma linha reta inclinada no mesmo plano de coordenadas x y. Os eixos x e y vão de menos 5 a 5. A linha horizontal passa pelos pontos (0, 4 dividido por 3), (1, 4 dividido por 3) e (2, 4 dividido por 3). A linha inclinada passa pelos pontos (0, 0), (1, 4 dividido por 3) e (2, 8 dividido por 3).$

Encontre interceptações x e y

Nos exercícios a seguir, encontre as interceptações x e y.

16.
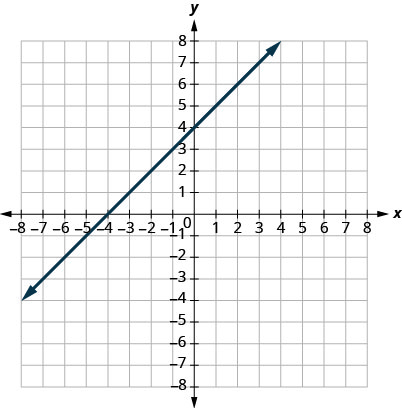
$A figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 6, menos 2), (menos 4, 0), (menos 2, 2), (0, 4), (2, 6) e (4, 8).$

17.
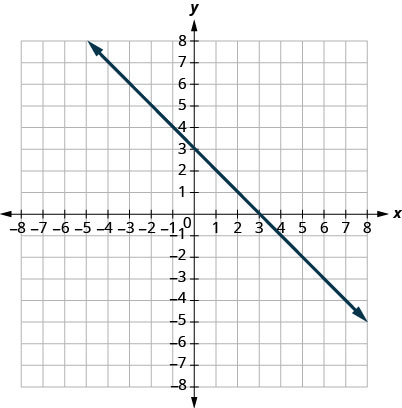
$A figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 2, 5), (menos 1, 4), (0, 3), (3, 0) e (6, menos 3).$

Resposta: $(0,3)(3,0)$

Nos exercícios a seguir, encontre os interceptos de cada equação.

18. $x−y=−1$

19. $x+2y=6$

Resposta: $(6,0),\space (0,3)$

20. $2x+3y=12$

21. $y=\frac{3}{4}x−12$

Resposta: $(16,0),\space (0,−12)$

22. $y=3x$

Representar graficamente uma linha usando as interceptações

Nos exercícios a seguir, faça um gráfico usando os interceptos.

23. $−x+3y=3$

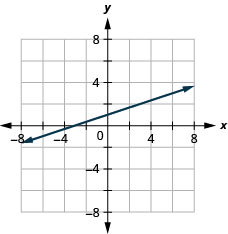
Resposta: $A figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 3, 0), (0, 1), (3, 2) e (6, 3).$

24. $x−y=4$

25. $2x−y=5$

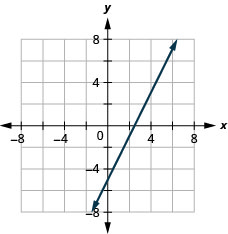
Resposta: $A figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (0, menos 5), (1, menos 3), (2, menos 1) e (3, 1).$

26. $2x−4y=8$

27. $y=4x$

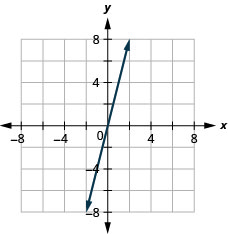
Resposta: $A figura mostra uma linha reta representada graficamente no plano de coordenadas x y. Os eixos x e y vão de menos 8 a 8. A linha passa pelos pontos (menos 1, 4), (0, 0) e (1, menos 4).$

Inclinação de uma linha

Encontre a inclinação de uma linha

Nos exercícios a seguir, encontre a inclinação de cada linha mostrada.

28.
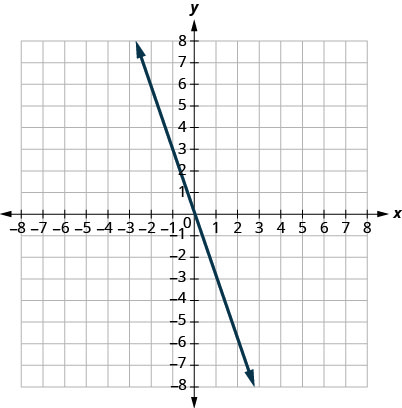
$Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha passa pelos pontos (0, 0) e (1, menos 3).$

29.
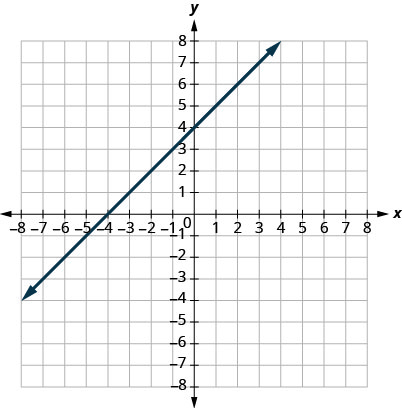
$Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha passa pelos pontos (menos 4, 0) e (0, 4).$

Resposta: 1

30.
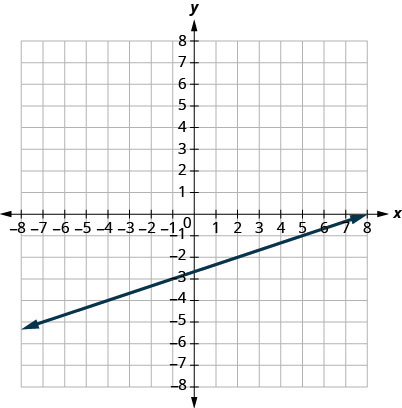
$Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha passa pelos pontos (menos 4, menos 4) e (2, menos 2).$

31.
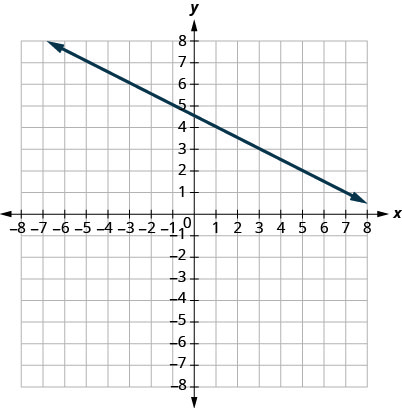
$Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha passa pelos pontos (1, 4) e (5, 2).$

Resposta: $−12$

Nos exercícios a seguir, encontre a inclinação de cada linha.

32. $y=2$

33. $x=5$

Resposta: indefinida

34. $x=−3$

35. $y=−1$

Resposta: 0

Use a fórmula de inclinação para encontrar a inclinação de uma linha entre dois pontos

Nos exercícios a seguir, use a fórmula da inclinação para encontrar a inclinação da linha entre cada par de pontos.

36. $(−1,−1),(0,5)$

37. $(3.5),(4,−1)$

Resposta: $−6$

38. $(−5,−2),(3,2)$

39. $(2,1),(4,6)$

Resposta: $52$

Representar graficamente uma linha com um ponto e a inclinação

Nos exercícios a seguir, represente graficamente cada linha com o ponto e a inclinação fornecidos.

40. $(2,−2);\space m=52$

41. $(−3,4);\space m=−13$

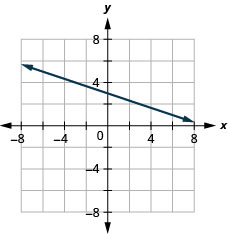
Resposta: $Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 8 a 8. O eixo y vai de menos 8 a 8. A linha passa pelos pontos (menos 3, 4) e (0, 3).$

42. $x$-interceptar$−4; m=3$

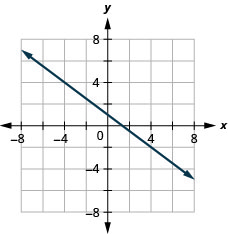
43. $y$-interceptar$1; m=−34$

Resposta: $Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 8 a 8. O eixo y vai de menos 8 a 8. A linha passa pelos pontos (0, 1) e (4, menos 2).$

Representar graficamente uma linha usando sua inclinação e interceptação

Nos exercícios a seguir, identifique a inclinação e a$y$ interceptação de cada linha.

44. $y=−4x+9$

45. $y=53x−6$

Resposta: $m=53;\space (0,−6)$

46. $5x+y=10$

47. $4x−5y=8$

Resposta: $m=\frac{4}{5};\space (0,−\frac{8}{5})$

Nos exercícios a seguir, represente graficamente a linha de cada equação usando sua inclinação e intercepto y.

48. $y=2x+3$

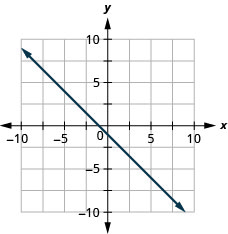
49. $y=−x−1$

Resposta: $Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (0, menos 1) e (1, menos 2).$

50. $y=−25x+3$

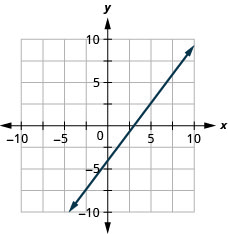
51. $4x−3y=12$

Resposta: $Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (0, menos 4) e (3, 0).$

Nos exercícios a seguir, determine o método mais conveniente para representar graficamente cada linha.

52. $x=5$

53. $y=−3$

Resposta: linha horizontal

54. $2x+y=5$

55. $x−y=2$

Resposta: intercepta

56. $y=22x+2$

57. $y=34x−1$

Resposta: pontos de plotagem

Aplicações gráficas e de interpretação do Slope-Intercept

58. Katherine é chef particular. A equação$C=6.5m+42$ modela a relação entre seu custo semanal, C, em dólares e o número de refeições, m, que ela serve.

ⓐ Descubra o custo de Katherine por uma semana quando ela não serve refeições.
ⓑ Encontre o custo de uma semana quando ela serve 14 refeições.
ⓒ Interprete a inclinação e a interceptação C da equação.
ⓓ Faça um gráfico da equação.

59. Marjorie ensina piano. A equação$P=35h−250$ modela a relação entre seu lucro semanal, P, em dólares e o número de aulas, s, que ela ensina.

ⓐ Descubra o lucro de Marjorie por uma semana quando ela não dá aulas para alunos.
ⓑ Encontre o lucro de uma semana quando ela dá aulas para 20 alunos.
ⓒ Interprete a inclinação e o intercepto P da equação.
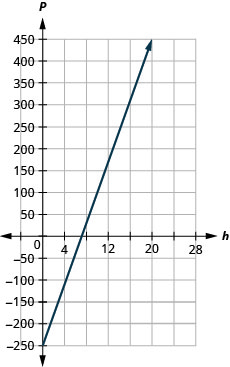
ⓓ Faça um gráfico da equação.

Resposta

ⓐ$−$250$
ⓑ$$450$
ⓒ A inclinação, 35, significa que o lucro semanal de Marjorie, P, aumenta em $35 para cada aula adicional que ela ensina.
O intercepto P significa que quando o número de aulas é 0, Marjorie perde $250.
ⓓ

$Esta figura mostra o gráfico de uma linha reta no plano de coordenadas x y. O eixo x vai de menos 4 a 28. O eixo y vai de menos 250 a 450. A linha passa pelos pontos (0, menos 250) e (20.450).$

Use inclinações para identificar linhas paralelas e perpendiculares

Nos exercícios a seguir, use inclinações e$y$ interceptos para determinar se as linhas são paralelas, perpendiculares ou nenhuma delas.

60. $4x−3y=−1;\quad y=43x−3$

61. $y=5x−1;\quad 10x+2y=0$

Resposta: nem

62. $3x−2y=5;\quad 2x+3y=6$

63. $2x−y=8;\quad x−2y=4$

Resposta: não paralelo

Encontre a equação de uma reta

Encontre uma equação da reta dada a inclinação e a interceptação y

Nos exercícios a seguir, encontre a equação de uma reta com determinada inclinação e intercepto y. Escreva a equação na forma inclinação-interceptação.

64. Inclinação$\frac{1}{3}$ e$y$ interceptação$(0,−6)$

65. Inclinação$−5$ e$y$ interceptação$(0,−3)$

Resposta: $y=−5x−3$

66. Inclinação$0$ e$y$ interceptação$(0,4)$

67. Inclinação$−2$ e$y$ interceptação$(0,0)$

Resposta: $y=−2x$

Nos exercícios a seguir, encontre a equação da linha mostrada em cada gráfico. Escreva a equação na forma inclinação-interceptação.

68.
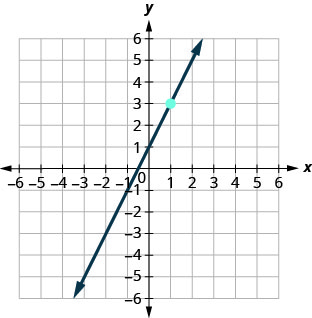
$Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, 1), (1, 3) e (2, 5).$

69.
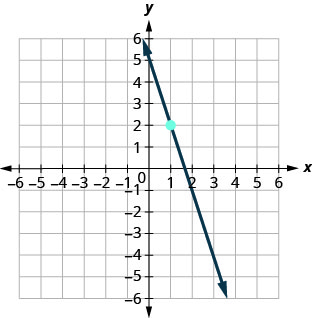
$Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, 5), (1, 2) e (2, menos 1).$

Resposta: $y=−3x+5$

70.
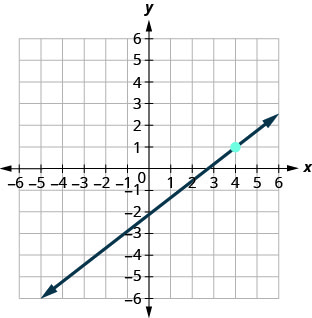
$Esta figura tem um gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, menos 2), (4, 1) e (8, 4).$

71.
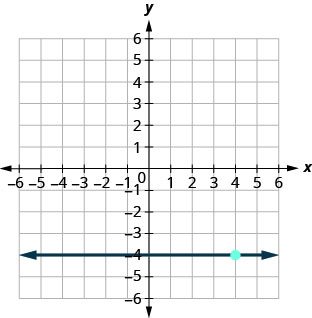
$Esta figura tem um gráfico de uma linha reta horizontal no plano de coordenadas x y. Os eixos x e y vão de menos 10 a 10. A linha passa pelos pontos (0, menos 4), (1, menos 4) e (2, menos 4).$

Resposta: $y=−4$

Encontre uma equação da reta dada a inclinação e um ponto

Nos exercícios a seguir, encontre a equação de uma reta com determinada inclinação e contendo o ponto dado. Escreva a equação na forma inclinação-interceptação.

72. $m=−\frac{1}{4}$, ponto$(−8,3)$

73. $m=\frac{3}{5}$, ponto$(10,6)$

Resposta: $y=\frac{3}{5}x$

74. Linha horizontal contendo$(−2,7)$

75. $m=−2$, ponto$(−1,−3)$

Resposta: $y=−2x−5$

Encontre uma equação da reta dados dois pontos

Nos exercícios a seguir, encontre a equação de uma linha contendo os pontos dados. Escreva a equação na forma inclinação-interceptação.

76. $(2,10)$e$(−2,−2)$

77. $(7,1)$e$(5,0)$

Resposta: $y=\frac{1}{2}x−\frac{5}{2}$

78. $(3,8)$e$(3,−4)$

79. $(5,2)$e$(−1,2)$

Resposta: $y=2$

Encontre uma equação de uma reta paralela a uma determinada linha

Nos exercícios a seguir, encontre uma equação de uma reta paralela à linha dada e contenha o ponto dado. Escreva a equação na forma inclinação-interceptação.

80. linha$y=−3x+6$, ponto$(1,−5)$

81. linha$2x+5y=−10$, ponto$(10,4)$

Resposta: $y=−\frac{2}{5}x+8$

82. linha$x=4$, ponto$(−2,−1)$

83. linha$y=−5$, ponto$(−4,3)$

Resposta: $y=3$

Encontre uma equação de uma reta perpendicular a uma determinada linha

Nos exercícios a seguir, encontre uma equação de uma reta perpendicular à linha dada e contenha o ponto dado. Escreva a equação na forma inclinação-interceptação.

84. linha$y=−\frac{4}{5}x+2$, ponto$(8,9)$

85. linha$2x−3y=9$, ponto$(−4,0)$

Resposta: $y=−\frac{3}{2}x−6$

86. linha$y=3$, ponto$(−1,−3)$

87.$x=−5$ ponto de linha$(2,1)$

Resposta: $y=1$

Gráfico de desigualdades lineares em duas variáveis

Verificar soluções para uma desigualdade em duas variáveis

Nos exercícios a seguir, determine se cada par ordenado é uma solução para a desigualdade dada.

88. Determine se cada par ordenado é uma solução para a desigualdade$y<x−3$:

ⓐ$(0,1)$ ⓑ$(−2,−4)$ ⓒ$(5,2)$ ⓓ$(3,−1)$
ⓔ$(−1,−5)$

89. Determine se cada par ordenado é uma solução para a desigualdade$x+y>4$:

ⓐ$(6,1)$ ⓑ$(−3,6)$ ⓒ$(3,2)$ ⓓ$(−5,10)$ ⓔ$(0,0)$

Resposta: ⓐ sim ⓑ não ⓒ sim ⓓ sim; ⓔ nom

Reconhecer a relação entre as soluções de uma desigualdade e seu gráfico

Nos exercícios a seguir, escreva a desigualdade mostrada pela região sombreada.

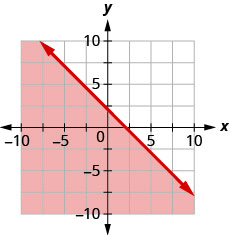
90. Escreva a desigualdade mostrada pelo gráfico com a linha limite$y=−x+2.$

$Esta figura tem o gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. Uma linha é desenhada através dos pontos (0, 2), (1, 1) e (2, 0). A linha divide o plano da coordenada x y em duas metades. A linha e a metade inferior esquerda estão sombreadas em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

91. Escreva a desigualdade mostrada pelo gráfico com a linha limite$y=\frac{2}{3}x−3$.

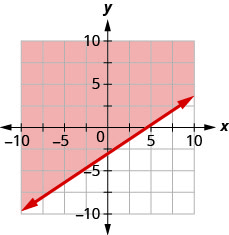
$Esta figura tem o gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. Uma linha é traçada através dos pontos (0, menos 3), (3, menos 1) e (6, 1). A linha divide o plano da coordenada x y em duas metades. A linha e a metade superior esquerda estão sombreadas em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

Resposta: $y>\frac{2}{3}x−3$

92. Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite$x+y=−4$.

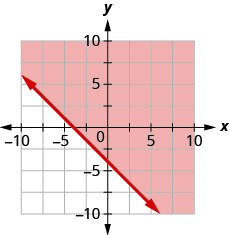
$Esta figura tem o gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. Uma linha é traçada através dos pontos (0, menos 4), (menos 2, menos 2) e (menos 4, 0). A linha divide o plano da coordenada x y em duas metades. A linha e a metade superior direita estão sombreadas em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

93. Escreva a desigualdade mostrada pela região sombreada no gráfico com a linha limite$x−2y=6$.

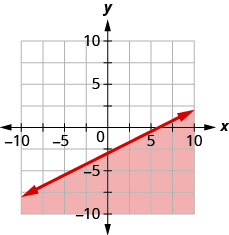
$Esta figura tem o gráfico de uma linha reta no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. Uma linha é traçada através dos pontos (0, menos 3), (2, menos 2) e (6, 0). A linha divide o plano da coordenada x y em duas metades. A linha e a metade inferior direita estão sombreadas em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

Resposta: $x−2y\geq 6$

Gráfico de desigualdades lineares em duas variáveis

Nos exercícios a seguir, represente graficamente cada desigualdade linear.

94. Representar graficamente a desigualdade linear$y>\frac{2}{5}x−4$.

95. Representar graficamente a desigualdade linear$y\leq −\frac{1}{4}x+3$.

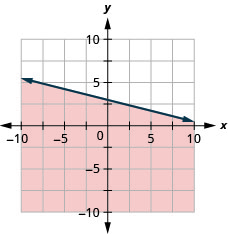
Resposta: $Esta figura tem o gráfico de uma linha reta tracejada no plano de coordenadas x y. Os eixos x e y vão de menos 10 a 10. Uma linha reta tracejada é desenhada através dos pontos (0, 3), (4, 2) e (8, 1). A linha divide o plano da coordenada x y em duas metades. A metade inferior esquerda está sombreada em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

96. Representar graficamente a desigualdade linear$x−y\leq 5$.

97. Representar graficamente a desigualdade linear$3x+2y>10.$

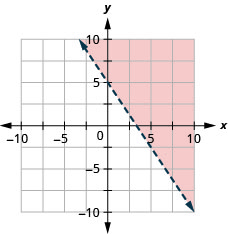
Resposta: $Esta figura tem o gráfico de uma linha reta tracejada no plano de coordenadas x y. Os eixos x e y vão de menos 10 a 10. Uma linha reta tracejada é desenhada através dos pontos (0, 5), (2, 2) e (4, menos 1). A linha divide o plano da coordenada x y em duas metades. A metade superior direita está sombreada em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

98. Representar graficamente a desigualdade linear$y\leq −3x$.

99. Representar graficamente a desigualdade linear$y<6.$

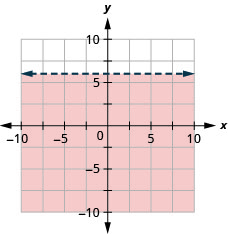
Responda: $Esta figura tem o gráfico de uma linha tracejada horizontal reta no plano de coordenadas x y. Os eixos x e y vão de menos 10 a 10. Uma linha reta tracejada é desenhada através dos pontos (0, 6), (1, 6) e (2, 6). A linha divide o plano da coordenada x y em duas metades. A metade inferior está sombreada em vermelho para indicar que é aqui que estão as soluções da desigualdade.$

Resolva aplicativos usando desigualdades lineares em duas variáveis

100. Shanthie precisa ganhar pelo menos $500 por semana durante as férias de verão para pagar a faculdade. Ela trabalha em dois empregos. Um como instrutor de natação que paga $10 por hora e o outro como estagiário em um escritório de advocacia por $25 horas. Quantas horas Shanthie precisa trabalhar em cada emprego para ganhar pelo menos $500 por semana?

ⓐ Seja x o número de horas que ela trabalha ensinando natação e que y seja o número de horas que ela trabalha como estagiária. Escreva uma desigualdade que modelaria essa situação.
ⓑ Faça um gráfico da desigualdade.
ⓒ Encontre três pares ordenados$(x,y)$ que seriam soluções para a desigualdade. Em seguida, explique o que isso significa para Shanthie.

101. Atsushi, ele precisa se exercitar o suficiente para queimar$600$ calorias todos os dias. Ele prefere correr ou andar de bicicleta e queima$20$ calorias por minuto enquanto corre e$15$ calorias por minuto enquanto anda de bicicleta.

ⓐ Se x é o número de minutos que Atsushi corre e y é o número de minutos que ele anda de bicicleta, encontre a desigualdade que modela a situação.
ⓑ Faça um gráfico da desigualdade.
ⓒ Liste três soluções para a desigualdade. Quais opções as soluções oferecem ao Atsushi?

Responda

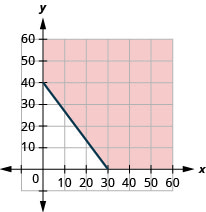
ⓐ$20x+15y\geq 60020x+15y\geq 600$
ⓑ

$A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 50. O eixo y vai de 0 a 50. A linha passa pelos pontos (0, 40) e (30, 0). A linha divide o plano coordenado em duas metades. A metade superior direita e a linha são coloridas em vermelho para indicar que esse é o conjunto de soluções.$

Relações e funções

Encontre o domínio e o alcance de uma relação

Nos exercícios a seguir, para cada relação, ⓐ encontre o domínio da relação ⓑ encontre o alcance da relação.

102. ${\{(5,−2),\,(5,−4),\,(7,−6),\,(8,−8),\,(9,−10)}\}$

103. ${\{(−3,7),\,(−2,3),\,(−1,9), \,(0,−3),\,(−1,8)}\}$

Responda: ⓐ$D: {−3, −2, −1, 0}$
ⓑ$R: {7, 3, 9, −3, 8}$

No exercício a seguir, use o mapeamento da relação para ⓐ listar os pares ordenados da relação ⓑ encontre o domínio da relação ⓒ encontre o intervalo da relação.

104. O mapeamento abaixo mostra o peso médio de uma criança de acordo com a idade.

$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “Idade (anos)” e lista os números 1, 2, 3, 4, 5, 6 e 7. A tabela à direita tem o cabeçalho “Peso (libras)” e lista os números 20, 35, 30, 45, 40, 25 e 50. Há setas começando com números na tabela de idade e apontando para números na tabela de peso. A primeira flecha vai de 1 a 20. A segunda flecha vai de 2 a 25. A terceira flecha vai de 3 a 30. A quarta flecha vai de 4 a 35. A quinta flecha vai de 5 a 40. A sexta flecha vai de 6 a 45. A sétima flecha vai de 7 a 50.$

No exercício a seguir, use o gráfico da relação para ⓐ listar os pares ordenados da relação ⓑ encontre o domínio da relação ⓒ encontre o intervalo da relação.

105.
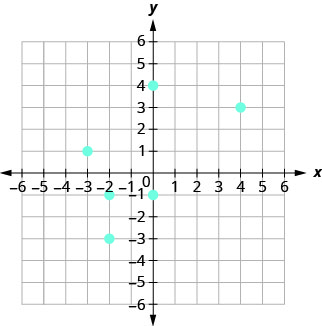
$A figura mostra o gráfico de alguns pontos no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. Os pontos (menos 3, 1), (menos 2, menos 1), (menos 2, menos 3), (0, menos 1), (0, 4) e (4, 3).$

Responda: ⓐ$(4, 3), \,(−2, −3), \,(−2, −1), \,(−3, 1), \,(0, −1), \,(0, 4)$
ⓑ$D: {−3, −2, 0, 4}$
ⓒ$R: {−3, −1, 1, 3, 4}$

Determine se uma relação é uma função

Nos exercícios a seguir, use o conjunto de pares ordenados para ⓐ determinar se a relação é uma função ⓑ encontre o domínio da relação ⓒ encontre o alcance da relação.

106. ${\{(9,−5),\,(4,−3),\,(1,−1),\,(0,0),\,(1,1),\,(4,3),\,(9,5)}\}$

107. ${\{(−3,27),\,(−2,8),\,(−1,1),\,(0,0),\,(1,1),\,(2,8),\,(3,27)}\}$

Responda: ⓐ sim ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${0, 1, 8, 27}$

Nos exercícios a seguir, use o mapeamento para ⓐ determinar se a relação é uma função ⓑ encontre o domínio da função ⓒ encontre o alcance da função.

108.
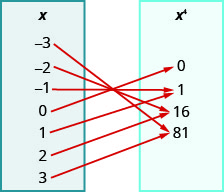
$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “x” e lista os números menos 3, menos 2, menos 1, 0, 1, 2 e 3. A tabela à direita tem o cabeçalho “x elevado à quarta potência” e lista os números 0, 1, 16 e 81. Há setas começando com números na tabela x e apontando para números no x até a quarta tabela de potência. A primeira flecha vai de menos 3 a 81. A segunda seta vai de menos 2 a 16. A terceira seta vai de menos 1 a 1. A quarta seta vai de 0 a 0. A quinta flecha vai de 1 a 1. A sexta flecha vai de 2 a 16. A sétima flecha vai de 3 a 81.$

109.
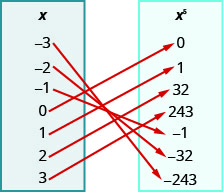
$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “x” e lista os números menos 3, menos 2, menos 1, 0, 1, 2 e 3. A tabela à direita tem o cabeçalho “x elevado à quinta potência” e lista os números 0, 1, 32, 243, menos 1, menos 32 e menos 243. Há setas começando com números na tabela x e apontando para números na tabela x até a quinta tabela de potência. A primeira seta vai de menos 3 para menos 243. A segunda seta vai de menos 2 para menos 32. A terceira seta vai de menos 1 a 1. A quarta seta vai de 0 a 0. A quinta flecha vai de 1 a 1. A sexta flecha vai de 2 a 32. A sétima flecha vai de 3 a 243.$

Responda: ⓐ${−3, −2, −1, 0, 1, 2, 3}$
ⓑ${−3, −2, −1, 0, 1, 2, 3}$
ⓒ${−243, −32, −1, 0, 1, 32, 243}$

Nos exercícios a seguir, determine se cada equação é uma função.

110. $2x+y=−3$

111. $y=x^2$

Responda: sim

112. $y=3x−5$

113. $y=x^3$

Responda: sim

114. $2x+y2=4$

Encontre o valor de uma função

Nos exercícios a seguir, avalie a função:

ⓐ$f(−2)$ ⓑ$f(3)$ ⓒ$f(a)$.

115. $f(x)=3x−4$

Responda: ⓐ$f(−2)=−10$ ⓑ$f(3)=5$ ⓒ$f(a)=3a−4$

116. $f(x)=−2x+5$

117. $f(x)=x^2−5x+6$

Responda: ⓐ$f(−2)=20$ ⓑ$f(3)=0$ ⓒ$f(a)=a^2−5a+6$

118. $f(x)=3x^2−2x+1$

Nos exercícios a seguir, avalie a função.

119. $g(x)=3x2−5x;\space g(2)$

Responda: $2$

120. $F(x)=2x2−3x+1;\space F(−1)$

121. $h(t)=4|t−1|+2;\space h(t)=4$

Responda: $18$

122. $f(x)=x+2x−1;\space f(3)$

Gráficos de funções

Use o teste de linha vertical

Nos exercícios a seguir, determine se cada gráfico é o gráfico de uma função.

123.
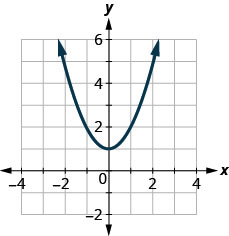
$A figura tem uma função quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A parábola passa pelos pontos (menos 2, 5), (menos 1, 2), (0, 1), (1, 2) e (2, 5). O ponto mais baixo do gráfico é (0, 1).$

Responda: sim

124.
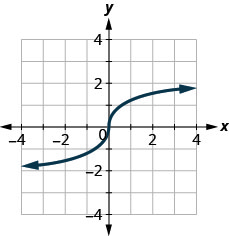
$A figura tem uma função em forma de s representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A curva passa pelos pontos (menos 1, menos 1), (0, 0) e (1, 1).$

125.
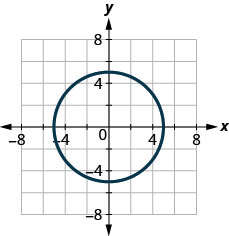
$A figura tem um círculo representado graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. O círculo passa pelos pontos (menos 5, 0), (5, 0), (0, menos 5) e (0, 5).$

Responda: não

126.
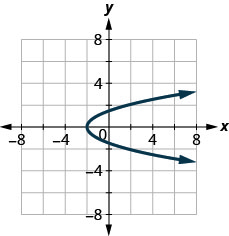
$A figura tem uma abertura de parábola à direita representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A parábola passa pelos pontos (menos 2, 0), (menos 1, 1), (menos 1, menos 1), (2, 2) e (2, menos 2). O ponto mais à esquerda no gráfico é (menos 2, 0).$

127.
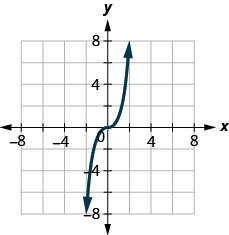
$A figura tem uma função de cubo representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva passa pelos pontos (menos 1, menos 1), (0, 0) e (1, 1).$

Responda: sim

128.
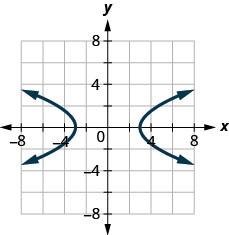
$A figura tem duas linhas curvas representadas graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva à esquerda passa pelos pontos (menos 3, 0), (menos 4, 2) e (menos 4, menos 2). A linha curva à direita passa pelos pontos (3, 0), (4, 2) e (4, menos 2).$

129.
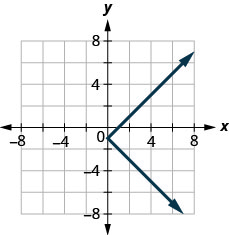
$A figura tem uma função de valor absoluto lateral representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha se curva no ponto (0, menos 1) e vai para a direita. A linha passa pelos pontos (1, 0), (1, menos 2), (2, 1) e (2, menos 3).$

Responda: não

Identifique gráficos de funções básicas

Nos exercícios a seguir, ⓐ represente graficamente cada função ⓑ declare seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo.

130. $f(x)=5x+1$

131. $f(x)=−4x−2$

Responda

ⓐ

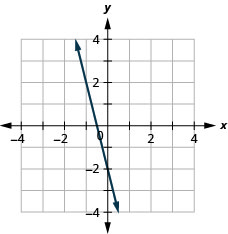
$A figura tem uma função linear representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha passa pelos pontos (menos 2, 6), (menos 1, 2) e (0, menos 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

132. $f(x)=\frac{2}{3}x−1$

133. $f(x)=−6$

Responda

ⓐ

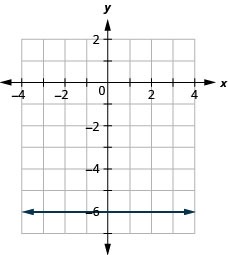
$A figura tem uma função constante representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 8 a 4. A linha passa pelos pontos (0, menos 6), (1, menos 6) e (2, menos 6).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

134. $f(x)=2x$

135. $f(x)=3x^2$

Responda

ⓐ

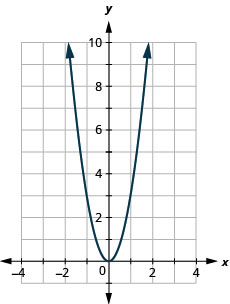
$A figura tem uma função quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A parábola passa pelos pontos (menos 1, 3), (0, 0) e (1, 3). O ponto mais baixo do gráfico é (0, 0).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,0]$

136. $f(x)=−12x^2$

137. $f(x)=x^2+2$

Responda

ⓐ

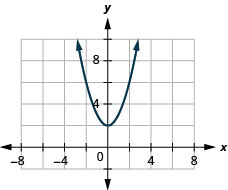
$A figura tem uma função quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 4 a 8. A parábola passa pelos pontos (menos 2, 6), (menos 1, 3), (0, 2), (1, 3) e (2, 6). O ponto mais baixo do gráfico é (0, 2).$

ⓑ$D: (-\inf ,\inf ), R: (-\inf ,\inf )$

138. $f(x)=x^3−2$

139. $f(x)=\sqrt{x+2}$

Responda

ⓐ

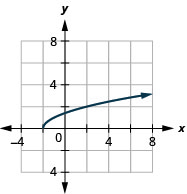
$A figura tem uma função de raiz quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 4 a 8. O eixo y vai de menos 2 a 10. A meia linha começa no ponto (menos 2, 0) e passa pelos pontos (menos 1, 1) e (2, 2).$

ⓑ$D: [−2,−2, \inf ), \space R: [0,\inf )$

140. $f(x)=−|x|$

141. $f(x)=|x|+1$

Responda

ⓐ

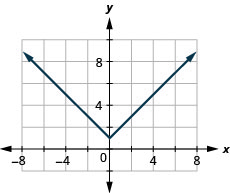
$A figura tem uma função de valor absoluto representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. O vértice está no ponto (0, 1). A linha passa pelos pontos (menos 1, 2) e (1, 2).$

ⓑ$D: (-\inf ,\inf ), \space R: [1,\inf )$

Leia informações de um gráfico de uma função

Nos exercícios a seguir, use o gráfico da função para encontrar seu domínio e alcance. Escreva o domínio e o intervalo em notação de intervalo

142.
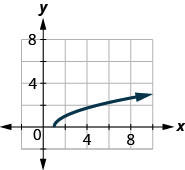
$A figura tem uma função de raiz quadrada representada graficamente no plano da coordenada x y. O eixo x vai de 0 a 10. O eixo y vai de 0 a 10. A meia linha começa no ponto (1, 0) e passa pelos pontos (2, 1) e (5, 2).$

143.
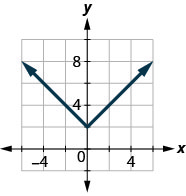
$A figura tem uma função de valor absoluto representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. O vértice está no ponto (0, 2). A linha passa pelos pontos (menos 1, 3) e (1, 3).$

Responda: $D: (-\inf ,\inf ), R: [2,\inf )$

144.
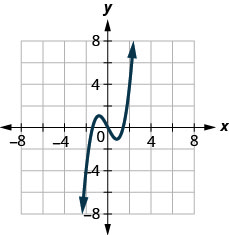
$A figura tem uma função cúbica representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva passa pelos pontos (menos 2, menos 4), (0, 0) e (2, 4).$

Nos exercícios a seguir, use o gráfico da função para encontrar os valores indicados.

145.
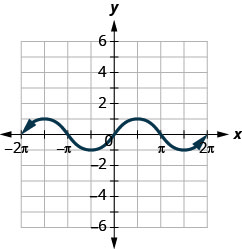
$Esta figura tem uma linha curva ondulada representada graficamente no plano de coordenadas x y. O eixo x vai de menos 2 vezes pi a 2 vezes pi. O eixo y vai de menos 6 a 6. O segmento de linha curva passa pelos pontos (menos 2 vezes pi, 0), (menos 3 dividido por 2 vezes pi, 1), (pi negativo, 0), (menos 1 dividido por 2 vezes pi, negativo 1), (0, 0), (1 dividido por 2 vezes pi, 1), (pi, 0), (3 dividido por 2 vezes pi, menos 1) e (2 vezes pi, 0). Os pontos (menos 3 dividido por 2 vezes pi, 1) e (1 dividido por 2 vezes pi, 1) são os pontos mais altos no gráfico. Os pontos (menos 1 dividido por 2 vezes pi, menos 1) e (3 dividido por 2 vezes pi, menos 1) são os pontos mais baixos do gráfico. O padrão se estende infinitamente para a esquerda e para a direita.$

ⓐ Encontre$f(0)$.
ⓑ Encontre$f(12\pi )$.
ⓒ Encontre$f(−32\pi )$.
ⓓ Encontre os valores para$x$ quando$f(x)=0$.
ⓔ Encontre as$x$ interceptações.
ⓕ Encontre o (s)$y$ intercepto (s).
ⓖ Encontre o domínio. Escreva em notação de intervalo.
ⓗ Encontre o alcance. Escreva em notação de intervalo.

Responda: ⓐ$f(x)=0$ ⓑ$f(\pi /2)=1$
ⓒ$f(−3\pi /2)=1$ ⓓ$f(x)=0$ para$x=−2\pi ,−\pi ,0,\pi ,2\pi$
ⓔ$(−2\pi ,0), (−\pi ,0), (0,0), (\pi ,0), (2\pi ,0)$ ⓕ$(0,0)$
ⓖ$[−2\pi ,2\pi ]$ ⓗ$[−1,1]$

146.
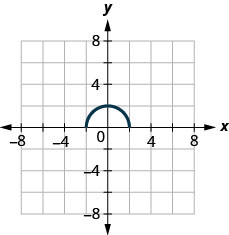
$A figura tem um semicírculo representado graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. O segmento da linha curva começa no ponto (menos 2, 0). A linha passa pelo ponto (0, 2) e termina no ponto (2, 0). O ponto (0, 2) é o ponto mais alto do gráfico.$

ⓐ Encontre$f(0)$.
ⓑ Encontre os valores para$x$ quando$f(x)=0$.
ⓒ Encontre as$x$ interceptações.
ⓓ Encontre o (s)$y$ intercepto (s).
ⓔ Encontre o domínio. Escreva em notação de intervalo.
ⓕ Encontre o alcance. Escreva em notação de intervalo.

Teste prático

1. Faça um gráfico de cada ponto em um sistema de coordenadas retangular.

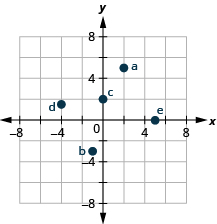
Responda: $Esta figura mostra os pontos traçados no plano da coordenada x y. Os eixos x e y vão de menos 10 a 10. O ponto rotulado a está 2 unidades à direita da origem e 5 unidades acima da origem e está localizado no quadrante I. O ponto rotulado b está 1 unidade à esquerda da origem e 3 unidades abaixo da origem e está localizado no quadrante III. O ponto rotulado c está 2 unidades acima da origem e está localizado no eixo y. O ponto identificado como d está 4 unidades à esquerda da origem e 1,5 unidades acima da origem e está localizado no quadrante II. O ponto rotulado e está 5 unidades à direita da origem e está localizado no eixo x.$

2. Quais dos pares ordenados fornecidos são soluções para a equação$3x−y=6$?

3. Encontre a inclinação de cada linha mostrada.

ⓐ

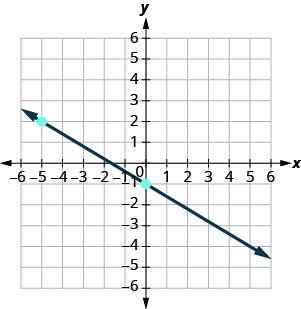
$A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 5, 2) (0, menos 1) e (5, menos 4).$

ⓑ

$A figura tem uma linha reta vertical representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (2, 0) (2, menos 1) e (2, 1).$

Responda: ⓐ$−\frac{3}{5}$ ⓑ indefinido

4. Encontre a inclinação da linha entre os pontos$(5,2)$$(−1,−4)$ e.

5. Faça um gráfico da linha com a inclinação$\frac{1}{2}$ contendo o ponto$(−3,−4)$.

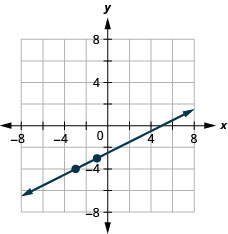
Responda: $A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 3, menos 4) (menos 1, menos 3) e (1, menos 2).$

6. Encontre as interceptações$4x+2y=−8$ e o gráfico.

Faça um gráfico da linha para cada uma das equações a seguir.

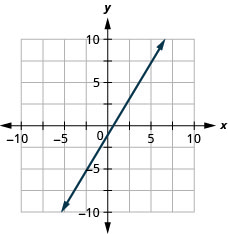
7. $y=\frac{5}{3}x−1$

Responda: $A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 3, menos 6) (0, menos 1) e (3, 4).$

8. $y=−x$

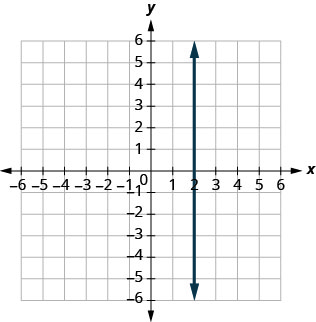
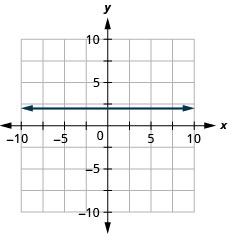
9. $y=2$

Responda: $A figura tem uma linha reta horizontal representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 1, 2) (0, 2) e (1, 2).$

Encontre a equação de cada linha. Escreva a equação na forma de interceptação de inclinação.

10. inclinação$−\frac{3}{4}$ e$y$ interceptação$(0,−2)$

11. $m=2$, ponto$(−3,−1)$

Responda: $y=2x+5$

12. contendo$(10,1)$ e$(6,−1)$

13. perpendicular à linha$y=\frac{5}{4}x+2$, contendo o ponto$(−10,3)$

Responda: $y=−\frac{4}{5}x−5$

14. Escreva a desigualdade mostrada pelo gráfico com a linha limite$y=−x−3$.

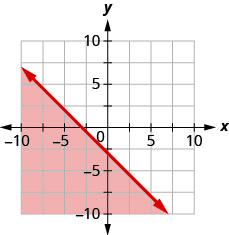
$A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 3, 0), (0, menos 3) e (1, menos 4). A linha divide o plano coordenado em duas metades. A metade inferior esquerda e a linha são coloridas em vermelho para indicar que esse é o conjunto de soluções.$

Representar graficamente cada desigualdade linear.

15. $y>\frac{3}{2}x+5$

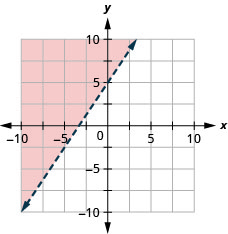
Responda: $A figura tem uma linha reta tracejada representada graficamente no plano de coordenadas x y. O eixo x vai de menos 10 a 10. O eixo y vai de menos 10 a 10. A linha passa pelos pontos (menos 2, 2), (0, 5) e (2, 8). A linha divide o plano coordenado em duas metades. A metade superior esquerda é colorida em vermelho para indicar que esse é o conjunto de soluções.$

16. $x−y\geq −4$

17. $y\leq −5x$

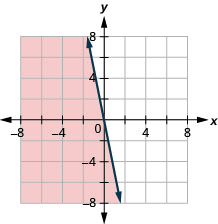
Responda: $A figura tem uma linha reta representada graficamente no plano da coordenada x y. O eixo x vai de menos 8 a 8. O eixo y vai de menos 8 a 8. A linha passa pelos pontos (menos 1, 5), (0, 0) e (1, menos 5). A linha divide o plano coordenado em duas metades. A metade inferior esquerda e a linha são coloridas em vermelho para indicar que esse é o conjunto de soluções.$

18. Hiro trabalha em dois empregos de meio período para ganhar dinheiro suficiente para cumprir suas obrigações de pelo menos $450 por semana. Seu trabalho no shopping paga $10 por hora e seu trabalho de assistente administrativa no campus paga $15 por hora. Quantas horas Hiro precisa trabalhar em cada emprego para ganhar pelo menos $450?

ⓐ Seja x o número de horas que ela trabalha no shopping e que y seja o número de horas que ela trabalha como assistente administrativa. Escreva uma desigualdade que modelaria essa situação.
ⓑ Faça um gráfico da desigualdade.
ⓒ Encontre três pares ordenados$(x,y)$ que seriam soluções para a desigualdade. Em seguida, explique o que isso significa para Hiro.

19. Use o conjunto de pares ordenados para ⓐ determinar se a relação é uma função, ⓑ encontrar o domínio da relação e ⓒ encontrar o alcance da relação.

\ ({\ {(−3,27), (−2,8), (−1,1), (0,0),
(1,1), (2,8), (3,27)}\}\)

$f(x)=4x^2−2x−3$

21. Para$h(y)=3|y−1|−3$, avalie$h(−4)$.

Responda: $12$

22. Determine se o gráfico é o gráfico de uma função. Explique sua resposta.

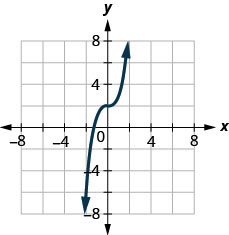
$A figura tem uma função de cubo representada graficamente no plano de coordenadas x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A linha curva passa pelos pontos (menos 1, 1), (0, 2) e (1, 3).$

Nos exercícios a seguir, ⓐ represente graficamente cada função ⓑ declare seu domínio e alcance.
Escreva o domínio e o intervalo em notação de intervalo.

23. $f(x)=x^2+1$

Responda

ⓐ

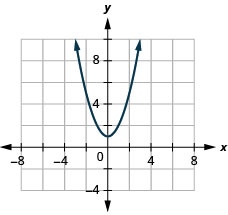
$A figura tem uma função quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 2 a 10. A parábola passa pelos pontos (menos 2, 5), (menos 1, 2), (0, 1), (1, 2) e (2, 5). O ponto mais baixo do gráfico é (0, 1).$

ⓑ$D: (-\inf ,\inf ), R: [1,\inf )$

24. $f(x)=\sqrt{x+1}$

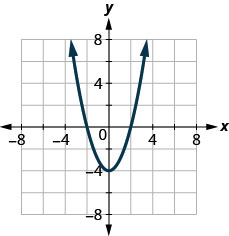
$A figura tem uma função quadrada representada graficamente no plano da coordenada x y. O eixo x vai de menos 6 a 6. O eixo y vai de menos 6 a 6. A parábola passa pelos pontos (menos 2, 0), (menos 1, menos 3), (0, menos 4), (1, menos 3) e (2, 0). O ponto mais baixo do gráfico é (0, menos 4).$

ⓑ Encontre as$y$ interceptações.
ⓒ Encontre$f(−1)$.
ⓓ Encontre$f(1)$.
ⓔ Encontre o domínio. Escreva em notação de intervalo.
ⓕ Encontre o alcance. Escreva em notação de intervalo.