3.6: Relações e funções

Last updated
Save as PDF

Page ID: 183127

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de

Ao final desta seção, você poderá:

Encontre o domínio e o alcance de uma relação
Determine se uma relação é uma função
Encontre o valor de uma função

Antes de começar, faça este teste de prontidão.

Avalie$3x−5$ quando$x=−2$.
Se você perdeu esse problema, revise [link].
Avalie$2x^2−x−3$ quando$x=a$.
Se você perdeu esse problema, revise [link].
Simplifique:$7x−1−4x+5$.
Se você perdeu esse problema, revise [link].

Encontre o domínio e o alcance de uma relação

À medida que seguimos nossas vidas diárias, temos muitos itens de dados ou quantidades que estão emparelhados com nossos nomes. Nosso número de previdência social, número de carteira de estudante, endereço de e-mail, número de telefone e nosso aniversário correspondem ao nosso nome. Há uma relação entre nosso nome e cada um desses itens.

Quando seu professor recebe sua lista de turmas, os nomes de todos os alunos da turma são listados em uma coluna e, em seguida, o número da carteira de estudante provavelmente estará na próxima coluna. Se pensarmos na correspondência como um conjunto de pares ordenados, onde o primeiro elemento é o nome do aluno e o segundo elemento é o número de identificação do aluno, chamamos isso de relação.

\[(\text{Student name}, \text{ Student ID #})\nonumber \]

O conjunto de todos os nomes dos alunos da turma é chamado de domínio da relação e o conjunto de todos os números de identificação estudantil emparelhados com esses alunos é o intervalo da relação.

Há muitas situações semelhantes em que uma variável é emparelhada ou combinada com outra. O conjunto de pares ordenados que registra essa correspondência é uma relação.

Definição: Relação

Uma relação é qualquer conjunto de pares ordenados,$(x,y)$. Todos os valores x nos pares ordenados juntos formam o domínio. Todos os valores de y nos pares ordenados juntos formam o intervalo.

Exemplo$\PageIndex{1}$

Para a relação${(1,1),(2,4),(3,9),(4,16),(5,25)}$:

Encontre o domínio da relação.
Encontre o alcance da relação.

Responda: \[\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}\]

Exemplo$\PageIndex{2}$

Para a relação${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$:

Encontre o domínio da relação.
Encontre o alcance da relação.

Responda a: ${\{1,2,3,4,5}\}$
Resposta b: ${\{1,8,27,64,125}\}$

Exemplo$\PageIndex{3}$

Para a relação${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$:

Encontre o domínio da relação.
Encontre o alcance da relação.

Responda a: ${\{1,2,3,4,5}\}$
Resposta b: ${\{3,6,9,12,15}\}$

MAPEAMENTO

Às vezes, um mapeamento é usado para mostrar uma relação. As setas mostram o emparelhamento dos elementos do domínio com os elementos do intervalo.

Exemplo$\PageIndex{4}$

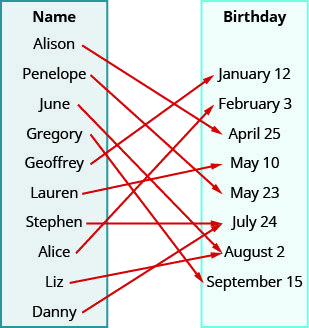
Use o mapeamento da relação mostrada com

liste os pares ordenados da relação,
encontre o domínio da relação e
encontre o alcance da relação.

$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “Nome” e lista os nomes “Alison”, “Penelope”, “June”, “Gregory”, “Geoffrey”, “Lauren”, “Stephen”, “Alice”, “Liz”, “Danny”. A tabela à direita tem o cabeçalho “Aniversário” e lista as datas “12 de janeiro”, “3 de fevereiro”, “25 de abril”, “10 de maio”, “23 de maio”, “24 de julho”, “2 de agosto” e “15 de setembro”. Há uma seta para cada nome na tabela de nomes que começa com o nome e aponta para uma data na tabela de aniversários. Embora a maioria das datas tenha apenas uma seta apontando para elas, há duas setas apontando para 24 de julho: uma de Stephen e outra de Liz.$

Responda

ⓐ A seta mostra a correspondência da pessoa com seu aniversário. Criamos pares ordenados com o nome da pessoa como valor x e sua data de nascimento como valor y.

{(Alison, 25 de abril), (Penelope, 23 de maio), (junho, 2 de agosto), (Gregory, 15 de setembro), (Geoffrey, 12 de janeiro), (Lauren, 10 de maio), (Stephen, 24 de julho), (Alice, 3 de fevereiro), (Liz, 2 de agosto), (Danny, 24 de julho)}

ⓑ O domínio é o conjunto de todos os valores x da relação.

{Alison, Penelope, June, Gregory, Geoffrey, Lauren, Stephen, Alice, Liz, Danny}

{12 de janeiro, 3 de fevereiro, 25 de abril, 10 de maio, 23 de maio, 24 de julho, 2 de agosto, 15 de setembro}

Exemplo$\PageIndex{5}$

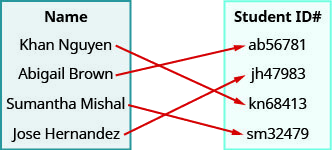
Use o mapeamento da relação mostrada com

listar os pares ordenados da relação
encontre o domínio da relação
encontre o alcance da relação.

$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “Nome” e lista os nomes “Khanh Nguyen”, “Abigail Brown”, “Sumantha Mishal” e “Jose Hern e ez”. A tabela à direita tem o cabeçalho “ID do aluno #” e lista os códigos “a b 56781”, “j h 47983”, “k n 68413” e “s m 32479”. Há uma seta para cada nome na tabela de nomes que começa com o nome e aponta para um código na tabela de identificação do aluno. A primeira flecha vai de Khanh Nguyen para k n 68413. A segunda flecha vai de Abigail Brown para a b 56781. A terceira flecha vai de Sumantha Mishal para s m 32479. A quarta seta vai de Jose Hern e ez até j h 47983.$

Responda

ⓐ (Khanh Nguyen, kn68413), (Abigail Brown, ab56781), (Sumantha Mishal, sm32479), (Jose Hern e ez, jh47983)

ⓑ {Khanh Nguyen, Abigail Brown, Sumantha Mishal, José Hern e ez}

Exemplo$\PageIndex{6}$

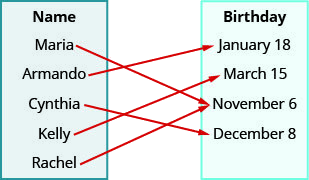
Use o mapeamento da relação mostrada com

listar os pares ordenados da relação
encontre o domínio da relação
encontre o alcance da relação.

$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “Nome” e lista os nomes “Maria”, “Arm and o”, “Cynthia”, “Kelly” e “Rachel”. A tabela à direita tem o cabeçalho “Aniversário” e lista as datas “18 de janeiro”, “15 de março”, “6 de novembro” e “8 de dezembro”. Há uma seta para cada nome na tabela de nomes que começa com o nome e aponta para uma data na tabela de aniversários. A primeira flecha vai de Maria até 6 de novembro. A segunda flecha vai de Arm and Go até 18 de janeiro. A terceira flecha vai de Cynthia até 8 de dezembro. A quarta flecha vai de Kelly até 15 de março. A quinta flecha vai de Rachel até 6 de novembro.$

Responda

ⓐ (Maria, 6 de novembro), (Arm and o, 18 de janeiro), (Cynthia, 8 de dezembro), (Kelly, 15 de março), (Rachel, 6 de novembro)

ⓑ {Maria, Arm e eu, Cynthia, Kelly, Rachel}

Um gráfico é outra forma pela qual uma relação pode ser representada. O conjunto de pares ordenados de todos os pontos traçados é a relação. O conjunto de todas as coordenadas x é o domínio da relação e o conjunto de todas as coordenadas y é o intervalo. Geralmente, escrevemos os números em ordem crescente para o domínio e o intervalo.

Exemplo$\PageIndex{7}$

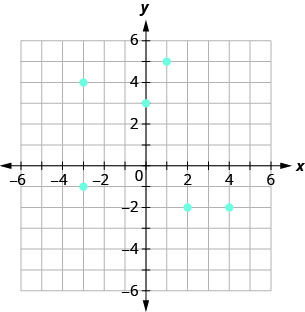
Use o gráfico da relação com

listar os pares ordenados da relação
encontre o domínio da relação
encontre o alcance da relação.

$A figura mostra o gráfico de alguns pontos no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. Os pontos (menos 3, 4), (menos 3, menos 1), (0, 3), (1, 5), (2, menos 2) e (4, menos 2).$

Responda

ⓐ Os pares ordenados da relação são:\[{\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber\]

ⓑ O domínio é o conjunto de todos os valores x da relação:$\quad {\{−3,0,1,2,4}\}$.

Observe que, enquanto$−3$ se repete, ele só é listado uma vez.

Observe que, enquanto$−2$ se repete, ele só é listado uma vez.

Exemplo$\PageIndex{8}$

Use o gráfico da relação com

listar os pares ordenados da relação
encontre o domínio da relação
encontre o alcance da relação.
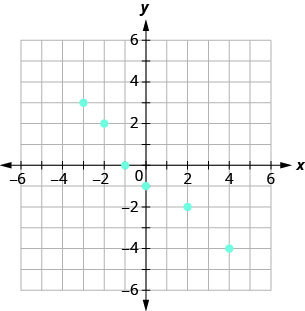
$A figura mostra o gráfico de alguns pontos no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. Os pontos (menos 3, 3), (menos 2, 2), (menos 1, 0), (0, menos 1), (2, menos 2) e (4, menos 4).$

Responda: ⓐ$(−3,3),(−2,2),(−1,0),$
$(0,−1),(2,−2),(4,−4)$
ⓑ${\{−3,−2,−1,0,2,4}\}$
ⓒ${\{3,2,0,−1,−2,−4}\}$

Exemplo$\PageIndex{9}$

Use o gráfico da relação com

listar os pares ordenados da relação
encontre o domínio da relação
encontre o alcance da relação.

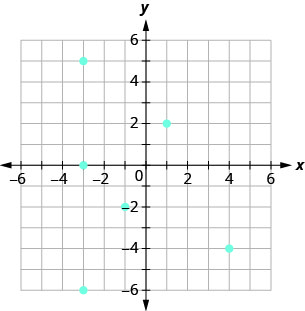
$A figura mostra o gráfico de alguns pontos no plano da coordenada x y. Os eixos x e y vão de menos 6 a 6. Os pontos (menos 3, 5), (menos 3, 0), (menos 3, menos 6), (menos 1, menos 2), (1, 2) e (4, menos 4).$

Responda: ⓐ$(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ${\{−3,−1,1,4}\}$
ⓒ${\{−6,0,5,−2,2,−4}\}$

Determine se uma relação é uma função

Um tipo especial de relação, chamado de função, ocorre extensivamente em matemática. Uma função é uma relação que atribui a cada elemento em seu domínio exatamente um elemento no intervalo. Para cada par ordenado na relação, cada valor x é combinado com apenas um valor y.

Definição: Função

Uma função é uma relação que atribui a cada elemento em seu domínio exatamente um elemento no intervalo.

O exemplo de aniversário do Example nos ajuda a entender essa definição. Toda pessoa faz aniversário, mas ninguém tem dois aniversários. É normal que duas pessoas façam aniversário. ^{Tudo bem que Danny e Stephen compartilhem 24 de ^julho como aniversário e que June e Liz compartilhem 2 de agosto.} Como cada pessoa tem exatamente um aniversário, a relação no Exemplo é uma função.

A relação mostrada pelo gráfico em Exemplo inclui os pares ordenados$(−3,−1)$$(−3,4)$ e. Isso está bem em uma função? Não, pois é como se uma pessoa tivesse dois aniversários diferentes.

Exemplo$\PageIndex{10}$

Use o conjunto de pares ordenados para (i) determinar se a relação é uma função (ii) encontre o domínio da relação (iii) encontre o intervalo da relação.

${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

Responda

ⓐ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) Cada valor x é combinado com apenas um valor y. Então, essa relação é uma função.

(ii) O domínio é o conjunto de todos os valores x na relação.
O domínio é:${\{−3,−2,−1,0,1,2,3}\}$.

(iii) O intervalo é o conjunto de todos os valores y na relação. Observe que não listamos valores de intervalo duas vezes.
O alcance é:${\{27,8,1,0}\}$.

ⓑ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) O valor x 9 é combinado com dois valores y, ambos 3$−3$ e. Portanto, essa relação não é uma função.

(ii) O domínio é o conjunto de todos os valores x na relação. Observe que não listamos valores de domínio duas vezes.
O domínio é:${\{0,1,2,4,9}\}$.

(iii) O intervalo é o conjunto de todos os valores y na relação.
O alcance é:${\{−3,−2,−1,0,1,2,3}\}$.

Exemplo$\PageIndex{11}$

Use o conjunto de pares ordenados para (i) determinar se a relação é uma função (ii) encontre o domínio da relação (iii) encontre o intervalo da função.

${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

Responda: ⓐ Sim;${\{−3,−2,−1,0,1,2,3}\}$;
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ Não;${\{0,2,4,8}\}$;
${\{−4,−2,−1,0,1,2,4}\}$

Exemplo$\PageIndex{12}$

Use o conjunto de pares ordenados para (i) determinar se a relação é uma função (ii) encontre o domínio da relação (iii) encontre o intervalo da relação.

${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

Responda: ⓐ Não${\{0,1,8,27}\}$;
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ Sim;${\{7,−5,8,0,−6,−2,−1}\}$;
${\{−3,−4,0,4,2,3}\}$

Exemplo$\PageIndex{13}$

Use o mapeamento para

determinar se a relação é uma função
encontre o domínio da relação
encontre o alcance da relação.

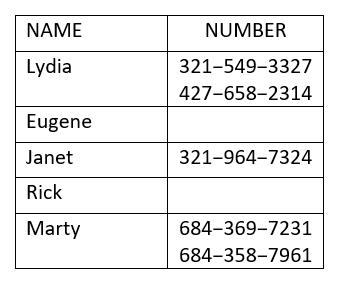
$clipboard_e358fef1793647353f09157074f4029e0.png$

Responda

ⓐ Tanto Lydia quanto Marty têm dois números de telefone. Portanto, cada valor x não é combinado com apenas um valor y. Portanto, essa relação não é uma função.

ⓑ O domínio é o conjunto de todos os valores x na relação. O domínio é: {Lydia, Eugene, Janet, Rick, Marty}

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

Exemplo$\PageIndex{14}$

Use o mapeamento para ⓐ determinar se a relação é uma função ⓑ encontre o domínio da relação ⓒ encontre o alcance da relação.

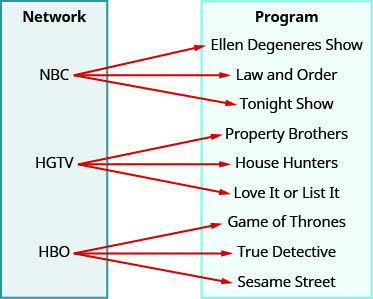
$Esta figura mostra duas tabelas, cada uma com uma coluna. A tabela à esquerda tem o cabeçalho “Rede” e lista as estações de televisão “NBC”, “HGTV” e “HBO”. A tabela à direita tem o cabeçalho “Programa” e lista os programas de televisão “Ellen Degeneres Show”, “Law and Order”, “Tonight Show”, “Property Brothers”, “House Hunters”, “Love it or List it”, “Game of Thrones”, “True Detective” e “Vila Sésamo”. Há setas que começam em uma rede na primeira tabela e apontam para um programa na segunda tabela. A primeira flecha vai da NBC para o Ellen Degeneres Show. A segunda flecha vai da NBC para Law and Order. A terceira flecha vai da NBC para o Tonight Show. A quarta seta vai da HGTV para a Property Brothers. A quinta flecha vai da HGTV para House Hunters. A sexta seta vai da HGTV para Amar ou Listar. A sétima flecha vai da HBO para Game of Thrones. A oitava flecha vai da HBO para True Detective. A nona flecha vai da HBO para a Vila Sésamo.$

Responda: ⓐ não ⓑ {NBC, HGTV, HBO} ⓒ {Ellen Degeneres Show, Law and Order, Tonight Show, Property Brothers, House Hunters, Ame ou liste, Game of Thrones, True Detective, Vila Sésamo}

Exemplo$\PageIndex{15}$

Use o mapeamento para

determinar se a relação é uma função
encontre o domínio da relação
encontre o alcance da relação.

Responda: ⓐ Não ⓑ {Neal, Krystal, Kelvin, George, Christa, Mike} ⓒ {trabalho 123-567-4839, 231-378-5941 célula, 743-469-9731 célula, 567-534-2970 trabalho, 684-369-7231 célula, 798-367-8541 célula, 639-847-6971 célula}

Em álgebra, na maioria das vezes, as funções serão representadas por uma equação. É mais fácil ver se a equação é uma função quando ela é resolvida para y. Se cada valor de x resultar em apenas um valor de y, a equação definirá uma função.

Exemplo$\PageIndex{16}$

Determine se cada equação é uma função.

$2x+y=7$
$y=x^2+1$
$x+y^2=3$

Responda

ⓐ$2x+y=7$

Para cada valor de x, nós o multiplicamos por$−2$ e, em seguida, adicionamos 7 para obter o valor y.

	$.$
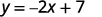
Por exemplo, se$x=3$:	$.$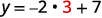
	$.$

Temos isso quando$x=3$, então$y=1$. Funcionaria de forma semelhante para qualquer valor de x. Como cada valor de x corresponde a apenas um valor de y, a equação define uma função.

ⓑ$y=x^2+1$

Para cada valor de x, nós o elevamos ao quadrado e, em seguida, adicionamos 1 para obter o valor y.

	$.$
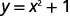
Por exemplo, se$x=2$:	$.$
	$.$

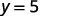
Temos isso quando$x=2$, então$y=5$. Funcionaria de forma semelhante para qualquer valor de x. Como cada valor de x corresponde a apenas um valor de y, a equação define uma função.

ⓒ

	$.$
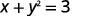
Isole o termo y.	$.$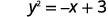
Vamos substituir$x=2$.	$.$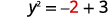
	$.$
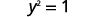
Isso nos dá dois valores para y.	$y=1\space y=−1$

Mostramos que quando$x=2$, então$y=1$$y=−1$ e. Funcionaria de forma semelhante para qualquer valor de x. Como cada valor de x não corresponde a apenas um valor de y, a equação não define uma função.

Exemplo$\PageIndex{17}$

Determine se cada equação é uma função.

$4x+y=−3$
$x+y^2=1$
$y−x^2=2$

Responda: ⓐ sim ⓑ não ⓒ sim

Exemplo$\PageIndex{18}$

Determine se cada equação é uma função.

$x+y^2=4$
$y=x^2−7$
$y=5x−4$

Responda: ⓐ não ⓑ sim ⓒ sim

Encontre o valor de uma função

É muito conveniente nomear uma função e, na maioria das vezes, chamamos ela de f, g, h, F, G ou H. Em qualquer função, para cada valor x do domínio, obtemos um valor y correspondente no intervalo. Para a função$f$, escrevemos esse valor de intervalo$y$ como$f(x)$. Isso é chamado de notação de função e é lido$f$ de$x$ ou o valor de$f$ at$x$. Nesse caso, os parênteses não indicam multiplicação.

Definição: Notação de função

Para a função$y=f(x)$

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

Lemos a$f(x)$ partir$f$ de$x$ ou o valor de$f$ at$x$.

Chamamos x de variável independente, pois ela pode ser qualquer valor no domínio. Chamamos y de variável dependente, pois seu valor depende de x.

VARIÁVEIS INDEPENDENTES E DEPENDENTES

Para a função$y=f(x)$,

\[\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}\]

Assim como quando você encontrou a variável x pela primeira vez, a notação da função pode ser bastante inquietante. Parece estranho porque é novo. Você se sentirá mais confortável com a notação ao usá-la.

Vamos dar uma olhada na equação$y=4x−5$. Para encontrar o valor de y quando$x=2$, sabemos que devemos substituir$x=2$ a equação e depois simplificar.

	$.$
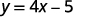Seja x = 2.	$.$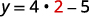
	$.$

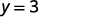O valor da função at$x=2$ é 3.

Fazemos a mesma coisa usando a notação de função, a equação$y=4x−5$ pode ser escrita como$f(x)=4x−5$. Para encontrar o valor quando$x=2$, escrevemos:

	$.$
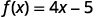Seja x = 2.	$.$
	$.$

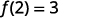O valor da função at$x=2$ é 3.

Esse processo de encontrar o valor de$f(x)$ para um determinado valor de x é chamado de avaliação da função.

Exemplo$\PageIndex{19}$

Para a função$f(x)=2x^2+3x−1$, avalie a função.

$f(3)$
$f(−2)$
$f(a)$

Responda

ⓐ

	$.$
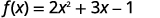
Para avaliar$f(3)$, substitua 3 por x.	$.$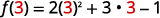
Simplifique.	$.$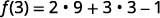
	$.$
	$.$

ⓑ

		$.$
$.$		$.$
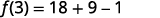
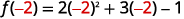
Simplifique.		$.$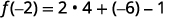
		$.$
		$.$

ⓒ

	$.$
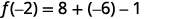
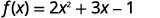
Para avaliar f (a), f (a), substitua a por x.	$.$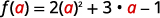
Simplifique.	$.$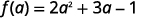

Exemplo$\PageIndex{20}$

Para a função$f(x)=3x^2−2x+1$, avalie a função.

$f(3)$
$f(−1)$
$f(t)$

Exemplo$\PageIndex{21}$

Para a função$f(x)=2x^2+4x−3$, avalie a função.

$f(2)$
$f(−3)$
$f(h)$

No último exemplo, encontramos$f(x)$ um valor constante de x. No próximo exemplo, somos solicitados a encontrar$g(x)$ com valores de x que são variáveis. Ainda seguimos o mesmo procedimento e substituímos as variáveis pelo x.

Exemplo$\PageIndex{22}$

Para a função$g(x)=3x−5$, avalie a função.

$g(h^2)$
$g(x+2)$
$g(x)+g(2)$

Responda

ⓐ

			$.$
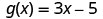
Para avaliar$g(h^2)$, substitua$h^2$ por x.			$.$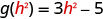
			$.$

ⓑ

	$.$
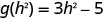
Para avaliar$g(x+2)$, substitua$x+2$ por x.	$.$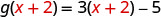
Simplifique.	$.$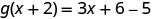
	$.$

ⓒ

		$.$
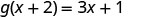
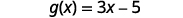
Para avaliar$g(x)+g(2)$, primeiro encontre$g(2)$.		$.$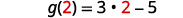
		$.$
$.$		$.$
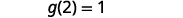
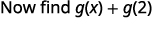
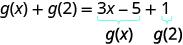
Simplifique.		$.$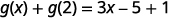
		$.$

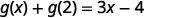
Observe a diferença entre a parte ⓑ e a ⓒ. Nós recebemos$g(x+2)=3x+1$$g(x)+g(2)=3x−4$ e. Então, vemos isso$g(x+2)\neq g(x)+g(2)$.

Exemplo$\PageIndex{23}$

Para a função$g(x)=4x−7$, avalie a função.

$g(m^2)$
$g(x−3)$
$g(x)−g(3)$

Exemplo$\PageIndex{24}$

Para a função$h(x)=2x+1$, avalie a função.

$h(k^2)$
$h(x+1)$
$h(x)+h(1)$

Muitas situações cotidianas podem ser modeladas usando funções.

Exemplo$\PageIndex{25}$

O número de e-mails não lidos na conta de Sylvia é 75. Esse número cresce em 10 e-mails não lidos por dia. A função$N(t)=75+10t$ representa a relação entre o número de e-mails, N, e o tempo, t, medido em dias.

Determine a variável independente e dependente.
Encontre$N(5)$. Explique o que esse resultado significa.

Responda

ⓐ O número de e-mails não lidos é uma função do número de dias. O número de e-mails não lidos, N, depende do número de dias, t. Portanto, a variável N é a variável dependente e a variável tt é a variável independente.

ⓑ Encontre$N(5)$. Explique o que esse resultado significa.

	$.$
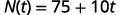
Substitua em t=5.t=5.	$.$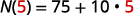
Simplifique.	$.$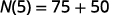
	$.$

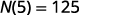
Como 5 é o número de dias,$N(5)$, é o número de e-mails não lidos após 5 dias. Após 5 dias, há 125 e-mails não lidos na conta.

Exemplo$\PageIndex{26}$

O número de e-mails não lidos na conta de Bryan é 100. Esse número cresce em 15 e-mails não lidos por dia. A função$N(t)=100+15t$ representa a relação entre o número de e-mails, N, e o tempo, t, medido em dias.

Determine a variável independente e dependente.
Encontre$N(7)]$. Explique o que esse resultado significa.

Responda: ⓐ t IND; N DEP ⓑ 205; o número de e-mails não lidos na conta de Bryan no sétimo dia.

Exemplo$\PageIndex{27}$

O número de e-mails não lidos na conta de Anthony é 110. Esse número cresce em 25 e-mails não lidos por dia. A função$N(t)=110+25t$ representa a relação entre o número de e-mails, N, e o tempo, t, medido em dias.

Determine a variável independente e dependente.
Encontre$N(14)$. Explique o que esse resultado significa.

Responda: ⓐ t IND; N DEP ⓑ 460; o número de e-mails não lidos na conta de Anthony no décimo quarto dia

Acesse este recurso on-line para obter instruções e práticas adicionais sobre relações e funções.

Introdução às funções

Conceitos-chave

Notação da função: Para a função$y=f(x)$
- f é o nome da função
- x é o valor do domínio
- $f(x)$é o valor do intervalo y correspondente ao valor x
  Lemos$f(x)$ como f de x ou o valor de f em x.
Variáveis independentes e dependentes: Para a função$y=f(x)$,
- x é a variável independente, pois pode ser qualquer valor no domínio
- y é a variável dependente, pois seu valor depende de x

Glossário

domínio de uma relação: O domínio de uma relação são todos os valores de x nos pares ordenados da relação.

função: Uma função é uma relação que atribui a cada elemento em seu domínio exatamente um elemento no intervalo.

mapeamento: Às vezes, um mapeamento é usado para mostrar uma relação. As setas mostram o emparelhamento dos elementos do domínio com os elementos do intervalo.

alcance de uma relação: O intervalo de uma relação são todos os valores de y nos pares ordenados da relação.

relação: Uma relação é qualquer conjunto de pares ordenados, (x, y). (x, y). Todos os valores x nos pares ordenados juntos formam o domínio. Todos os valores de y nos pares ordenados juntos formam o intervalo.

Definição: Relação

Exemplo\(\PageIndex{1}\)

Exemplo\(\PageIndex{2}\)

Exemplo\(\PageIndex{3}\)

MAPEAMENTO

Exemplo\(\PageIndex{4}\)

Exemplo\(\PageIndex{5}\)

Exemplo\(\PageIndex{6}\)

Exemplo\(\PageIndex{7}\)

Exemplo\(\PageIndex{8}\)

Exemplo\(\PageIndex{9}\)

Definição: Função

Exemplo\(\PageIndex{10}\)

Exemplo\(\PageIndex{11}\)

Exemplo\(\PageIndex{12}\)

Exemplo\(\PageIndex{13}\)

Exemplo\(\PageIndex{14}\)

Exemplo\(\PageIndex{15}\)

Exemplo\(\PageIndex{16}\)

Exemplo\(\PageIndex{17}\)

Exemplo\(\PageIndex{18}\)

Definição: Notação de função

VARIÁVEIS INDEPENDENTES E DEPENDENTES

Exemplo\(\PageIndex{19}\)

Exemplo\(\PageIndex{20}\)

Exemplo\(\PageIndex{21}\)

Exemplo\(\PageIndex{22}\)

Exemplo\(\PageIndex{23}\)

Exemplo\(\PageIndex{24}\)

Exemplo\(\PageIndex{25}\)

Exemplo\(\PageIndex{26}\)

Exemplo\(\PageIndex{27}\)

	$.$
Isole o termo y.	$.$
Vamos substituir\(x=2\).	$.$
	$.$
Isso nos dá dois valores para y.	\(y=1\space y=−1\)

	$.$
Para avaliar\(f(3)\), substitua 3 por x.	$.$
Simplifique.	$.$
	$.$
	$.$

	$.$
Para avaliar\(g(x+2)\), substitua\(x+2\) por x.	$.$
Simplifique.	$.$
	$.$

		$.$
Para avaliar\(g(x)+g(2)\), primeiro encontre\(g(2)\).		$.$
		$.$
$.$		$.$
Simplifique.		$.$
		$.$