13.3 : Gravitation près de la surface de la Terre
- Page ID
- 191313
- Expliquer le lien entre les constantes G et g
- Déterminer la masse d'un corps astronomique à partir de l'accélération en chute libre à sa surface
- Décrire comment la valeur de g varie en fonction de l'emplacement et de la rotation de la Terre
Dans cette section, nous observons comment la loi de la gravitation de Newton s'applique à la surface d'une planète et comment elle est liée à ce que nous avons appris précédemment sur la chute libre. Nous examinons également les effets gravitationnels au sein des corps sphériques.
Poids
Rappelons que l'accélération d'un objet en chute libre près de la surface de la Terre est d'environ g = 9,80 m/s 2. La force à l'origine de cette accélération s'appelle le poids de l'objet et, selon la deuxième loi de Newton, elle a la valeur mg. Ce poids est présent que l'objet soit en chute libre ou non. Nous savons maintenant que cette force est la force gravitationnelle entre l'objet et la Terre. Si nous substituons mg à la magnitude de\(\vec{F}_{12}\) dans la loi de Newton de la gravitation universelle, m pour m 1 et M E pour m 2, nous obtenons l'équation scalaire
\[mg = G \frac{m M_{E}}{r^{2}} \label{13.1}\]
où r est la distance entre les centres de masse de l'objet et la Terre. Le rayon moyen de la Terre est d'environ 6370 km. Ainsi, pour les objets situés à quelques kilomètres de la surface de la Terre, nous pouvons prendre\(r = R_E\) (Figure\(\PageIndex{1}\)). La masse m de l'objet s'annule, laissant
\[g = G \frac{M_{E}}{r^{2}} \ldotp \label{13.2}\]
Cela explique pourquoi toutes les masses tombent librement avec la même accélération. Nous avons ignoré le fait que la Terre accélère également vers l'objet qui tombe, mais cela est acceptable tant que la masse de la Terre est beaucoup plus grande que celle de l'objet.
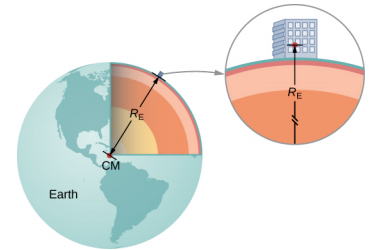
Vous êtes-vous déjà demandé comment nous connaissions la masse de la Terre ? Nous ne pouvons certainement pas le placer sur une balance. Les valeurs de g et du rayon de la Terre ont été mesurées avec une précision raisonnable il y a des siècles.
- Utilisez les valeurs standard de g, R E et de l'équation \ ref {13.2} pour déterminer la masse de la Terre.
- Estimez la valeur de g sur la Lune. Prenez le fait que la Lune a un rayon d'environ 1 700 km (une valeur de cette précision a été déterminée il y a plusieurs siècles) et supposez qu'elle a la même densité moyenne que la Terre, soit 5 500 kg/m 3.
Stratégie
Avec les valeurs connues de g et R E, nous pouvons utiliser l'équation \ ref {13.2} pour trouver M E. Pour la Lune, nous utilisons l'hypothèse d'une densité moyenne égale pour déterminer la masse à partir d'un rapport entre les volumes de la Terre et de la Lune.
Solution
- En réorganisant l'équation \ ref {13.2}, nous avons $$M_ {E} = \ frac {g R_ {E} ^ {2}} {G} = \ frac {(9,80 \ ; m/s^ {2}) (6,37 \ fois 10^ {6} \ ; m) ^ {2}} {6,67 \ times 10^ {-11} \ ; N \ ; \ cdotp ^ {2} /kg^ {2}} = 5,95 \ fois 10^ {24} \ ; kg \ ldotp$$
- Le volume d'une sphère est proportionnel au rayon cubique, donc un ratio simple nous donne $$ \ frac {M_ {M}} {M_ {E}} = \ frac {R_ {M} ^ {3}} {R_ {E} ^ {3}} \ flèche droite M_ {M} = \ left (\ dfrac {(1,7 \ times 10^ {6}} \ ; m) ^ {3}} {(6,37 \ fois 10^ {6} \ ; m) ^ {3}} \ right) (5,95 \ fois 10^ {24} \ ; kg) = 1,1 \ fois 10^ {23} \ ; kg \ LDotp$$Nous utilisons maintenant Équation \ ref {13.2}. $$g_ {M} = G \ frac {M_ {M}} {r_ {M} ^ {2}} = (6,67 \ fois 10 ^ {-11} \ ; N \ ; \ cdotp m^ {2} /kg^ {2}) \ left (\ dfrac {1,1 \ fois 10 ^ {23}} \ ; kg} {(1,7 \ fois 10 ^ {6} \ ; m) ^ {2}} \ droite) = 2,5 \ ; m/s^ {2} $$
L'importance
Dès que Cavendish a déterminé la valeur de G en 1798, la masse de la Terre a pu être calculée. (En fait, c'était le but ultime de l'expérience de Cavendish au départ.) La valeur que nous avons calculée pour g de la Lune est incorrecte. La densité moyenne de la Lune n'est en fait que de 3340 kg/m 3 et g = 1,6 m/s 2 à la surface. Newton a tenté de mesurer la masse de la Lune en comparant l'effet du Soleil sur les marées océaniques de la Terre à celui de la Lune. Sa valeur était un facteur deux trop faible. Les valeurs les plus précises pour g et la masse de la Lune proviennent du suivi du mouvement des vaisseaux spatiaux qui ont orbité autour de la Lune. Mais la masse de la Lune peut en fait être déterminée avec précision sans aller sur la Lune. La Terre et la Lune orbitent autour d'un centre de gravité commun, et des mesures astronomiques minutieuses peuvent déterminer cet emplacement. Le rapport entre la masse de la Lune et celle de la Terre est le rapport entre [la distance entre le centre de masse commun et le centre de la Lune] et [la distance entre le centre de masse commun et le centre de la Terre].
Plus loin dans cette section, nous verrons que la masse d'autres corps astronomiques peut également être déterminée par la période pendant laquelle les petits satellites gravitent autour d'eux. Mais jusqu'à ce que Cavendish détermine la valeur de G, les masses de tous ces corps étaient inconnues.
Quelle est la valeur de g 400 km au-dessus de la surface de la Terre, là où se trouve la Station spatiale internationale ?
Solution
En utilisant la valeur de M E et en notant que le rayon est r = R E + 400 km, nous utilisons l'équation \ ref {13.2} pour trouver g. À partir de l'équation \ ref {13.2}, nous avons
\[g = G \frac{M_{E}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \left(\dfrac{5.96 \times 10^{24}\; kg}{(6.37 \times 10^{6} + 400 \times 10^{3}\; m)^{2}}\right) = 8.67\; m/s^{2} \ldotp\]
L'importance
Nous voyons souvent des vidéos d'astronautes dans des stations spatiales, apparemment en apesanteur. Mais il est clair que la force de gravité agit sur eux. En comparant la valeur de g que nous venons de calculer à celle de la Terre (9,80 m/s 2), nous constatons que les astronautes de la Station spatiale internationale ont encore 88 % de leur poids. Ils semblent être en apesanteur uniquement parce qu'ils sont en chute libre. Nous y reviendrons dans la section Orbites satellites et énergie.
Quel est votre poids au sommet d'un grand immeuble par rapport à celui du premier étage ? Pensez-vous que les ingénieurs doivent prendre en compte l'évolution de la valeur de g lors de la conception du support structurel d'un bâtiment de très grande hauteur ?
Le champ gravitationnel
L'équation \ ref {13.2} est une équation scalaire qui donne l'amplitude de l'accélération gravitationnelle en fonction de la distance par rapport au centre de la masse qui provoque l'accélération. Mais nous aurions pu conserver la forme vectorielle de la force de gravité dans l'équation \ ref {13.1}, et écrire l'accélération sous forme vectorielle comme
\[\vec{g} = G \frac{M}{r^{2}} \hat{r} \ldotp\]
Nous identifions le champ vectoriel représenté par\(\vec{g}\) comme étant le champ gravitationnel provoqué par la masse M. Nous pouvons imaginer le champ comme indiqué sur la figure\(\PageIndex{2}\). Les lignes sont dirigées radialement vers l'intérieur et sont réparties symétriquement autour de la masse.
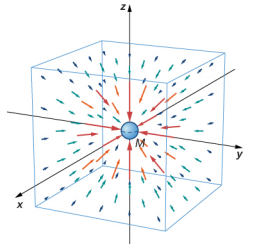
Comme pour tout champ vectoriel, la direction de\(\vec{g}\) est parallèle aux lignes de champ en tout point. La force de\(\vec{g}\) en tout point est inversement proportionnelle à l'espacement des lignes. Une autre façon de le dire est que l'amplitude du champ dans n'importe quelle région est proportionnelle au nombre de lignes qui traversent une unité de surface, soit en fait une densité de lignes. Comme les lignes sont régulièrement espacées dans toutes les directions, le nombre de lignes par unité de surface à une distance r de la masse est le nombre total de lignes divisé par la surface d'une sphère de rayon r, qui est proportionnelle à r 2. Cette image représente donc parfaitement la loi des carrés inverses, en plus d'indiquer la direction du champ. Dans l'image de terrain, nous disons qu'une masse m interagit avec le champ gravitationnel de la masse M. Nous utiliserons le concept de champs de manière très avantageuse dans les sections suivantes sur l'électromagnétisme.
Poids apparent : prise en compte de la rotation de la Terre
Comme nous l'avons vu dans Applications des lois de Newton, les objets se déplaçant à vitesse constante dans un cercle ont une accélération centripète dirigée vers le centre du cercle, ce qui signifie qu'il doit y avoir une force nette dirigée vers le centre de ce cercle. Comme tous les objets à la surface de la Terre se déplacent dans un cercle toutes les 24 heures, il doit y avoir une force centripète nette sur chaque objet dirigée vers le centre de ce cercle.
Considérons d'abord un objet de masse m situé à l'équateur, suspendu à une échelle (Figure\(\PageIndex{3}\)). L'échelle exerce une force ascendante\(\vec{F}_{s}\) s'éloignant du centre de la Terre. Il s'agit de la lecture sur la balance, et donc du poids apparent de l'objet. Le poids (mg) pointe vers le centre de la Terre. Si la Terre ne tournait pas, l'accélération serait nulle et, par conséquent, la force nette serait nulle, soit F s = mg. Ce serait la véritable lecture du poids.
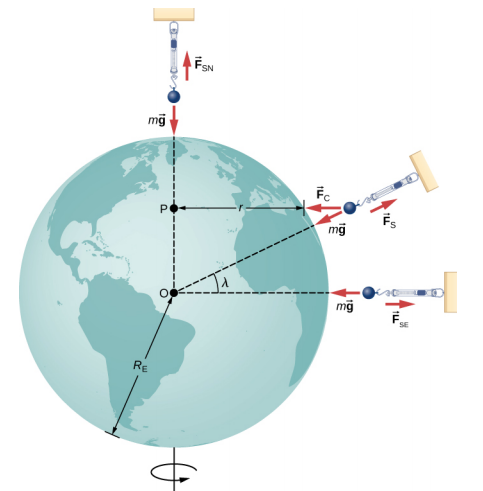
Avec la rotation, la somme de ces forces doit fournir l'accélération centripète,\(a_c\). En utilisant la deuxième loi de Newton, nous avons
\[\sum F = F_{s} - mg = ma_{c} \quad where\; a_{c} = - \frac{v^{2}}{r} \ldotp \label{13.3}\]
Notez que a c pointe dans la même direction que le poids ; il est donc négatif. La vitesse tangentielle v est la vitesse à l'équateur et r est R E. Nous pouvons calculer la vitesse simplement en constatant que les objets situés sur l'équateur parcourent la circonférence de la Terre en 24 heures. Utilisons plutôt l'expression alternative pour un c dans Motion in Two and Three Dimensions. Rappelons que la vitesse tangentielle est liée à la vitesse angulaire (\(\omega\)) par v =\(\omega\) r. Nous avons donc un c = −r\(\omega\) 2. En réorganisant l'équation 13.3 et en y substituant r = R E, le poids apparent à l'équateur est
\[F_{s} = m (g - R_{E} \omega^{2}) \ldotp\]
La vitesse angulaire de la Terre est partout
\[\omega = \frac{2 \pi\; rad}{24\; hr \times 3600\; s/hr} = 7.27 \times 10^{-5}\; rad/s \ldotp\]
En remplaçant les valeurs de R E et\(\omega\), nous avons R E\(\omega\) 2 = 0,0337 m/s 2. Cela ne représente que 0,34 % de la valeur de la gravité, il s'agit donc clairement d'une petite correction.
À quelle vitesse la Terre aurait-elle besoin de tourner pour que ceux qui se trouvent à l'équateur aient un poids apparent nul ? Quelle serait la durée de la journée ?
Stratégie
À l'aide de l'équation \ ref {13.3}, nous pouvons mettre le poids apparent (F s) à zéro et déterminer l'accélération centripète requise. À partir de là, nous pouvons trouver la vitesse à l'équateur. La durée de la journée est le temps requis pour une rotation complète.
Solution
À partir de l'équation \ ref {13.2}, nous avons\(\sum\) F = F s − mg = ma c, donc en réglant F s = 0, nous obtenons g = a c. En utilisant l'expression pour un c, en remplaçant le rayon de la Terre et la valeur standard de la gravité, nous obtenons
\[\begin{split} a_{c} & = \frac{v^{2}}{r} = g \\ v & = \sqrt{gr} = \sqrt{(9.80\; m/s^{2})(6.37 \times 10^{6}\; m)} = 7.91 \times 10^{3}\; m/s \ldotp \end{split}\]
La période T est la durée d'une rotation complète. Par conséquent, la vitesse tangentielle est la circonférence divisée par T, donc nous avons
\[\begin{split} v & = \frac{2 \pi r}{T} \\ T & = \frac{2 \pi r}{v} = \frac{2 \pi (6.37 \times 10^{6}\; m)}{7.91 \times 10^{3}\; m/s} = 5.06 \times 10^{3}\; s \ldotp \end{split}\]
Cela représente environ 84 minutes.
L'importance
Nous verrons plus loin dans cette section que cette vitesse et cette durée du jour correspondraient également à la vitesse orbitale et à la période d'un satellite en orbite à la surface de la Terre. Bien qu'une telle orbite ne soit pas possible près de la surface de la Terre en raison de la résistance de l'air, elle n'est certainement possible qu'à quelques centaines de kilomètres au-dessus de la Terre.
Résultats loin de l'équateur
Aux pôles, a c → 0 et Fs = mg, comme c'est le cas sans rotation. À toute autre latitude\(\lambda\), la situation est plus complexe. L'accélération centripète est dirigée vers le point P de la figure et le rayon devient\(r = R_E \cos \lambda\). La somme vectorielle du poids et\(\vec{F}_{s}\) doit pointer vers le point P, donc\(\vec{F}_{s}\) ne pointe plus loin du centre de la Terre. (La différence est faible et exagérée sur la figure.) Un fil à plomb pointera toujours dans cette direction déviée. Tous les bâtiments sont construits alignés le long de cette direction déviée, et non le long d'un rayon passant par le centre de la Terre. Pour les bâtiments les plus hauts, cela représente une déviation de quelques mètres au sommet.
Il convient également de noter que la Terre n'est pas une sphère parfaite. L'intérieur est partiellement liquide, ce qui accentue le gonflement de la Terre à l'équateur en raison de sa rotation. Le rayon de la Terre est environ 30 km plus grand à l'équateur qu'aux pôles. Il s'agit d'un exercice consistant à comparer la force de gravité aux pôles à celle de l'équateur à l'aide de l'équation \ ref {13.2}. La différence est comparable à la différence due à la rotation et va dans le même sens. Apparemment, vous pouvez vraiment perdre du « poids » en vous installant sous les tropiques.
La gravité loin de la surface
Plus tôt, nous avons déclaré sans preuve que la loi de la gravitation s'applique aux objets sphériquement symétriques, où la masse de chaque corps agit comme si elle se trouvait au centre du corps. Puisque l'équation \ ref {13.2} est dérivée de l'équation \ ref {13.1}, elle est également valide pour les distributions de masse symétriques, mais les deux équations ne sont valables que pour les valeurs de\(r ≥ R_E\). Comme nous l'avons vu dans l'exemple 13.4, à 400 km au-dessus de la surface de la Terre, là où tourne la Station spatiale internationale, la valeur de\(g\) est de 8,67 m/s 2. (Nous verrons plus loin qu'il s'agit également de l'accélération centripète de l'ISS.)
Pour\(r < R_E\), l'équation \ ref {13.1} et l'équation \ ref {13.2} ne sont pas valides. Cependant, nous pouvons déterminer g pour ces cas en utilisant un principe issu de la loi de Gauss, qui est un puissant outil mathématique que nous étudierons plus en détail plus loin dans le cours. Une conséquence de la loi de Gauss, appliquée à la gravitation, est que seule la masse contenue dans r contribue à la force gravitationnelle. De plus, cette masse, comme auparavant, peut être considérée comme étant située au centre. L'effet gravitationnel de la masse en dehors de r n'a aucun effet net.
Deux cas particuliers très intéressants se présentent. Pour une planète sphérique à densité constante, la masse comprise dans r est la densité multipliée par le volume dans r. Cette masse peut être considérée comme étant située au centre. En remplaçant M E par la seule masse comprise dans r, M =\(\rho\) x (volume d'une sphère) et R E par r, l'équation \ ref {13.2} devient
\[g = G \frac{M_{E}}{R_{E}^{2}} = G \frac{\rho \left(\dfrac{4}{3} \pi r^{3}\right)}{r^{2}} = \frac{4}{3} G \rho \pi r \ldotp\]
La valeur de g, et donc votre poids, diminue linéairement lorsque vous descendez un trou jusqu'au centre de la planète sphérique. Au centre, vous êtes en apesanteur, car la masse de la planète tire de la même manière dans toutes les directions. En fait, la densité de la Terre n'est pas constante et la Terre n'est pas solide partout. La figure\(\PageIndex{4}\) montre le profil selon lequel\(g\) la Terre avait une densité constante et le profil le plus probable basé sur des estimations de densité dérivées de données sismiques.
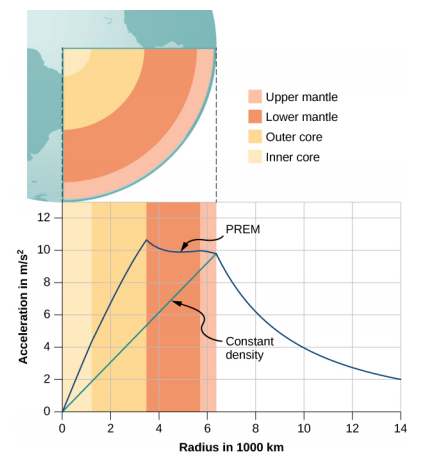
Le deuxième cas intéressant concerne la vie sur une planète à coquille sphérique. Ce scénario a été proposé dans de nombreux récits de science-fiction. Sans tenir compte des problèmes techniques importants, la coque pourrait être construite avec le rayon et la masse totale souhaités, de telle sorte que g à la surface soit le même que celui de la Terre. Pouvez-vous deviner ce qui se passe une fois que vous descendez en ascenseur jusqu'à l'intérieur de la coque, où il n'y a aucune masse entre vous et le centre ? Quels avantages cela apporterait-il pour parcourir de grandes distances d'un point de la sphère à un autre ? Et enfin, quel effet aurait-il si la planète tournait ?


