13.2 : La loi de Newton sur la gravitation universelle
- Page ID
- 191314
- Énumérez les étapes importantes de l'histoire de la gravitation
- Calculez la force gravitationnelle entre deux masses ponctuelles
- Estimer la force gravitationnelle entre des collections de masse
Nous passons d'abord en revue l'histoire de l'étude de la gravitation, en mettant l'accent sur les phénomènes qui, depuis des milliers d'années, ont incité les philosophes et les scientifiques à chercher une explication. Nous examinons ensuite la forme la plus simple de la loi de Newton sur la gravitation universelle et comment l'appliquer.
L'histoire de la gravitation
Les premiers philosophes se demandaient pourquoi les objets avaient naturellement tendance à tomber vers le sol. Aristote (384—322 av. J.-C.) croyait que c'était la nature des roches de rechercher la Terre et la nature du feu de rechercher les cieux. Brahmagupta (598 ~ 665 EC) a postulé que la Terre était une sphère et que les objets possédaient une affinité naturelle pour elle, tombant vers le centre de l'endroit où ils se trouvaient.
Les mouvements du Soleil, de notre Lune et des planètes sont également étudiés depuis des milliers d'années. Ces mouvements ont été décrits avec une précision étonnante par Ptolémée (90-168 de notre ère), dont la méthode des épicycles décrit les trajectoires des planètes sous la forme de cercles à l'intérieur de cercles. Cependant, rien ne prouve que quiconque ait établi un lien entre le mouvement des corps astronomiques et le mouvement des objets tombant sur Terre, jusqu'au XVIIe siècle.
Nicolas Copernic (1473—1543) est généralement considéré comme le premier à défier le système géocentrique (centré sur la Terre) de Ptolémée et à suggérer un système héliocentrique, dans lequel le Soleil est au centre du système solaire. Cette idée a été soutenue par les mesures incroyablement précises à l'œil nu des mouvements planétaires effectuées par Tycho Brahe et leur analyse par Johannes Kepler et Galileo Galilei. Kepler a montré que le mouvement de chaque planète est une ellipse (la première de ses trois lois, abordée dans Les lois du mouvement planétaire de Kepler), et Robert Hooke (le même Hooke qui a formulé la loi de Hooke pour les ressorts) a intuitivement suggéré que ces mouvements sont dus au fait que les planètes sont attirées par le Soleil. Cependant, c'est Isaac Newton qui a relié l'accélération des objets proches de la surface de la Terre à l'accélération centripète de la Lune sur son orbite autour de la Terre.
Enfin, dans la théorie de la gravité d'Einstein, nous examinons la théorie de la relativité générale proposée par Albert Einstein en 1916. Sa théorie s'inscrit dans une perspective très différente, selon laquelle la gravité est une manifestation de la déformation des masses dans l'espace et dans le temps. Les conséquences de sa théorie ont donné lieu à de nombreuses prédictions remarquables, qui ont pour l'essentiel toutes été confirmées au cours des nombreuses décennies qui ont suivi la publication de la théorie (y compris la mesure en 2015 des ondes gravitationnelles résultant de la fusion de deux trous noirs).
Loi de Newton sur la gravitation universelle
Newton a noté que les objets à la surface de la Terre (donc à une distance de R E du centre de la Terre) ont une accélération de g, mais que la Lune, à une distance d'environ 60 R E, a une accélération centripète environ (60) 2 fois plus petite que g. Il pourrait expliquer cela en postulant qu'une force existe entre deux objets quelconques, dont l'amplitude est donnée par le produit des deux masses divisé par le carré de la distance qui les sépare. Nous savons maintenant que cette loi carrée inverse est omniprésente dans la nature, fonction de la géométrie des sources ponctuelles. La force de toute source à une distance r est répartie sur la surface d'une sphère centrée autour de la masse. La surface de cette sphère est proportionnelle à r 2. Dans les chapitres suivants, nous verrons cette même forme dans la force électromagnétique.
La loi de la gravitation de Newton peut être exprimée comme
\[\vec{F}_{12} = G \frac{m_{1} m_{2}}{r^{2}} \hat{r}_{12} \label{13.1}\]
où\(\vec{F}_{12}\) est la force exercée sur l'objet 1 par l'objet 2 et\(\hat{r}_{12}\) est un vecteur unitaire qui pointe de l'objet 1 vers l'objet 2.
Comme le montre la figure\(\PageIndex{1}\), le\(\vec{F}_{12}\) vecteur pointe de l'objet 1 vers l'objet 2 et représente donc une force d'attraction entre les objets. La force égale mais opposée\(\vec{F}_{21}\) est la force exercée sur l'objet 2 par l'objet 1.
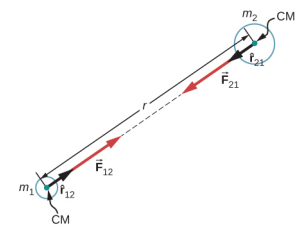
Ces forces égales mais opposées reflètent la troisième loi de Newton, dont nous avons parlé plus tôt. Notez qu'à proprement parler, l'équation \ ref {13.1} s'applique aux masses de points : toute la masse est située en un point. Mais elle s'applique également à tous les objets sphériquement symétriques, où r est la distance entre les centres de masse de ces objets. Dans de nombreux cas, cela fonctionne assez bien pour les objets non symétriques, si leur séparation est grande par rapport à leur taille, et si nous prenons r comme la distance entre le centre de masse de chaque corps.
L'expérience de Cavendish
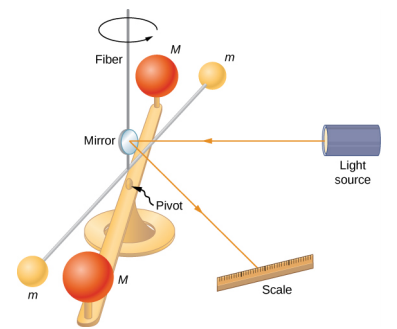
Un siècle après la publication par Newton de sa loi de la gravitation universelle, Henry Cavendish a déterminé la constante de proportionnalité G en effectuant une expérience minutieuse. Il a construit un dispositif similaire à celui de la figure\(\PageIndex{2}\), dans lequel de petites masses sont suspendues à un fil. Une fois en équilibre, deux masses fixes plus grandes sont placées symétriquement à proximité des plus petites. L'attraction gravitationnelle crée une torsion (torsion) dans le fil de support qui peut être mesurée.
La constante G est appelée constante gravitationnelle universelle et Cavendish l'a déterminée comme étant G = 6,67 x 10 −11 N • m 2 /kg 2. Le mot « universel » indique que les scientifiques pensent que cette constante s'applique à des masses de toutes compositions et qu'elle est la même dans tout l'Univers. La valeur de G est un nombre incroyablement petit, ce qui indique que la force de gravité est très faible. L'attraction entre des masses aussi petites que notre corps, ou même des objets de la taille d'un gratte-ciel, est incroyablement faible. Par exemple, deux masses de 1,0 kg situées à 1,0 mètre l'une de l'autre exercent une force de 6,7 x 10 -11 N l'une sur l'autre. Il s'agit du poids d'un grain de pollen typique.
Bien que la gravité soit la plus faible des quatre forces fondamentales de la nature, c'est sa nature attrayante qui nous tient à la Terre, amène les planètes à orbiter autour du Soleil et le Soleil à orbiter autour de notre galaxie, et lie les galaxies en amas, allant de quelques à des millions. La gravité est la force qui forme l'univers.
Pour déterminer le mouvement provoqué par la force gravitationnelle, procédez comme suit :
- Identifiez les deux masses, l'une ou les deux, pour lesquelles vous souhaitez déterminer la force gravitationnelle.
- Dessinez un diagramme de corps libre, en esquissant la force agissant sur chaque masse et en indiquant la distance entre leurs centres de masse.
- Appliquez la deuxième loi du mouvement de Newton à chaque masse pour déterminer comment elle se déplacera.
Prenons l'exemple de deux véhicules de charge utile Soyouz presque sphériques, en orbite autour de la Terre, chacun ayant une masse de 9 000 kg et un diamètre de 4,0 m. Ils sont initialement au repos l'un par rapport à l'autre, à 10 m de centre à centre. (Comme nous le verrons dans les lois du mouvement planétaire de Kepler, les deux orbitent autour de la Terre à la même vitesse et interagissent presque de la même manière que s'ils étaient isolés dans l'espace lointain.) Déterminez la force gravitationnelle entre eux et leur accélération initiale. Estimez le temps qu'il leur faut pour dériver ensemble et la vitesse à laquelle ils se déplacent au moment de l'impact.
Stratégie
Nous utilisons la loi de la gravitation de Newton pour déterminer la force entre les deux, puis nous utilisons la deuxième loi de Newton pour déterminer l'accélération de chacune d'elles. Pour l'estimation, nous supposons que cette accélération est constante et nous utilisons les équations d'accélération constante de Motion along a Straight Line pour déterminer l'heure et la vitesse de la collision.
Solution
L'ampleur de la force est
\[|\vec{F}_{12}| = F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{(9000\; kg)(9000\; kg)}{(10\; m)^{2}} = 5.4 \times 10^{-5}\; N \ldotp\]
L'accélération initiale de chaque charge utile est
\[a = \frac{F}{m} = \frac{5.4 \times 10^{-5}\; N}{9000\; kg} = 6.0 \times 10^{-9}\; m/s^{2} \ldotp\]
Les véhicules ont un diamètre de 4,0 m, de sorte qu'ils se déplacent de 10,0 m à 4,0 m l'un de l'autre, soit une distance de 3,0 m chacun. Un calcul similaire à celui ci-dessus, pour les véhicules distants de 4,0 m, donne une accélération de 3,8 x 10 −8 m/s 2, et la moyenne de ces deux valeurs est de 2,2 x 10 −8 m/s 2. Si nous supposons une accélération constante de cette valeur et qu'ils partent de l'arrêt, les véhicules entrent en collision avec la vitesse donnée par
\[v^{2} = v_{0}^{2} + 2a (x - x_{0}),\; where\; v_{0} = 0,\]
donc
\[v = \sqrt{2(2.2 \times 10^{-9}\; N)(3.0\; m)} = 3.6 \times 10^{-4}\; m/s \ldotp\]
Nous utilisons v = v 0 + at pour trouver t = v/a = 1,7 x 10 4 s soit environ 4,6 heures.
L'importance
Ces calculs, y compris la force initiale, ne sont que des estimations, car les véhicules ne sont probablement pas sphériquement symétriques. Mais vous pouvez voir que la force est incroyablement faible. Les astronautes doivent rester attachés lorsqu'ils travaillent à l'extérieur de l'immense Station spatiale internationale (ISS), comme le montre la figure\(\PageIndex{3}\), car l'attraction gravitationnelle ne peut les empêcher de s'éloigner le plus possible de la station.

Qu'arrive-t-il à la force et à l'accélération lorsque les véhicules tombent ensemble ? Quelle sera notre estimation de la vitesse lors d'une collision supérieure ou inférieure à la vitesse réelle ? Et enfin, que se passerait-il si les masses n'étaient pas identiques ? La force exercée sur chacun serait-elle la même ou différente ? Que diriez-vous de leurs accélérations ?
- Réponse
-
Ajoutez des textes ici. Ne supprimez pas ce texte au préalable.
L'effet de la gravité entre deux objets ayant des masses de l'ordre de ces véhicules spatiaux est en effet faible. Pourtant, l'effet de la gravité sur vous depuis la Terre est suffisamment important pour qu'une chute de quelques mètres seulement sur Terre puisse être dangereuse. Nous examinons la force de gravité près de la surface de la Terre dans la section suivante.
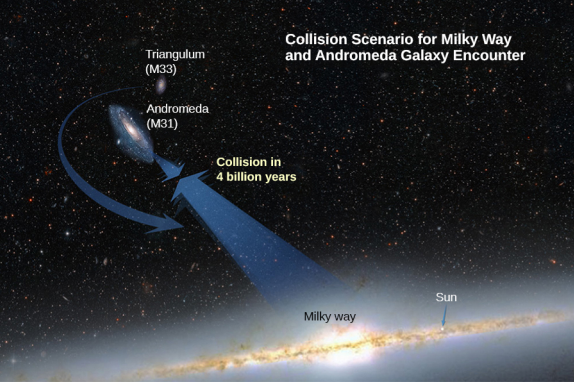
Découvrez l'accélération de notre galaxie, la Voie lactée, due à la galaxie de taille comparable la plus proche, la galaxie d'Andromède (Figure\(\PageIndex{4}\)). La masse approximative de chaque galaxie est de 800 milliards de masses solaires (une masse solaire est la masse de notre Soleil), séparées par 2,5 millions d'années-lumière. (Notez que la masse d'Andromède n'est pas très connue mais qu'on pense qu'elle est légèrement plus grande que notre galaxie.) Chaque galaxie a un diamètre d'environ 100 000 années-lumière (1 année-lumière = 9,5 x 10 15 m).

Stratégie
Comme dans l'exemple précédent, nous utilisons la loi de gravitation de Newton pour déterminer la force entre les deux, puis nous utilisons la deuxième loi de Newton pour déterminer l'accélération de la Voie lactée. On peut considérer les galaxies comme des masses ponctuelles, car leur taille est environ 25 fois plus petite que leur séparation. La masse du Soleil (voir l'annexe D) est de 2,0 x 10 30 kg et l'année-lumière est la distance parcourue par la lumière en un an, 9,5 x 10 15 m.
Solution
L'ampleur de la force est
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \frac{[(800 \times 10^{9})(2.0 \times 10^{30}\; kg)]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15}\; m)]^{2}} = 3.0 \times 10^{29}\; N \ldotp\]
L'accélération de la Voie lactée est
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30}\; kg)} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
L'importance
Cette valeur d'accélération vous paraît-elle étonnamment faible ? S'ils partent du repos, ils accéléreront directement l'un vers l'autre, « entrant en collision » au niveau de leur centre de gravité. Estimons le temps nécessaire pour que cela se produise. L'accélération initiale est d'environ 10 −13 m/s 2, donc en utilisant v = at, nous voyons qu'il faudrait environ 10 13 s pour que chaque galaxie atteigne une vitesse de 1,0 m/s, et qu'elles ne seraient plus proches que d'environ 0,5 x 10 13 m. C'est neuf ordres de grandeur inférieur à la distance initiale qui les sépare. En réalité, de tels mouvements sont rarement simples. Ces deux galaxies, ainsi qu'une cinquantaine d'autres galaxies plus petites, sont toutes liées gravitationnellement à notre amas local. Notre cluster local est lié gravitationnellement à d'autres clusters dans ce que l'on appelle un supercluster. Tout cela fait partie de la grande danse cosmique qui résulte de la gravitation, comme le montre la figure\(\PageIndex{5}\).