13.4 : Énergie potentielle gravitationnelle et énergie totale
- Page ID
- 191301
- Déterminer les variations de l'énergie potentielle gravitationnelle sur de grandes distances
- Appliquer la conservation de l'énergie pour déterminer la vitesse d'échappement
- Déterminer si les corps astronomiques sont liés par la gravitation
Nous avons étudié l'énergie potentielle gravitationnelle dans Énergie potentielle et conservation de l'énergie, où la valeur de\(g\) est restée constante. Nous développons maintenant une expression qui fonctionne sur des distances telles que g n'est pas constant. Cela est nécessaire pour calculer correctement l'énergie nécessaire pour placer des satellites en orbite ou pour les envoyer en mission dans l'espace.
Énergie potentielle gravitationnelle au-delà de la Terre
Nous avons défini précédemment le travail et l'énergie potentielle. L'utilité de ces définitions réside dans la facilité avec laquelle nous pouvons résoudre de nombreux problèmes grâce aux économies d'énergie. L'énergie potentielle est particulièrement utile pour les forces qui changent avec la position, comme le fait la force gravitationnelle sur de grandes distances. Dans Potential Energy and Conservation of Energy, nous avons montré que le changement de l'énergie potentielle gravitationnelle près de la surface de la Terre est
\[ \Delta U = mg(y_2− y_1) \label{simple}\]
Cela fonctionne très bien s'il\(g\) ne change pas de manière significative entre y 1 et y 2. Nous revenons à la définition du travail et de l'énergie potentielle pour en déduire une expression correcte sur de plus grandes distances. Rappelons que le travail (W) est l'intégrale du produit scalaire entre la force et la distance. Essentiellement, c'est le produit de la composante d'une force le long d'un déplacement par ce déplacement. Nous définissons\(\Delta u\) comme le négatif du travail effectué par la force que nous associons à l'énergie potentielle. Pour plus de clarté, nous dérivons une expression pour déplacer une masse m de la distance r 1 du centre de la Terre à la distance r 2. Cependant, le résultat peut facilement être généralisé à deux objets quelconques modifiant leur séparation d'une valeur à l'autre.
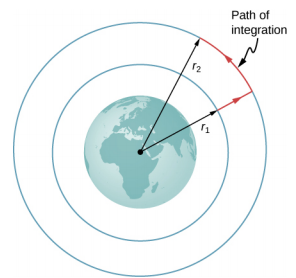
Considérez la Figure\(\PageIndex{1}\), dans laquelle nous prenons m d'une distance r 1 du centre de la Terre à une distance r 2 du centre. La gravité est une force conservatrice (son amplitude et sa direction dépendent uniquement de la localisation), nous pouvons donc emprunter la trajectoire que nous voulons, et le résultat du calcul du travail est le même. Nous suivons le chemin indiqué, car cela simplifie grandement l'intégration. Nous nous déplaçons d'abord radialement vers l'extérieur de la distance r 1 à la distance r 2, puis nous nous déplaçons le long de l'arc de cercle jusqu'à atteindre la position finale. Pendant la partie radiale,\(\vec{F}\) est opposée à la direction que nous parcourons le long de d\(\vec{r}\), donc
\[E = K_1 + U_1 = K_2 + U_2\]
Le long de l'arc,\(\vec{F}\) est perpendiculaire à d\(\vec{r}\), donc\(\vec{F}\; \cdotp d \vec{r}\) = 0. Aucun travail n'est effectué lorsque nous nous déplaçons le long de l'arc. En utilisant l'expression de la force gravitationnelle et en notant les valeurs pour\(\vec{F}\; \cdotp d \vec{r}\) le long des deux segments de notre trajectoire, nous avons
\[ \begin{align} \Delta U &= - \int_{r_{1}}^{r_{2}} \vec{F}\; \cdotp d \vec{r} \\[4pt] &= GM_{E} m \int_{r_{1}}^{r_{2}} \frac{dr}{r^{2}} \\[4pt] &= GM_{E} m \left(\dfrac{1}{r_{1}} - \dfrac{1}{r_{2}}\right) \ldotp \label{eq13.3} \end{align} \]
Puisque\(\Delta U = U_2 − U_1\) nous pouvons adopter une expression simple pour\(U\) :
\[U = - \frac{GM_{E} m}{r} \ldotp \label{13.4}\]
Notez deux éléments importants avec cette définition. Tout d'abord,\(U → 0\) comme\(r → \infty\). L'énergie potentielle est nulle lorsque les deux masses sont infiniment éloignées. Seule la différence\(U\) est importante, de sorte que le choix de\(U = 0\) la forme n'\(r = \infty\)est qu'une question de commodité. (Rappelez-vous que lors de problèmes de gravité antérieurs, vous étiez libre de le prendre\(U = 0\) en haut ou en bas d'un bâtiment, ou n'importe où.) Ensuite, notez que cela\(U\) devient de plus en plus négatif à mesure que les masses se rapprochent. Cela correspond à ce que vous avez appris sur l'énergie potentielle dans Énergie potentielle et conservation de l'énergie. Lorsque les deux masses sont séparées, un travail positif doit être effectué contre la force de gravité et, par conséquent,\(U\) augmente (devient moins négatif). Toutes les masses tombent naturellement ensemble sous l'influence de la gravité, passant d'une énergie potentielle plus élevée à une énergie potentielle plus faible.
Quelle quantité d'énergie est nécessaire pour soulever le véhicule Soyouz de 9000 kg de la surface de la Terre jusqu'à la hauteur de l'ISS, à 400 km au-dessus de la surface ?
Stratégie
Utilisez l'équation \ ref {eq13.3} pour déterminer la variation de l'énergie potentielle de la charge utile. Cette quantité de travail ou d'énergie doit être fournie pour soulever la charge utile.
Solution
Si l'on tient compte du fait que nous commençons à la surface de la Terre et que nous nous terminons à 400 km au-dessus de la surface de la Terre, le changement\(U\) de
Nous insérons les valeurs
- \(m = 9000\; kg\)
- \(M_{E} = 5.96 \times 10^{24}\; kg\)
- \(R_{E} = 6.37 \times 10^{6}\; m\)
et convertissez 400 km en 4,00 x 10 5 m. Nous trouvons\(\Delta U = 3.32 \times 10^{10} J\). C'est positif et indique une augmentation de l'énergie potentielle, comme on pouvait s'y attendre.
L'importance
Pour mettre en perspective, considérez que la consommation moyenne d'énergie des ménages américains en 2013 était de 909 kWh par mois. C'est l'énergie de
\[909\; kWh \times 1000\; W/kW \times 3600\; s/h = 3.27 \times 10^{9}\; J\; per\; month \ldotp \nonumber\]
Notre résultat est donc une dépense énergétique équivalente à 10 mois. Cependant, il s'agit simplement de l'énergie nécessaire pour augmenter la charge utile de 400 km. Si nous voulons que le Soyouz soit en orbite pour rejoindre l'ISS et ne pas simplement retomber sur Terre, il a besoin de beaucoup d'énergie cinétique. Comme nous le verrons dans la section suivante, cette énergie cinétique est environ cinq fois supérieure à celle de\(\Delta\) U. De plus, beaucoup plus d'énergie est dépensée pour soulever le système de propulsion lui-même. Les voyages spatiaux ne sont pas bon marché.
Pourquoi ne pas utiliser plutôt l'expression la plus simple dans Equation \ ref {simple} ? Quelle serait l'importance de l'erreur ? (La valeur\(g\) à 400 km au-dessus de la Terre est de 8,67 m/s 2.)
Conservation de l'énergie
Dans Énergie potentielle et conservation de l'énergie, nous avons décrit comment appliquer la conservation de l'énergie aux systèmes soumis à des forces conservatrices. Nous avons pu résoudre de nombreux problèmes, notamment ceux liés à la gravité, en utilisant plus simplement les économies d'énergie. Ces principes et stratégies de résolution de problèmes s'appliquent tout aussi bien ici. Le seul changement consiste à placer la nouvelle expression de l'énergie potentielle dans l'équation de conservation de l'énergie,
\[E_{tot} = K_1 + U_1 = K_2 + U_2.\]
\[\frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \label{13.5}\]
Notez que nous utilisons M, plutôt que M E, pour nous rappeler que nous ne sommes pas limités aux problèmes impliquant la Terre. Cependant, nous supposons toujours que m << M. (Pour les problèmes où cela n'est pas vrai, nous devons inclure l'énergie cinétique des deux masses et utiliser la conservation de l'élan pour relier les vitesses entre elles. Mais le principe reste le même.)
Vitesse d'échappement
La vitesse d'échappement est souvent définie comme étant la vitesse initiale minimale d'un objet qui est requise pour s'échapper de la surface d'une planète (ou de tout corps de grande taille comme une lune) et ne jamais revenir. Comme d'habitude, nous supposons qu'aucune énergie n'est perdue dans l'atmosphère, s'il y en a une.
Prenons le cas où un objet est lancé depuis la surface d'une planète avec une vitesse initiale dirigée loin de la planète. Avec la vitesse minimale nécessaire pour s'échapper, l'objet s'immobiliserait à l'infini, c'est-à-dire qu'il abandonnerait la dernière de son énergie cinétique juste au moment où il atteint l'infini, où la force de gravité devient nulle. Puisque U → 0 est r →\(\infty\), cela signifie que l'énergie totale est nulle. Ainsi, nous trouvons la vitesse d'échappement de la surface d'un corps astronomique de masse M et de rayon R en réglant l'énergie totale à zéro. À la surface du corps, l'objet se trouve à une vitesse d'échappement\(r_1 = R\) et il a une vitesse de fuite\(v_1 = v_{esc}\). Il atteint\(r_2 = \infty\) avec vélocité\(v_2 = 0\). En le remplaçant par l'équation \ ref {13.5}, nous avons
\[\frac{1}{2} mv_{esc}^{2} - \frac{GMm}{R} = \frac{1}{2} m0^{2} - \frac{GMm}{\infty} = 0 \ldotp\]
Résoudre la question de la vitesse d'échappement,
\[v_{esc} = \sqrt{\frac{2GM}{R}} \ldotp \label{13.6}\]
Remarquez que l'équation\(m\) a été annulée. La vitesse d'échappement est la même pour tous les objets, quelle que soit leur masse. De plus, nous ne sommes pas limités à la surface de la planète ; R peut être n'importe quel point de départ au-delà de la surface de la planète.
Quelle est la vitesse d'évacuation de la surface de la Terre ? Supposons qu'il n'y ait pas de perte d'énergie due à la résistance Comparez cela à la vitesse d'échappement du Soleil, à partir de l'orbite de la Terre.
Stratégie
Nous utilisons l'équation 13.6, qui définit clairement les valeurs de R et M. Pour échapper à la Terre, nous avons besoin de la masse et du rayon de la Terre. Pour échapper au Soleil, nous avons besoin de la masse du Soleil et de la distance orbitale entre la Terre et le Soleil.
Solution
En substituant les valeurs de la masse et du rayon de la Terre directement dans l'équation 13.6, nous obtenons
\[ \begin {align*} v_{esc} &= \sqrt{\frac{2GM}{R}} \\[4pt] &= \sqrt{\frac{2 (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{6.37 \times 10^{6}\; m}} \\[4pt] &= 1.12 \times 10^{4}\; m/s \ldotp \end{align*}\]
Cela représente environ 11 km/s ou 25 000 mi/h. Pour échapper au Soleil, en partant de l'orbite de la Terre, nous utilisons R = R ES = 1,50 x 10 11 m et M Sun = 1,99 x 10 30 kg. Le résultat est v esc = 4,21 x 10 4 m/s, soit environ 42 km/s.
L'importance
La vitesse nécessaire pour échapper au Soleil (quitter le système solaire) est presque quatre fois supérieure à la vitesse d'échappement de la surface de la Terre. Mais il y a de l'aide dans les deux cas. La Terre tourne à une vitesse de près de 1,7 km/s à l'équateur, et nous pouvons utiliser cette vitesse pour nous échapper ou pour atteindre l'orbite. Pour cette raison, de nombreuses entreprises spatiales commerciales entretiennent des installations de lancement à proximité de l'équateur. Pour échapper au soleil, il y a encore plus d'aide. La Terre tourne autour du Soleil à une vitesse d'environ 30 km/s. En lançant dans la direction du mouvement de la Terre, nous n'avons besoin que de 12 km/s supplémentaires. L'utilisation de l'assistance gravitationnelle d'autres planètes, essentiellement une technique de lance-pierre gravitationnelle, permet aux sondes spatiales d'atteindre des vitesses encore plus élevées. Dans cette technique de lance-pierre, le véhicule s'approche de la planète et est accéléré par l'attraction gravitationnelle de la planète. Il atteint sa vitesse maximale au point d'approche le plus proche, mais il décélère dans la même mesure lorsqu'il s'éloigne. Mais par rapport à la planète, la vitesse du véhicule est la même bien avant l'approche et longtemps après. Si les directions sont choisies correctement, cela peut entraîner une augmentation significative (ou une diminution si nécessaire) de la vitesse du véhicule par rapport au reste du système solaire.
Énergie et objets liés par la gravitation
Comme indiqué précédemment, la vitesse d'échappement peut être définie comme la vitesse initiale d'un objet qui peut s'échapper de la surface d'une lune ou d'une planète. Plus généralement, il s'agit de la vitesse à n'importe quelle position telle que l'énergie totale soit nulle. Si l'énergie totale est nulle ou supérieure, l'objet s'échappe. Si l'énergie totale est négative, l'objet ne peut pas s'échapper. Voyons pourquoi c'est le cas.
Comme indiqué précédemment, nous voyons cela\(U → 0\) comme\(r → \infty\). Si l'énergie totale est nulle, alors que m atteint une valeur de r proche de l'infini, U devient nul, de même que l'énergie cinétique. Ainsi, m s'arrête infiniment loin de M. Il « vient de s'échapper » M. Si l'énergie totale est positive, alors l'énergie cinétique reste à zéro\(r = \infty\) et m ne revient certainement pas. Lorsque l'énergie totale est nulle ou supérieure, on dit que m n'est pas lié gravitationnellement à M.
D'autre part, si l'énergie totale est négative, alors l'énergie cinétique doit atteindre zéro à une valeur finie de r, où U est négatif et égal à l'énergie totale. L'objet ne peut jamais dépasser cette distance finie par rapport à M, car cela nécessiterait que l'énergie cinétique devienne négative, ce qui n'est pas possible. Nous disons que m est lié gravitationnellement à M.
Nous avons simplifié cette discussion en supposant que l'objet s'éloignait directement de la planète. Ce qui est remarquable, c'est que le résultat s'applique à n'importe quelle vitesse. L'énergie est une quantité scalaire et, par conséquent, l'équation \ ref {13.5} est une équation scalaire : la direction de la vitesse ne joue aucun rôle dans la conservation de l'énergie. Il est possible d'avoir un système gravitationnel dans lequel les masses ne « tombent pas ensemble », mais entretiennent un mouvement orbital l'une par rapport à l'autre.
Nous avons une dernière observation importante. Nous avons indiqué précédemment que si l'énergie totale est nulle ou supérieure, l'objet s'échappe. À proprement parler, l'équation \ ref {13.5} et l'équation \ ref {13.6} s'appliquent aux objets ponctuels. Elles s'appliquent également aux objets sphériquement symétriques de taille finie,\(r\) à condition que la valeur de l'équation \ ref {13.5} soit toujours supérieure à la somme des rayons des deux objets. Si r devient inférieur à cette somme, les objets entrent en collision. (Même pour des valeurs de r plus élevées, mais proches de la somme des rayons, les forces de marée gravitationnelles peuvent avoir des effets significatifs si les deux objets ont la taille d'une planète. Nous examinons les effets des marées sur les forces des marées.) Ni l'énergie totale positive ni négative n'empêche des masses de taille finie d'entrer en collision. Pour les objets réels, l'orientation est importante.
Reprenons l'exemple précédent, où nous avons calculé la vitesse d'échappement entre la Terre et le Soleil, à partir de l'orbite de la Terre. Nous avons remarqué que la Terre a déjà une vitesse orbitale de 30 km/s, soit la vitesse tangentielle nécessaire pour rester en orbite circulaire, comme nous le verrons dans la section suivante. Si un objet avait cette vitesse à la distance de l'orbite de la Terre, mais s'éloignait directement du Soleil, quelle distance parcourrait-il avant de s'immobiliser ? Ignorez les effets gravitationnels de tout autre corps.
Stratégie
L'objet possède des énergies cinétiques et potentielles initiales que nous pouvons calculer. Lorsque sa vitesse atteint zéro, il est à sa distance maximale du Soleil. Nous utilisons l'équation 13.5, conservation de l'énergie, pour déterminer la distance à laquelle l'énergie cinétique est nulle.
Solution
La position initiale de l'objet est le rayon de l'orbite de la Terre et la vitesse initiale est donnée comme 30 km/s. La vitesse finale est nulle, de sorte que nous pouvons déterminer la distance à ce point à partir de l'équation de conservation de l'énergie. En utilisant R ES = 1,50 x 10 11 m et M Sun = 1,99 x 10 30 kg, nous avons
\[\begin{split} \frac{1}{2} mv_{1}^{2} - \frac{GMm}{r_{1}} & = \frac{1}{2} mv_{2}^{2} - \frac{GMm}{r_{2}} \\ \frac{1}{2} \cancel{m} (30\; km/s)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{1.50 \times 10^{11}\; m} & = \frac{1}{2} m(0)^{2} - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(1.99 \times 10^{30}\; kg) \cancel{m}}{r_{2}} \end{split}\]
où la masse m s'annule. En résolvant r 2, on obtient r 2 = 3,0 x 10 11 m. Notez que c'est le double de la distance initiale par rapport au Soleil et que cela nous amène au-delà de l'orbite de Mars, mais pas tout à fait jusqu'à la ceinture d'astéroïdes.
L'importance
Dans ce cas, l'objet a atteint une distance exactement le double de la distance orbitale initiale. Nous en verrons la raison dans la section suivante lorsque nous calculerons la vitesse pour les orbites circulaires.
Supposons que vous vous trouviez dans un vaisseau spatial en orbite autour du Soleil sur l'orbite de la Terre, mais loin de la Terre (pour que cela puisse être ignoré). Comment pourriez-vous rediriger votre vitesse tangentielle vers la direction radiale afin de pouvoir ensuite passer par l'orbite de Mars ? Que faudrait-il pour modifier uniquement la direction de la vitesse ?


