13.5 : Orbites et énergie des satellites
- Page ID
- 191295
- Décrire le mécanisme des orbites circulaires
- Trouvez les périodes orbitales et les vitesses des satellites
- Déterminez si les objets sont liés par gravité
La Lune tourne autour de la Terre. À leur tour, la Terre et les autres planètes gravitent autour du Soleil. L'espace situé directement au-dessus de notre atmosphère est rempli de satellites artificiels en orbite. Nous examinons la plus simple de ces orbites, l'orbite circulaire, afin de comprendre la relation entre la vitesse et la période des planètes et des satellites par rapport à leurs positions et aux corps sur lesquels ils orbitent.
Orbites circulaires
Comme indiqué au début de ce chapitre, Nicolas Copernic a d'abord suggéré que la Terre et toutes les autres planètes orbitent autour du Soleil en cercles. Il a également noté que les périodes orbitales augmentaient avec la distance par rapport au Soleil. Des analyses ultérieures effectuées par Kepler ont montré que ces orbites sont en fait des ellipses, mais que les orbites de la plupart des planètes du système solaire sont presque circulaires. La distance orbitale entre la Terre et le Soleil ne varie que de 2 %. L'exception est l'orbite excentrique de Mercure, dont la distance orbitale varie de près de 40 %.
La détermination de la vitesse orbitale et de la période orbitale d'un satellite est beaucoup plus facile pour les orbites circulaires, c'est pourquoi nous faisons cette hypothèse dans la dérivation qui suit. Comme nous l'avons décrit dans la section précédente, un objet dont l'énergie totale est négative est lié par la gravitation et se trouve donc en orbite. Nos calculs pour le cas particulier des orbites circulaires le confirmeront. Nous nous concentrons sur les objets en orbite autour de la Terre, mais nos résultats peuvent être généralisés pour d'autres cas.
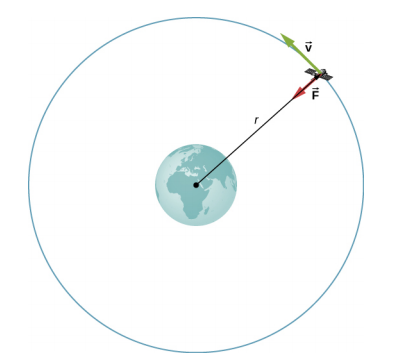
Prenons l'exemple d'un satellite de masse m sur une orbite circulaire autour de la Terre à\(r\) distance du centre de la Terre (Figure\(\PageIndex{1}\)). Il possède une accélération centripète dirigée vers le centre de la Terre. La gravité de la Terre est la seule force agissant, donc la deuxième loi de Newton donne
\[\frac{GmM_{E}}{r^{2}} = ma_{c} = \frac{mv_{orbit}^{2}}{r} \ldotp\]
Nous résolvons la vitesse de l'orbite, en notant que cela\(m\) annule, pour obtenir la vitesse orbitale
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} \ldotp \label{13.7}\]
Conformément à ce que nous avons vu dans\(g = G \frac{M_E}{r^2}\) et\(v_{esc} = \sqrt{\frac{2GM}{R}}\), m n'apparaît pas dans l'équation \ ref {13.7}. La valeur de g, la vitesse d'échappement et la vitesse orbitale dépendent uniquement de la distance par rapport au centre de la planète, et non de la masse de l'objet sur lequel on agit. Remarquez la similitude des équations pour v orbit et v esc. La vitesse d'échappement est exactement\(\sqrt{2}\) fois supérieure, environ 40 %, à la vitesse orbitale. Cette comparaison a été constatée dans l'exemple 13.4.2, et elle est vraie pour un satellite à n'importe quel rayon.
Pour connaître la période d'une orbite circulaire, on note que le satellite parcourt la circonférence de l'orbite\( 2\pi r\) en une période\(T\). En utilisant la définition de la vitesse, nous avons
\[v_{orbit} = \frac{2 \pi r}{T}.\]
Nous la remplaçons dans l'équation \ ref {13.7} et la réorganisons pour obtenir
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.8}\]
Nous verrons dans la section suivante qu'il s'agit de la troisième loi de Kepler pour le cas des orbites circulaires. Cela confirme également l'observation de Copernic selon laquelle la période d'une planète augmente à mesure que l'on s'éloigne du Soleil. Il suffit de remplacer\(M_E\) par\(M_{Sun}\) dans l'équation \ ref {13.8}.
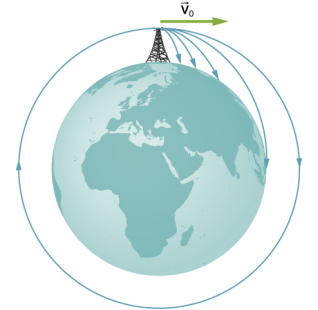
Nous concluons cette section en revenant à notre discussion précédente sur les astronautes en orbite qui semblent en apesanteur, comme s'ils tombaient librement vers la Terre. En fait, ils sont en chute libre. Examinez les trajectoires illustrées dans la figure\(\PageIndex{2}\). (Cette figure est basée sur un dessin de Newton dans son Principia et est également apparue plus tôt dans Motion in Two and Three Dimensions.) Toutes les trajectoires présentées qui touchent la surface de la Terre ont une vitesse inférieure à la vitesse orbitale. Les astronautes accéléraient vers la Terre en suivant les trajectoires non circulaires indiquées et se sentaient en apesanteur. (En fait, les astronautes s'entraînent pour la vie en orbite en pilotant des avions qui tombent librement pendant 30 secondes d'affilée.) Mais avec la vitesse orbitale correcte, la surface de la Terre s'en éloigne exactement au même rythme qu'elle tombe vers la Terre. Bien entendu, rester à la même distance de la surface est le point d'une orbite circulaire.
Nous pouvons résumer notre discussion sur les satellites en orbite dans la stratégie de résolution de problèmes suivante.
- Déterminez si les équations de vitesse, d'énergie ou de période sont valides pour le problème en question. Si ce n'est pas le cas, commencez par les premiers principes que nous avons utilisés pour établir ces équations.
- Pour partir des principes de base, dessinez un diagramme du corps libre et appliquez la loi de la gravitation de Newton et la deuxième loi de Newton.
- En plus des définitions de la vitesse et de l'énergie, appliquez la deuxième loi du mouvement de Newton aux corps qui vous intéressent.
Déterminez la vitesse et la période orbitales de la Station spatiale internationale (ISS).
Stratégie
Comme l'ISS orbite à 4,00 x 10 2 km au-dessus de la surface de la Terre, son rayon d'orbite est R E + 4,00 x 10 2 km. Nous utilisons les équations \ ref {13.7} et \ ref {13.8} pour trouver la vitesse orbitale et la période, respectivement.
Solution
En utilisant l'équation \ ref {13.7}, la vitesse orbitale est
\[v_{orbit} = \sqrt{\frac{GM_{E}}{r}} = \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} = 7.67 \times 10^{3}\; m/s\]
soit environ 17 000 mi/h. En utilisant l'équation \ ref {13.8}, la période est
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} = 2 \pi \sqrt{\frac{(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}} = 5.55 \times 10^{3}\; s\]
ce qui représente un peu plus de 90 minutes.
L'importance
L'ISS est considérée comme étant en orbite terrestre basse (LEO). Presque tous les satellites sont en orbite basse, y compris la plupart des satellites météorologiques. Les satellites GPS, situés à environ 20 000 km, sont considérés comme une orbite terrestre moyenne. Plus l'orbite est haute, plus il faut d'énergie pour la placer et plus il faut d'énergie pour l'atteindre à des fins de réparation. Les satellites en orbite géosynchrone présentent un intérêt particulier. Toutes les antennes paraboliques fixes au sol orientées vers le ciel, telles que les antennes de réception de télévision, sont orientées vers des satellites géosynchrones. Ces satellites sont placés à la distance exacte, juste au-dessus de l'équateur, de telle sorte que leur période d'orbite est d'un jour. Ils restent dans une position fixe par rapport à la surface de la Terre.
De quel facteur le rayon doit-il changer pour réduire de moitié la vitesse orbitale d'un satellite ? Par quel facteur cela changerait-il la période ?
Déterminez la masse de la Terre à partir de l'orbite de la Lune.
Stratégie
Nous utilisons l'équation \ ref {13.8}, résolvons M E et la substituons à la période et au rayon de l'orbite. Le rayon et la période de l'orbite de la Lune ont été mesurés avec une précision raisonnable il y a des milliers d'années. D'après les données astronomiques de l'annexe D, la période de la Lune est de 27,3 jours = 2,36 x 10 6 s, et la distance moyenne entre les centres de la Terre et de la Lune est de 384 000 km.
Solution
Résoudre pour\(M_E\),
\[\begin{split} T & = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \\ M_{E} & = \frac{2 \pi^{2} r^{3}}{GT^{2}} = \frac{4 \pi^{2} (3.84 \times 10^{8}\; m)^{3}}{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.36 \times 10^{6}\; s)^{2}} = 6.01 \times 10^{24}\; kg \ldotp \end{split}\]
L'importance
Comparez cela à la valeur de 5,96 x 10 24 kg que nous avons obtenue dans l'exemple 13.3.3, en utilisant la valeur de\(g\) à la surface de la Terre. Bien que ces valeurs soient très proches (~ 0,8 %), les deux calculs utilisent des valeurs moyennes. La valeur de g varie de l'équateur aux pôles d'environ 0,5 %. Mais la Lune a une orbite elliptique sur laquelle la valeur de r varie d'un peu plus de 10 %. (La taille apparente de la pleine lune varie en fait d'environ cette quantité, mais il est difficile de la remarquer par une observation fortuite, car le temps d'un extrême à l'autre est de plusieurs mois.)
Ce dernier calcul de M E comporte une autre considération. Nous avons dérivé l'équation \ ref {13.8} en supposant que le satellite tourne autour du centre du corps astronomique au même rayon que celui utilisé dans l'expression de la force gravitationnelle entre eux. Quelle hypothèse est avancée pour justifier cela ? La Terre est environ 81 fois plus massive que la Lune. La Lune orbite-t-elle autour du centre exact de la Terre ?
Revoyons l'exemple 13.2.2. Supposons que les galaxies de la Voie lactée et d'Andromède se trouvent sur une orbite circulaire l'une autour de l'autre. Quelle serait la vitesse de chacun et quelle serait la durée de leur période orbitale ? Supposons que la masse de chacune soit de 800 milliards de masses solaires et que leurs centres soient séparés par 2,5 millions d'années-lumière.
Stratégie
Nous ne pouvons pas utiliser les équations \ ref {13.7} et \ ref {13.8} directement parce qu'elles ont été dérivées en supposant que l'objet de masse m orbitait autour du centre d'une planète de masse M beaucoup plus grande. Nous avons déterminé la force gravitationnelle dans l'exemple 13.2.2 en utilisant la loi de gravitation universelle de Newton. Nous pouvons utiliser la deuxième loi de Newton, appliquée à l'accélération centripète de l'une ou l'autre galaxie, pour déterminer leur vitesse tangentielle. À partir de ce résultat, nous pouvons déterminer la période de l'orbite.
Solution
Dans l'exemple 13.2.2, nous avons trouvé que la force entre les galaxies était
\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})\frac{[(800 \times 10^{9})(2.0 \times 10^{30})\; kg]^{2}}{[(2.5 \times 10^{6})(9.5 \times 10^{15})\; m]^{2}} = 3.0 \times 10^{29}\; N\]
et que l'accélération de chaque galaxie est
\[a = \frac{F}{m} = \frac{3.0 \times 10^{29}\; N}{(800 \times 10^{9})(2.0 \times 10^{30})\; kg} = 1.9 \times 10^{-13}\; m/s^{2} \ldotp\]
Comme les galaxies sont sur une orbite circulaire, elles ont une accélération centripète. Si nous ignorons l'effet des autres galaxies, alors, comme nous l'avons appris dans Momentum linéaire et collisions et Rotation à axe fixe, les centres de masse des deux galaxies restent fixes. Les galaxies doivent donc graviter autour de ce centre de masse commun. Pour des masses égales, le centre de gravité se trouve exactement à mi-chemin entre elles. Ainsi, le rayon de l'orbite, ou orbite, n'est pas le même que la distance entre les galaxies, mais la moitié de cette valeur, soit 1,25 million d'années-lumière. Ces deux valeurs différentes sont illustrées sur la figure\(\PageIndex{3}\).

En utilisant l'expression pour l'accélération centripète, nous avons
\[\begin{split} a_{c} & = \frac{v_{orbit}^{2}}{r_{orbit}} \\ 1.9 \times 10^{-13}\; m/s^{2} & = \frac{v_{orbit}^{2}}{(1.25 \times 10^{6})(9.5 \times 10^{15})\; m} \ldotp \end{split}\]
Nous avons résolu la vitesse de l'orbite\(v_{orbit} = 47\, km/s\). Enfin, nous pouvons déterminer la période de l'orbite directement à partir de
\[T = \frac{2 \pi r}{v_{orbit}}\]
pour déterminer que la période est T = 1,6 x 10 18 s, soit environ 50 milliards d'années.
L'importance
La vitesse orbitale de 47 km/s peut sembler élevée au premier abord. Mais cette vitesse est comparable à la vitesse d'échappement du Soleil, que nous avons calculée dans un exemple précédent. Pour donner encore plus de perspective, cette période est presque quatre fois plus longue que la durée d'existence de l'Univers.
En fait, le mouvement relatif actuel de ces deux galaxies est tel qu'elles devraient entrer en collision dans environ 4 milliards d'années. Bien que la densité des étoiles dans chaque galaxie rende improbable la collision directe de deux étoiles, une telle collision aura un effet dramatique sur la forme des galaxies. Des exemples de telles collisions sont bien connus en astronomie.
Les galaxies ne sont pas des objets uniques. Comment la force gravitationnelle d'une galaxie exercée sur les étoiles « les plus proches » de l'autre galaxie se compare-t-elle à celles qui s'exercent plus loin ? Quel effet cela aurait-il sur la forme des galaxies elles-mêmes ?
Consultez la page Sloan Digital Sky Survey pour plus d'informations sur les collisions de galaxies.
Utilisez cette simulation interactive pour déplacer le Soleil, la Terre, la Lune et la station spatiale afin de voir les effets sur leurs forces gravitationnelles et leurs trajectoires orbitales. Visualisez les tailles et les distances entre les différents corps célestes et désactivez la gravité pour voir ce qui se passerait sans elle.
Énergie sur des orbites circulaires
Dans Énergie potentielle gravitationnelle et énergie totale, nous avons soutenu que les objets sont liés par la gravitation si leur énergie totale est négative. L'argument était basé sur le cas simple où la vitesse était directement éloignée ou dirigée vers la planète. Nous examinons maintenant l'énergie totale pour une orbite circulaire et montrons qu'en effet, l'énergie totale est négative. Comme nous l'avons fait précédemment, nous commençons par la deuxième loi de Newton appliquée à une orbite circulaire,
\[\begin{split} \frac{GmM_{E}}{r^{2}} & = ma_{c} = \frac{mv^{2}}{r} \\ \frac{GmM_{E}}{r} & = mv^{2} \ldotp \end{split}\]
Dans la dernière étape, nous avons multiplié par de chaque\(r\) côté. Le côté droit contient juste le double de l'énergie cinétique, donc nous avons
\[K = \frac{1}{2} mv^{2} = \frac{GmM_{E}}{2r} \ldotp\]
L'énergie totale est la somme des énergies cinétique et potentielle, donc notre résultat final est
\[E = K + U = \frac{GmM_{E}}{2r} - \frac{GmM_{E}}{r} = - \frac{GmM_{E}}{2r} \ldotp \label{13.9}\]
Nous pouvons voir que l'énergie totale est négative, avec la même amplitude que l'énergie cinétique. Pour les orbites circulaires, l'amplitude de l'énergie cinétique est exactement la moitié de l'amplitude de l'énergie potentielle. Fait remarquable, ce résultat s'applique à deux masses quelconques sur des orbites circulaires autour de leur centre de masse commun, à une distance r l'une de l'autre. La preuve en est présentée sous forme d'exercice. Nous verrons dans la section suivante qu'une expression très similaire s'applique dans le cas des orbites elliptiques.
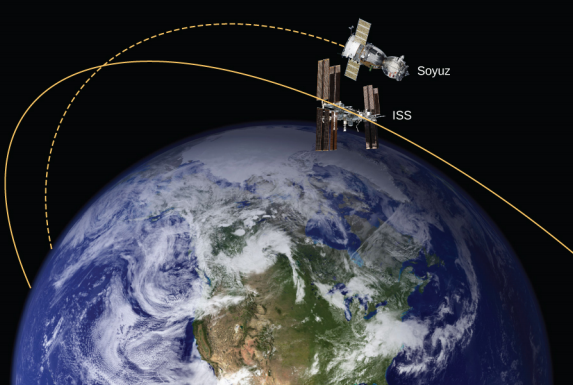
Dans l'exemple 13.4.1, nous avons calculé l'énergie requise pour simplement soulever le véhicule Soyouz de 9 000 kg de la surface de la Terre jusqu'à la hauteur de l'ISS, à 400 km au-dessus de la surface de la Terre. En d'autres termes, nous avons constaté son changement dans l'énergie potentielle. Nous nous demandons maintenant quel changement d'énergie total du véhicule Soyouz est nécessaire pour le sortir de la surface de la Terre et le mettre en orbite avec l'ISS pour un rendez-vous (Figure\(\PageIndex{4}\)). Quelle part de cette énergie totale est de l'énergie cinétique ?
Stratégie
L'énergie requise est la différence entre l'énergie totale du Soyouz en orbite et celle à la surface de la Terre. Nous pouvons utiliser l'équation \ ref {13.9} pour déterminer l'énergie totale du Soyouz sur l'orbite de l'ISS. Mais l'énergie totale à la surface est simplement l'énergie potentielle, puisqu'elle part du repos. [Notez que nous n'utilisons pas l'équation \ ref {13.9} à la surface, car nous ne sommes pas en orbite à la surface.] L'énergie cinétique peut ensuite être déterminée à partir de la différence entre la variation d'énergie totale et la variation de l'énergie potentielle constatée dans l'exemple 13.4.1. Nous pouvons également utiliser l'équation \ ref {13.7} pour trouver l'orbite v et calculer l'énergie cinétique directement à partir de celle-ci. L'énergie totale requise est alors l'énergie cinétique plus la variation de l'énergie potentielle trouvée dans l'exemple 13.4.1.
Solution
D'après l'équation \ ref {13.9}, l'énergie totale du Soyouz sur la même orbite que l'ISS est
\[\begin{split} E_{orbit} & = K_{orbit} + U_{orbit} = - \frac{GmM_{E}}{2r} \\ & = \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{2(6.36 \times 10^{6} + 4.00 \times 10^{5}\; m)} = -2.65 \times 10^{11}\; J \ldotp \end{split}\]
L'énergie totale à la surface de la Terre est
\[\begin{split} E_{surface} & = K_{surface} + U_{surface} = 0 - \frac{GmM_{E}}{r} \\ & = - \frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(9000\; kg)(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6}\; m)} \\ & = -5.63 \times 10^{11}\; J \ldotp \end{split}\]
Le changement d'énergie est
\[\Delta E = E_{orbit}− E_{surface} = 2.98 x 10^{11}\, J. \nonumber\]
Pour obtenir l'énergie cinétique, nous soustrayons le changement d'énergie potentielle de l'exemple 13.4.1,\(\Delta\) U = 3,32 x 10 10 J. Cela nous donne l'orbite K = (2,98 x 10 11) − (3,32 x 10 10) = 2,65 x 10 11 J. Comme indiqué précédemment, l'énergie cinétique d'une orbite circulaire représente toujours la moitié de l'amplitude de l'énergie potentielle et la même que la magnitude de l'énergie totale. Notre résultat le confirme.
La deuxième approche consiste à utiliser l'équation \ ref {13.7} pour déterminer la vitesse orbitale du Soyouz, ce que nous avons fait pour l'ISS dans l'exemple\(\PageIndex{1}\).
\[ \begin{align*} v_{orbit} &= \sqrt{\frac{GM_{E}}{r}} \\[4pt]&= \sqrt{\frac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(5.96 \times 10^{24}\; kg)}{(6.36 \times 10^{6} + 4.00 \times 10^{5})\; m}} \\[4pt] &= 7.67 \times 10^{3}\; m/s \end{align*}\]
Donc, l'énergie cinétique du Soyouz en orbite est
\[ \begin{align*}K_{orbit} &= \frac{1}{2} mv_{orbit}^{2} \\[4pt]&= \frac{1}{2} (9000\; kg)(7.67 \times 10^{3}\; m/s)^{2} \\[4pt]&= 2.65 \times 10^{11}\; J,\end{align*}\]
comme dans la méthode précédente. L'énergie totale est juste
\[ \begin{align*}E_{orbit} &= K_{orbit} + \Delta U \\[4pt]&= (2.65 \times 10^{11}) + (3.32 \times 10^{10}) \\[4pt]&= 2.95 \times 10^{11}\; J \ldotp\end{align*}\]
L'importance
L'énergie cinétique du Soyouz est presque huit fois supérieure à la variation de son énergie potentielle, soit 90 % de l'énergie totale nécessaire pour le rendez-vous avec l'ISS. Et il est important de se rappeler que cette énergie ne représente que l'énergie qui doit être donnée au Soyouz. Avec notre technologie de fusée actuelle, la masse du système de propulsion (le carburant de la fusée, son contenant et son système de combustion) dépasse de loin celle de la charge utile, et une énorme quantité d'énergie cinétique doit être affectée à cette masse. Le coût réel de l'énergie est donc plusieurs fois supérieur à celui du changement d'énergie de la charge utile elle-même.


