13.6 : Les lois du mouvement planétaire de Kepler
- Page ID
- 191323
- Décrire les sections coniques et leur relation avec le mouvement orbital
- Décrire comment la vitesse orbitale est liée à la conservation du moment cinétique
- Déterminer la période d'une orbite elliptique à partir de son axe principal
À l'aide des données précises collectées par Tycho Brahe, Johannes Kepler a soigneusement analysé les positions dans le ciel de toutes les planètes connues et de la Lune, en traçant leurs positions à intervalles de temps réguliers. À partir de cette analyse, il a formulé trois lois, que nous aborderons dans cette section.
La première loi de Kepler
L'opinion dominante à l'époque de Kepler était que toutes les orbites planétaires étaient circulaires. Les données relatives à Mars ont posé le plus grand défi à ce point de vue, ce qui a finalement incité Kepler à abandonner l'idée populaire. La première loi de Kepler stipule que chaque planète se déplace le long d'une ellipse, le Soleil étant situé au centre de l'ellipse. Une ellipse est définie comme l'ensemble de tous les points de telle sorte que la somme de la distance entre chaque point et deux foyers soit une constante. La figure\(\PageIndex{1}\) montre une ellipse et décrit une méthode simple pour la créer.
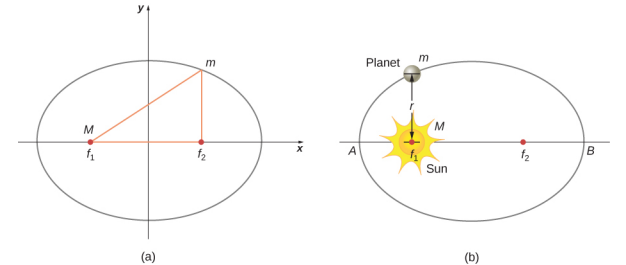
Pour les orbites elliptiques, le point d'approche le plus proche d'une planète par rapport au Soleil est appelé périhélie. Il est étiqueté point A sur la figure\(\PageIndex{1}\). Le point le plus éloigné est l'aphélie et est étiqueté point B sur la figure. Pour l'orbite de la Lune autour de la Terre, ces points sont appelés périgée et apogée, respectivement.
Une ellipse a plusieurs formes mathématiques, mais elles constituent toutes un cas spécifique de l'équation plus générale pour les sections coniques. Il existe quatre sections coniques différentes, toutes données par l'équation
\[\frac{\alpha}{r} = 1 + e \cos \theta \ldotp \label{13.10}\]
Les variables\(r\) et\(\theta\) sont illustrées sur la figure\(\PageIndex{2}\) dans le cas d'une ellipse. Les constantes α et e sont déterminées par l'énergie totale et le moment cinétique du satellite en un point donné. La constante e est appelée excentricité. Les valeurs de\(\alpha\) et e déterminent laquelle des quatre sections coniques représente la trajectoire du satellite.
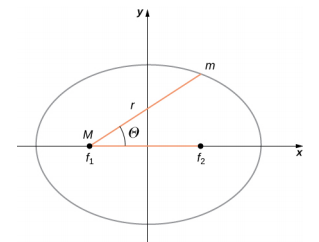
L'un des véritables triomphes de la loi de Newton sur la gravitation universelle, dont la force est proportionnelle à l'inverse de la distance au carré, est que lorsqu'elle est combinée à sa deuxième loi, la solution pour la trajectoire de tout satellite est une section conique. Chaque trajectoire empruntée par m est l'une des quatre sections coniques : un cercle ou une ellipse pour les orbites liées ou fermées, ou une parabole ou une hyperbole pour les orbites ouvertes ou illimitées. Ces sections coniques sont illustrées sur la figure\(\PageIndex{3}\).
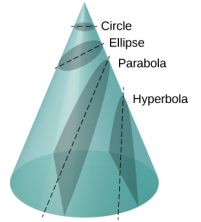
Si l'énergie totale est négative, alors 0 ≤ e < 1, et l'équation \ ref {13.10} représente une orbite bornée ou fermée d'une ellipse ou d'un cercle, où e = 0. [Vous pouvez voir dans l'équation 13.10 que pour e = 0, r =\(\alpha\), et donc le rayon est constant.] Pour les ellipses, l'excentricité est liée à l'aspect oblong de l'ellipse. Un cercle a une excentricité nulle, alors qu'une très longue ellipse allongée a une excentricité proche de une.
Si l'énergie totale est exactement nulle, alors e = 1 et le trajet est une parabole. Rappelons qu'un satellite dont l'énergie totale est nulle a exactement la même vitesse d'échappement. (La parabole est formée uniquement en tranchant le cône parallèlement à la tangente le long de la surface.) Enfin, si l'énergie totale est positive, alors e > 1 et le chemin est une hyperbole. Ces deux dernières trajectoires représentent des orbites illimitées, où m passe par M une fois et une seule fois. Cette situation a été observée pour plusieurs comètes qui s'approchent du Soleil puis s'éloignent pour ne jamais revenir.
Nous nous sommes limités au cas où la plus petite masse (planète) tourne autour d'une masse beaucoup plus grande, et donc stationnaire, (Soleil), mais l'équation 13.10 s'applique également à deux masses en interaction gravitationnelle. Chaque masse trace exactement la même section conique que l'autre. Cette forme est déterminée par l'énergie totale et le moment cinétique du système, le centre de gravité du système étant situé au centre de gravité du système. Le rapport des dimensions des deux trajectoires est l'inverse du rapport de leurs masses.
Vous pouvez voir une animation de deux objets en interaction sur la page Mon système solaire de PhET. Choisissez l'option de préréglage Soleil et planète. Vous pouvez également consulter les problèmes corporels multiples les plus complexes. Vous pouvez trouver la trajectoire réelle de la Lune assez surprenante, tout en obéissant aux lois simples du mouvement de Newton.
Transferts orbitaux
Les gens ont imaginé voyager vers les autres planètes de notre système solaire depuis leur découverte. Mais comment pouvons-nous le faire au mieux ? La méthode la plus efficace a été découverte en 1925 par Walter Hohmann, inspiré par un roman de science-fiction populaire de l'époque. La méthode est désormais appelée transfert de Hohmann. Dans le cas d'un déplacement entre deux orbites circulaires, le transfert se fait le long d'une ellipse « de transfert » qui intercepte parfaitement ces orbites au niveau de l'aphélie et du périhélie de l'ellipse. La figure\(\PageIndex{4}\) montre le cas d'un voyage entre l'orbite de la Terre et celle de Mars. Comme précédemment, le Soleil est au centre de l'ellipse.
Pour toute ellipse, le demi-grand axe est défini comme la moitié de la somme du périhélie et de l'aphélie. Dans la figure\(\PageIndex{4}\), le demi-grand axe est la distance entre l'origine et chaque côté de l'ellipse le long de l'axe X, ou juste la moitié de l'axe le plus long (appelé axe principal). Ainsi, pour passer d'une orbite circulaire de rayon r 1 à une autre orbite circulaire de rayon r 2, l'aphélie de l'ellipse de transfert sera égale à la valeur de l'orbite la plus grande, tandis que le périhélie sera l'orbite la plus petite. Le demi-grand axe, noté a, est donc donné par\(a = \frac{1}{2} (r_{1} + r_{2})\).
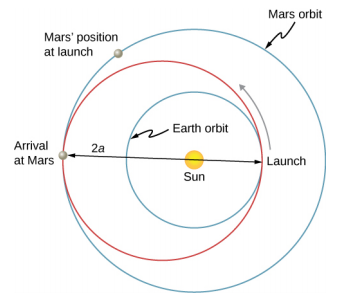
Prenons le cas d'un voyage de la Terre à Mars. Pour le moment, nous ignorons les planètes et supposons que nous sommes seuls sur l'orbite de la Terre et que nous souhaitons nous déplacer vers l'orbite de Mars. À partir de l'équation 13.9, l'expression de l'énergie totale, nous pouvons voir que l'énergie totale d'un vaisseau spatial sur la plus grande orbite (Mars) est supérieure (moins négative) à celle d'une orbite plus petite (Terre). Pour passer à l'ellipse de transfert depuis l'orbite de la Terre, nous devrons augmenter notre énergie cinétique, c'est-à-dire augmenter notre vitesse. La méthode la plus efficace consiste à accélérer très rapidement le long de la trajectoire orbitale circulaire, qui se trouve également le long de la trajectoire de l'ellipse à ce point. (En fait, l'accélération doit être instantanée, de telle sorte que les orbites circulaire et elliptique soient congruentes pendant l'accélération. En pratique, l'accélération finie est suffisamment courte pour que la différence ne soit pas un facteur significatif.) Une fois sur l'orbite de Mars, vous aurez besoin d'une nouvelle augmentation de vitesse pour vous déplacer sur cette orbite, ou vous resterez sur l'orbite elliptique et vous retournerez simplement au périhélie où vous avez commencé. Pour le trajet de retour, il vous suffit d'inverser le processus avec un rétro-boost à chaque point de transfert.
Pour passer à l'ellipse de transfert puis repartir, nous devons connaître la vitesse de chaque orbite circulaire et les vitesses orbitales de transfert au périhélie et à l'aphélie. L'augmentation de vitesse requise est simplement la différence entre la vitesse de l'orbite circulaire et la vitesse de l'orbite elliptique en chaque point. Nous pouvons trouver les vitesses orbitales circulaires à l'aide de l'équation 13.7. Pour déterminer les vitesses de l'ellipse, nous affirmons sans preuve (car cela dépasse le cadre de ce cours) que l'énergie totale d'une orbite elliptique est
\[E = - \frac{GmM_{S}}{2a}\]
où M S est la masse du Soleil et a est le demi-grand axe. Fait remarquable, c'est la même chose que l'équation 13.9 pour les orbites circulaires, mais la valeur du demi-grand axe remplace le rayon de l'orbite. Comme nous connaissons l'énergie potentielle à partir de l'équation 13.4, nous pouvons déterminer l'énergie cinétique et donc la vitesse nécessaires pour chaque point de l'ellipse. Nous laissons le défi de trouver ces vitesses de transfert pour un voyage de la Terre vers Mars.
Nous terminons cette discussion en soulignant quelques détails importants. Tout d'abord, nous n'avons pas pris en compte l'énergie potentielle gravitationnelle due à la Terre et à Mars, ni la mécanique de l'atterrissage sur Mars. Dans la pratique, cela doit faire partie des calculs. Deuxièmement, le timing est primordial. Vous ne voulez pas arriver sur l'orbite de Mars pour découvrir qu'elle n'y est pas. Nous devons quitter la Terre exactement au bon moment pour que Mars se trouve à l'aphélie de notre ellipse de transfert dès notre arrivée. Cette opportunité se présente tous les deux ans. Et le retour nécessite également un timing correct. Le voyage total prendrait un peu moins de 3 ans ! Il existe d'autres options qui permettent un transit plus rapide, notamment un survol de Vénus par assistance gravitationnelle. Mais ces autres options s'accompagnent d'un coût énergétique supplémentaire et d'un danger pour les astronautes.
Visitez ce site (https://openstaxcollege.org/l/21plantripmars) pour plus de détails sur la planification d'un voyage sur Mars.
Deuxième loi de Kepler
La deuxième loi de Kepler stipule qu'une planète balaie des zones égales en des temps égaux, c'est-à-dire que la zone divisée par le temps, appelée vitesse surfacique, est constante. Considérez Figure\(\PageIndex{5}\). Le temps qu'il faut à une planète pour se déplacer de la position A à la position B, balayant la zone A 1, est exactement le temps qu'il faut pour passer de la position C à D, balayer la zone A 2, et pour se déplacer de E à F, balayant la zone A 3. Ces zones sont les mêmes : A 1 = A 2 = A 3.
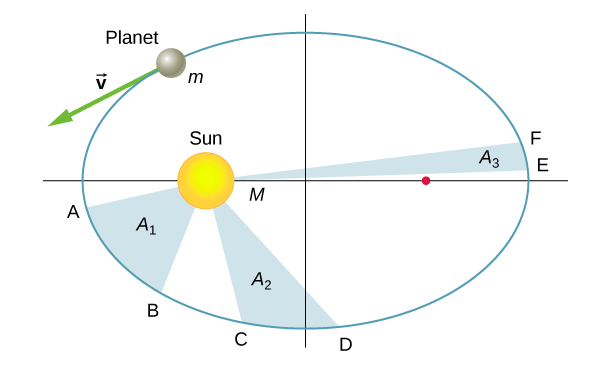
En comparant les zones de la figure et la distance parcourue le long de l'ellipse dans chaque cas, nous pouvons voir que pour que les surfaces soient égales, la planète doit accélérer à mesure qu'elle se rapproche du Soleil et ralentir à mesure qu'elle s'éloigne. Ce comportement est parfaitement conforme à notre équation de conservation, Equation \ ref {13.5}. Mais nous allons montrer que la deuxième loi de Kepler est en fait une conséquence de la conservation du moment cinétique, qui vaut pour tout système utilisant uniquement des forces radiales.
Rappelons la définition du moment cinétique à partir du moment cinétique,\(\vec{L} = \vec{r} \times \vec{p}\). Dans le cas du mouvement orbital,\(\vec{L}\) est le moment cinétique de la planète autour du Soleil,\(\vec{r}\) est le vecteur de position de la planète mesuré à partir du Soleil et\(\vec{p}\) = m\(\vec{v}\) est le moment linéaire instantané en tout point de l'orbite. Puisque la planète se déplace le long de l'ellipse, elle\(\vec{p}\) est toujours tangente à l'ellipse.
Nous pouvons diviser le moment linéaire en deux composantes : une composante radiale\(\vec{p}_{rad}\) le long de la ligne menant au Soleil et une composante\(\vec{p}_{perp}\) perpendiculaire à\(\vec{r}\). Le produit croisé du moment cinétique peut alors être écrit comme
\[\begin{align*} \vec{L} &= \vec{r} \times \vec{p} \\[4pt] &= \vec{r} \times (\vec{p}_{rad} + \vec{p}_{perp}) \\[4pt] &= \vec{r} \times \vec{p}_{rad} + \vec{r} \times \vec{p}_{perp} \ldotp \end{align*}\]
Le premier terme de droite est zéro car il\(\vec{r}\) est parallèle à et\(\vec{p}_{rad}\), dans le second terme,\(\vec{r}\) il est perpendiculaire à\(\vec{p}_{perp}\), de sorte que l'amplitude du produit croisé se réduit à
\[L = rp_{perp} = rmv_{perp}.\]
Notez que le moment cinétique ne dépend pas de\(p_{rad}\). Comme la force gravitationnelle est uniquement dans la direction radiale, elle peut uniquement changer\(p_{rad}\) et non\(p_{perp}\) ; par conséquent, le moment cinétique doit rester constant.
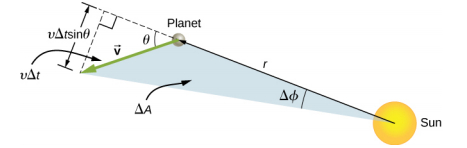
Maintenant, considérez Figure\(\PageIndex{6}\). Une petite zone triangulaire\(\Delta A\) est balayée dans le temps\(\Delta t\). La vitesse se situe le long de la trajectoire et forme un angle\(\theta\) avec la direction radiale. Par conséquent, la vitesse perpendiculaire est donnée par\(v_{perp}= v\sin \theta\). La planète se déplace d'une distance\(\Delta\) s = v\(\Delta\) tsin\(\theta\) projetée le long de la direction perpendiculaire à\(r\). Puisque l'aire d'un triangle est égale à la moitié de la base (\(r\)) multipliée par la hauteur (\(\Delta s\)), pour un petit déplacement, l'aire est donnée par
\[\Delta A = \frac{1}{2} r \Delta s. \nonumber\]
En substituant\(\Delta s\),\(m\) en multipliant par le numérateur et le dénominateur, et en réorganisant, nous obtenons
\[\Delta A = \frac{1}{2} r \Delta s = \frac{1}{2} r (v \Delta t \sin \theta) = \frac{1}{2m} r (mv \sin \theta \Delta t) = \frac{1}{2m} r (mv_{perp} \Delta t) = \frac{L}{2m} \Delta t \ldotp\]
La vitesse surfacique est simplement le taux de variation de la surface avec le temps, donc nous avons
\[ \text{areal velocity} = \frac{\Delta A}{\Delta t} = \frac{L}{2m} \ldotp\]
Le moment cinétique étant constant, la vitesse surfacique doit également être constante. C'est exactement la deuxième loi de Kepler. Comme pour la première loi de Kepler, Newton a montré qu'il s'agissait d'une conséquence naturelle de sa loi de gravitation.
Vous pouvez visionner une version animée de Figure\(\PageIndex{6}\), ainsi que de nombreuses autres animations intéressantes, sur le site de la School of Physics (University of New South Wales).
Troisième loi de Kepler
La troisième loi de Kepler indique que le carré de la période est proportionnel au cube du demi-grand axe de l'orbite. Dans Satellite Orbits and Energy, nous avons dérivé la troisième loi de Kepler pour le cas particulier d'une orbite circulaire. L'équation \ ref {13.8} nous donne la période d'une orbite circulaire de rayon r autour de la Terre :
\[T = 2 \pi \sqrt{\frac{r^{3}}{GM_{E}}} \ldotp \label{13.5.5}\]
Pour une ellipse, rappelons que le demi-grand axe est la moitié de la somme du périhélie et de l'aphélie. Pour une orbite circulaire, le demi-grand axe (\(a\)) est identique au rayon de l'orbite. En fait, l'équation \ ref {13.5.5} nous donne la troisième loi de Kepler si nous la\(r\) remplaçons simplement par\(a\) et mettons au carré les deux côtés.
\[T^{2} = \frac{4 \pi^{2}}{GM} a^{3} \label{13.11}\]
Nous avons modifié la masse de la Terre en une masse plus générale\(M\), puisque cette équation s'applique aux satellites orbitant autour de n'importe quelle masse importante.
Déterminez le demi-grand axe de l'orbite de la comète de Halley, étant donné qu'elle arrive au périhélie tous les 75,3 ans. Si le périhélie est de 0,586 UA, qu'est-ce que l'aphélie ?
Stratégie
On nous donne la période, de sorte que nous pouvons réorganiser l'équation \ ref {13.11}, en résolvant pour le demi-grand axe. Comme nous connaissons la valeur du périhélie, nous pouvons utiliser la définition du demi-grand axe, donnée plus haut dans cette section, pour trouver l'aphélie. Nous notons que 1 unité astronomique (UA) est le rayon moyen de l'orbite de la Terre et qu'elle est définie comme étant 1 UA = 1,50 x 10 11 m.
Solution
En réorganisant l'équation \ ref {13.11} et en insérant les valeurs de la période de la comète de Halley et de la masse du Soleil, nous avons
\[\begin{split} a & = \left(\dfrac{GM}{4 \pi^{2}} T^{2}\right)^{1/3} \\ & = \left(\dfrac{(6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2})(2.00 \times 10^{30}\; kg)}{4 \pi^{2}} (75.3\; yr \times 365\; days/yr \times 24\; hr/day \times 3600\; s/hr)^{2}\right)^{1/3} \ldotp \end{split}\]
Cela donne une valeur de 2,67 x 10 12 m ou 17,8 UA pour le demi-grand axe. Le demi-grand axe est la moitié de la somme de l'aphélie et du périhélie, donc nous avons
\[\begin{split} a & = \frac{1}{2} (aphelion + perihelion) \\ aphelion & = 2a - perihelion \ldotp \end{split}\]
En substituant les valeurs, nous avons trouvé que pour le demi-grand axe et la valeur donnée pour le périhélie, nous trouvons que la valeur de l'aphélie est de 35,0 UA.
L'importance
Edmond Halley, un contemporain de Newton, a d'abord soupçonné que trois comètes, signalées en 1531, 1607 et 1682, étaient en fait la même comète. Avant que Tycho Brahe ne mesure les comètes, on pensait qu'il s'agissait d'événements ponctuels, peut-être de perturbations de l'atmosphère, et qu'elles n'étaient pas affectées par le Soleil. Halley a utilisé la nouvelle mécanique de Newton pour prédire le retour de la comète homonyme en 1758.
L'orbite presque circulaire de Saturne a un rayon moyen d'environ 9,5 UA et a une période de 30 ans, tandis qu'Uranus a une moyenne d'environ 19 UA et une période de 84 ans. Est-ce que cela correspond à nos résultats pour la comète de Halley ?


