13.7 : Forces marémotrices

Objectifs d'apprentissage

• Expliquer l'origine des marées océaniques de la Terre
• Décrivez en quoi les marées douces et les marées sauteuses diffèrent
• Décrire comment les forces de marée affectent les systèmes binaires

L'origine des marées océaniques de la Terre fait l'objet de recherches continues depuis plus de 2000 ans. Mais les travaux de Newton sont considérés comme le début d'une véritable compréhension du phénomène. Les marées océaniques sont le résultat des forces de marée gravitationnelles. Ces mêmes forces de marée sont présentes dans n'importe quel corps astronomique. Ils sont responsables de la chaleur interne qui crée l'activité volcanique sur Io, l'une des lunes de Jupiter, et de la désintégration des étoiles trop proches des trous noirs.

Marées lunaires

Si vous vivez au bord de l'océan presque n'importe où dans le monde, vous pouvez observer la montée et la baisse du niveau de la mer environ deux fois par jour. Cela est dû à la combinaison de la rotation de la Terre autour de son axe et de l'attraction gravitationnelle de la Lune et du Soleil.

Examinons d'abord l'effet de la Lune. Dans la figure\(\PageIndex{1}\), nous regardons « vers le bas » le pôle Nord de la Terre. Un côté de la Terre est plus proche de la Lune que l'autre, d'une distance égale au diamètre de la Terre. La force gravitationnelle est donc plus grande du côté le plus proche que du côté éloigné. La magnitude au centre de la Terre se situe entre ces valeurs. C'est pourquoi un renflement de marée apparaît des deux côtés de la Terre.

Figure\(\PageIndex{1}\) : La force des marées étire la Terre le long de la ligne entre la Terre et la Lune. C'est la différence entre la force gravitationnelle de l'autre côté et celle du côté le plus proche qui crée le renflement de marée des deux côtés de la planète. Les variations des marées des océans sont de l'ordre de quelques mètres ; ce diagramme est donc très exagéré.

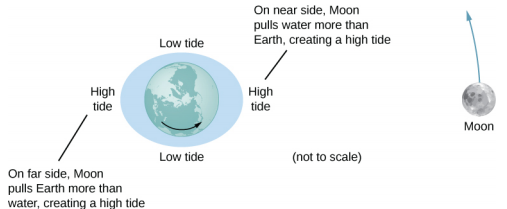
La force nette exercée sur la Terre l'amène à orbiter autour du centre de gravité Terre-Lune, situé à environ 1600 km sous la surface de la Terre, le long de la ligne entre la Terre et la Lune. La force de marée peut être considérée comme la différence entre la force au centre de la Terre et celle exercée à tout autre endroit. Sur la figure\(\PageIndex{2}\), cette différence est montrée au niveau de la mer, où nous observons les marées océaniques. (Notez que la variation du niveau de la mer provoquée par ces forces de marée est mesurée à partir du niveau de base de la mer. Nous avons vu plus tôt que la Terre se gonfle de plusieurs kilomètres à l'équateur en raison de sa rotation. Cela définit le niveau de base de la mer et nous ne prenons ici en compte que le renflement de marée beaucoup plus petit mesuré à partir de ce niveau de base de la mer.)

Figure\(\PageIndex{2}\) : La force de marée est la différence entre la force gravitationnelle au centre et celle qui se trouve ailleurs. Sur cette figure, les forces de marée sont représentées à la surface de l'océan. Ces forces diminueraient jusqu'à zéro à mesure que vous vous rapprochiez du centre de la Terre.

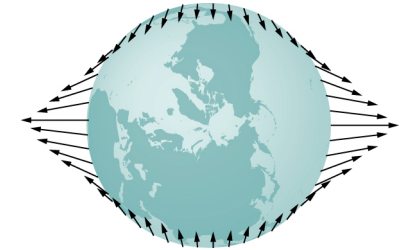
Pourquoi la montée et la descente des marées se produisent-elles deux fois par jour ? Regardez à nouveau Figure\(\PageIndex{1}\). Si la Terre ne tournait pas et que la Lune était fixe, les renflements resteraient au même endroit sur Terre. Par rapport à la Lune, les renflements restent fixes, le long de la ligne reliant la Terre à la Lune. Mais la Terre tourne (dans le sens indiqué par la flèche bleue) environ toutes les 24 heures. En 6 heures, les positions proches et lointaines de la Terre se déplacent vers l'endroit où se produisent les marées basses, et 6 heures plus tard, ces positions reprennent leur position de marée haute. Comme la Lune tourne également autour de la Terre environ tous les 28 jours, et dans le même sens que la Terre tourne, le temps entre les marées hautes (et basses) est en fait d'environ 12,5 heures. Le moment exact des marées est compliqué par de nombreux facteurs, dont le plus important est un autre corps astronomique : le Soleil.

L'effet du soleil sur les marées

Outre les forces de marée de la Lune sur les océans de la Terre, le Soleil exerce également une force de marée. L'attraction gravitationnelle du Soleil sur n'importe quel objet de la Terre est presque 200 fois supérieure à celle de la Lune. Cependant, comme nous le montrerons plus loin dans un exemple, l'effet de marée du Soleil est moindre que celui de la Lune, mais il n'en reste pas moins significatif. En fonction de la position de la Lune et du Soleil par rapport à la Terre, l'effet de marée net peut être amplifié ou atténué.

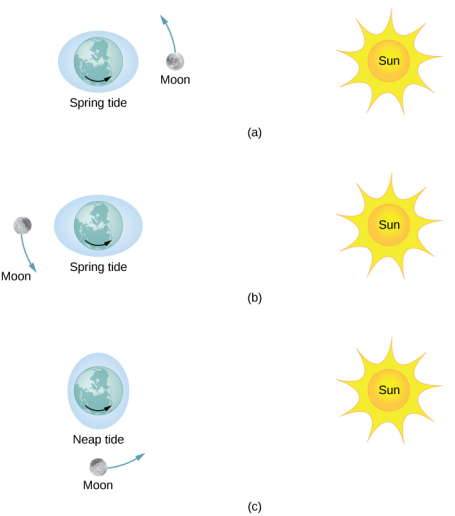
La figure\(\PageIndex{1}\) illustre les positions relatives du Soleil et de la Lune qui créent les plus grandes marées, appelées marées printanières (ou marées sauteuses). Pendant les marées de printemps, la Terre, la Lune et le Soleil sont alignés et les effets de marée s'ajoutent. (Rappelez-vous que les forces des marées provoquent des renflements des deux côtés.) La figure\(\PageIndex{1c}\) montre les positions relatives des plus petites marées, appelées marées basses. Les extrêmes des marées hautes et basses sont affectés. Les marées de printemps se produisent pendant la nouvelle lune ou la pleine lune, et les marées basses se produisent à la demi-lune.

Simulation

Vous pouvez voir une ou deux animations des marées en mouvement.

Figure\(\PageIndex{3}\) : (a et b) Les marées de printemps se produisent lorsque le Soleil et la Lune sont alignés, tandis que (c) les marées basses se produisent lorsque le Soleil et la Lune forment un triangle droit avec la Terre. (La figure n'est pas dessinée à l'échelle.)

L'ampleur des marées

Grâce à des données précises sur les positions de la Lune et du Soleil, il est possible de prévoir avec précision l'heure des marées maximales et minimales à la plupart des endroits de notre planète.

Visitez ce site pour générer des prévisions de marées pour une période allant jusqu'à 2 ans dans le passé ou dans le futur, dans plus de 3 000 sites aux États-Unis.

L'ampleur des marées est cependant bien plus complexe. Les angles relatifs de la Terre et de la Lune déterminent les marées de printemps et de marée basse, mais l'amplitude de ces marées dépend également de la distance par rapport à la Terre. Les forces de marée sont plus fortes lorsque les distances sont plus petites. L'orbite de la Lune autour de la Terre et celle de la Terre autour du Soleil sont elliptiques, de sorte qu'une marée printanière est exceptionnellement grande si elle se produit lorsque la Lune est au périgée et que la Terre est au périhélie. À l'inverse, elle est relativement petite si elle se produit lorsque la Lune est à l'apogée et que la Terre est à l'aphélie.

Les principales causes de variation des marées sont la topographie du littoral local et la bathymétrie (le profil de la profondeur) du fond de l'océan. L'amplitude des marées due à ces effets est étonnante. Bien que les marées océaniques soient bien inférieures à un mètre dans de nombreux endroits du monde, celles de la baie de Fundy (Figure\(\PageIndex{4}\)), sur la côte est du Canada, peuvent atteindre 16,3 mètres.

Figure\(\PageIndex{4}\) : Bateaux dans la baie de Fundy à marée haute et à marée basse. Le changement du niveau de la mer deux fois par jour constitue un véritable défi pour l'amarrage sûr des bateaux. (crédit : Dylan Kereluk)

Exemple\(\PageIndex{1}\): Comparing Tidal Forces

Comparez la force gravitationnelle de la Lune sur une masse de 1,0 kg située du côté proche et d'une autre de l'autre de l'autre côté de la Terre. Répétez l'opération pour le Soleil, puis comparez les résultats pour confirmer que les forces de marée de la Lune sont environ deux fois supérieures à celles du Soleil.

Stratégie

Nous utilisons la loi de la gravitation de Newton donnée par l'équation 13.2.1. Nous avons besoin des masses de la Lune et du Soleil et de leur distance par rapport à la Terre, ainsi que du rayon de la Terre. Nous utilisons les données astronomiques de l'annexe D.

Solution

En substituant la masse de la Lune et la distance moyenne entre la Terre et la Lune, nous avons

\[F_{12} = G \frac{m_{1} m_{2}}{r^{2}} = (6.67 \times 10^{-11}\; N\; \cdotp m^{2}/kg^{2}) \Bigg[ \frac{(1.0\; kg)(7.35 \times 10^{22}\; kg)}{(3.84 \times 10^{8} \pm 6.37 \times 10^{6}\; m)^{2}} \Bigg] \ldotp\]

Dans le dénominateur, nous utilisons le signe moins pour le côté proche et le signe plus pour le côté éloigné. Les résultats sont

\[F_{near} = 3.44 \times 10^{-5}\; N\; and\; F_{far} = 3.22 \times 10^{-5}\; N \ldotp\]

La force gravitationnelle de la Lune est presque 7 % plus élevée du côté proche de la Terre que de l'autre côté, mais les deux forces sont bien inférieures à celles de la Terre elle-même sur la masse de 1,0 kg. Néanmoins, cette petite différence est à l'origine des marées. Nous répétons maintenant le problème, en remplaçant la masse du Soleil par la distance moyenne entre la Terre et le Soleil. Les résultats sont

\[F_{near} = 5.89975 \times 10^{-3}\; N\; and\; F_{far} = 5.89874 \times 10^{-3}\; N \ldotp\]

Nous devons conserver six chiffres significatifs car nous voulons comparer la différence entre eux à la différence pour la Lune. (Bien que nous ne puissions pas justifier la valeur absolue avec cette précision, étant donné que toutes les valeurs du calcul sont identiques à l'exception des distances, la précision de la différence est toujours valide à trois chiffres.) La différence entre les forces proches et lointaines sur une masse de 1,0 kg dues à la Lune est

\[F_{near} = (3.44 \times 10^{-5}\; N) - (3.22 \times 10^{-5}\; N) = 0.22 \times 10^{-5}\; N,\]

alors que la différence pour le Soleil est

\[F_{near} - F_{far} = (5.89975 \times 10^{-3}\; N) - (5.89874 \times 10^{-3}\; N) = 0.101 \times 10^{-5}\; N \ldotp\]

Notez qu'une approche plus appropriée consiste à écrire la différence entre les deux forces en exprimant explicitement la différence entre les distances proches et lointaines. Avec juste un peu d'algèbre, nous pouvons montrer que

\[F_{tidal} = \frac{GMm}{r_{1}^{2}} - \frac{GMm}{r_{2}^{2}} = GMm \left(\dfrac{(r_{2} - r_{1})(r_{2} + r_{1})}{r_{1}^{2} r_{2}^{2}} \right) \ldotp\]

où r ₁ et r ₂ sont identiques à trois chiffres significatifs, mais leur différence (r ₂ − r ₁), égale au diamètre de la Terre, est également connue à trois chiffres significatifs. Les résultats du calcul sont les mêmes. Cette approche serait nécessaire si le nombre de chiffres significatifs nécessaires dépasse celui disponible sur votre calculatrice ou votre ordinateur.

L'importance

Notez que les forces exercées par le Soleil sont presque 200 fois supérieures aux forces exercées par la Lune. Mais la différence entre ces forces pour le Soleil est la moitié de celle pour la Lune. C'est la nature des forces de marée. La Lune a un effet de marée plus important parce que le changement fractionnaire de distance entre le côté le plus proche et le côté éloigné est beaucoup plus important pour la Lune que pour le Soleil.

exercice\(\PageIndex{1}\)

La Terre exerce une force de marée sur la Lune. Est-il supérieur, égal ou inférieur à celui de la Lune sur Terre ? Soyez prudent lorsque vous réagissez, car les forces de marée proviennent de la différence entre les forces gravitationnelles d'un côté et de l'autre. Examinez les calculs que nous avons effectués pour la force des marées sur Terre et considérez les valeurs qui changeraient de manière significative pour la Lune. Le diamètre de la Lune est le quart de celui de la Terre. Les forces de marée sur la Lune ne sont pas faciles à détecter, car il n'y a pas de liquide à la surface.

Autres effets de marée

Des forces de marée existent entre deux corps quelconques. L'effet étire les corps le long de la ligne entre leurs centres. Bien que l'effet des marées sur les mers de la Terre soit observable quotidiennement, les conséquences à long terme ne peuvent pas être observées aussi facilement. L'une des conséquences est la dissipation de l'énergie de rotation due au frottement lors de la flexion des corps eux-mêmes. La vitesse de rotation de la Terre ralentit à mesure que les forces des marées transfèrent l'énergie de rotation en chaleur. L'autre effet, lié à cette dissipation et à la conservation du moment cinétique, est appelé « verrouillage » ou synchronisation des marées. C'est déjà arrivé à la plupart des lunes de notre système solaire, y compris la Lune de la Terre. La Lune garde une face tournée vers la Terre ; sa vitesse de rotation est liée à la vitesse orbitale autour de la Terre. Le même processus se produit sur la Terre, et elle finira par garder une face tournée vers la Lune. Si cela se produit, nous ne verrons plus de marées, car le renflement des marées resterait au même endroit sur Terre et la moitié de la planète ne verrait jamais la Lune. Cependant, ce verrouillage prendra des milliards d'années, peut-être pas avant l'expiration de notre Soleil.

L'un des exemples les plus spectaculaires d'effets de marée se trouve sur Io, l'une des lunes de Jupiter. En 1979, la sonde Voyager a renvoyé des images spectaculaires de l'activité volcanique sur Io. C'est le seul autre corps astronomique de notre système solaire sur lequel nous avons observé une telle activité. La figure\(\PageIndex{5}\) montre une photo plus récente d'Io prise par le vaisseau spatial New Horizons alors qu'il se dirigeait vers Pluton, alors qu'il utilisait une assistance gravitationnelle de Jupiter.

Figure\(\PageIndex{5}\) : Des preuves spectaculaires des forces de marée peuvent être observées sur Io. L'éruption visible en bleu est due à la chaleur interne créée par les forces de marée exercées sur Io par Jupiter.

Pour certaines étoiles, l'effet des forces de marée peut être catastrophique. Les forces de marée dans des systèmes binaires très proches peuvent être suffisamment fortes pour arracher la matière d'une étoile à l'autre, une fois que les forces de marée dépassent les forces auto-gravitationnelles cohésives qui maintiennent les étoiles ensemble. Cet effet peut être observé dans les étoiles normales qui gravitent autour d'étoiles compactes voisines, telles que les étoiles à neutrons ou les trous noirs. La figure\(\PageIndex{6}\) montre l'interprétation de ce processus par un artiste. Lorsque la matière tombe dans l'étoile compacte, elle forme un disque d'accrétion qui devient surchauffé et rayonne dans le spectre des rayons X.

Figure\(\PageIndex{6}\) : Les forces de marée produites par un objet compact peuvent arracher de la matière à une étoile en orbite. Outre le disque d'accrétion qui orbite autour de l'objet compact, le matériau est souvent éjecté par des jets relativistes, comme illustré. (source : modification des travaux de l'Observatoire européen austral (ESO))

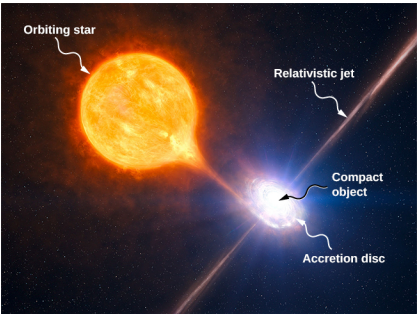
La production d'énergie de ces systèmes binaires peut dépasser la production typique de milliers d'étoiles. Un autre exemple pourrait être un quasar. Les quasars sont des objets très éloignés et extrêmement lumineux, qui dépassent souvent la production d'énergie de galaxies entières. Les astronomes s'accordent généralement à dire qu'il s'agit en fait d'énormes trous noirs qui produisent de l'énergie rayonnante lorsque de la matière arrachée par les marées aux étoiles voisines y tombe.