18.11 : Moment cinétique

Vérifiez votre compréhension

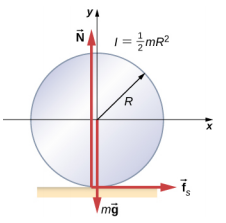
11.1. a.\(\mu_{S} \geq \frac{\tan \theta}{1 + \left(\dfrac{mr^{2}}{I_{CM}}\right)}\) ; en insérant l'angle et en notant que pour un cylindre creux I _CM = mr ², nous avons\(\mu_{S} \geq \frac{\tan 60^{o}}{1 + \left(\dfrac{mr^{2}}{mr^{2}}\right)} = \frac{1}{2} \tan 60^{o}\) = 0,87 ; on nous donne une valeur de 0,6 pour le coefficient de frottement statique, qui est inférieur à 0,87, de sorte que la condition n'est pas satisfaite et que le cylindre creux glissera ; b. un cylindre plein obéit à la condition\(\mu_{S} \geq \frac{1}{3} \tan \theta = \frac{1}{3} \tan 60^{o}\) = 0,58. La valeur de 0,6 pour\(\mu_{S}\) satisfait cette condition, de sorte que le cylindre plein ne glissera pas.

11.2. Sur la figure, nous voyons que le produit croisé entre le vecteur rayon et le vecteur moment donne un vecteur dirigé hors de la page. En insérant le rayon et le moment dans l'expression du moment cinétique, nous avons $$ \ vec {l} = \ vec {r} \ times \ vec {p} = (0,4 \ ; m \ ; \ hat {i}) \ times [1,67 \ times 10^ {−27} \ ; kg (4,0 \ times 10^ {6} \ ; m/s) \ hat {j}] = 2,7 \ fois 10^ −27} \ ; kg (4,0 \ times 10^ {6} \ ; m/s) \ hat {j}] = 2,7 \ fois 10^ {−27} \ ; kg 21} \ ; kg \ cdotp m^ {2} /s \ ; \ chapeau {k} \]

11.3. I _sphere =\(\frac{2}{5}\) mr ², I _cylinder =\(\frac{1}{2}\) mr ² ; En prenant le rapport des moments angulaires, nous avons :\(\frac{L_{cylinder}}{L_{sphere}} = \frac{I_{cylinder} \omega_{0}}{I_{sphere} \omega_{0}} = \frac{\frac{1}{2} mr^{2}}{\frac{2}{5} mr^{2}} = \frac{5}{4}\). Ainsi, le cylindre a 25 % de moment cinétique en plus. Cela est dû au fait que le cylindre a plus de masse répartie plus loin de l'axe de rotation.

11.4. En utilisant la conservation du moment cinétique, nous avons I (4,0 tr/min) = 1,25I\(\omega_{f}\),\(\omega_{f}\) =\(\frac{1.0}{1.25}\) (4,0 tr/min) = 3,2 tr/min

11,5. La gravité de la Lune est 1/6 de celle de la Terre. En examinant l'équation 11.12, nous constatons que la fréquence de précession du sommet est linéairement proportionnelle à l'accélération de la gravité. Toutes les autres quantités, la masse, le moment d'inertie et la vitesse de rotation sont les mêmes sur la Lune. Ainsi, la fréquence de précession sur la Lune est\(\omega_{P}\) (Lune) =\(\frac{1}{6} \omega_{P}\) (Terre) =\(\frac{1}{6}\) (5,0 rad/s) = 0,83 rad/s.

Questions conceptuelles

1. Non, la force de friction statique est nulle.

3. La roue est plus susceptible de glisser sur une pente abrupte, car le coefficient de frottement statique doit augmenter avec l'angle pour maintenir le mouvement de roulement sans glisser.

5. Le cylindre atteint une plus grande hauteur. Selon l'équation 11.20, son accélération dans la direction descendante de la pente serait moindre.

7. Tous les points de la ligne droite donneront un moment cinétique nul, car un vecteur croisé dans un vecteur parallèle est nul.

9. La particule doit se déplacer sur une ligne droite passant par l'origine choisie.

11. Sans la petite hélice, le corps de l'hélicoptère tournerait dans le sens inverse de celui de la grosse hélice afin de conserver le moment cinétique. La petite hélice exerce une poussée à une distance R du centre de masse de l'avion pour éviter que cela ne se produise.

13. La vitesse angulaire augmente car le moment d'inertie diminue.

15. Plus de masse est concentrée près de l'axe de rotation, ce qui diminue le moment d'inertie, ce qui fait augmenter la vitesse angulaire de l'étoile.

17. Un couple est nécessaire dans la direction perpendiculaire au vecteur de moment cinétique pour modifier sa direction. Ces forces s'exerçant sur le véhicule spatial sont extérieures au contenant dans lequel le gyroscope est monté et ne confèrent aucun couple au disque rotatif du gyroscope.

Des problèmes

19. v _CM = R\(\omega \Rightarrow \omega\) = 66,7 rad/s

21. \(\alpha\)= 3,3 rad/s ²

23. I _CM =\(\frac{2}{5}\) m ², _CM = 3,5 m/s ² ; x = 15,75 m

25. Le positif se trouve sur le plan incliné ; $$a_ {CM} = \ frac {mg \ sin \ theta} {m + \ left (\ dfrac {I_ {CM}} {r^ {2}} \ right)} \ Flèche droite I_ {CM} = r^ {2} \ Bigg [\ frac {mg \ sin 30} {a_ {CM}} − m \ Bigg], $$$x − x_ {0} = v_ {0} t − \ frac {1} {2} a_ {CM} t^ {2} \ Flèche droite a_ {CM} = 2,96 \ ; m/s^ {2}, $$$$I_ {CM} = 0,66 \ ; mr^ {2} \]

27. \(\alpha\)= 67,9 rad/s ², (un _centimètre) x = 1,5 m/s ²

29. W = −1080,0 M

31. L'énergie mécanique en bas est égale à l'énergie mécanique en haut ; $$ \ frac {1} {2} mv_ {0} ^ {2} + \ frac {1} {2} \ left (\ dfrac {1} {2} mr^ {2} \ right) \ left (\ dfrac {v_ {0}} {r} \ right) ^ {2} = mgh \ Flèche droite h = \ frac {1} {g} \ left (\ dfrac {1} {2} + \ dfrac {1} {4} \ right) v_ {0} ^ {2}, $$h = 7,7 m, donc la distance en haut de la pente est de 22 7,5 mm

33. Utilisez les économies d'énergie $$ \ begin {split} \ frac {1} {2} mv_ {0} ^ {2} + \ frac {1} {2} I_ {Cyl} \ omega_ {0} ^ {2} & = mgh_ {Cyl}, \ \ \ frac {1} {2} mv_ {0} ^ {2} + \ frac {1} {2} I_ {Sph} \ omega_ {0} ^ {2} & = mgh_ {Sph} \ ldotp \ end {split} $$En soustrayant les deux équations, en éliminant l'énergie de translation initiale, nous avons $$ \ frac { 1} {2} I_ {Cyl} \ omega_ {0} ^ {2} − \ frac {1} {2} I_ {Sph} \ omega_ {0} ^ {2} = mg (h_ {Cyl} − h_ {Sph}), $$$$ \ frac {1} {2} mr^ {2} \ gauche (\ dfrac {v_ {0}} {r} \ droite) ^ {2} − \ frac {1} {2} \ gauche (\ dfrac {2} {3} \ droite) mr^ {2} \ gauche (\ dfrac {v_ {0}} {r} \ droite) ^ {2} = mg (h_ {Cyl} − h_ {Sph}), $$$$ \ frac 1} {2} v_ {0} ^ {2} − \ frac {1} {2} \ left (\ dfrac {2} {3}} \ droite) v_ {0} ^ {2} = g (h_ {Cyl} − h_ {Sph}), $$$h_ {Cyl} − h_ {Sph} = \ frac {1} {g} \ gauche (\ dfrac {1} {2} − \ dfrac {1} {3} \ droite) v_ {0} ^ {2} = frac {1} {3} \ droite) v_ {0} ^ {2} = frac {1} {3} \ droite ac {1} {9.8 \ ; m/s^ {2}} \ left (\ dfrac {1} {6} \ right) (5,0 \ ; m/s) ^ {2} = 0,43 \ ; m \ LDotp$$Ainsi, la sphère creuse, avec le plus petit moment d'inertie, s'enroule jusqu'à une hauteur inférieure de 1,0 − 0. 43 = 0,57 m.

35. L'amplitude du produit croisé du rayon par rapport à l'oiseau et de son vecteur de moment donne rp sin\(\theta\), ce qui donne r sin\(\theta\) comme altitude de l'oiseau h. La direction du moment cinétique est perpendiculaire aux vecteurs rayon et moment, que nous choisissons arbitrairement comme suit\(\hat{k}\) : qui se trouve dans le plan du sol : $$ \ vec {L} = \ vec {r} \ times \ vec {p} = hmv \ ; \ hat {k} = (300,0 \ ; m) (2,0 \ ; kg) (20,0 \ ; m/s) \ ; \ hat {k} = 12 000,0 \ ; kg \ cdotp m^ {2} /s \ ; \ hat {k} \]

37. a.\(\vec{l}\) = 45,0 kg • m ² /s\(\hat{k}\)

b.\(\vec{\tau}\) = 10,0 N • m\(\hat{k}\)

39. a.\(\vec{l}_{1}\) = −0,4 kg • m ² /s\(\hat{k}\),\(\vec{l}_{2} = \vec{l}_{4}\) = 0,\(\vec{l}_{3}\) = 1,35 kg • m ² /s\(\hat{k}\)

b.\(\vec{L}\) = 0,95 kg • m ² /s\(\hat{k}\)

41. a. L = 1,0 x 10 ¹¹ kg • m ² /s

b. Non, le moment cinétique reste le même puisque le produit croisé ne concerne que la distance perpendiculaire entre le plan et le sol, quel que soit l'endroit où il se trouve le long de sa trajectoire.

43. un.\(\vec{v} = −gt\; \hat{j}, \vec{r}_{\perp} = −d;\ \hat{i}, \vec{l} = mdgt\; \hat{k}\)

b.\(\vec{F} = −mg\; \hat{j}, \Sigma \vec{\tau} = dmg\; \hat{k}\)

c. Oui

45. a. mgh =\(\frac{1}{2}\) m (r\(\omega\)) ² +\(\frac{1}{2} \left(\dfrac{2}{5}\right) mr^{2} \omega^{2}\) ;\(\omega\) = 51,2 rad/s ; L = 16,4 kg • m ² /s

b.\(\omega\) = 72,5 rad/s ; L = 23,2 kg • m ² /s

47. a. I = 720,0 kg • m ² ;\(\alpha\) = 4,20 rad/s ² ;\(\omega\) (10 s) = 42,0 rad/s ; L = 3,02 x 10 ⁴ kg • m ² /s ;\(\omega\) (20 s) = 84,0 rad/s

b.\(\tau\) = 3,03 x 10 ³ N • m

49. environ L = 1,131 x 10 ⁷ kg • m ² /s

b.\(\tau\) = 3,77 x 10 ⁴ N • m

51. \(\omega\)= 28,6 rad/s\(\Rightarrow\) L = 2,6 kg • m ² /s

53. $$L_ {f} = \ frac {2} {5} M_ {S} (3,5 \ fois 10^ {3} \ ; km) ^ {2} \ frac {2 \ pi} {T_ {f}}, $$$ (7,0 \ fois 10^ {5} \ ; km) ^ {2} \ frac {2 \ pi} {28 \ ; jours} = (3,5 \ fois 10^ {3} \ ; km) ^ {2} \ frac {2 \ pi} {T_ {f}} $$$T_ {f} \ Flèche droite = 28 \ ; jours \ frac {(3,5 \ fois 10^ {3} \ ; km) ^ {2}} {(7,0 \ fois 10^ {5}} \ ; km) ^ {2}} = 7,0 \ fois 10^ {2}} = 7,0 \ fois 10^ {2}} 4} \ ; jour = 60,5 \ ; s \]

55. f _f = 2,1 tr/min\(\Rightarrow\) f ₀ = 0,5 tr/min

57. r _P mv _P = r _A mv _A\(\Rightarrow\) v _P = 18,3 km/s

59. a. _Disque I = 5,0 x 10 ^-4 kg • m ², I _bug = 2,0 x 10 ^-4 kg • m ², (_disque I + I _bogue)\(\omega_{1}\) = _disque I\(\omega_{2}\),\(\omega_{2}\) = 14,0 rad/s

b.\(\Delta\) K = 0,014 J

c.\(\omega_{3}\) = 10,0 rad/s par rapport à la valeur initiale

d.\(\frac{1}{2}\) (_disque I + _bogue)\(\omega_{3}^{2}\) = 0,035 J pour revenir à la valeur d'origine

e. Fonctionnement de l'analyse des bogues sur le disque

61. L _i = 400,0 kg • m ² s, L _f = 500,0 kg • m ²\(\omega\),\(\omega\) = 0,80 rad/s

63. I ₀ = 340,48 kg • m ², I _f = 268,8 kg • m ²,\(\omega_{f}\) = 25,33 tr/min

65. a. L = 280 kg • m ² /s, I _f = 89,6 kg • m ²,\(\omega_{f}\) = 3,125 rad/s

b. K _i = 437,5 J, K _f = 437,5 J

67. Moment d'inertie lors du spin record : I ₀ = 0,5 kg • m ², I _f = 1,1 kg • m ²,\(\omega_{f} = \frac{I_{0}}{I_{f}} \omega_{0} \Rightarrow \) _{f f} = 155,5 tr/min

69. Sa vitesse de rotation dans l'air est la suivante : _{f f} = 2,0 tr/min ; elle peut faire quatre sauts en l'air.

71. Moment d'inertie lorsque tous les enfants sont à bord : I ₀ = 2,4 x 10 ⁵ kg • m ² ; I _f = 1,5 x 10 ⁵ kg • m ² ; _{f f} = 0,3 tr/min

73. I ₀ = 1,00 x 10 ¹⁰ kg • m ², I _f = 9,94 x 10 ⁹ kg • m ², _{f f} = 3,32 tr/min

75. I = 2,5 x 10 ⁻³ kg • m ²,\(\omega_{P}\) = 0,78 rad/s

77. a. L _Terre = 7,06 x 10 ³³ kg • m ² /s,\(\Delta\) L = 5,63 x 10 ³³ kg • m ² /s

b.\(\tau\) = 1,7 x 10 ²² N • m

c. Les deux forces à l'équateur auraient la même amplitude mais des directions différentes, l'une dans la direction nord et l'autre dans la direction sud sur le côté opposé de la Terre. L'angle entre les forces et les bras de levier par rapport au centre de la Terre est de 90°, donc un couple donné aurait une amplitude\(\tau\) = FR _E sin 90° = FR _E. Les deux fourniraient un couple dans le même sens :\(\tau\) = 2FR _E\(\Rightarrow\) F = 1,3 x 10 ¹⁵ N

Problèmes supplémentaires

79. a _CM = −\(\frac{3}{10}\) g, v ² = v ₀ ^{2 + 2} a _CM x\(\Rightarrow\) v ² = (7,0 m/s) ² − 2\(\left(\dfrac{3}{10}g\right)\) x, v ² = 0\(\Rightarrow\) x = 8,34 m

b. t =\(\frac{v − v_{0}}{a_{CM}}\), v = v ₀ + a _CM t\(\Rightarrow\) t = 2,38 s ; La sphère creuse a un moment d'inertie plus important et est donc plus difficile à immobiliser que le marbre ou la sphère pleine. La distance parcourue est plus grande et le temps écoulé est plus long.

8,1 a. W = −500,0 J

b. K + U _grav = constant, 500 J + 0 = 0 + (6,0 kg) (9,8 m/s ²) h, h = 8,5 m, d = 17,0 m ; le moment d'inertie étant moindre pour la sphère creuse, il faut donc moins de travail pour l'arrêter. De même, il enroule la pente sur une distance plus courte que le cerceau.

83. a.\(\tau\) = 34,0 N • m

b. l = mr ²\(\omega \Rightarrow \omega\) = 3,6 rad/s

85. a. d _M = 3,85 x 10 ⁸ m de distance moyenne par rapport à la Lune ; période orbitale 27,32d = 2,36 x 10 ⁶ s ; vitesse de la Lune\(\frac{2 \pi 3.85 \times 10^{8}\; m}{2.36 \times 10^{6}\; s}\) = 1,0 x 10 ³ m/s ; masse de la Lune 7,35 x 10 ²² kg, L = 2,90 x 10 ³⁴ kgm ² /s

b. Rayon de la Lune 1,74 x 10 ⁶ m ; la période orbitale est la même que (a) :\(\omega\) = 2,66 x 10 ⁻⁶ rad/s, L = 2,37 x 1029 kg • m ² /s ; Le moment cinétique orbital est 1,22 x 10 ⁵ fois plus grand que le moment cinétique de rotation de la Lune.

87. I = 0,135 kg • m ²,\(\alpha\) = 4,19 rad/s ²\(\omega = \omega_{0} + \alpha t\),\(\omega\) (5 s) = 21 rad/s, L = 2,84 kg • m ² /s,\(\omega\) (10 s) = 41,9 rad/s, L = 5,66 kg • m/s ²

89. Dans l'équation de conservation du moment cinétique, le taux de rotation apparaît des deux côtés. Nous conservons donc la notation (tr/min) car la vitesse angulaire peut être multipliée par une constante pour obtenir (tr/min) : L _i = −0,04 kg • m ² (300,0 tr/min), L _f = (0,08 kg • m ²) f _{f f\(\Rightarrow\) f} = −150,0 tr/min dans le sens des aiguilles d'une montre

91. I ₀\(\omega_{0}\) = I _f\(\omega_{f}\), I ₀ = 6 120,0 kg • m ², I _f = 1180,0 kg • m ²,\(\omega_{f}\) = 31,1 tr/min

93. L _i = 1,00 x 10 ⁷ kg • m ² /s, I _f = 2,025 x 10 ⁵ kg • m ²,\(\omega_{f}\) = 7,86 tr/min

Problèmes liés au défi

95. Supposons que le roulis s'accélère vers l'avant par rapport au sol avec une accélération a'. Il accélère ensuite vers l'arrière par rapport au camion avec une accélération (a − a′).

De plus, R\(\alpha\) = a − a′, I =\(\frac{1}{2}\) mR ²,\(\Sigma\) F _x = f _s = ma′,\(\Sigma \tau\) = f _s R = I\(\alpha\) = I = I\(\frac{a − a′}{R}\), f _s =\(\frac{I}{R^{2}}\) (a − a′) =\(\frac{1}{2}\) m (a − a′)

Résolution de a′ : f _s =\(\frac{1}{2}\) m (a − a′), a′ =\(\frac{a}{3}\), x − x ₀ = v ₀ t+\(\frac{1}{2}\) à ², d =\(\frac{1}{3}\) à ², t =\(\sqrt{\frac{3d}{a}}\), donc, s = 1,5d

97. a. La tension de la corde fournit la force centripète telle que T sin\(\theta\) = mr _\(\perp\)\(\omega^{2}\). La composante de la tension qui est verticale s'oppose à la force gravitationnelle de telle sorte que T cos\(\theta\) = mg. Cela donne T = 5,7 N. Nous résolvons pour r _\(\perp\)= 0,16 m. Cela donne la longueur de la corde comme r = 0,32 m. À\(\omega\) = 10,0 rad/s, il y a un nouvel angle, une nouvelle tension et un nouveau rayon perpendiculaire à la tige. En divisant les deux équations impliquant la tension pour l'éliminer, nous avons\(\frac{\sin \theta}{\cos \theta} = \frac{(0.32\; m\; \sin \theta) \omega^{2}}{g} \Rightarrow \frac{1}{\cos \theta} = \frac{(0.32\; m) \omega^{2}}{g}\) ; cos\(\theta\) = 0,31\(\Rightarrow \theta\) = 72,2°

b. l _initial = 0,08 kg • m ² /s, l _final = 0,46 kg• m ² /s

c. Non, le cosinus de l'angle est inversement proportionnel au carré de la vitesse angulaire, donc dans l'ordre de\(\theta\) → 90°,\(\omega\) → ∞. La canne devrait tourner à l'infini.

Contributeurs et attributions

Template:ContribOpenStaxUni