Skip to main content
Global

18.3 : Mouvement le long d'une ligne droite

  1. Last updated
  2. Save as PDF
  • Page ID
    191341

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Vérifiez votre compréhension

    3.1. (a) Le déplacement du cycliste est\(\Delta\) x = x f − x 0 = −1 km. (Le déplacement est négatif parce que nous prenons l'est pour être positif et l'ouest pour être négatif.) (b) La distance parcourue est de 3 km + 2 km = 5 km. (c) L'ampleur du déplacement est de 1 km.

    3.2. (a) En prenant la dérivée de x (t), on obtient v (t) = −6t m/s. (b) Non, car le temps ne peut jamais être négatif. (c) La vitesse est v (1,0 s) = −6 m/s et la vitesse est |v (1,0 s) | = 6 m/s.

    3.3. En insérant les connaissances, nous l'avons fait\(\bar{a} = \frac{\Delta v}{\Delta t} = \frac{2.0 \times 10^{7}\; m/s − 0}{10^{−4}\; s − 0} = 2.0 \times 10^{11}\; m/s^{2}\).

    3.4. Si nous prenons l'est pour être positif, alors l'avion a une accélération négative parce qu'il accélère vers l'ouest. Il décélère également ; son accélération est dans le sens opposé à sa vitesse.

    3.5. Pour répondre à cette question, choisissez une équation qui nous permet de résoudre pour le temps t, étant donné uniquement a, v 0 et v$$v = v_ {0} + at \ ldotp$$ Réorganiser pour résoudre pour t : $$t = \ frac {v − v_ {0}} {a} = \ frac {400 \ ; m/s − 0 \ ; m/s} {20 \ ; m/s^ {2}} = [20 \ \ \ \ \ \ \ \ \ \]

    3.6. a =\(\frac{2}{3}\) m/s 2

    3.7. Il faut 2,47 s pour atteindre l'eau. La distance parcourue augmente plus rapidement.

    3.8. a. La fonction de vitesse est l'intégrale de la fonction d'accélération plus une constante d'intégration. Par l'équation 3.91, $$v (t) = \ int a (t) dt + C_ {1} = \ int (5 − 10t) dt + C_ {1} = 5t − 5t^ {2} + C_ {1} \ ldotp$$ Puisque v (0) = 0, nous avons C 1 = 0 ; donc, $$v (t) = 5t − 5t^ {2} \ ldotp$$ b. Par l'équation 3,93, $$x (t) = \ int v (t) dt + C_ {2} = \ int (5t − 5t^ {2}) dt + C_ {2} = \ frac {5} {2} t^ {2} − \ frac {5} {3} t^ {3} + C_ {2} \ ldotp$$ Puisque x (0) = 0, nous avons C 2 = 0, et$$x (t) = \ frac {5} {2} t^ {2} − \ frac {5} {3} t^ {3} \ ldotp$$ c. La vélocité peut être écrite comme v (t) = 5t (1 — t), qui est égal à zéro à t = 0, et t = 1 s.

    Questions conceptuelles

    1. Vous conduisez votre voiture pour vous rendre en ville et revenez passer devant votre maison pour vous rendre chez un ami.

    3. Si les bactéries se déplacent d'avant en arrière, les déplacements s'annulent mutuellement et le déplacement final est faible.

    5. Distance parcourue

    7. La vitesse moyenne est la distance totale parcourue divisée par le temps écoulé. Si vous vous promenez, que vous quittez votre domicile et que vous y retournez, votre vitesse moyenne est un chiffre positif. Puisque Vélocité moyenne = Déplacement/Temps écoulé, votre vitesse moyenne est nulle.

    9. Vitesse moyenne Ils sont identiques si la voiture ne fait pas marche arrière.

    11. Non, dans une dimension, la vitesse constante ne nécessite aucune accélération.

    13. Une balle est projetée en l'air et sa vitesse est nulle au sommet du lancer, mais l'accélération n'est pas nulle.

    15. Plus, moins

    17. Si l'accélération, le temps et le déplacement sont connus et que les vitesses initiale et finale sont inconnues, alors deux équations cinématiques doivent être résolues simultanément. De plus, si la vitesse finale, le temps et le déplacement sont connus, deux équations cinématiques doivent être résolues pour la vitesse et l'accélération initiales.

    19. a. Au sommet de sa trajectoire ; b. oui, au sommet de sa trajectoire ; c. oui

    21. Terre$V = v_ {0} − gt = −gt ; $$ Lune$$v′ = \ frac {g} {6} t′$$ $v = v′ − gt = − \ frac {g} {6} t′$$ $t′ = 6t ; $$ Terre $$y = − \ frac {1} {2} gt^ {2} $$ Lune $$t′ = 6t ; $$ Terre $$y = − \ frac {1} {2} gt^ {2} $$ Lune $$t′ y′ = − \ frac {1} {2} \ frac {g} {6} (6t) ^ {2} = − \ frac {1} {2} g6t^ {2} = −6 \ left (\ dfrac {1} {2} gt^ {2} \ right) = −6y \]

    Problèmes

    25. a.\(\vec{x}_{1}\) = (−2,0 m)\(\hat{i}\),\(\vec{x}_{2}\) = (5,0 m)\(\hat{i}\)

    b. 7,0 km à l'est

    27. a. t = 2,0 s

    b. x (6,0) − x (3,0) = −8,0 − (−2,0) = −6,0 m

    29. environ 150,0 s,\(\vec{v}\) = 156,7 m/s

    b. 45,7 % de la vitesse du son au niveau de la mer

    31.

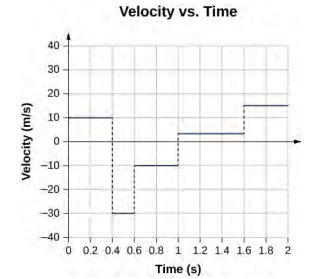
    Le graphique montre la vitesse en mètres par seconde tracée en fonction du temps en secondes. La vitesse commence à 10 mètres par seconde, diminue à -30 à 0,4 seconde ; augmente à -10 mètres à 0,6 seconde, augmente à 5 à 1 seconde, augmente à 15 à 1,6 seconde.

    33.

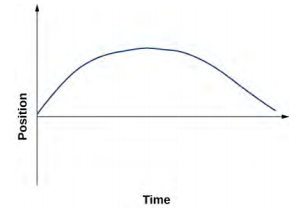
    Le graphique montre la position tracée en fonction du temps. Il commence à l'origine, augmente pour atteindre son maximum, puis diminue près de zéro.

    35. a. v (t) = (10 − 4 t) m/s ; v (2 s) = 2 m/s, v (3 s) = −2 m/s

    b. |v (2 s) | = 2 m/s, |v (3 s) | = 2 m/s

    c.\(\bar{v}\) = 0 m/s

    37. a = 4,29 m/s 2

    39.

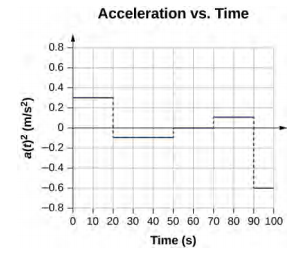
    Le graphique montre l'accélération en mètres par seconde au carré par rapport au temps en secondes. L'accélération est de 0,3 mètre par seconde au carré entre 0 et 20 secondes, de -0,1 mètre par seconde au carré entre 20 et 50 secondes, de zéro entre 50 et 70 secondes, de -0,6 entre 90 et 100 secondes.

    41. a = 11,1 g

    43. 150 m

    45. environ 525 m

    b. v = 180 m/s

    47. un.

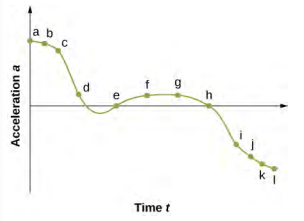
    Le graphique est un diagramme de l'accélération a en fonction du temps t. Le graphique est non linéaire, l'accélération étant positive au début, négative à la fin et traversant l'axe x entre les points d et e et les points e et h.

    b. L'accélération a la valeur positive la plus élevée à t a c. L'accélération est nulle à t e et t h d. L'accélération est négative à t i, t j, t k, t l

    49. a. a = −1,3 m/s 2

    b. v 0 = 18 m/s

    c. t = 13,8 s

    51. v = 502,20 m/s

    53. un.

    La figure montre un objet avec une vitesse égale à 0 mètre par seconde et une accélération égale à 2,4 mètres par seconde au carré au point zéro. Lorsque le temps est égal à 12 secondes, l'accélération reste égale à 2,4 mètres par seconde. La vitesse et la position de l'objet sont inconnues.

    b. Connus : a = 2,40 m/s 2, t = 12,0 s, v 0 = 0 m/s et x 0 = 0 m ; c. x = x 0 + v 0 t +\(\frac{1}{2}\) à 2 =\(\frac{1}{2}\) à 2 = 2,40 m/s 2 (12,0 s) 2 = 172,80 m, la réponse semble raisonnable à environ 172,8 m ; d. v = 28,8 m/s

    55. un.

    La figure montre un objet avec une vitesse nulle et une accélération inconnue au début. Après un temps inconnu, l'objet atteint une vitesse de 30 centimètres par seconde et se trouve à 1,8 cm du point de départ. L'accélération de l'objet à ce stade n'est pas connue.

    b. Connus : v = 30,0 cm/s, x = 1,80 cm

    c. a = 250 cm/s 2, t = 0,12 s

    d. Oui

    57. environ 6,87 m/s 2

    b. x = 52,26 m

    59. a. a = 8 450 m/s 2

    b. t = 0,0077 s

    61. a. a = 9,18 g

    b. t = 6,67 x 10 −3 s

    c. a = −40,0 m/s 2, a = 4,08 g

    63. Connues : x = 3 m, v = 0 m/s, v0 = 54 m/s. Nous voulons a, donc nous pouvons utiliser cette équation : a = −486 m/s 2.

    65. a. a = 32,58 m/s 2

    b. v = 161,85 m/s

    c. v > v max, car l'hypothèse d'une accélération constante n'est pas valable pour un dragster. Un dragster change de vitesse et aurait une accélération plus importante en première vitesse qu'en deuxième vitesse qu'en troisième vitesse, et ainsi de suite. L'accélération serait maximale au début, donc elle n'accélérerait pas à 32,6 m/s 2 au cours des derniers mètres, mais nettement moins, et la vitesse finale serait inférieure à 162 m/s.

    67. a. y = −8,23 m, v 1 = −18,9 m/s

    b. y = −18,9 m, v 2 = 23,8 m/s

    c. y = −32 m, v 3 = −28,7 m/s

    d. y = −47,6 m, v 4 = −33,6 m/s

    soit y = −65,6 m, v 5 = −38,5 m/s

    69. a. Connus : a = −9,8 m/s 2, v 0 = −1,4 m/s, t = 1,8 s, y 0 = 0 m

    b. y = y 0 + v 0 t −\(\frac{1}{2}\) gt 2, y = v 0 t −\(\frac{1}{2}\) gt = −1,4 m/s (1,8 sec) −\(\frac{1}{2}\) (9,8) (1,8 s) 2 = −18,4 m et l'origine se trouve chez les sauveteurs, qui se trouvent à 18,4 m au-dessus de l'eau.

    71. a. v 2 = v 0 2 − 2 g (y − y 0), y 0 = 0, v = 0, y\(\frac{v_{0}^{2}}{2g}\) =\(\frac{(4.0 m/s)^{2}}{2(9.80)}\) = 0,82 m

    b. Au sommet v = 0,41 s fois 2 à la planche = 0,82 s de la planche à l'eau y = y 0 + v 0 t −\(\frac{1}{2}\) gt 2, y = −1,80 m, y 0 = 0, v 0 = 4,0 m/s −1,8 = 4,0t − 4,9t 2, 4,9t 2 − 4,9t 2 − 4,0 t − 1,80 = 0, solution à l'équation quadratique donne 1,13 s

    c. v 2 = v 0 2 − 2 g (y − y 0) y 0 = 0, v 0 = 4,0 m/s, y = −1,80 m, v = 7,16 m/s

    73. Temps jusqu'au sommet : t = 1,12 s fois 2 équivaut à 2,24 s pour une hauteur de 2,20 m. Pour 1,80 m de hauteur, il faut ajouter 0,40 m. $$y = y_ {0} + v_ {0} t − \ frac {1} {2} gt^ {2} $$$$y = −0,40 \ ; m$$$$y_ {0} = 0$$$v$y = 0$$$v$y = −0,40 \ ; m$$$$y_ {0} = 0$$$v$y _ {0} = −11,0 \ ; m/s$$$$−0,40 = −11,0t − 4,9t^ {2} \ ; ou \ ; 4,9t^ {2} + 11,0t − 0,40 = 0 \ ldotp$$ Prenez la racine positive, le temps nécessaire pour parcourir 0,4 m supplémentaire est donc de 0,04 s. Le temps total est de 2,24 s + 0,04 s = 2,28 s.

    75. a. v 2 = v 0 2 − 2g (y − y 0), y 0 = 0, v = 0, y = 2,50 m, $$v_ {0} ^ {2} = 2gy \ Flèche droite v_ {0} = \ sqrt {2 (9,80) (2,50)} = 7,0 \ ; m/s ; \]

    b. t = 0,72 s fois 2 donne 1,44 s dans l'air

    77. a. v = 70,0 m/s

    b. temps entendu après que la roche a commencé à tomber : 0,75 s, temps pour atteindre le sol : 6,09 s

    79. a. A = m/s 2, B = m/s 5/2

    b. v (t) =\(\int\) a (t) dt + C 1 =\(\int\) (A − Bt 1/2) dt + C 1 = À −\(\frac{2}{3}\) Bt 3/2 + C 1\[v(0) = 0 = C_{1}\; so\; v(t_{0}) = At_{0} − \frac{2}{3} Bt_{0}^{3/2};\]

    c. x (t) =\(\int\) v (t) dt + C 2 =\(\int\) (At − \ frac {2} {3} \) Bt 3 /2) dt + C 2 =\(\frac{1}{2}\) À 2 −\(\frac{4}{15}\) Bt 5/2 + C 2\[x(0) = 0 = C_{2}\; so\; x(t_{0}) = \frac{1}{2} At_{0}^{2} − \frac{4}{15} Bt_{0}^{5/2}\]

    81. a. $$ \ begin {split} a (t) & = 3,2 m/s^ {2} \ quad t \ leq 5.0 \ ; s \ \ a (t) & = 1,5 \ ; m/s^ {2} \ quad 5.0 \ ; s \ leq t \ leq 11,0 \ ; s \ \ a (t) & = 0 \ ; m/s^ {2} \ quad \ quad t > 11,0 \ s ; \ end {split} \]

    b. $$ \ begin {split} x (t) & = \ int v (t) dt + C_ {2} = \ int 3,2 tdt + C_ {2} = 1,6 t^ {2} + C_ {2} \ quad t \ leq 5.0 \ ; s \ \ x (0) & = 0 \ Flèche droite C_ {2} = 0 \ ; donc, \ ; x (2,0 \ s) = 6,4 \ ; m \ \ x (t) & = \ int v (t) dt + C_ {2} = \ int [16,0 − 1,5 (t − 5,0)] dt + C_ {2} = 16 t − 1,5 \ gauche (\ dfrac {t^ {2}} {2}} {2} − 5,0 t \ droite) + C_ {2} \ quad 5.0 \ ; s \ leq t \ leq 11,0 \ ; s \ \ x (5 \ ; s) & = 1,6 (5,0) ^ {2} = 40 \ ; m = 16 (5,0 \ ; s) − 1,5 \ left (\ dfrac {5^ {2}}} {2} − 5,0 (5,0) \ right) + C_ {2} \ end {2}} (\ dfrac {5^ {2}}} {2}} {2} $$$ \ begin {split} 40 & = 98,75 + C_ {2} \ Flèche droite C_ {2} = −58,75 \ \ x (7,0 s) & = 16 (7,0) − 1,5 \ left (\ dfrac {7^ {2}}} {2} − 5,0 (7) \ right) − 58. 75 = 69 \ ; m \ \ x (t) & = \ int 7,0 dt + C_ {2} = 7 t + C_ {2} \ quad t \ geq 11,0 \ ; s \ \ x (11,0 \ ; s) & = 16 (11) − 1,5 \ left (\ dfrac {11^ {2}}} {2} − 5,0 (11) \ droite) − 58,75 = 109 7 (11,0 \ ; s) + C_ {2} \ Flèche droite C_ {2} = 32 \ ; m \ \ x (t) & = 7t + 32 \ ; m \ quad x \ geq 11,0 \ ; s \ Flèche droite x (12,0 \ ; s) = 7 (12) + 32 = 116 \ ; m \ end {divisé} \]

    Problèmes supplémentaires

    83. Tournez vers l'ouest dans la direction positive. 1er plan :\(\bar{v}\) = 600 km/h ; 2e plan :\(\bar{v}\) = 667,0 km/h

    85. a =\(\frac{v − v_{0}}{t − t_{0}}\), t = 0, a\(\frac{−3.4\; cm/s − v_{0}}{4\; s}\) = 1,2 cm/s 2\(\Rightarrow\) v 0 = − 8,2 cm/s, v = v 0 + at = − 8,2 + 1,2 t ; v = −7,0 cm/s, v = −1,0 cm/s

    87. a = −3 m/s 2

    89. a. v = 8,7 x 10 5 m/s

    b. t = 7,8 x 10 −8 s

    91. 1 km = v 0 (80,0 s) +\(\frac{1}{2}\) a (80,0) 2 ; 2 km = v 0 (200,0) +\(\frac{1}{2}\) a (200,0) 2 résolvez simultanément pour obtenir a =\(− \frac{0.1}{2400.0}\) km/s 2 et v 0 = 0,014167 km/s, soit 51,0 km/h. La vitesse à la fin du trajet est v = 21,0 km/h.

    93. a = −0,9 m/s 2

    95. Équation de la voiture en excès de vitesse : Cette voiture a une vitesse constante, qui est la vitesse moyenne, et n'accélère pas. Utilisez donc l'équation du déplacement avec x 0 = 0 : x = x 0 +\(\bar{v}\) t =\(\bar{v}\) t ; Équation pour la voiture de police : Cette voiture accélère, utilisez donc le équation du déplacement avec x 0 = 0 et v 0 = 0, puisque la voiture de police part de l'arrêt : x = x 0 + v 0 t +\(\frac{1}{2}\) à 2 =\(\frac{1}{2}\) à 2 ; Nous avons maintenant une équation de mouvement pour chaque voiture avec un paramètre commun, qui peut être éliminé pour trouver la solution. Dans ce cas, nous résolvons pour t. Étape 1, en éliminant x : x =\(\bar{v}\) t =\(\frac{1}{2}\) à 2 ; Étape 2, en résolvant pour t : t =\(\frac{2 \bar{v}}{a}\). La voiture en excès de vitesse a une vitesse constante de 40 m/s, qui est sa vitesse moyenne. L'accélération de la voiture de police est de 4 m/s 2. En évaluant t, le temps nécessaire à la voiture de police pour atteindre la voiture en excès de vitesse, nous avons t\(\frac{2 \bar{v}}{a}\)\(\frac{2(40)}{4}\) = = = 20 s.

    97. À cette accélération, elle s'arrête complètement en t = =\(\frac{−v_{0}}{a}\)\(\frac{8}{0.5}\) = 16 s, mais la distance parcourue est x = 8 m/s (16 s) −\(\frac{1}{2}\) (0,5) (16 s) 2 = 64 m, soit moins que la distance parcourue par rapport à la ligne d'arrivée, elle ne termine donc jamais la course.

    99. x 1 =\(\frac{3}{2}\) v 0 t ; x 2 =\(\frac{5}{3}\) x 1

    101. v 0 = 7,9 m/s de vitesse au bas de la fenêtre. v = 7,9 m/s ; v 0 = 14,1 m/s

    103. a. v = 5,42 m/s

    b. v = 4,64 m/s

    c. a = 2874,28 m/s 2

    d. (x − x 0) = 5,11 x 10 -3 m

    105. Supposons que les joueurs tombent du repos à une hauteur de 1,0 m et 0,3 m. 0,9 s ; 0,5 s

    107. a. t = 6,37 s prenant la racine positive

    b. v = 59,5 m/s

    109. a. y = 4,9 m

    b. v = 38,3 m/s ; environ −33,3 m

    111. h =\(\frac{1}{2}\) gt 2, h = hauteur totale et temps de chute au sol\(\frac{2}{3}\) h =\(\frac{1}{2}\) g (t − 1) 2 en t — 1 seconde il tombe\(\frac{2}{3}\) h$$ \ frac {2} {3} \ left (\ dfrac {1} {2} gt^ {2} \ right) = \ frac {1} {2} g (t − 1) ^ {2} \ ; ou \ ; \ frac {t^ {2}} {3} = \ frac {1} {2} (t − 1) ^ {2} $ $0$ = t^ {2} − 6 t + 3, \ ; t = \ frac {6 \ pm \ sqrt {62 − 4 \ cdotp 3}} {2} = 3 \ pm \ frac {\ sqrt {24}} {2} $$ t = 5,45 s et h = 145,5 m. L'autre racine est inférieure à 1 s. Vérifiez que t = 4,45 s, h =\(\frac{1}{2}\) gt 2 = 97,0 m =\(\frac{2}{3}\) (145,5)

    Problèmes liés au défi

    113. a. v (t) = 10 t − 12 t 2 m/s, a (t) = 10 − 24 t m/s 2

    b. v (2 s) = −28 m/s, a (2 s) = −38 m/s 2

    c. La pente de la fonction de position est nulle ou la vitesse est nulle. Deux solutions sont possibles : t = 0, qui donne x = 0, ou t =\(\frac{10.0}{12.0}\) = 0,83 s, qui donne x = 1,16 m. La deuxième réponse est le bon choix

    environ 0,83 s

    E. 1,16 m

    115. 96 km/h = 26,67 m/s, a\(\frac{26.67\; m/s}{4.0\; s}\) = 6,67 m/s 2, 295,38 km/h = 82,05 m/s, t = 12,3 s de temps pour accélérer jusqu'à la vitesse maximale ; x = 504,55 m = distance parcourue pendant l'accélération ; 7495,44 m à vitesse constante ;\(\frac{7495.44\; m}{82.05\; m/s}\) = 91,35 s, donc le temps total est de 91,35 s + 12,3 s = 103,65 s.