18.4 : Mouvement en deux et trois dimensions

Last updated
Save as PDF

Page ID: 191303

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Vérifiez votre compréhension

4.1. (a) En prenant la dérivée par rapport au temps de la fonction de position, nous avons$\vec{v}$ (t) = 9,0t ²$\hat{i}$ et$\vec{v}$ (3,0s) = 81,0$\hat{i}$ m/s. (b) Comme la fonction de vitesse n'est pas linéaire, nous supposons que la vitesse moyenne n'est pas égale à la vitesse instantanée. Nous vérifions cela et trouvons $$ \ vec {v} _ {avg} = \ frac {\ vec {r} (t_ {2}) - \ vec {r} (t_ {1})} {t_ {2} - t_ {1}} = \ frac {\ vec {r} (4.0 \ ; s) - \ vec {r} (2.0 \ ; s)} {4,0 \ ; s - 2,0 \ ; s} = \ frac {(188,0 \ ; \ hat {i} - 20,0 \ ; \ hat {i}) \ ; m} {2,0 \ ; s} = 84,0 \ ; \ hat {i} \ ; m/s, $$ qui est différent de$\vec{v}$ (3,0 s) = 81,0$\hat{i}$ m/s.

4.2. Le vecteur d'accélération est constant et ne change pas avec le temps. Si a, b et c ne sont pas nuls, la fonction de vitesse doit être linéaire dans le temps. Nous avons$\vec{v}$ (t) =$\int \vec{a}$ dt =$\int$ (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) dt = (a$\hat{i}$ + b$\hat{j}$ + c$\hat{k}$) t m/s, puisque la prise de la dérivée de la fonction de vitesse produit$\vec{a}$ (t). Si l'une des composantes de l'accélération est nulle, alors cette composante de la vitesse serait une constante.

4.3. (a) Choisissez le sommet de la falaise où la roche est projetée à partir de l'origine du système de coordonnées. Bien que cela soit arbitraire, nous choisissons généralement le temps t = 0 pour qu'il corresponde à l'origine. (b) L'équation qui décrit le mouvement horizontal est x = x ₀ + v _x t. Avec x _{0 = 0}, cette équation devient x = v _x t. (c) L'équation 4.27 à travers l'équation 4.29 et l'équation 4.46 décrivent le mouvement vertical, mais puisque y ₀ = 0 et v _0y = 0, ces équations se simplifient grandement pour devenir y =$\frac{1}{2}$ (v _0y _{+ v y}) t =$\frac{1}{2}$ v _y t, v _y = −gt, y = −$\frac{1}{2}$ gt ² et v _y ² = −2gy. (d) Nous utilisons les équations cinématiques pour déterminer les composantes x et y de la vitesse au point d'impact. En utilisant v _y ² = −2gy et en notant que le point d'impact est de −100,0 m, nous trouvons que la composante y de la vitesse à l'impact est v _y = 44,3 m/s. On nous donne la composante x, v _x = 15,0 m/s, de sorte que nous pouvons calculer la vitesse totale à l'impact : v = 46,8 m/s et$\theta$ = 71,3° en dessous de l'horizontale.

4.4. Le tir de golf à 30°.

4.5. 134,0 cm/s

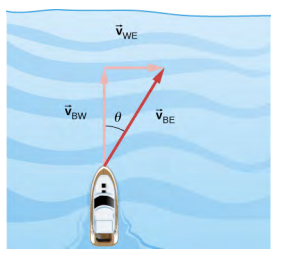
4.6. En étiquetant les indices de l'équation vectorielle, nous avons B = bateau, R = rivière et E = Terre. L'équation vectorielle devient$\vec{v}_{BE}$ =$\vec{v}_{BR}$ +$\vec{v}_{RE}$. Nous avons la géométrie du triangle droit illustrée dans la figure ci-dessous. Pour résoudre ce problème$\vec{v}_{BE}$, nous avons $$v_ {BE} = \ sqrt {v_ {BR} ^ {2} + v_ {RE} ^ {2}} = \ sqrt {4.5^ {2} + 3,0^ {2}} $$$v_ {BE} = 5,4 \ ; m/s, \ quad \ theta = \ tan^ {-1} \ left (\ dfrac {3.0} {4.5}} \ right) = 33,7^ {o} \ ldotp \]

Les vecteurs V sub B W, V sub W E et V sub B E forment un triangle droit. Un bateau est représenté au sommet où les queues du V sub B W et du V sub B E se rencontrent. Le vecteur V sous B W pointe vers le haut. V sub W E pointe vers la droite. V sub B E pointe vers le haut et vers la droite, formant un angle par rapport à la verticale. V sub B E est la somme vectorielle de v sub B W et V sub W E.

Questions conceptuelles

1. Ligne droite

3. La pente doit être nulle car le vecteur de vitesse est tangent au graphe de la fonction de position.

5. Non, les mouvements dans des directions perpendiculaires sont indépendants.

7. a. Non ; b. minimum au sommet de la trajectoire et maximum au lancement et à l'impact ; c. non, la vitesse est un vecteur ; d. oui, là où elle atterrit

9. Ils ont tous deux touché le sol en même temps.

11. Oui

13. S'il veut passer le ballon à un autre joueur, il doit garder un œil sur le référentiel dans lequel se trouvent les autres joueurs de l'équipe.

15.

Figure a : la trajectoire d'un chapeau est droite vers le bas. Figure b : La trajectoire d'un chapeau est parabolique, incurvée vers le bas et vers la gauche.

Problèmes

17. $\vec{r}$= 1,0$\hat{i}$ − 4,0$\hat{j}$ + 6,0$\hat{k}$

19. $\Delta \vec{r}_{Total}$= 472,0 m$\hat{i}$ + 80,3 m$\hat{j}$

21. Somme des déplacements = −6,4 km$\hat{i}$ + 9,4 km$\hat{j}$

23. a.$\vec{v}$ (t) = 8,0 t$\hat{i}$ + 6,0 t ²$\hat{k}$,$\vec{v}$ (0) = 0,$\vec{v}$ (1,0) = 8,0$\hat{i}$ + 6,0$\hat{k}$ m/s

b.$\vec{v}_{avg}$ = 4,0$\hat{i}$ + 2,0$\hat{k}$ m/s

25. $\Delta \vec{r}_{1}$= 20,00 m$\hat{j}$,$\Delta \vec{r}_{2}$ = (2 000 x 10 ⁴ m) (cos 30°$\hat{i}$ + sin 30°$\hat{j}$),$\Delta \vec{r}$ = 1 700 x 10 ⁴ m$\hat{i}$ + 1,002 x 10 ⁴ m$\hat{j}$

27. a.$\vec{v}$ (t) = (4,0 t$\hat{i}$ + 3,0 t$\hat{j}$) m/s,$\vec{r}$ (t) = (2,0 t ²$\hat{i}$ +$\frac{3}{2}$ t ²$\hat{j}$) m

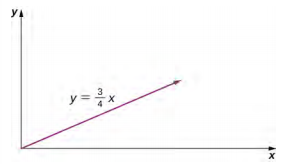
b. x (t) = 2,0 t 2 m, y (t) =$\frac{3}{2}$ t ² m, t ² =$\frac{x}{2} \Rightarrow$ y =$\frac{3}{4}$ x

Un graphique de la fonction linéaire y est égal à 3 quarts de x. Le graphique est une ligne droite à pente positive passant par l'origine.

29. a.$\vec{v}$ (t) = (6,0 t$\hat{i}$ − 21,0 t ²$\hat{j}$ + 10,0 t ⁻³$\hat{k}$) m/s

b.$\vec{a}$ (t) = (6,0$\hat{i}$ − 42,0 t$\hat{j}$ − 30 t ⁻⁴$\hat{k}$) m/s ²

c.$\vec{v}$ (2,0) = (12,0$\hat{i}$ − 84,0$\hat{j}$ + 1,25$\hat{k}$) m/s

d.$\vec{v}$ (1,0 s) = (6,0$\hat{i}$ − 21,0$\hat{j}$ + 10,0$\hat{k}$) m/s, |$\vec{v}$ (1,0 s) | = 24,0 m/s ;$\vec{v}$ (3,0 s) = (18,0$\hat{i}$ − 189,0$\hat{j}$ + 0,37$\hat{k}$) m/s, |$\vec{v}$ (3,0 s) | = 190,0 m/s

e.$\vec{r}$ (t) = (3,0 t ²$\hat{i}$ − 7,0 t ³$\hat{j}$ − 5,0 t ⁻²$\hat{k}$) cm,$\vec{v}_{avg}$ = (9,0$\hat{i}$ − 49,0$\hat{j}$ − 6,3$\hat{k}$) m/s

31. a.$\vec{v}$ (t) = −sin (1,0 t)$\hat{i}$ + cos (1,0 t)$\hat{j}$ +$\hat{k}$

b.$\vec{a}$ (t) = −cos (1,0 t)$\hat{i}$ − sin (1,0 t)$\hat{j}$

33. a. t = 0,55 s

b. x = 110 m

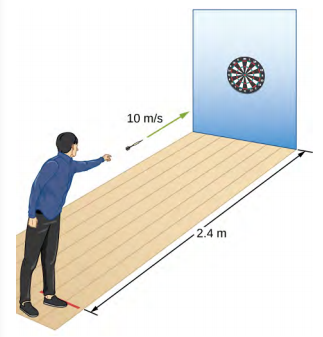
35. a. t = 0,24 s, d = 0,28 m

b. Ils visent haut.

Illustration d'une personne lançant une fléchette. La fléchette est lâchée horizontalement à une distance de 2,4 mètres du jeu de fléchettes, au niveau de l'œil de taureau du jeu de fléchettes, à une vitesse de 10 mètres par seconde.

37. a. t = 12,8 s, x = 5 619 m

b. v _y = 125,0 m/s, v _x = 439,0 m/s, |$\vec{v}$ | = 456,0 m/s

39. a. v _y = v _0y − gt, t = 10 s, v _y = 0, v _0y = 98,0 m/s, v ₀ = 196,0 m/s

b. h = 490,0 m

c. v _0x = 169,7 m/s, x = 3394,0 m

d. x = 2 545,5 m, y = 367,5 m,$\vec{s}$ = 2 545,5 m$\hat{i}$ + 367,5 m$\hat{j}$

41. −100 m = (−2,0 m/s) t − (4,9 m/s ²) à ², t = 4,3 s, x = 86,0 m

43. R _Lune = 48 m

45. a. v _0y = 24 m/s, v _y ² = v _0y ^{2 − 2} heures$\Rightarrow$ h = 23,4 m

b. t = 3 s, v _0x = 18 m/s, x = 54 m

c. y = −100 m, y ₀ = 0, y − y ₀ = v ₀ = v 0, t −$\frac{1}{2}$ gt ² − 100 = 24 t − 4,9 t ²$\Rightarrow$ t = 7,58 s

d. x = 136,44 m

e.$$ \ begin {split} t & = 2,0 \ ; s, y = 28,4 \ ; m, x = 36 \ ; m \ \ t & = 4,0 \ ; s, y = 17,6 \ ; m, x = 22,4 \ ; m \ \ t & = 6,0 \ ; s, y = −32,4 \ ; m, x = 108 \ ; m \ end {split} \]

47. v _0y = 12,9 m/s, y − y ₀ = v _0y t −$\frac{1}{2}$ gt ² − 20,0 = 12,9 t − 4,9 t ²

t = 3,7 s, v _{0 x} = 15,3 m/s$\Rightarrow$ x = 56,7 m

Le tir du golfeur atterrit donc à 13,3 m du green.

49. environ R = 60,8 m

b. R = 137,8 m

51. a. v _y ² = v _{0 y} ^{2 − 2} ans$\Rightarrow$ y = 2,9 m/s

y = 3,3 m/s

y =$\frac{v_{0y}^{2}}{2g}$ =$\frac{(v_{0} \sin \theta)^{2}}{2g} \Rightarrow \sin \theta$ = 0,91$\Rightarrow$$\theta$ = 65,5°

53. R = 18,5 m

55. y = (bronzage$\theta_{0}$) x −$\Big[ \frac{g}{2(v_{0} \cos \theta_{0})^{2}} \Big]$ x ²$\Rightarrow$ v ₀ = 16,4 m/s

57. R$\frac{v_{0}^{2} \sin 2 \theta_{0}}{g} \Rightarrow \theta_{0}$ = 15,0°

59. Il faut 1,1 s au récepteur large pour parcourir les 10 derniers mètres de sa course.

T _tof =$\frac{2(v_{0} \sin \theta)}{g} \Rightarrow \sin \theta$ = 0,27$\Rightarrow \theta$ = 15,6°

61. a _C = 40 m/s ²

63. a _C =$\frac{v^{2}}{r} \Rightarrow$ v ² = r, a _C = 78,4, v = 8,85 m/s

T = 5,68 s, soit 0,176 tr/min = 10,6 tr/min

65. Vénus se trouve à 108,2 millions de km du Soleil et a une période orbitale de 0,6152 ans.

r = 1,082 x 10 ¹¹ m, T = 1,94 x 10 ⁷ s

v = 3,5 x 10 ⁴ m/s, _C = 1,135 x 10 ⁻² m/s ²

67. 360 tr/min = 6 tr/min

v = 3,8 m/s, _C = 14,4 m/s ²

69. a. O′ (t) = (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) en m

b.$\vec{r}_{PS}$ =$\vec{r}_{PS'}$ +$\vec{r}_{S'S}$,$\vec{r}$ (t) =$\vec{r′}$ (t) + (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) à m

c.$\vec{v}$ (t) =$\vec{v′}$ (t) + (4,0$\hat{i}$ + 3,0$\hat{j}$ + 5,0$\hat{k}$) m/s

d. Les accélérations sont les mêmes.

71. $\vec{v}_{PC}$= (2,0$\hat{i}$ + 5,0$\hat{j}$ + 4,0$\hat{k}$) m/s

73. a. A = air, S = mouette, G = sol

$\vec{v}_{SA}$= 9,0 m/s, vitesse de la mouette par rapport à l'air calme

$\vec{v}_{AG}$= ? ,$\vec{v}_{SG}$ = 5 m/s,$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{AG} = \vec{v}_{SG} − \vec{v}_{SA}$

$\vec{v}_{AG}$= −4,0 m/s

b.$\vec{v}_{SG} = \vec{v}_{SA} + \vec{v}_{AG} \Rightarrow \vec{v}_{SG}$ = −13,0 m/s

$\frac{−6000\; m}{−13.0\; m/s}$= 7 min 42 s

75. Prenez la direction positive pour qu'elle soit la même que celle dans laquelle coule la rivière, c'est-à-dire vers l'est. S = rivage/terre, W = eau et B = bateau.

a.$\vec{v}_{BS}$ = 11 km/h, t = 8,2 min

b.$\vec{v}_{BS}$ = −5 km/h, t = 18 min

c.$\vec{v}_{BS} = \vec{v}_{BW} + \vec{v}_{WS}, \theta$ = 22° à l'ouest du nord

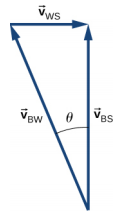
Les vecteurs V sub B W, V sub W S et V sub B S forment un triangle droit, avec V sub B W comme hypoténuse. V sub B S pointe vers le haut. V sub W S pointe vers la droite. V sub B W pointe vers le haut et vers la gauche, à un angle de thêta par rapport à la verticale. V sub B S est la somme vectorielle de v sub B W et V sub W S.

d. |$\vec{v}_{BS}$ | = 7,4 km/h, t = 6,5 min

e.$\vec{v}_{BS}$ = 8,54 km/h, mais seule la composante de la vitesse à travers la rivière est utilisée pour obtenir l'heure

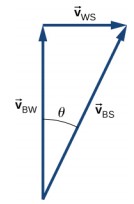
Les vecteurs V sub B W, V sub W S et V sub B S forment un triangle droit, avec V sub B S comme hypoténuse. V sous B W pointe vers le haut. V sub W S pointe vers la droite. V sub B S pointe vers le haut et vers la droite, à un angle de thêta par rapport à la verticale. V sub B S est la somme vectorielle de v sub B W et V sub W S.

t = 6,0 minutes

En aval = 0,3 km

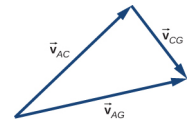
77. $\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

|$\vec{v}_{AC}$ | = 25 km/h, |$\vec{v}_{CG}$ | = 15 km/h, |$\vec{v}_{AG}$ | = 29,15 km/h,$\vec{v}_{AG} = \vec{v}_{AC} + \vec{v}_{CG}$

L'angle entre$\vec{v}_{AC}$ et$\vec{v}_{AG}$ est de 31°, donc la direction du vent est de 14° au nord de l'est.

Les vecteurs V sub A C, V sub C G et V sub A G forment un triangle. V sub A C et V sub C G sont à angle droit. V sub A G est la somme vectorielle de v sub A C et V sub C G.

Problèmes supplémentaires

79. a _C = 39,6 m/s ²

81. 90,0 km/h = 25,0 m/s, 9,0 km/h = 2,5 m/s, 60,0 km/h = 16,7 m/s

a _T = −2,5 m/s ², a _C = 1,86 m/s ², a = 3,1 m/s ²

83. Le rayon du cercle de révolution à la latitude$\lambda$ est R _E cos$\lambda$. La vitesse du corps est$\frac{2 \pi r}{T}$. a _C =$\frac{4 \pi^{2} R_{E} \cos \lambda}{T^{2}}$ pour$\lambda$ = 40°, a _C = 0,26 % g

85. a _T = 3,00 m/s ²

v (5 s) = 15,00 m/s, a _C = 150,00 m/s ²,$\theta$ = 88,8° par rapport à la tangente au cercle de révolution dirigé vers l'intérieur.

|$\vec{a}$ | = 150,03 m/s ²

87. $\vec{a}$(t) = −A$\omega^{2}$ cos$\omega$ t$\hat{i}$ − Un$\omega^{2}$ signe$\omega$ t$\hat{j}$

a _C = 5,0 m$\omega^{2}$,$\omega$ = 0,89 rad/s

$\vec{v}$(t) = −2,24 m/s$\hat{i}$ − 3,87 m/s$\hat{j}$

89. $\vec{r}_{1}$= 1,5$\hat{j}$ + 4,0$\hat{k}$,$\vec{r}_{2} = \Delta \vec{r} + \vec{r}_{1}$ = 2,5$\hat{i}$ + 4,7$\hat{j}$ + 2,8$\hat{k}$

91. v _x (t) = 265,0 m/s, v _y (t) = 20,0 m/s,$\vec{v}$ (5,0 s) = (265,0$\hat{i}$ + 20,0$\hat{j}$) m/s

93. R = 1,07 m

95. v ₀ = 20,1 m/s

97. v = 3 072,5 m/s, _C = 0,223 m/s ²

Problèmes liés au défi

99. a. −400,0 m = v _0y t − 4,9t ², 359,0 m = v _0x t, t =$\frac{359.0}{v_{0x}}$ − 400,0 = 359,0$\frac{v_{0y}}{v_{0x}}$ − 4,9$\left(\dfrac{359.0}{v_{0x}}\right)^{2}$

−400,0 = 359,0 à 40 −$\frac{631,516.9}{v_{0x}^{2}} \Rightarrow$ v _0x ² = 900,6, v _0x = 30,0 m/s, v _0y = v _0x tan 40 = 25,2 m/s, v = 39,2 m/s

b. t = 12,0 s

101. a.$\vec{r}_{TC}$ = (−32 + 80 t)$\hat{i}$ + 50 t$\hat{j}$, |$\vec{r}_{TC}$ | ² = (−32 + 80 t) ² + (50 t) ²

2r$\frac{dr}{dt}$ = 2 (−32 + 80 t) + 100 t,$\frac{dr}{dt} = \frac{2(−32 + 80t) + 100t}{2r}$ = 0

260 t = 64$\Rightarrow$ t = 15 minutes

b. |$\vec{r}_{TC}$ | = 17 km