16.5 : Énergie et puissance d'une vague

Objectifs d'apprentissage

• Expliquer comment l'énergie se déplace avec une impulsion ou une onde
• Décrire, à l'aide d'une expression mathématique, comment l'énergie d'une onde dépend de l'amplitude de l'onde

Toutes les vagues transportent de l'énergie, qui peut parfois être directement observée. Les tremblements de terre peuvent ébranler des villes entières et provoquer la destruction de milliers de boulets (Figure\(\PageIndex{1}\)). Les sons forts peuvent pulvériser les cellules nerveuses de l'oreille interne, provoquant une perte auditive permanente. Les ultrasons sont utilisés pour le traitement thermique profond des tensions musculaires. Un faisceau laser peut détruire une tumeur maligne. Les vagues envahissent les plages.

Figure\(\PageIndex{1}\) : L'effet destructeur d'un tremblement de terre est une preuve observable de l'énergie transportée par ces vagues. L'échelle de Richter pour évaluer les tremblements de terre est une échelle logarithmique liée à la fois à leur amplitude et à l'énergie qu'ils transportent.

Dans cette section, nous examinons l'expression quantitative de l'énergie dans les vagues. Cela sera d'une importance fondamentale dans les discussions ultérieures sur les ondes, du son à la lumière en passant par la mécanique quantique.

Énergie sous forme de vagues

La quantité d'énergie d'une onde est liée à son amplitude et à sa fréquence. Les séismes de grande amplitude produisent de grands déplacements du sol. Les sons forts ont des amplitudes de pression élevées et proviennent de vibrations de la source de plus grande amplitude que les sons doux. Les grands brise-océans remontent le rivage plus que les petits. Prenons l'exemple de la mouette et de la vague d'eau plus haut dans le chapitre (Figure 16.2.2). Le travail sur la mouette se fait par la vague lorsque la mouette remonte, modifiant ainsi son énergie potentielle. Plus l'amplitude est grande, plus la mouette est soulevée par la vague et plus le changement d'énergie potentielle est important.

L'énergie de l'onde dépend à la fois de l'amplitude et de la fréquence. Si l'énergie de chaque longueur d'onde est considérée comme un paquet d'énergie discret, une onde haute fréquence délivrera plus de ces paquets par unité de temps qu'une onde basse fréquence. Nous verrons que le taux moyen de transfert d'énergie dans les ondes mécaniques est proportionnel à la fois au carré de l'amplitude et au carré de la fréquence. Si deux ondes mécaniques ont des amplitudes égales, mais qu'une onde a une fréquence égale au double de la fréquence de l'autre, l'onde de fréquence la plus élevée aura un taux de transfert d'énergie quatre fois supérieur au taux de transfert d'énergie de l'onde de fréquence inférieure. Il convient de noter que, bien que le taux de transport d'énergie soit proportionnel au carré de l'amplitude et au carré de la fréquence dans les ondes mécaniques, le taux de transfert d'énergie dans les ondes électromagnétiques est proportionnel au carré de l'amplitude, mais indépendant de la fréquence.

La puissance des vagues

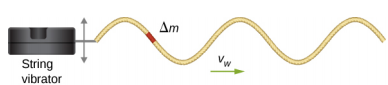
Prenons l'exemple d'une onde sinusoïdale sur une corde produite par un vibromasseur à cordes, comme le montre la figure\(\PageIndex{2}\). Le vibromasseur à cordes est un appareil qui fait vibrer une tige de haut en bas. Une chaîne de densité de masse linéaire uniforme est fixée à la tige, et la tige fait osciller la corde, produisant une onde sinusoïdale. La tige agit sur la corde, produisant de l'énergie qui se propage le long de la corde. Considérez un élément de masse de la chaîne avec une masse\(\Delta\) m, comme le montre la figure\(\PageIndex{2}\). Au fur et à mesure que l'énergie se propage le long de la corde, chaque élément de masse de la corde est entraîné de haut en bas à la même fréquence que l'onde. Chaque élément de masse de la corde peut être modélisé comme un oscillateur harmonique simple. Comme la chaîne a une densité linéaire constante\(\mu = \frac{\Delta m}{\Delta x}\), chaque élément de masse de la chaîne a la masse\(\Delta\) m =\(\mu \Delta\) x.

Figure\(\PageIndex{2}\) : Un vibromasseur à cordes est un appareil qui fait vibrer une tige. Une ficelle est attachée à la tige, et la tige agit sur la corde, entraînant la ficelle de haut en bas. Cela produit une onde sinusoïdale dans la corde, qui se déplace avec une vitesse d'onde v. La vitesse de la vague dépend de la tension de la corde et de la densité de masse linéaire de la corde. Une section de la corde de masse\(\Delta\) m oscille à la même fréquence que l'onde.

L'énergie mécanique totale de l'onde est la somme de son énergie cinétique et de son énergie potentielle. L'énergie cinétique K =\(\frac{1}{2}\) mv ² de chaque élément de masse de la chaîne de longueur\(\Delta\) x est\(\Delta\) K =\(\frac{1}{2}\) (\(\Delta\)m) v _y ², car l'élément de masse oscille perpendiculairement à la direction du mouvement de l'onde. En utilisant la densité de masse linéaire constante, l'énergie cinétique de chaque élément de masse de la chaîne de longueur\(\Delta\) x est

\[\Delta K = \frac{1}{2} (\mu \Delta x) v_{y}^{2} \ldotp \nonumber \]

Une équation différentielle peut être formée en laissant la longueur de l'élément de masse de la chaîne s'approcher de zéro,

\[dK = \lim_{\Delta x \rightarrow 0} \frac{1}{2} (\mu \Delta x) v_{y}^{2} = \frac{1}{2} (\mu\; dx)v_{y}^{2} \ldotp \nonumber \]

Comme l'onde est une onde sinusoïdale avec une fréquence angulaire\(\omega\), la position de chaque élément de masse peut être modélisée comme y (x, t) = A sin (kx −\(\omega\) t). Chaque élément de masse de la chaîne oscille avec une vitesse v _y =\(\frac{\partial y(x,t)}{\partial t}\) = −A\(\omega\) cos (kx −\(\omega\) t). L'énergie cinétique de chaque élément de masse de la corde devient

\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[-A \omega \cos(kx - \omega t)]^{2} \\ & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \ldotp \end{split}\]

L'onde peut être très longue et comporter de nombreuses longueurs d'onde. Pour normaliser l'énergie, considérez l'énergie cinétique associée à une longueur d'onde de l'onde. Cette énergie cinétique peut être intégrée sur la longueur d'onde pour trouver l'énergie associée à chaque longueur d'onde de l'onde :

\[\begin{split} dK & = \frac{1}{2} (\mu\; dx)[A^{2} \omega^{2} \cos^{2}(kx - \omega t)] \\ \int_{0}^{K_{\lambda}} dK & = \int_{0}^{\lambda} \frac{1}{2} \mu A^{2} \omega^{2} \cos^{2}(kx - \omega t) dx = \frac{1}{2} \mu A^{2} \omega^{2} \int_{0}^{\lambda} \cos^{2} (kx) dx, \\ K_{lambda} & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} x + \frac{1}{4k} \sin (2kx) \Big]_{0}^{\lambda} \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \Big[ \frac{1}{2} \lambda + \frac{1}{4k} \sin (2k \lambda) - \frac{1}{4k} \sin(0) \Big] \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

Il existe également de l'énergie potentielle associée à la vague. Tout comme la masse oscillant sur un ressort, il existe une force de rappel conservatrice qui, lorsque l'élément de masse est déplacé de la position d'équilibre, le ramène à la position d'équilibre. L'énergie potentielle de l'élément de masse peut être déterminée en considérant la force de rappel linéaire de la corde. Dans Oscillations, nous avons vu que l'énergie potentielle stockée dans un ressort avec une force de rappel linéaire est égale à U =\(\frac{1}{2}\) k _s x ², où l'équilibre la position est définie comme x = 0,00 m. Lorsqu'une masse attachée au ressort oscille selon un simple mouvement harmonique, la fréquence angulaire est égale à\(\omega = \frac{k_{s}}{m}\). Comme chaque élément de masse oscille selon un mouvement harmonique simple, la constante du ressort est égale à k _s =\(\Delta\)\(\omega^{2}\) m. L'énergie potentielle de l'élément de masse est égale à

\[\Delta U = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \Delta m \omega^{2} x^{2} \ldotp \nonumber \]

Notez que k _s est la constante du ressort et non le nombre d'onde k =\(\frac{2 \pi}{\lambda}\). Cette équation peut être utilisée pour déterminer l'énergie sur une longueur d'onde. En intégrant sur la longueur d'onde, nous pouvons calculer l'énergie potentielle sur une longueur d'onde :

\[\begin{split} dU & = \frac{1}{2} k_{s} x^{2} = \frac{1}{2} \mu \omega^{2} x^{2} dx, \\ U_{\lambda} & = \frac{1}{2} \mu \omega^{2} A^{2} \int_{0}^{\lambda} \sin^{2} (kx) dx = \frac{1}{4} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

L'énergie potentielle associée à une longueur d'onde de l'onde est égale à l'énergie cinétique associée à une longueur d'onde. L'énergie totale associée à une longueur d'onde est la somme de l'énergie potentielle et de l'énergie cinétique :

\[\begin{split} E_{\lambda} & = U_{\lambda} +K_{\lambda} \\ & = \frac{1}{4} \mu A^{2} \omega^{2} \lambda + \frac{1}{4} \mu A^{2} \omega^{2} \lambda \\ & = \frac{1}{2} \mu A^{2} \omega^{2} \lambda \ldotp \end{split}\]

La puissance moyenne temporelle d'une onde mécanique sinusoïdale, qui est le taux moyen de transfert d'énergie associé à une onde lorsqu'elle passe un point, peut être déterminée en divisant l'énergie totale associée à l'onde par le temps nécessaire pour transférer l'énergie. Si la vitesse de l'onde sinusoïdale est constante, le temps nécessaire pour qu'une longueur d'onde passe par un point est égal à la période de l'onde, qui est également constante. Pour une onde mécanique sinusoïdale, la puissance moyenne dans le temps est donc l'énergie associée à une longueur d'onde divisée par la période de l'onde. La longueur d'onde de l'onde divisée par la période est égale à la vitesse de l'onde,

\[P_{ave} = \frac{E_{\lambda}}{T} = \frac{1}{2} \mu A^{2} \omega^{2} \frac{\lambda}{T} = \frac{1}{2} \mu A^{2} \omega^{2} v \ldotp \label{16.10}\]

Notez que cette équation de la puissance moyenne temporelle d'une onde mécanique sinusoïdale montre que la puissance est proportionnelle au carré de l'amplitude de l'onde et au carré de la fréquence angulaire de l'onde. Rappelez-vous que la fréquence angulaire est égale à\(\omega\) = 2\(\pi\) f, donc la puissance d'une onde mécanique est égale au carré de l'amplitude et au carré de la fréquence de l'onde.

Exemple 16.6 : Alimentation fournie par un vibromasseur à cordes

Prenons l'exemple d'une corde de deux mètres de long d'une masse de 70,00 g attachée à un vibromasseur à cordes, comme illustré à la figure\(\PageIndex{2}\). La tension dans la corde est de 90,0 N. Lorsque le vibromasseur à cordes est allumé, il oscille à une fréquence de 60 Hz et produit une onde sinusoïdale sur la corde d'une amplitude de 4,00 cm et d'une vitesse d'onde constante. Quelle est la puissance moyenne dans le temps fournie à l'onde par le vibromasseur à cordes ?

Stratégie

La puissance fournie à l'onde doit être égale à la puissance moyenne temporelle de l'onde sur la corde. Nous connaissons la masse de la corde (m _s), la longueur de la corde (L _s) et la tension (F _T) de la corde. La vitesse de l'onde sur la corde peut être dérivée de la densité de masse linéaire et de la tension. La corde oscille à la même fréquence que le vibromasseur à cordes, à partir de laquelle on peut trouver la fréquence angulaire.

Solution

1. Commencez par l'équation de la puissance moyenne temporelle d'une onde sinusoïdale sur une corde : $$P = \ frac {1} {2} \ mu A^ {2} \ omega^ {2} v \ lDotp$$L'amplitude est donnée, nous devons donc calculer la densité de masse linéaire de la corde, la fréquence angulaire de l'onde sur la corde et la vitesse de l'onde sur la corde.
2. Nous devons calculer la densité linéaire pour déterminer la vitesse des vagues : $$ \ mu = \ frac {m_ {s}} {L_ {s}} = \ frac {0,070 \ ; kg} {2,00 \ ; m} = 0,035 \ ; kg/m \ ldotp$$
3. La vitesse des vagues peut être déterminée en utilisant la densité de masse linéaire et la tension de la corde : $$v = \ sqrt {\ frac {F_ {T}} {\ mu}} = \ sqrt {\ frac {90,00 \ ; N} {0,035 \ ; kg/m}} = 50,71 \ ; m/s \ ldotp$$
4. La fréquence angulaire peut être trouvée à partir de la fréquence : $$ \ omega = 2 \ pi f = 2 \ pi (60 \ ; s^ {-1}) = 376,80 \ ; s^ {-1} \ ldotp$$
5. Calculez la puissance moyenne dans le temps : $$P = \ frac {1} {2} \ mu A^ {2} \ omega^ {2} v = \ frac {1} {2} (0,035 \ ; kg/m) (0,040 \ ; m) ^ {2} (376,80 \ ; s^ {-1}) ^ {2} (50,71 \ ; m/s) = 201,5 \ ; W \ ldoldol tp$$

L'importance

La puissance moyenne temporelle d'une onde sinusoïdale est proportionnelle au carré de l'amplitude de l'onde et au carré de la fréquence angulaire de l'onde. Cela est vrai pour la plupart des ondes mécaniques. Si la fréquence angulaire ou l'amplitude de l'onde étaient doublées, la puissance augmenterait d'un facteur quatre. La puissance moyenne temporelle de l'onde sur une corde est également proportionnelle à la vitesse de l'onde sinusoïdale sur la corde. Si la vitesse était doublée, en multipliant la tension par quatre, la puissance serait également doublée.

Exercice 16.6

La puissance moyenne temporelle d'une onde sinusoïdale sur une corde est-elle proportionnelle à la densité linéaire de la corde ?

Les équations pour l'énergie de l'onde et la puissance moyenne dans le temps ont été dérivées pour une onde sinusoïdale sur une corde. En général, l'énergie d'une onde mécanique et sa puissance sont proportionnelles à l'amplitude au carré et à la fréquence angulaire au carré (et donc à la fréquence au carré).

Une autre caractéristique importante des vagues est leur intensité. Les vagues peuvent également être concentrées ou étalées. Les ondes d'un tremblement de terre, par exemple, se répandent sur une plus grande surface lorsqu'elles s'éloignent d'une source, de sorte qu'elles causent moins de dégâts à mesure qu'elles s'éloignent de la source. La modification de la zone couverte par les vagues a des effets importants. Tous ces facteurs pertinents sont inclus dans la définition de l'intensité (I) en tant que puissance par unité de surface :

\[I = \frac{P}{A}, \label{16.11}\]

où P est la puissance transportée par l'onde à travers la zone A. La définition de l'intensité est valable pour toute énergie en transit, y compris celle véhiculée par les vagues. L'unité SI pour l'intensité est le watt par mètre carré (W/m ²). De nombreuses ondes sont des ondes sphériques qui sortent d'une source sous forme de sphère. Par exemple, un haut-parleur monté sur un poteau au-dessus du sol peut produire des ondes sonores qui s'éloignent de la source sous la forme d'une onde sphérique. Les ondes sonores sont abordées plus en détail dans le chapitre suivant, mais en général, plus vous vous éloignez du haut-parleur, moins le son que vous entendez est intense. Lorsqu'une onde sphérique s'éloigne d'une source, sa surface augmente à mesure que son rayon augmente (A = 4\(\pi\) r ²). L'intensité d'une onde sphérique est donc

\[I = \frac{P}{4 \pi r^{2}} \ldotp \label{16.12}\]

S'il n'y a pas de forces dissipatives, l'énergie restera constante à mesure que l'onde sphérique s'éloigne de la source, mais l'intensité diminuera à mesure que la surface augmente.

Dans le cas de l'onde circulaire bidimensionnelle, l'onde se déplace vers l'extérieur, augmentant la circonférence de l'onde à mesure que le rayon du cercle augmente. Si vous lancez un caillou dans un étang, l'ondulation de la surface se déplace sous la forme d'une onde circulaire. Lorsque l'ondulation s'éloigne de la source, l'amplitude diminue. L'énergie de l'onde se répand sur une plus grande circonférence et l'amplitude diminue proportionnellement et non\(\frac{1}{r^{2}}\), comme dans le cas d'une onde sphérique.\(\frac{1}{r}\)