16.4 : Vitesse des vagues sur une corde tendue
- Page ID
- 191235
- Déterminez les facteurs qui influent sur la vitesse d'une vague sur une corde
- Écrivez une expression mathématique pour la vitesse d'une onde sur une chaîne et généralisez ces concepts à d'autres supports
La vitesse d'une vague dépend des caractéristiques du milieu. Par exemple, dans le cas d'une guitare, les cordes vibrent pour produire le son. La vitesse des ondes sur les cordes et la longueur d'onde déterminent la fréquence du son produit. Les cordes d'une guitare ont une épaisseur différente mais peuvent être fabriquées dans un matériau similaire. Ils ont des densités linéaires différentes, la densité linéaire étant définie comme la masse par longueur,
\[\mu = \frac{\text{mass of string}}{\text{length of string}} = \frac{m}{l} \ldotp \label{16.7}\]
Dans ce chapitre, nous ne considérons que les chaînes ayant une densité linéaire constante. Si la densité linéaire est constante, alors la masse (\(\Delta m\)) d'une petite longueur de chaîne (\(\Delta\)x) est\(\Delta m = \mu \Delta x\). Par exemple, si la corde a une longueur de 2,00 m et une masse de 0,06 kg, la densité linéaire est de\(\mu = \frac{0.06\; kg}{2.00\; m}\) = 0,03 kg/m. Si une section de 1 mm est découpée dans la corde, la masse de la longueur de 1 mm est
\[ \Delta m = \mu \Delta x = (0.03\, kg/m)(0.001\, m) = 3.00 \times 10^{−5}\, kg. \nonumber\]
La guitare dispose également d'une méthode pour modifier la tension des cordes. La tension des cordes est réglée en faisant tourner des broches, appelées chevilles d'accord, autour desquelles les cordes sont enroulées. Pour la guitare, la densité linéaire de la corde et la tension de la corde déterminent la vitesse des ondes dans la corde et la fréquence du son produit est proportionnelle à la vitesse des vagues.
Vitesse des vagues sur une corde sous tension
Pour voir comment la vitesse d'une onde sur une corde dépend de la tension et de la densité linéaire, considérez une impulsion envoyée le long d'une corde tendue (Figure\(\PageIndex{1}\)). Lorsque la corde tendue est au repos à la position d'équilibre, la tension dans la corde\(F_T\) est constante. Considérons un petit élément de la chaîne avec une masse égale à\(\Delta m = \mu \Delta x\). L'élément de masse est au repos et en équilibre et la force de tension de chaque côté de l'élément de masse est égale et opposée.
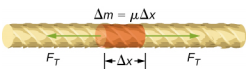
Si vous arrachez une corde sous tension, une onde transversale se déplace dans la direction X positive, comme le montre la figure\(\PageIndex{2}\). L'élément de masse est petit mais est agrandi sur la figure pour le rendre visible. L'élément de faible masse oscille perpendiculairement au mouvement des vagues sous l'effet de la force de rappel fournie par la corde et ne se déplace pas dans la direction X. La tension F T dans la corde, qui agit dans les directions X positive et négative, est approximativement constante et est indépendante de la position et du temps.
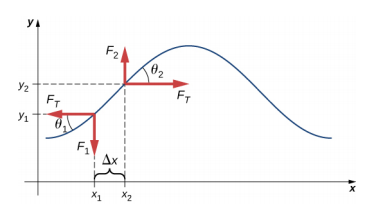
Supposons que l'inclinaison de la corde déplacée par rapport à l'axe horizontal soit faible. La force nette exercée sur l'élément de la corde, agissant parallèlement à la corde, est la somme de la tension de la corde et de la force de rappel. Les composantes X de la force de tension s'annulent, de sorte que la force nette est égale à la somme des composantes y de la force. L'amplitude de la composante X de la force est égale à la force horizontale de tension de la corde,\(F_T\) comme indiqué sur la figure\(\PageIndex{2}\). Pour obtenir les composantes Y de la force, notez que tan\(\theta_{1} = − \frac{F_{1}}{F_{T}}\) et\(\tan \theta_{2} = \frac{F_{2}}{F_{T}}\). La valeur\(\tan \theta\) est égale à la pente d'une fonction en un point, qui est égale à la dérivée partielle de y par rapport à x à ce point. Par conséquent,\(\frac{F_{1}}{F_{T}}\) est égal à la pente négative de la chaîne à x 1 et\(\frac{F_{2}}{F_{T}}\) est égal à la pente de la chaîne à x 2 :
\[\frac{F_{1}}{F_{T}} = - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}}\; and\; \frac{F_{2}}{F_{T}} = \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} \ldotp\]
La force nette exercée sur l'élément de petite masse peut être écrite comme
\[F_{net} = F_{1} + F_{2} = F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] \ldotp\]
Selon la deuxième loi de Newton, la force nette est égale à la masse multipliée par l'accélération. La densité linéaire de la chaîne µ est la masse par longueur de la corde, et la masse de la partie de la chaîne est\(\mu \Delta\) x,
\[F_{T} \Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg] = \Delta ma = \mu \Delta x \left(\frac{\partial^{2} y}{\partial t^{2}}\right) \ldotp\]
En divisant par F T\(\Delta\) x et en prenant la limite\(\Delta\) lorsque x approche zéro,
\[\begin{split} \lim_{\Delta x \rightarrow 0} \frac{\Bigg[ \left(\dfrac{\partial y}{\partial x}\right)_{x_{2}} - \left(\dfrac{\partial y}{\partial x}\right)_{x_{1}} \Bigg]}{\Delta x} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \\ \frac{\partial^{2} y}{\partial x^{2}} & = \frac{\mu}{F_{T}} \frac{\partial^{2} y}{\partial t^{2}} \ldotp \end{split}\]
Rappelons que l'équation d'onde linéaire est
\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]
Par conséquent,
\[\frac{1}{v^{2}} = \frac{\mu}{F_{T}} \ldotp\]
En résolvant cela\(v\), nous voyons que la vitesse de l'onde sur une corde dépend de la tension et de la densité linéaire
La vitesse d'une impulsion ou d'une onde sur une corde sous tension peut être déterminée à l'aide de l'équation
\[|v| = \sqrt{\frac{F_{T}}{\mu}} \label{16.8}\]
où\(F_T\) est la tension dans la corde et\(µ\) la masse par longueur de la corde.
Sur une guitare à six cordes, la corde en mi haut a une densité linéaire de\(\mu_{High\; E}\) = 3,09 x 10 -4 kg/m et la corde en mi bas a une densité linéaire de\(\mu_{Low\; E}\) = 5,78 x 10 -3 kg/m. (a) Si la corde en mi haut est pincée, produisant une onde dans la corde, quelle est la vitesse de l'onde si la tension de la corde est de 56,40 N ? (b) La densité linéaire de la chaîne en E bas est environ 20 fois supérieure à celle de la chaîne en E haut. Pour que les vagues traversent la corde en mi bas à la même vitesse que le mi haut, la tension devrait-elle être supérieure ou inférieure à celle de la corde en mi haut ? Quelle serait la tension approximative ? (c) Calculez la tension de la corde en mi bas nécessaire pour la même vitesse de vague.
Stratégie
- La vitesse de l'onde peut être déterminée à partir de la densité linéaire et de la tension\(v = \sqrt{\frac{F_{T}}{\mu}}\).
- À partir de l'équation v =\(\sqrt{\frac{F_{T}}{\mu}}\), si la densité linéaire est augmentée d'un facteur de près de 20, la tension devrait être augmentée d'un facteur 20.
- Connaissant la vitesse et la densité linéaire, l'équation de vitesse peut être résolue pour la force de tension F T =\(\mu\) v 2.
Solution
- Utilisez l'équation de vitesse pour déterminer la vitesse : $$v = \ sqrt {\ frac {F_ {T}} {\ mu}} = \ sqrt {\ frac {56,40 \ ; N} {3,09 \ times 10^ {-4} \ ; kg/m}} = 427,23 \ ; m/s \ ldotp$$
- La tension devrait être multipliée par environ 20. La tension serait légèrement inférieure à 1128 N.
- Utilisez l'équation de vitesse pour déterminer la tension réelle : $$F_ {T} = \ mu v^ {2} = (5,78 \ times 10^ {-3} \ ; kg/m) (427,23 \ ; m/s) ^ {2} = 1055,00 \ ; N \ ldotp$$
- Cette solution se situe à moins de 7 % de l'approximation.
L'importance
Les notes standard des six cordes (mi aigu, B, G, D, A, mi grave) sont accordées pour vibrer aux fréquences fondamentales (329,63 Hz, 246,94 Hz, 196,00 Hz, 146,83 Hz, 110,00 Hz et 82,41 Hz) lorsqu'elles sont pincées. Les fréquences dépendent de la vitesse des ondes sur la corde et de la longueur d'onde des ondes. Les six cordes ont des densités linéaires différentes et sont « accordées » en modifiant les tensions des cordes. Nous verrons dans Interference of Waves que la longueur d'onde dépend de la longueur des chaînes et des conditions limites. Pour jouer des notes autres que les notes fondamentales, la longueur des cordes est modifiée en appuyant sur les cordes.
La vitesse d'onde d'une vague sur une corde dépend de la tension et de la densité de masse linéaire. Si la tension est doublée, qu'arrive-t-il à la vitesse des vagues sur la corde ?
Vitesse des ondes de compression dans un fluide
La vitesse d'une vague sur une corde dépend de la racine carrée de la tension divisée par la masse par longueur, la densité linéaire. En général, la vitesse d'une onde à travers un milieu dépend de la propriété élastique du milieu et de la propriété inertielle du milieu.
\[|v| = \sqrt{\frac{elastic\; property}{inertial\; property}}\]
La propriété élastique décrit la tendance des particules du milieu à revenir à leur position initiale lorsqu'elles sont perturbées. La propriété inertielle décrit la tendance de la particule à résister aux changements de vitesse.
La vitesse d'une onde longitudinale à travers un liquide ou un gaz dépend de la densité du fluide et du module volumique du fluide,
\[v = \sqrt{\frac{\beta}{\rho}} \ldotp \label{16.9}\]
Ici, le module global est défini comme Β =\(− \frac{\Delta P}{\frac{\Delta V}{V_{0}}}\), où\(\Delta\) P est la variation de la pression et le dénominateur est le rapport entre la variation de volume et le volume initial, et\(\rho \equiv \frac{m}{V}\) est la masse par unité de volume. Par exemple, le son est une onde mécanique qui traverse un fluide ou un solide. La vitesse du son dans l'air soumis à une pression atmosphérique de 1,013 x 10 5 Pa et à une température de 20 °C est v s ≈ 343,00 m/s. Comme la densité dépend de la température, la vitesse du son dans l'air dépend de la température de l'air. Cela sera discuté en détail dans Sound.


