16.3 : Mathématiques des ondes

Objectifs d'apprentissage

• Modélisez une onde se déplaçant avec une vitesse d'onde constante à l'aide d'une expression mathématique
• Calculez la vitesse et l'accélération du milieu
• Montrez en quoi la vitesse du milieu diffère de la vitesse de l'onde (vitesse de propagation)

Dans la section précédente, nous avons décrit les ondes périodiques en fonction de leurs caractéristiques de longueur d'onde, de période, d'amplitude et de vitesse d'onde de l'onde. Les ondes peuvent également être décrites par le mouvement des particules du milieu dans lequel elles se déplacent. La position des particules du milieu peut être modélisée mathématiquement sous forme de fonction d'onde s, qui peut être utilisée pour déterminer la position, la vitesse et l'accélération des particules du milieu de l'onde à tout moment.

Pouls

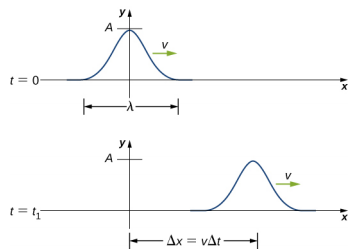
Une impulsion peut être décrite comme une onde constituée d'une seule perturbation qui se déplace dans le milieu avec une amplitude constante. L'impulsion se déplace selon un schéma qui conserve sa forme lorsqu'elle se propage à une vitesse d'onde constante. Comme la vitesse de l'onde est constante, la distance parcourue par l'impulsion en un temps Δt est égale à Δx = VΔt (Figure\(\PageIndex{1}\)).

Figure\(\PageIndex{1}\) : L'impulsion à l'instant t = 0 est centrée sur x = 0 avec une amplitude A. L'impulsion se déplace comme un motif de forme constante, avec une valeur maximale constante A. La vitesse est constante et l'impulsion se déplace sur une distance Δx = VΔt en un temps Δt. La distance parcourue est mesurée avec n'importe quel point approprié du pouls. Sur cette figure, la crête est utilisée.

Modélisation d'une onde sinusoïdale unidimensionnelle avec une fonction d'onde

Prenons l'exemple d'une corde maintenue à une tension constante dont une extrémité est fixe et\(F_T\) où l'extrémité libre est oscillée entre\(y = +A\) et\(y = −A\) par un dispositif mécanique à une fréquence constante. La figure\(\PageIndex{2}\) montre des instantanés de la vague à un intervalle d'un huitième de période, commençant après une période (\(t = T\)).

Figure\(\PageIndex{2}\) : Instantanés d'une onde transversale se déplaçant à travers une corde sous tension, commençant à l'heure\(t = T\) et pris à intervalles de\(\frac{1}{8}T\). Les points colorés sont utilisés pour mettre en évidence les points de la chaîne. Les points séparés d'une longueur d'onde dans la direction x sont surlignés par des points de même couleur.

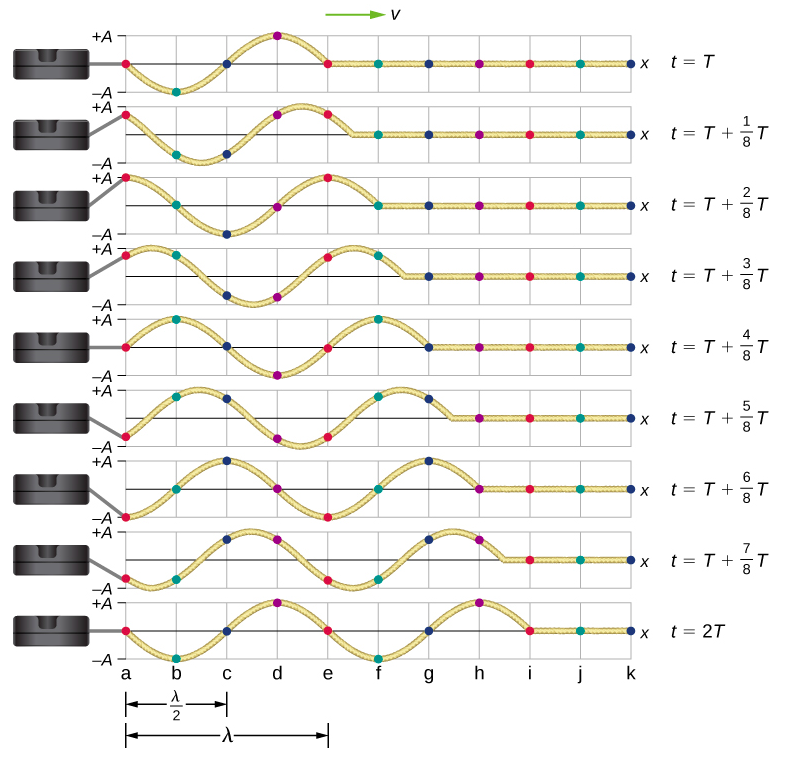
Notez que chaque point sélectionné de la chaîne (marqué par des points de couleur) oscille de haut en bas dans un mouvement harmonique simple, entre\(y = +A\) et\(y = −A\), avec un point\(T\). L'onde sur la corde est sinusoïdale et se traduit dans la direction X positive au fil du temps.

À ce stade, il est utile de se rappeler, d'après votre étude de l'algèbre, que s'il s'\(f(x)\)agit d'une fonction, la même fonction\(f(x−d)\) est traduite dans la direction x positive par une distance\(d\). La fonction\(f(x+d)\) est la même fonction traduite dans la direction X négative par une distance\(d\). Nous voulons définir une fonction d'onde qui donnera la\(y\) position -de chaque segment de la chaîne pour chaque position x le long de la chaîne à chaque fois\(t\).

En regardant le premier instantané de la figure\(\PageIndex{2}\), la position y de la chaîne entre\(x = 0\) et\(x = λ\) peut être modélisée comme une fonction sinusoïdale. Cette onde se propage le long de la chaîne une longueur d'onde par période, comme on peut le voir sur le dernier cliché. L'onde se déplace donc avec une vitesse d'onde constante de\(v = λ/T\).

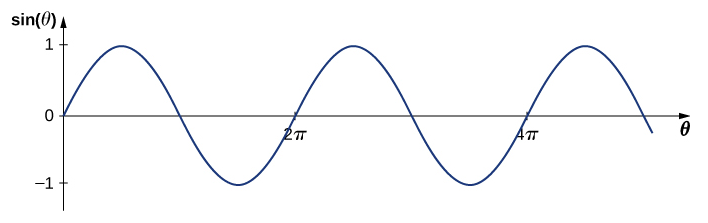
Rappelons qu'une fonction sinusoïdale est une fonction de l'angle\(θ\), oscillant entre +1 et -1, et se répétant tous les\(2π\) radians (Figure\(\PageIndex{3}\)). Cependant, la position y du milieu, ou fonction d'onde, oscille entre\(+A\) et\(−A\), et répète toutes les longueurs d'onde\(λ\).

Figure\(\PageIndex{3}\) : Une fonction sinusoïdale oscille entre +1 et −1 tous les 2π radians.

Pour construire notre modèle de l'onde à l'aide d'une fonction périodique, considérez le rapport entre l'angle et la position,

\[\begin{align*} \dfrac{\theta}{x} &=\frac{2 \pi}{\lambda}, \\[4pt] \theta &=\frac{2 \pi}{\lambda} x. \end{align*}\]

En utilisant\(\theta = \frac{2\pi}{\lambda}x\) et en multipliant la fonction sinus par l'amplitude A, nous pouvons maintenant modéliser la position y de la chaîne en fonction de la position x :

\[ y(x)=A \sin \left(\frac{2 \pi}{\lambda} x\right). \nonumber \]

L'onde sur la corde se déplace dans la direction x positive avec une vitesse v constante et se déplace sur une distance vt en un temps t. La fonction d'onde peut désormais être définie par

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda}(x-v t)\right). \nonumber \]

Il est souvent pratique de réécrire cette fonction d'onde sous une forme plus compacte. En multipliant le résultat par le ratio\(\frac{2\pi}{\lambda}\), on obtient l'équation

\[ y(x, t)=A \sin \left(\frac{2 \pi}{\lambda} x-\frac{2 \pi}{\lambda} v t\right). \nonumber \]

La valeur\(\frac{2\pi}{\lambda}\) est définie comme le numéro de vague. Le symbole du nombre d'ondes est k et possède des unités de mètres inverses, m ^-1 :

\[ k \equiv \frac{2 \pi}{\lambda} \label{16.2} \]

Rappelons dans Oscillations que la fréquence angulaire est définie comme\(\omega \equiv \frac{2\pi}{T}\). Le deuxième terme de la fonction d'onde devient

\[\frac{2 \pi}{\lambda} v t=\frac{2 \pi}{\lambda}\left(\frac{\lambda}{T}\right) t=\frac{2 \pi}{T} t=\omega t. \nonumber \]

La fonction d'onde pour une onde harmonique simple sur une corde se réduit à

\[ y(x, t)=A \sin (k x \mp \omega t) \nonumber \]

où A est l'amplitude,\(k = \frac{2\pi}{\lambda}\) est le nombre d'ondes,\(\omega = \frac{2\pi}{T}\) est la fréquence angulaire, le signe moins est pour les ondes se déplaçant dans la direction positive x et le signe plus est pour les ondes se déplaçant dans la direction x négative. La vitesse de l'onde est égale à

\[ v=\frac{\lambda}{T}=\frac{\lambda}{T}\left(\frac{2 \pi}{2 \pi}\right)=\frac{\omega}{k} \label{16.3} .\]

Repensez à notre discussion sur une masse sur un ressort, lorsque la position de la masse était modélisée comme

\[x(t) = A \cos(ωt+ϕ). \nonumber\]

L'angle\(ϕ\) est un décalage de phase, ajouté pour tenir compte du fait que la masse peut avoir des conditions initiales autres que\(x = +A\) et\(v = 0\). Pour des raisons similaires, la phase initiale est ajoutée à la fonction d'onde. La fonction d'onde modélisant une onde sinusoïdale, permettant un décalage de phase initial\(ϕ\), est

\[ y(x, t)=A \sin (k x \mp \omega t+\phi) \label{16.4} \]

La valeur

\[ (k x \mp \omega t+\phi) \label{16.5} \]

est connue sous le nom de phase de l'onde, où\(\phi\) est la phase initiale de la fonction d'onde. Le fait que le terme temporel\(\omega t\) soit négatif ou positif dépend de la direction de l'onde. Considérons d'abord le signe moins d'une onde dont la phase initiale est égale à zéro (\(\phi\)= 0). La phase de la vague serait (\(kx = \omega t\)). Envisagez de suivre un point sur une vague, comme une crête. Une crête se produira quand\(\sin(kx - \omega t = 1.00\), c'est-à-dire quand\(k x-\omega t=n \pi+\frac{\pi}{2}\), pour toute valeur intégrale de n. Par exemple, une crête particulière se trouve à\(k x-\omega t=\frac{\pi}{2}\). Au fur et à mesure que l'onde se déplace, le temps augmente et x doit également augmenter pour que la phase reste égale à\(\frac{\pi}{2}\). Par conséquent, le signe moins correspond à une onde se déplaçant dans la direction x positive. En utilisant le signe plus,\(k x+\omega t=\frac{\pi}{2}\). Au fur et à mesure que le temps augmente, x doit diminuer pour que la phase reste égale à\(\frac{\pi}{2}\). Le signe plus est utilisé pour les vagues se déplaçant dans la direction X négative. En résumé,\(y(x, t)=A \sin (k x-\omega t+\phi)\) modélise une onde se déplaçant dans la direction x positive et\(y(x, t)=A \sin (k x+\omega t+\phi)\) modélise une onde se déplaçant dans la direction x négative.

L'équation \ ref {16.4} est connue sous le nom de fonction d'onde harmonique simple. Une fonction d'onde est une fonction telle que\(f(x, t)=f(x-v t)\). Plus loin dans ce chapitre, nous verrons qu'il s'agit d'une solution à l'équation des ondes linéaires. Notez que cela\(y(x, t)=A \cos \left(k x+\omega t+\phi^{\prime}\right)\) fonctionne tout aussi bien car cela correspond à un décalage de phase différent\(\phi^{\prime}=\phi-\frac{\pi}{2}\).

Déterminer les caractéristiques d'une onde sinusoïdale

1. Pour déterminer l'amplitude, la longueur d'onde, la période et la fréquence d'une onde sinusoïdale, notez la fonction d'onde dans le formulaire\(y(x, t)=A \sin (k x-\omega t+\phi)\).
2. L'amplitude peut être lue directement à partir de l'équation et est égale à\(A\).
3. La période de l'onde peut être dérivée de la fréquence angulaire\( \left(T=\frac{2 \pi}{\omega}\right)\).
4. La fréquence peut être trouvée en utilisant\(f = \frac{1}{T}\)
5. La longueur d'onde peut être trouvée à l'aide du numéro d'onde\(\left(\lambda=\frac{2 \pi}{k}\right)\).

Exemple\(\PageIndex{1}\): Characteristics of a traveling wave on a string

Une onde transversale sur une corde tendue est modélisée à l'aide de la fonction d'onde

\[ \begin{align*} y(x, t) &=A \sin (k x-w t) \\[4pt] &= (0.2 \: \mathrm{m}) \sin \left(6.28 \: \mathrm{m}^{-1} x-1.57 \: \mathrm{s}^{-1} t\right) \end{align*} \]

Déterminez l'amplitude, la longueur d'onde, la période et la vitesse de l'onde.

Stratégie

Toutes ces caractéristiques de l'onde peuvent être trouvées à partir des constantes incluses dans l'équation ou à partir de combinaisons simples de ces constantes.

Solution

1. L'amplitude, le nombre d'ondes et la fréquence angulaire peuvent être lus directement à partir de l'équation d'onde :

\ begin {align*}
y (x, t) =& A \ sin (k x-w t) =0,2 \ : \ mathrm {m} \ sin \ left (6,28 \ : \ mathrm {m} ^ {-1} x-1,57 \ : \ mathrm {s} ^ {-1} t \ right) \ nonnumber \ \
& \ left (A=0,2 \ : \ mathrm {m} ; k=6,28 \ : \ mathrm {m} ^ {-1} ; \ omega=1,57 \ : \ mathrm {s} ^ {-1} \ droite) \ nonumber
 \ end {align*}

2. Le numéro d'onde peut être utilisé pour trouver la longueur d'onde :

\ begin {tableau} {l}
k= \ frac {2 \ pi} {\ lambda} \ \
 \ lambda= \ frac {2 \ pi} {k} = \ frac {2 \ pi} {6,28 \ : \ mathrm {m} ^ {-1}} =1,0 \ : \ mathrm {m}
 \ end {tableau}

3. La période de l'onde peut être déterminée en utilisant la fréquence angulaire :

\ begin {tableau} {l}
 \ omega= \ frac {2 \ pi} {T} \ \
T= \ frac {2 \ pi} {\ omega} = \ frac {2 \ pi} {1,57 \ : \ mathrm {s} ^ {-1}} =4 \ : \ mathrm {s}
 \ end {tableau}

4. La vitesse de l'onde peut être déterminée à l'aide du nombre d'ondes et de la fréquence angulaire. La direction de l'onde peut être déterminée en considérant le signe de\(k x \mp \omega t\) : Un signe négatif suggère que l'onde se déplace dans la direction x positive :

\[ |v|=\frac{\omega}{k}=\frac{1.57 \: \mathrm{s}^{-1}}{6.28 \: \mathrm{m}^{-1}}=0.25 \: \mathrm{m} / \mathrm{s} \nonumber\]

L'importance

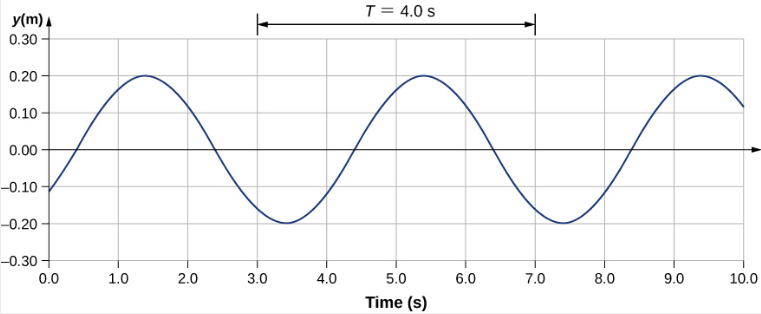
Toutes les caractéristiques de l'onde sont contenues dans la fonction d'onde. Notez que la vitesse de l'onde est la vitesse de l'onde dans la direction parallèle au mouvement de l'onde. Le fait de tracer la hauteur du milieu y par rapport à la position x pendant deux fois t = 0,00 s et t = 0,80 s peut fournir une visualisation graphique de l'onde (Figure\(\PageIndex{4}\)).

Figure\(\PageIndex{4}\) : Un graphique de la hauteur de la vague y en fonction de la position x pour des instantanés de la vague à deux moments. La ligne pointillée représente l'onde au temps t = 0,00 s et la ligne continue représente l'onde à t = 0,80 s. Comme la vitesse de l'onde est constante, la distance parcourue par l'onde est la vitesse de l'onde multipliée par l'intervalle de temps. Les points noirs indiquent les points utilisés pour mesurer le déplacement de l'onde. Le médium se déplace de haut en bas, tandis que la vague se déplace vers la droite.

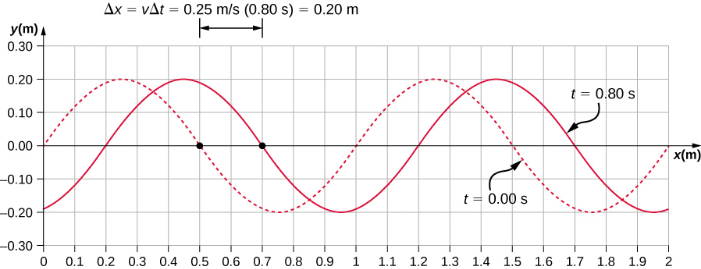
Le mouvement a une seconde vélocité. Dans cet exemple, l'onde est transversale et se déplace horizontalement lorsque le milieu oscille de haut en bas perpendiculairement à la direction du mouvement. Le graphique de la figure\(\PageIndex{5}\) montre le mouvement du milieu au point x = 0,60 m en fonction du temps. Notez que le milieu de la vague oscille de haut en bas entre y = +0,20 m et y = −0,20 m toutes les périodes de 4,0 secondes.

Figure\(\PageIndex{5}\) : Un graphique de la hauteur de la vague y en fonction du temps t pour la position x = 0,6 m. Le milieu oscille entre y = +0,20 m et y = −0,20 m à chaque période. La période représentée choisit deux points pratiques dans les oscillations pour mesurer la période. La période peut être mesurée entre deux points adjacents quelconques ayant la même amplitude et la même vitesse,\((\partial y / \partial t)\). La vitesse peut être déterminée en observant la pente tangente au point sur un diagramme y par rapport à t. Notez qu'aux instants t = 3,00 s et t = 7,00 s, les hauteurs et les vitesses sont les mêmes et la période d'oscillation est de 4,00 s.

Exercice\(\PageIndex{1}\)

La fonction d'onde ci-dessus est dérivée en utilisant une fonction sinusoïdale. Est-il possible d'utiliser une fonction cosinus à la place ?

Vitesse et accélération du milieu

Comme le montre l'exemple\(\PageIndex{2}\), la vitesse de l'onde est constante et représente la vitesse de l'onde lorsqu'elle se propage dans le milieu, et non la vitesse des particules qui le composent. Les particules du milieu oscillent autour d'une position d'équilibre lorsque l'onde se propage dans le milieu. Dans le cas de l'onde transversale se propageant dans la direction x, les particules oscillent de haut en bas dans la direction y, perpendiculairement au mouvement de l'onde. La vitesse des particules du milieu n'est pas constante, ce qui signifie qu'il y a accélération. La vitesse du milieu, qui est perpendiculaire à la vitesse de l'onde dans une onde transversale, peut être déterminée en prenant la dérivée partielle de l'équation de position par rapport au temps. La dérivée partielle est trouvée en prenant la dérivée de la fonction, en traitant toutes les variables comme des constantes, à l'exception de la variable en question. Dans le cas de la dérivée partielle par rapport au temps\(t\), la position\(x\) est traitée comme une constante. Bien que cela puisse paraître étrange si vous ne l'avez jamais vu auparavant, le but de cet exercice est de déterminer la vitesse transversale en un point, donc dans ce sens, la\(x\) position -ne change pas. Nous avons

\[\begin{split} y(x,t) & = A \sin (kx - \omega t + \phi) \\ v_{y} (x,t) & = \frac{\partial y(x,t)}{\partial t} = \frac{\partial}{\partial t} [A \sin (kx - \omega t + \phi)] \\ & = -A \omega \cos (kx - \omega t + \phi) \\ & = -v_{y\; max} \cos (kx - \omega t + \phi) \ldotp \end{split}\]

L'amplitude de la vitesse maximale du milieu est de\(|v_{y\, max}| = A \omega\). Cela peut sembler familier à cause des oscillations et d'une masse sur un ressort.

Nous pouvons déterminer l'accélération du milieu en prenant la dérivée partielle de l'équation de vitesse par rapport au temps,

\[\begin{split} a_{y} (x,t) & = \frac{\partial v_{y}(x,t)}{\partial t} = \frac{\partial}{\partial t} [-A \omega \cos (kx - \omega t + \phi)] \\ & = -A \omega^{2} \sin (kx - \omega t + \phi) \\ & = -a_{y\; max} \sin (kx - \omega t + \phi) \ldotp \end{split}\]

L'amplitude de l'accélération maximale est |a _{y max} | =\(\omega^{2}\) A. Les particules du milieu, ou les éléments de masse, oscillent selon un simple mouvement harmonique pour une onde mécanique.

L'équation d'onde linéaire

Nous venons de déterminer la vitesse du milieu à une position x en prenant la dérivée partielle, par rapport au temps, de la position y. Pour une onde transversale, cette vitesse est perpendiculaire à la direction de propagation de l'onde. Nous avons trouvé l'accélération en prenant la dérivée partielle, par rapport au temps, de la vitesse, qui est la deuxième dérivée temporelle de la position :

\[a_{y} (x,t) = \frac{\partial^{2} y(x,t)}{\partial t^{2}} = \frac{\partial^{2}}{\partial t^{2}} [A \sin(kx - \omega t + \phi)] = -A \omega^{2} \sin (kx - \omega t + \phi) \ldotp\]

Considérons maintenant les dérivées partielles par rapport à l'autre variable, la position x, en maintenant la constante de temps. La dérivée première est la pente de l'onde en un point x à un temps t,

\[slope = \frac{\partial y(x,t)}{\partial x} = \frac{\partial}{\partial x} [A \sin (kx - \omega t + \phi)] = Ak \cos (kx - \omega t + \phi) \ldotp\]

La deuxième dérivée partielle exprime la façon dont la pente de l'onde change par rapport à la position, en d'autres termes, la courbure de l'onde, où

\[curvature = \frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{\partial^{2}}{\partial x^{2}} [A \sin (kx - \omega t + \phi)] = -Ak^{2} \sin (kx - \omega t + \phi) \ldotp\]

Le rapport entre l'accélération et la courbure conduit à une relation très importante en physique connue sous le nom d'équation des ondes linéaires. En prenant le rapport et en utilisant l'équation v =, on\(\frac{\omega}{k}\) obtient l'équation d'onde linéaire (également appelée simplement équation d'onde ou équation d'une corde vibrante),

\[\begin{split} \frac{\frac{\partial^{2} y(x,t)}{\partial t^{2}}}{\frac{\partial^{2} y(x,t)}{\partial x^{2}}} & = \frac{-A \omega^{2} \sin (kx - \omega t + \phi)}{-Ak^{2} \sin (kx - \omega t + \phi)} \\ & = \frac{\omega^{2}}{k^{2}} = v^{2}, \end{split}\]

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp \label{16.6}\]

L'équation \ ref {16.6} est l'équation d'onde linéaire, qui est l'une des équations les plus importantes en physique et en ingénierie. Nous l'avons dérivé ici pour une onde transversale, mais il est tout aussi important lors de l'étude des ondes longitudinales. Cette relation a également été dérivée à l'aide d'une onde sinusoïdale, mais elle décrit avec succès toute onde ou impulsion de la forme y (x, t) = f (x vt). Ces ondes sont dues à une force de rappel linéaire du milieu, d'où le nom d'équation d'onde linéaire. Toute fonction d'onde qui satisfait à cette équation est une fonction d'onde linéaire.

Un aspect intéressant de l'équation d'onde linéaire est que si deux fonctions d'onde sont des solutions individuelles à l'équation d'onde linéaire, alors la somme des deux fonctions d'onde linéaires constitue également une solution à l'équation d'onde. Considérons deux ondes transversales qui se propagent le long de l'axe X et occupent le même milieu. Supposons que les ondes individuelles peuvent être modélisées avec les fonctions d'onde y ₁ (x, t) = f (x vt) et y ₂ (x, t) = g (x vt), qui sont des solutions aux équations d'ondes linéaires et sont donc des fonctions d'onde linéaires. La somme des fonctions d'onde est la fonction d'onde

\[y_{1} (x,t) + y_{2} (x,t) = f(x \mp vt) + g(x \mp vt) \ldotp\]

Considérez l'équation d'onde linéaire :

\[\begin{split} \frac{\partial^{2} (f + g)}{\partial x^{2}} & = \frac{1}{v^{2}} \frac{\partial^{2} (f + g)}{\partial t^{2}} \\ \frac{\partial^{2} f}{\partial x^{2}} + \frac{\partial^{2} g}{\partial x^{2}} & = \frac{1}{v^{2}} \left(\dfrac{\partial^{2} f}{\partial t^{2}} + \frac{\partial^{2} g}{\partial t^{2}}\right) \ldotp \end{split}\]

Cela a montré que si deux fonctions d'onde linéaires sont ajoutées de manière algébrique, la fonction d'onde résultante est également linéaire. Cette fonction d'onde modélise le déplacement du milieu de l'onde résultante à chaque position le long de l'axe X. Si deux ondes linéaires occupent le même milieu, on dit qu'elles interfèrent. Si ces ondes peuvent être modélisées à l'aide d'une fonction d'onde linéaire, ces fonctions d'onde s'ajoutent pour former l'équation d'onde de l'onde résultant de l'interférence des ondes individuelles. Le déplacement du milieu en tout point de l'onde résultante est la somme algébrique des déplacements dus aux ondes individuelles.

Pour aller plus loin dans cette analyse, si les fonctions d'onde y1 (x, t) = f (x vt) et y2 (x, t) = g (x vt) sont des solutions à l'équation d'onde linéaire, alors Ay ₁ (x, t) + By ₂ (x, y), où A et B sont des constantes, est également une solution à l'équation d'onde linéaire. Cette propriété est connue sous le nom de principe de superposition. L'interférence et la superposition sont traitées plus en détail dans Interférence des ondes.

Exemple\(\PageIndex{2}\): Interference of Waves on a String

Prenons l'exemple d'une très longue corde tendue par deux élèves, un à chaque extrémité. L'élève A fait osciller l'extrémité de la corde en produisant une onde modélisée avec la fonction d'onde y ₁ (x, t) = A sin (kx −\(\omega\) t) et l'étudiant B fait osciller la corde produisant deux fois la fréquence, en se déplaçant dans la direction opposée. Les deux vagues se déplacent à la même vitesse v =\(\frac{\omega}{k}\). Les deux ondes interfèrent pour former une onde résultante dont la fonction d'onde est y _R (x, t) = y ₁ (x, t) + y ₂ (x, t). Déterminez la vitesse de l'onde résultante à l'aide de l'équation d'onde linéaire\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\).

Stratégie

Tout d'abord, écrivez la fonction d'onde pour l'onde créée par le deuxième étudiant. Notez que la fréquence angulaire de la deuxième onde est le double de la fréquence de la première onde (2\(\omega\)), et comme la vitesse des deux ondes est la même, le nombre d'ondes de la deuxième onde est deux fois supérieur à celui de la première onde (2k). Ensuite, écrivez l'équation d'onde pour la fonction d'onde résultante, qui est la somme des deux fonctions d'onde individuelles. Trouvez ensuite la deuxième dérivée partielle par rapport à la position et la deuxième dérivée partielle par rapport au temps. Utilisez l'équation d'onde linéaire pour déterminer la vitesse de l'onde résultante.

Solution

1. Ecrivez la fonction d'onde de la deuxième vague : y ₂ (x, t) = A sin (2kx + 2\(\omega\) t).
2. Écrivez la fonction d'onde résultante : $$y_ {R} (x, t) = y_ {1} (x, t) + y (x, t) = A \ sin (kx - \ omega t) + A \ sin (2kx + 2 \ omega t) \ ldotp$$
3. Trouvez les dérivées partielles : $$ \ begin {split} \ frac {\ partial y_ {R} (x, t)} {\ partial x} & = -Ak \ cos (kx - \ omega t) + 2Ak \ cos (2kx + 2 \ omega t), \ \ \ frac {\ partial^ {2} y_ {R} (x, t)} {\ partial x^ {2}}} & = -Ak^ {2} \ sin (kx - \ oméga t) - 4Ak^ {2} \ sin (2kx + 2 \ oméga t), \ \ \ frac {\ partial y_ {R} (x, t)} {\ partiel t} & = -A \ oméga \ cos (kx - \ oméga t) + 2A \ oméga \ cos (2kx + 2 \ oméga t), \ \ \ frac {\ partial^ {2} y_ {R} (x, t)} {\ partial t^ {2}} & = -A \ omega^ {2} \ sin (kx - \ omega t) - 4A \ omega^ {2}} \ sin (2kx + 2 \ omega t) \ ldotp \ end {split} $$
4. Utilisez l'équation de l'onde pour déterminer la vitesse de l'onde résultante : $$ \ begin {split} \ frac {\ partial^ {2} y (x, t)} {\ partial x^ {2}} & = \ frac {1} {v^ {2}} \ frac {\ partial^ {2} y (x, t)} {\ partial t^ {2}}, \ \ -Ak^ {2} \ sin (kx - \ oméga t) + 4Ak^ {2} \ sin (2kx + 2 \ oméga t) & = \ frac {1} {v^ {2}} \ left (-A \ omega^ {2}} \ sin (kx - \ oméga t) - 4A \ oméga^ {2} \ sin (2kx + 2 \ oméga t) \ droite), \ \ k^ {2} \ gauche (-A \ sin (kx - \ omega t) + 4A \ sin (2kx + 2 \ oméga t) \ droite) & = \ frac {\ omega^ {2}} {v^ {2}} \ gauche (-A \ sin (kx - \ oméga t) - 4A \ sin (2kx + 2 \ oméga t) \ right), \ \ k^ {2} & = \ frac {\ omega^ {2}} {v^ {2}}, \ \ |v| & = \ frac {\ omega} {k} \ ldotp \ fin {split} $$

L'importance

La vitesse de l'onde résultante est égale à la vitesse des vagues d'origine\(\left(v = \frac{\omega}{k}\right)\). Nous montrerons dans la section suivante que la vitesse d'une simple onde harmonique sur une corde dépend de la tension de la corde et de la masse par longueur de la corde. Pour cette raison, il n'est pas surprenant que les ondes composantes et l'onde résultante se déplacent toutes à la même vitesse.

Exercice 16.4

L'équation d'onde\(\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}}\) fonctionne pour toute vague de la forme y (x, t) = f (x vt). Dans la section précédente, nous avons indiqué qu'une fonction cosinus pouvait également être utilisée pour modéliser une onde mécanique harmonique simple. Vérifiez si la vague

\[y(x,t) = (0.50\; m) \cos (0.20 \pi\; m^{-1} x - 4.00 \pi s^{-1} t + \frac{\pi}{10})\]

est une solution à l'équation des vagues.

Toute perturbation conforme à l'équation des vagues peut se propager sous la forme d'une onde se déplaçant le long de l'axe X avec une vitesse d'onde v. Elle fonctionne aussi bien pour les ondes sur une corde que pour les ondes sonores et les ondes électromagnétiques. Cette équation est extrêmement utile. Par exemple, il peut être utilisé pour montrer que les ondes électromagnétiques se déplacent à la vitesse de la lumière.