16.6 : Interférence des ondes

Objectifs d'apprentissage

• Expliquer comment les ondes mécaniques sont réfléchies et transmises aux limites d'un milieu
• Définissez les termes interférence et superposition
• Trouvez l'onde résultante de deux ondes sinusoïdales identiques qui ne diffèrent que par un décalage de phase

Jusqu'à présent, nous avons étudié les ondes mécaniques qui se propagent continuellement à travers un milieu, mais nous n'avons pas discuté de ce qui se passe lorsque des ondes rencontrent la limite du milieu ou de ce qui se passe lorsqu'une onde rencontre une autre onde se propageant à travers le même milieu. Les ondes interagissent avec les limites du milieu et peuvent être réfléchies en tout ou en partie. Par exemple, lorsque vous vous tenez à une certaine distance d'une falaise rigide et que vous criez, vous pouvez entendre les ondes sonores se refléter sur la surface rigide sous forme d'écho. Les ondes peuvent également interagir avec d'autres ondes se propageant dans le même milieu. Si vous jetez deux pierres dans un étang à une certaine distance l'une de l'autre, les ondulations circulaires produites par les deux pierres semblent se traverser au fur et à mesure qu'elles se propagent à partir de l'endroit où les pierres sont entrées dans l'eau. Ce phénomène est connu sous le nom d'interférence. Dans cette section, nous examinons ce qui arrive aux ondes qui rencontrent la limite d'un milieu ou à une autre onde se propageant dans le même milieu. Nous verrons que leur comportement est très différent de celui des particules et des corps rigides. Plus tard, lorsque nous étudierons la physique moderne, nous verrons que ce n'est qu'à l'échelle des atomes que nous voyons des similitudes dans les propriétés des ondes et des particules.

Réflexion et transmission

Lorsqu'une onde se propage à travers un milieu, elle se réfléchit lorsqu'elle rencontre la limite du milieu. La vague avant d'atteindre la limite est connue sous le nom d'onde incidente. L'onde après avoir rencontré la limite est connue sous le nom d'onde réfléchie. La façon dont l'onde est réfléchie à la limite du milieu dépend des conditions limites ; les ondes réagiront différemment si la limite du milieu est fixe ou libre de mouvement (Figure\(\PageIndex{1}\)). Une condition limite fixe existe lorsque le support situé à une limite est fixé en place de telle sorte qu'il ne peut pas se déplacer. Une condition de limite libre existe lorsque le milieu situé à la limite est libre de se déplacer.

Figure\(\PageIndex{1}\) : (a) Une extrémité d'une chaîne est fixée de telle sorte qu'elle ne peut pas bouger. Une onde se propageant sur la chaîne, rencontrant cette condition limite fixe, est réfléchie de 180° (\(\pi\)rad) hors phase par rapport à l'onde incidente. (b) Une extrémité d'une ficelle est attachée à un anneau solide de masse négligeable sur un mât de laboratoire sans friction, où l'anneau peut bouger librement. Une onde se propageant sur la chaîne, rencontrant cette condition de limite libre, est réfléchie en phase 0° (0 rad) par rapport à l'onde.

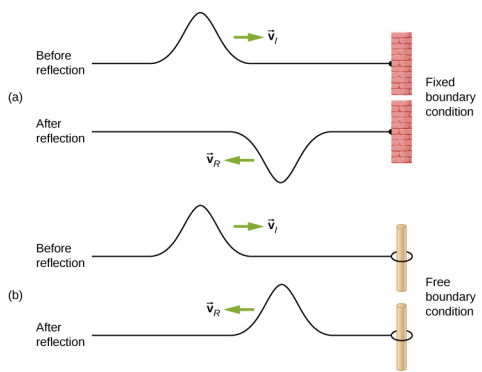
La figure\(\PageIndex{1a}\) montre une condition limite fixe. Ici, une extrémité de la corde est fixée à un mur, de sorte que l'extrémité de la ficelle est fixée en place et que le support (la corde) situé à la limite ne puisse pas bouger. Lorsque l'onde est réfléchie, l'amplitude de la voie réfléchie est exactement la même que l'amplitude de l'onde incidente, mais l'onde réfléchie est réfléchie (\(180^o \pi\)rad) hors phase par rapport à l'onde incidente. Le changement de phase peut être expliqué à l'aide de la troisième loi de Newton : rappelons que la troisième loi de Newton stipule que lorsque l'objet A exerce une force sur l'objet B, alors l'objet B exerce une force égale et opposée sur l'objet A. Lorsque l'onde incidente rencontre le mur, la corde exerce une force ascendante sur le mur et le mur réagit en exerçant une force égale et opposée sur la corde. La réflexion à une limite fixe est inversée. Notez que la figure montre une crête de l'onde incidente réfléchie sous la forme d'un creux. Si l'onde incidente était un creux, l'onde réfléchie serait une crête.

La figure\(\PageIndex{1b}\) montre une condition de limite libre. Ici, une extrémité de la corde est attachée à un anneau solide de masse négligeable sur un poteau sans friction, de sorte que l'extrémité de la corde peut se déplacer librement de haut en bas. Lorsque l'onde incidente rencontre la limite du milieu, elle est également réfléchie. Dans le cas d'une condition de limite libre, l'onde réfléchie est en phase par rapport à l'onde incidente. Dans ce cas, l'onde rencontre la limite libre en appliquant une force ascendante sur l'anneau, accélérant ainsi l'anneau vers le haut. L'anneau se déplace jusqu'à la hauteur maximale égale à l'amplitude de l'onde, puis accélère vers la position d'équilibre en raison de la tension de la corde. La figure montre la crête d'une onde incidente réfléchie en phase par rapport à l'onde incidente sous forme de crête. Si l'onde incidente était un creux, l'onde réfléchie serait également un creux. L'amplitude de l'onde réfléchie serait égale à l'amplitude de l'onde incidente.

Dans certaines situations, la limite du support n'est ni fixe ni libre. Considérez la figure\(\PageIndex{2a}\), où une chaîne à faible densité de masse linéaire est attachée à une chaîne de densité de masse linéaire plus élevée. Dans ce cas, l'onde réfléchie est déphasée par rapport à l'onde incidente. Il existe également une onde émise qui est en phase par rapport à l'onde incidente. Les ondes émises et réfléchies ont des amplitudes inférieures à l'amplitude de l'onde incidente. Si la tension est la même dans les deux cordes, la vitesse des vagues est plus élevée dans la corde dont la densité de masse linéaire est la plus faible.

Figure\(\PageIndex{2}\) : Ondes se déplaçant le long de deux types de cordes : une corde épaisse à haute densité linéaire et une corde fine à faible densité linéaire. Les deux cordes sont soumises à la même tension, de sorte qu'une onde se déplace plus rapidement sur la corde à faible densité que sur la corde à haute densité. (a) Une onde passant d'un milieu à faible vitesse à un milieu à grande vitesse produit une onde réfléchie déphasée de 180° (\(\pi\)rad) par rapport à l'impulsion (ou onde) incidente et une onde émise qui est en phase avec l'onde incidente. (b) Lorsqu'une onde passe d'un milieu à faible vitesse à un milieu à grande vitesse, l'onde réfléchie et l'onde émise sont toutes deux en phase par rapport à l'onde incidente.

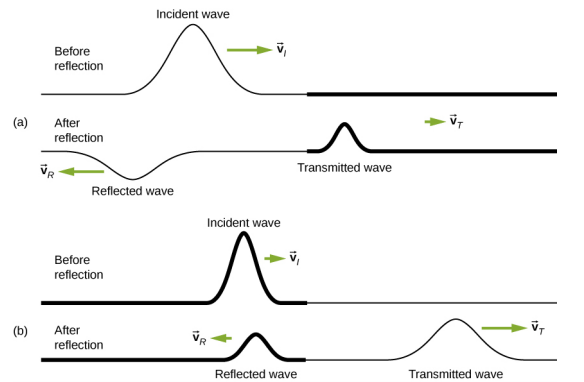
\(\PageIndex{2b}\)montre qu'une chaîne à haute densité de masse linéaire est attachée à une chaîne de densité linéaire inférieure. Dans ce cas, l'onde réfléchie est en phase par rapport à l'onde incidente. Il existe également une onde émise qui est en phase par rapport à l'onde incidente. Les ondes incidentes et réfléchies ont des amplitudes inférieures à l'amplitude de l'onde incidente. Vous remarquerez peut-être que si la tension est la même dans les deux cordes, la vitesse des vagues est plus élevée dans la corde ayant la densité de masse linéaire la plus faible.

Superposition et interférence

La plupart des vagues n'ont pas l'air très simples. Les vagues complexes sont plus intéressantes, voire plus belles, mais elles ont l'air formidables. Les ondes mécaniques les plus intéressantes consistent en une combinaison de deux ou plusieurs ondes progressives se propageant dans le même milieu. Le principe de superposition peut être utilisé pour analyser la combinaison d'ondes.

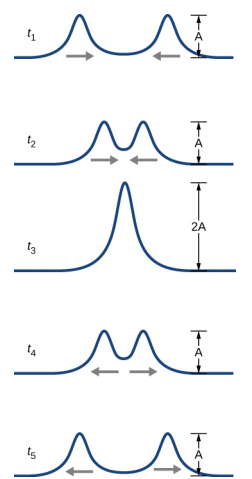
Considérez deux impulsions simples de même amplitude se déplaçant l'une vers l'autre dans le même milieu, comme le montre la figure\(\PageIndex{3}\). Finalement, les ondes se chevauchent, produisant une onde dont l'amplitude est deux fois supérieure, puis continuent sans être affectées par la rencontre. On dit que les impulsions interfèrent, et ce phénomène est connu sous le nom d'interférence.

Figure\(\PageIndex{3}\) : Deux impulsions se dirigeant l'une vers l'autre subissent des interférences. Le terme interférence fait référence à ce qui se produit lorsque deux ondes se chevauchent.

Pour analyser l'interférence de deux ou plusieurs ondes, nous utilisons le principe de superposition. Pour les ondes mécaniques, le principe de superposition stipule que si deux ou plusieurs ondes progressives se combinent au même point, la position résultante de l'élément de masse du milieu, à ce point, est la somme algébrique de la position due aux ondes individuelles. Cette propriété se manifeste par de nombreuses vagues observées, telles que des vagues sur une corde, des ondes sonores et des vagues d'eau de surface. Les ondes électromagnétiques obéissent également au principe de superposition, mais les champs électriques et magnétiques de l'onde combinée sont ajoutés au lieu du déplacement du milieu. Les ondes qui obéissent au principe de superposition sont des ondes linéaires ; les ondes qui n'obéissent pas au principe de superposition sont dites des ondes non linéaires. Dans ce chapitre, nous traitons des ondes linéaires, en particulier des ondes sinusoïdales.

Le principe de superposition peut être compris en considérant l'équation d'onde linéaire. Dans Mathematics of a Wave, nous avons défini une onde linéaire comme une onde dont la représentation mathématique obéit à l'équation d'onde linéaire. Pour une onde transversale sur une corde avec une force de rappel élastique, l'équation d'onde linéaire est

\[\frac{\partial^{2} y(x,t)}{\partial x^{2}} = \frac{1}{v^{2}} \frac{\partial^{2} y(x,t)}{\partial t^{2}} \ldotp\]

Toute fonction d'onde y (x, t) = y (x vt), où l'argument de la fonction est linéaire (x vt) est une solution à l'équation d'onde linéaire et est une fonction d'onde linéaire. Si les fonctions d'onde y ₁ (x, t) et y ₂ (x, t) sont des solutions à l'équation d'onde linéaire, la somme des deux fonctions y ₁ (x, t) + y ₂ (x, t) est également une solution de l'équation d'onde linéaire. Les ondes mécaniques qui obéissent à la superposition sont normalement limitées aux ondes dont l'amplitude est faible par rapport à leur longueur d'onde. Si l'amplitude est trop grande, le milieu est déformé au-delà de la zone où la force de rappel du milieu est linéaire.

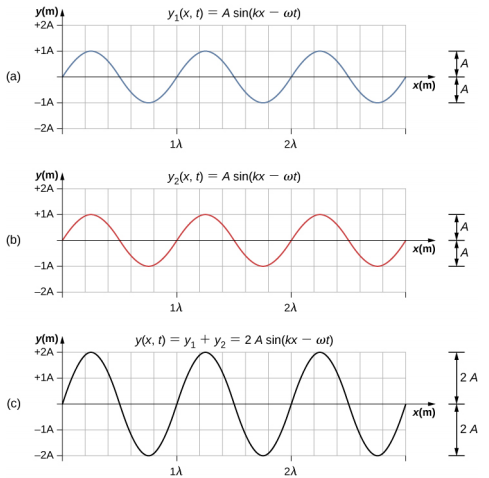
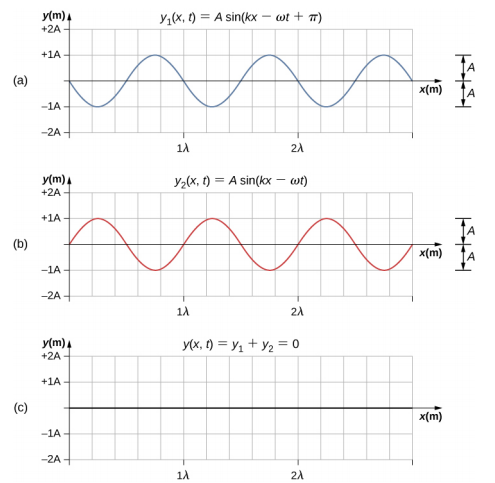
Les ondes peuvent interférer de manière constructive ou destructive. La figure\(\PageIndex{4}\) montre deux ondes sinusoïdales identiques qui arrivent au même point exactement en phase. Figure\(\PageIndex{4a}\) et\(\PageIndex{4b}\) montre les deux ondes individuelles. La figure\(\PageIndex{4c}\) montre l'onde résultante qui résulte de la somme algébrique des deux ondes linéaires. Les crêtes des deux vagues sont parfaitement alignées, tout comme les creux. Cette superposition produit des interférences constructives. Comme les perturbations s'ajoutent, les interférences constructives produisent une onde dont l'amplitude est deux fois supérieure à celle des ondes individuelles, mais qui a la même longueur d'onde.

Figure\(\PageIndex{4}\) : L'interférence constructive de deux ondes identiques produit une onde d'amplitude deux fois supérieure, mais de même longueur d'onde.

La figure\(\PageIndex{5}\) montre deux ondes identiques qui arrivent exactement à 180° hors phase, produisant des interférences destructrices. Figure\(\PageIndex{5a}\) et\(\PageIndex{5b}\) montre les ondes individuelles, et la figure\(\PageIndex{5c}\) montre la superposition des deux vagues. Comme les creux d'une onde ajoutent la crête de l'autre onde, l'amplitude résultante est nulle pour les interférences destructrices : les ondes s'annulent complètement.

Figure\(\PageIndex{5}\) : L'interférence destructrice de deux ondes identiques, dont l'une présente un déphasage de 180° (\(\pi\)rad), produit une amplitude nulle ou une annulation complète.

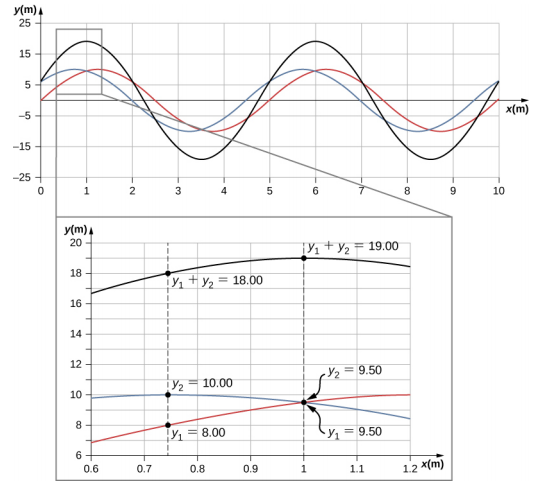
Lorsque des ondes linéaires interfèrent, l'onde résultante est simplement la somme algébrique des ondes individuelles, comme indiqué dans le principe de superposition. La figure\(\PageIndex{6}\) montre deux vagues (rouge et bleue) et l'onde résultante (noire). L'onde résultante est la somme algébrique des deux ondes individuelles.

Figure\(\PageIndex{6}\) : Lorsque deux ondes linéaires dans le même milieu interfèrent, la hauteur de l'onde résultante est la somme des hauteurs des ondes individuelles, prises point par point. Ce diagramme montre deux vagues (rouge et bleue) additionnées, ainsi que la vague résultante (noire). Ces graphiques représentent la hauteur de la vague à chaque point. Les ondes peuvent être n'importe quelle onde linéaire, y compris des ondulations sur un étang, des perturbations sur une corde, des sons ou des ondes électromagnétiques.

La superposition de la plupart des ondes produit une combinaison d'interférences constructives et destructives et peut varier d'un endroit à l'autre et d'une époque à l'autre. Le son d'une chaîne stéréo, par exemple, peut être fort à un endroit et faible à un autre. Une intensité variable signifie que les ondes sonores s'ajoutent de manière partiellement constructive et partiellement destructrice à différents endroits. Une chaîne stéréo possède au moins deux haut-parleurs qui créent des ondes sonores, et les ondes peuvent se refléter sur les murs. Toutes ces ondes interfèrent et l'onde qui en résulte est la superposition des ondes.

Nous avons montré plusieurs exemples de superposition d'ondes similaires. La figure\(\PageIndex{7}\) illustre un exemple de superposition de deux ondes différentes. Là encore, les perturbations s'additionnent, produisant une onde résultante.

Figure\(\PageIndex{7}\) : La superposition d'ondes non identiques présente des interférences à la fois constructives et destructives.

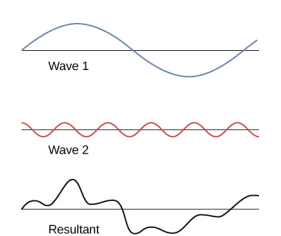
Parfois, lorsque deux ondes mécaniques ou plus interfèrent, le motif produit par l'onde résultante peut être riche en complexité, certains ne présentant aucun motif facilement discernable. Par exemple, tracer l'onde sonore de votre musique préférée peut sembler assez complexe. Il s'agit de la superposition des ondes sonores individuelles de nombreux instruments ; c'est la complexité qui rend la musique intéressante et vaut la peine d'être écoutée. À d'autres moments, les ondes peuvent interférer et produire des phénomènes intéressants, complexes dans leur apparence tout en étant beaux par la simplicité du principe physique de superposition qui a formé l'onde résultante. Un exemple est le phénomène connu sous le nom d'ondes stationnaires, produit par deux ondes identiques se déplaçant dans des directions différentes. Nous examinerons ce phénomène de plus près dans la section suivante.

Simulation

Essayez cette simulation pour créer des vagues à l'aide d'un robinet qui coule, d'un haut-parleur ou d'un laser ! Ajoutez une deuxième source ou une paire de fentes pour créer un modèle d'interférence. Vous pouvez observer une ou deux sources. À l'aide de deux sources, vous pouvez observer les modèles d'interférence résultant de la variation des fréquences et des amplitudes des sources.

Superposition d'ondes sinusoïdales qui diffèrent par un décalage de phase

De nombreux exemples en physique consistent en deux ondes sinusoïdales identiques en amplitude, en nombre d'ondes et en fréquence angulaire, mais qui diffèrent par un décalage de phase :

\[\begin{split} y_{1} (x,t) & = A \sin (kx - \omega t + \phi), \\ y_{2} (x,t) & = A \sin (kx - \omega t) \ldotp \end{split}\]

Lorsque ces deux ondes existent dans le même milieu, l'onde résultante résultant de la superposition des deux ondes individuelles est la somme des deux ondes individuelles :

\[y_{R} (x,t) = y_{1} (x,t) + y_{2} (x,t) = A \sin(kx - \omega t + \phi) + A \sin (kx - \omega t) \ldotp\]

L'onde résultante peut être mieux comprise en utilisant l'identité trigonométrique :

\[\sin u + \sin v = 2 \sin \left(\dfrac{u + v}{2}\right) \cos \left(\dfrac{u - v}{2}\right),\]

où u = kx -\(\omega\) t +\(\phi\) et v = kx -\(\omega\) t. L'onde résultante devient

\[\begin{split} y_{R} (x,t) & = y_{1} (x,t) + y_{2} (x,t) = A \sin (kx - \omega t + \phi) + A \sin (kx - \omega t) \\ & = 2A \sin \left(\dfrac{(kx - \omega t + \phi) + (kx - \omega t)}{2}\right) \cos \left(\dfrac{(kx - \omega t + \phi) - (kx - \omega t)}{2}\right) \\ & = 2A \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \cos \left(\dfrac{\phi}{2}\right) \ldotp \end{split}\]

Cette équation s'écrit généralement sous la forme

\[y_{R} (x,t) = 2A \cos \left(\dfrac{\phi}{2}\right) \sin \left(kx - \omega t + \dfrac{\phi}{2}\right) \ldotp \label{16.13}\]

L'onde résultante a le même nombre d'ondes et la même fréquence angulaire, une amplitude de A _R = [2A cos\(\left(\dfrac{\phi}{2}\right)\)] et un déphasage égal à la moitié du déphasage initial. Des exemples d'ondes qui ne diffèrent que par un décalage de phase sont présentés sur la figure\(\PageIndex{7}\).

Figure\(\PageIndex{8}\) : Superposition de deux ondes ayant des amplitudes, des longueurs d'onde et des fréquences identiques, mais dont le déphasage diffère. L'onde rouge est définie par la fonction d'onde y ₁ (x, t) = A sin (kx −\(\omega\) t) et l'onde bleue est définie par la fonction d'onde y ₂ (x, t) = A sin (kx −\(\omega\) t +\(\phi\)). La ligne noire indique le résultat de l'addition des deux vagues. La différence de phase entre les deux ondes est (a) 0,00 rad, (b)\(\frac{\pi}{2}\) rad, (c)\(\pi\) rad et (d)\(\frac{3 \pi}{2}\) rad.

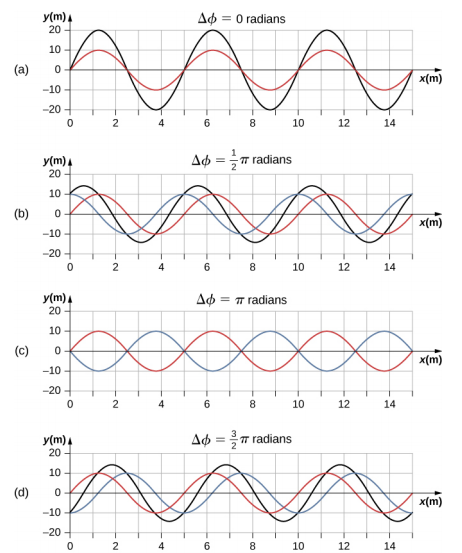
Les ondes rouges et bleues ont chacune la même amplitude, le même nombre d'ondes et la même fréquence angulaire, et ne diffèrent que par un décalage de phase. Ils ont donc la même période, la même longueur d'onde et la même fréquence. La vague verte est le résultat de la superposition des deux vagues. Lorsque les deux ondes ont une différence de phase nulle, les ondes sont en phase et l'onde résultante a le même nombre d'ondes et la même fréquence angulaire, et une amplitude égale au double des amplitudes individuelles (partie (a)). Il s'agit d'une ingérence constructive. Si la différence de phase est de 180°, les ondes interfèrent dans des interférences destructives (partie (c)). L'onde résultante a une amplitude nulle. Toute autre différence de phase produit une onde ayant le même nombre d'ondes et la même fréquence angulaire que les deux ondes incidentes, mais avec un déphasage\(\frac{\phi}{2}\) et une amplitude égales à 2A cos\(\left(\dfrac{\phi}{2}\right)\). Des exemples sont présentés dans les parties (b) et (d).